A - Leap Year
按照题意模拟即可。
B - Second Best
按照题意模拟即可。
C - Transportation Expenses
考虑当 \(x\) 增大时,\(\min(x, a_i) = x\) 的项会越来越少。换言之,当 \(x\) 足够大时,\(ans = \sum a_i\),若此时 \(ans > M\) 则说明无论补贴多少,这时答案都是一定的。
由于 \(x\) 越大花费一定越多,所以我们的花费是单调的,可以二分判断,复杂度 \(O(n \log n)\)。
D - AtCoder Janken 3
考虑条件:高桥从未输给过青木,这意味着每轮高桥的手势固定在平局和胜利的手势,于是我们可以有 \(f_{i, 0/1}\) 表示前 \(i\) 局,当前平/胜的最大胜场。
分类讨论上一步和当前步的手势即可。
E - Xor Sigma Problem
首先把式子里长度 \(\ge 2\) 的限制改为长度不限,然后把 \(ans - \sum a_i\) 即可。
然后再套路的把区间异或转化为前缀和。
因为我们发现不同位之间的贡献相互独立(因为异或是不进位加法),所以可以拆位计算每一位的贡献。
具体的,我们把所有 \(s_i\) 的第 \(i\) 位拆出来,如果当前为 \(1\),与 \(0\) 异或才有贡献,统计前面的 \(0\) 个数即可。\(0\) 同理。
复杂度 \(O(n \log V)\)。
F - Takahashi on Grid
思考实际上的过程,假设起点在左侧,终点在右侧。
过程一定形如:
- 当右侧不为墙时,移动到右侧。
- 否则,向上/下移动的第一个不为墙的位置。回到上一步。
因此,我们试着把移动过程中经过的区间分为两类:
- A 类,区间直上直下,不需要额外的上下移动。
- B 类,区间不能直上直下,需要额外的上下移动。
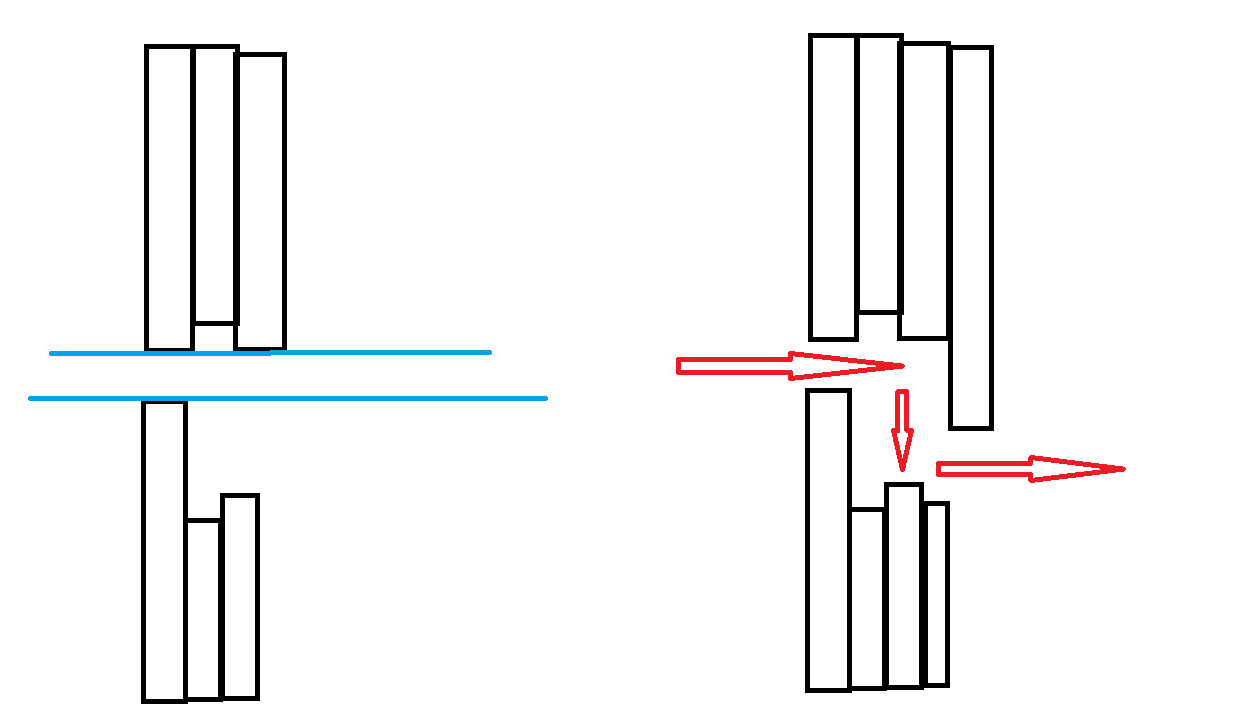
特殊说明,在这里我们只计算经过这些区间的纵向移动距离,因为横向移动距离实际上就是起终点的横坐标之差。
不难发现,经过 A 类需要的纵向移动距离为 \(0\)。
对于 B 类,我们发现这样的路线是存在一个 起点 和 终点 的,从目前坐标一定走到这条路径的起点,再走到终点是更优的。
此时 B 类的贡献即为起终点的纵坐标之差。
不难发现,我们的整体路线实际上就是若干个 AB 类路径拼接而成,而如果想询问 任意 区间的答案,不妨采用线段树维护。
具体的,对于两个区间,我们需要分类讨论以确定合并后的线段类型。
- 两个区间都为 A 类
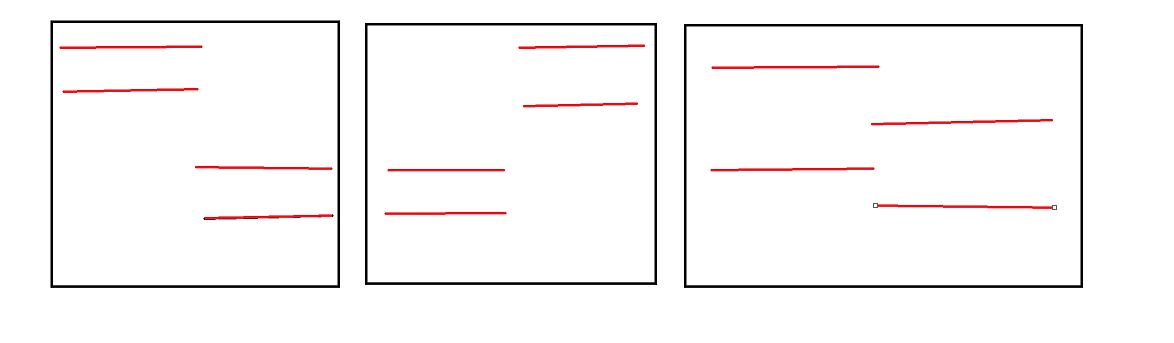
区间可以分为有交无交。
具体讨论合并
- 两个区间都为 B 类
G - AtCoder Office
如果用线段树维护,并把在的时间段设为 \(1\),那么询问相当于求线段树合并后满足和为 \(2\) 的段的长度,于是我们直接线段树合并即可。
但是考虑一种情况:当 A,B 所在段情况为
A:1 3 5 7 9 .. B: 2 4 6 8 10 ..
我们的线段树合并一定会递归到叶子,那么单次的复杂度就是 \(O(n \log n)\),总复杂度会达到 \(O(qn\log n)\)。
不过发现由于 \(m\) 是定值,那么均摊下来这样的段数一定不会太多,所以我们考虑记录先前询问过的答案,防止重复询问类似 A,B 一样的段,这样均摊下来就能过了。
均摊复杂度(也许):\((q\log n + n \log n)\)。
标签:AtCoder,code,log,题解,线段,移动,区间,365,复杂度 From: https://www.cnblogs.com/Rainsheep/p/18442330