题目看起来比较魔怔,考虑怎么搞一下。
首先,一个最简单的想法,每对溶液组都配一个板子,可以用 \(n^2\) 个板子解决,看得出来很不优啊,但是可以得到 Sub1 的分数。
节俭一点,我们如果把每个板子都拿出来一面用来对应一种溶液,此时就可以拼起来,只需要 \(2n\) 个板子解决,可以获得 Sub1,Sub2 的分数。
我们发现,上面的做法有一个很严重的缺陷:每个板子都有一面是没有接触过溶液的,我们考虑对这里进行优化。
考虑 \(X\) 没有接触过溶液的背面有什么用,我们把 \(X\) 平均分成两组,一组是 \(X_1 = \{x_1,x_2,\cdots,x_{\lfloor \frac{n}{2}\rfloor}\}\),一组是 \(X_2=\{x_{\lfloor \frac{n}{2}\rfloor+1},x_{\lfloor \frac{n}{2}\rfloor+2},\cdots,x_n\}\)。
我们现在为每个 \(X_1\) 的板子都和 \(Y\) 的分割板子去做实验,此时需要共 \(n+\lceil\frac{n}{2}\rceil\) 个
我们发现此时对于剩下的那一部分我们可以通过对板子进行组合来实现全部覆盖,那么总共需要的就是 \(\lceil\frac{n}{2}\rceil+ n\),通过计算我们可以发现正好多 \(1\),不能通过 Sub3。
因此我们需要对这个算法进行优化,发现其实我们对于奇数的情况完全不需要单独的一个板子,我们在完成翻转后的实验前,可以先让 \(x_n\) 和 \(Y\) 组实验,这样在最后可以减少一块额外的分隔板,因此可以优化到 \(\lfloor \frac{n}{2} \rfloor+n\),完全可以通过 Sub3。
考虑如何通过 Sub4,我们发现 Sub3 里用干净的板子去接触了不干净的板子导致干净的板子被污染了,如果能利用干净的板子就可以更优一点。
如果我们先把 \(X\) 和 \(Y\) 都平均分成三部分,然后先用 \(X_1\) 和 \(Y_{1\sim 3}\) 全部贴一次,此时我们会得到 \(\frac{n}{3} + n\) 个板子。

那么就会形成一个这样的图。

我们此时拿出 \(Y_3\) 翻转用没有染上的那面去染上灰色(灰色那里没有板子),此时我们在 \(Y_3\) 这里直接把 \(X_1\) 被污染的一面的和 \(Y_3\) 被污染的一面拼起来,此时就剩下没有被污染的两面,直接进行 \(X_2\) 与 \(Y\) 的配置即可。
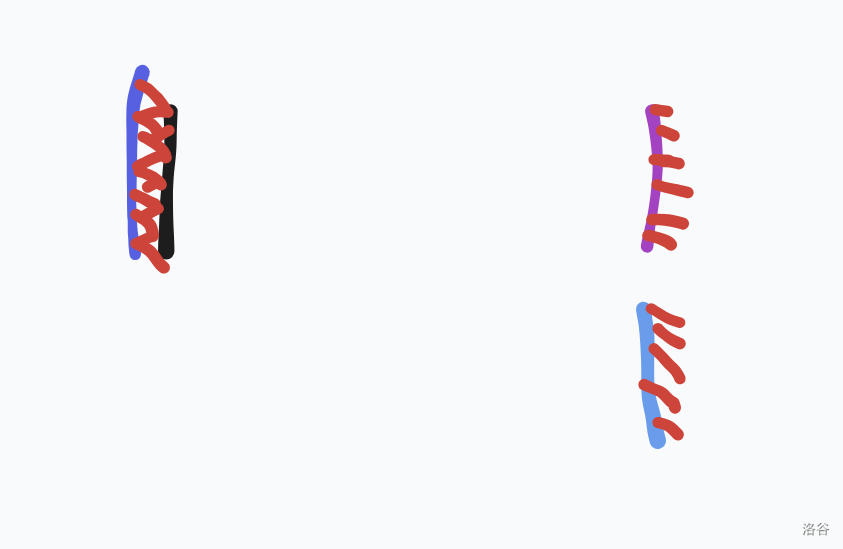
在染上之后我们的 \(X_1\) 两面都被污染了,但是容易发现 \(Y_1\) 和 \(Y_2\) 依然没有被污染。
我们直接把 \(Y_2\) 翻面给 \(X_3\),这样我们就能得到一个左侧 \(X_3\) 右侧 \(Y_2\) 的板子。
我们把原本有一面没被污染的 \(Y_1\) 和 \(Y_3\) 拼过来就行,需要 \(\frac{4n}{3}\) 个板子,能过 Sub4。
看一下 Sub5,我们发现 Sub4 有一些非常不优的地方导致了还可以进一步优化,可以发现在 Sub4 中我们的思路是保证那么一大片全都是空白的才能拼。
但是我们发现事实上我们只需要一个空白板即可。
我们对左边分成 \(4\) 份,对右边分成 \(4\) 份,此时只对于左边的 \(X_1\) 配板,对于右边全部配板。
然后把 \(X_1\) 与 \(Y_{\{1\sim 4\}}\) 全部反应一次,我们把 \(X_1\) 反过来放 \(X_2\),中间隔一个空白板,直接和 \(Y_{\{i\sim 4\}}\) 全部反应一次。
然后用类似上一步的方法进行反应即可,需要 \(\frac{n}{4}+n+1\) 块,可以通过 Sub5。
此时我们发现一件事,诶我们这里 \(X\) 和 \(Y\) 分的总量都是相同的,我们对于左侧分成两部分 \(X_1,X_2\),对于右侧分为三个部分 \(Y_1,Y_2,Y_3\),其中对于 \(X_1\) 配板,同时 \(Y_1,Y_2\) 配板。
我们先对于 \(X_1\) 和 \(Y_1,Y_2\) 进行实验,在试验后我们加入一个空白隔板,让 \(Y_1\) 翻面,此时隔着空白隔板进行 \(Y_3\) 的实验,空白隔板的一面会和 \(Y_1\) 接触导致污染。
此时我们翻转 \(X_1\) 进行 \(X_2\) 的实验,把空白隔板被污染的一面给到 \(X_1\) 被翻转的一面,然后进行实验 \(X_2\) 与 \(Y\) 的实验,由于 \(Y_2\) 还有一面没有被污染,所以刚好能行。
可通过 Sub7。
标签:frac,R3,P8477,板子,空白,污染,此时,GLR,我们 From: https://www.cnblogs.com/Vsinger-LuoTianYi/p/18441246