[介绍(百度百科)](笛卡尔树_百度百科 (baidu.com))
笛卡尔树是一种特定的二叉树数据结构,可由数列构造,在范围最值查询、范围\(top_k\)查询(range top k queries)等问题上有广泛应用。它具有堆的有序性,中序遍历可以输出原数列。笛卡尔树结构由Vuillmin(1980)在解决范围搜索的几何数据结构问题时提出。从数列中构造一棵笛卡尔树可以线性时间完成,需要采用基于栈的算法来找到在该数列中的所有最近小数。
特殊的\(treap\)
性质
先说性质感觉会更好理解一些
虽然是"树",但是笛卡尔树其实就是对序列的一个转化
对于树上的任意一点x,左右儿子left,right,以及在原序列上的\(pos\)值,有:
- 树中的元素满足二叉搜索树的性质,要求按照中序遍历得到的序列为原数组序列,各节点的\(pos\)是连续的,\(pos[left]<pos[x]<pos[right]\),(维持原序列的顺序)
- 树中节点满足堆性质,节点的\(val\)值要大于其左右子节点的\(val\)值,\(val[x]<val[left],val[right]\),(大根此时则恰恰相反)
对于笛卡尔树中每个节点都有两个权值\((val,key)\)
建树
可以使用线段树,st表这些数据结构维护区间最大值/最小值,但是没有必要,大多数笛卡尔树的题目都可以通过维护一个单调栈来实现\(O(n)\)的建树
- 使用单调栈维护最右链
- 每次插入当前的\(i\),在单调栈中不停弹出栈顶,直至栈顶\(fa\)满足\(val_{fa} < val_i\),则最后一次弹出的就是\(j\)
- 将\(i\)作为\(fa\)的右儿子,\(j\)作为\(i\)的左儿子
模拟一下就是:
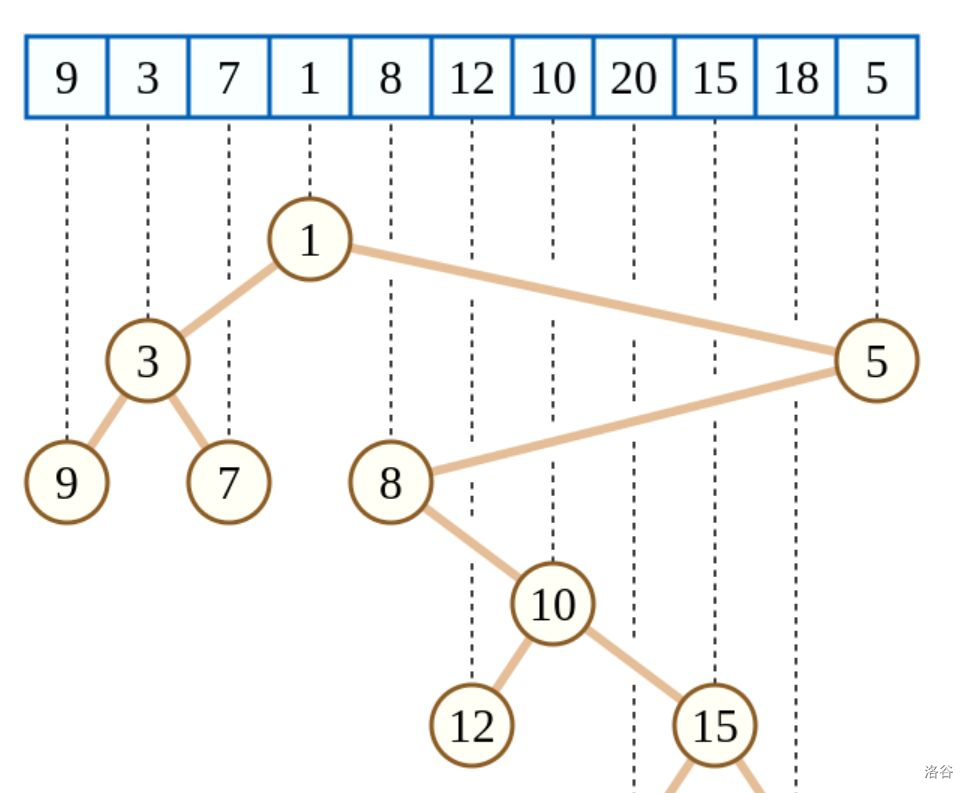
对于序列\(a=\{9,3,7,1,8,12,10,20,15,18,5\}\)
- 添加点\(1\),\(val_1=9\)加入栈
- 添加点\(2\),弹出点\(1\),点\(1\)就是\(fa\)的左儿子,将\(val_2=3\)加入栈,成为栈顶
- 添加点\(3\),\(val_3<val_2\),故成为点\(1\)的右儿子
- .................(见图)
[P5854 【模板】笛卡尔树](P5854 【模板】笛卡尔树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))
模板题,求建出树后就可以得到\(ans\)
#include"bits/stdc++.h"
using namespace std;
const int N=1e7+15;
#define inl inline
#define regi register
#define PII pair<int,int>
//#define ll long long
inl int read(void)
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) f=ch=='-'?-1:f,ch=getchar();
while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
return x*f;
}
int rt;int ls[N],rs[N],fa[N],n;
void build(int* a)
{
stack<int> sta;stack<int>().swap(sta);
for(int i=1;i<=n;i++)
{
int j=0;
while(!sta.empty()&&a[sta.top()]>a[i]) j=sta.top(),sta.pop();
if(sta.empty()) rt=i;
else rs[sta.top()]=i;
ls[i]=j;
sta.push(i);
}
}
int p[N],tot=0;
stack<int> sta;
void insert(int val)
{
p[++tot]=val;
int i=tot;
while(!sta.empty()&&p[sta.top()]>p[i]) sta.pop();
if(!sta.empty())
fa[i]=sta.top(),rs[sta.top()]=i,ls[i]=i-1;
else ls[i]=rt,rt=i;
sta.push(i);
}
struct RMQ
{
int L,R,dep[10015],sz[10015],ans;
int dfs1(int u)
{
dep[u]=dep[fa[u]]+1;
if(ls[u]) dfs1(ls[u]);
if(rs[u]) dfs1(rs[u]);
sz[u]+=sz[ls[u]],sz[u]+=sz[rs[u]];
}//lca(l,r)=min(val_l,val_r),dfs1->get_dep
RMQ(int l,int r):L(l),R(r){memset(dep,0,sizeof dep),memset(sz,0,sizeof sz);};
int get_RMQ(void)
{
int l=L,r=R;dfs1(1);
int u=l,v=r;
while(dep[u]!=dep[v])
{
if(dep[u]<dep[v]) swap(u,v);
u=fa[u];
}
ans=u;
}//log_2 n
};
int a[N];
int main(void)
{
n=read();
for(int i=1;i<=n;i++) a[i]=read();
build(a);
long long ans1=0,ans2=0;
for(int i=1;i<=n;i++) ans1^=1ll*i*(ls[i]+1),ans2^=1ll*i*(rs[i]+1);
printf("%lld %lld",ans1,ans2);
return 0;
}
[P4755 Beautiful Pair](P4755 Beautiful Pair - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))
有一个数列\({a}\),需要求出有多少数对\((i,j)\)满足\(a_i \times a_j \le \max_{l=i}^j{a_l}\)的数量
有很多人使用的都是线段树分治,但是提到笛卡尔树了,就写一下笛卡尔树分治
笛卡尔树在这些区间最值的地方有着非常不错的性质,考虑分治,区间为\([l,r]\),\(mid=(l+r)/2\),先转化一下式子为\(a_i\le \lfloor \frac{a_{mid}}{a_j} \rfloor\),笛卡尔树满足堆的性质,也满足搜索树的性质,套个\(cdq\)分治
建出笛卡尔树,可以很容易发现,贡献都是\(max\)两边提供的,考虑两边对答案的影响:
1.max的左子树的贡献
2.max的右子树的贡献
3.右边对左边的贡献
再维护一个树状数组
时间复杂度为\(O(n log^2 n)\)
#include"bits/stdc++.h"
using namespace std;
const int N=1e5+15,M=1e9+15;
#define inl inline
#define regi register
#define PII pair<int,int>
#define int long long
inl int read(void)
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) f=ch=='-'?-1:f,ch=getchar();
while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
return x*f;
}
int rt;
struct node
{
int ls,rs;
}tr[N];
int n;
void build(int* a)
{
stack<int> sta;stack<int>().swap(sta);
for(int i=1;i<=n;i++)
{
int j=0;
while(!sta.empty()&&a[sta.top()]<a[i]) j=sta.top(),sta.pop();
if(sta.empty()) rt=i;
else tr[sta.top()].rs=i;
tr[i].ls=j;
sta.push(i);
}
}
int ans;
int siz,a[N],b[N];
long long c[N];
#define lowbit(x) x&(-x)
void add(int x,int k){for(;x<=n;x+=lowbit(x))c[x]+=k;}
int query(int x){long long res=0;for(;x;x-=lowbit(x))res+=c[x];return res;}
void solve(int u,int l,int r)
{
if(u==0) return ;
int ls=tr[u].ls,rs=tr[u].rs;
int mid=u;
if(mid-l>r-mid)
{
for(int i=mid;i<=r;i++)
{
int x=upper_bound(b,b+siz+1,b[a[mid]]/b[a[i]])-b;
if(x) ans-=query(x-1);
}
solve(ls,l,mid-1),add(a[mid],1);
for(int i=mid;i<=r;i++)
{
int x=upper_bound(b,b+siz+1,b[a[mid]]/b[a[i]])-b;
if(x) ans+=query(x-1);
}
solve(rs,mid+1,r);
}
else
{
for(int i=l;i<=mid;i++)
{
int x=upper_bound(b,b+siz+1,b[a[mid]]/b[a[i]])-b;
if(x) ans-=query(x-1);
}
solve(rs,mid+1,r),add(a[mid],1);
for(int i=l;i<=mid;i++)
{
int x=upper_bound(b,b+siz+1,b[a[mid]]/b[a[i]])-b;
if(x) ans+=query(x-1);
}
solve(ls,l,mid-1);
}
}
signed main(void)
{
n=read();
for(int i=1;i<=n;i++) b[i]=a[i]=read();
sort(b+1,b+1+n);
siz=unique(b+1,b+1+n)-b-1;
for(int i=1;i<=n;i++) a[i]=lower_bound(b+1,b+1+siz,a[i])-b;
build(a);
solve(rt,1,n);
printf("%lld",ans);
return 0;
}