扫描线-学习笔记
引言:扫描线算法用于解决给出多个矩形组成的图形求解其面积、周长等问题。时间复杂度常见为 \(O(n\log_2^n)\) 级别,空间复杂度略大于 \(O(n)\) ,属于线段树的一种运用。
一、求面积
求 \(n\) 个四边平行于坐标轴的矩形的面积并。输入文件的第一行是一个整数 \(n\),然后输入 \(n\) 行,\(x1,y1,x2,y2\) ,表示一个矩形的四个端点坐标为 \((x1,y1),(x1,y2),(x2,y2),(x2,y1)\) 。
扫描线跟其名称一样,是一条线在坐标轴上自下而上扫过这个图形(也可以左右扫),每次经过的区域需要保持截面相同,见下图:
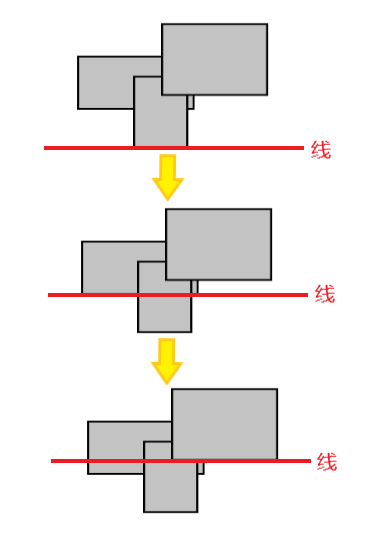
我们发现对于这个不规则图形其总面积为每次 \(经过高度\times相截长度\) 的总和,相当于把这个不规则图形的面积分成了数个规则矩形的面积和。
我们对于每个输入的矩形存储其的上下两条边,底边贡献为一,顶边贡献为负一(相当于加边和删边)。对所有的边按照纵坐标进行排序就是这条线需要经过的地方。
需要使用线段树维护相截长度,线段树所表示的区间是离散化过后的。对于一个节点维护两个值,分别是 \(Laz\)
和 \(sum\) ,表示这个区间被完全覆盖的次数和这个区间被覆盖的大小。
特别的,如果这个节点 \(Laz>0\) 那么其 \(sum\) 为区间大小。
\(Laz\) 不用向下传递。
代码如下:( \(X[i]\) 表示离散化后的 \(i\) 对应离散前的数值)
#include<bits/stdc .h>
#define int long long
using namespace std;
int read(){
int x=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=x*10 (ch-'0');
ch=getchar();
}
return x*w;
}
struct lin{
int l,r,h,mark; //边
}line[4000032];
bool cmp(const lin &x,const lin &y){
return x.h <y.h ;
}
int n,X[4000032];
struct node{
int Laz,sum,sl,sr;
}tree[4000032];
void build(int p,int l,int r){
tree[p].sl=l;
tree[p].sr=r;
tree[p].sum=tree[p].Laz=0;
if(l==r) return;
int mid=(l r)>>1;
build(p*2,l,mid);
build(p*2 1,mid 1,r);
}
void push_up(int p){
if(tree[p].Laz) tree[p].sum=X[tree[p].sr 1]-X[tree[p].sl];
else tree[p].sum=tree[p*2].sum tree[p*2 1].sum;
}
void add(int p,int L,int R,int w){
if(X[tree[p].sr 1]<=L||R<=X[tree[p].sl]) return;
if(L<=X[tree[p].sl]&&X[tree[p].sr 1]<=R){
tree[p].Laz =w;
push_up(p);
return;
}
int mid=(tree[p].sl tree[p].sr)>>1;
add(p*2,L,R,w);
add(p*2 1,L,R,w);
push_up(p);
}
signed main(){
n=read();
for(int i=1;i<=n;i ){
int x1,x2,y1,y2;
x1=read();y1=read();x2=read();y2=read();
X[i*2-1]=x1;
X[i*2]=x2;
line[i*2-1]=(lin){x1,x2,y1,1}; //存边
line[i*2]=(lin){x1,x2,y2,-1};
}
n<<=1;
sort(line 1,line n 1,cmp);
sort(X 1,X n 1); //离散化
int tot=unique(X 1,X n 1)-X-1; //求离散化后的数组大小
build(1,1,tot-1);
int ans=0;
for(int i=1;i<n;i ){
add(1,line[i].l,line[i].r,line[i].mark);
ans =tree[1].sum*(line[i 1].h-line[i].h);
}
cout<<ans<<endl;
return 0;
}
例题:P10096 扫地机器人
二、求周长
墙上贴着许多形状相同的照片。它们的边都是水平和垂直的。每个矩形图片可能部分或全部的覆盖了其他图片。所有矩形合并后的边长称为周长。输入文件的第一行是一个整数 \(N\) ,表示有多少个矩形。接下来 \(N\) 行给出了每一个矩形左下角坐标和右上角坐标。
求周长可以分成两个部分求解,纵边和横边。
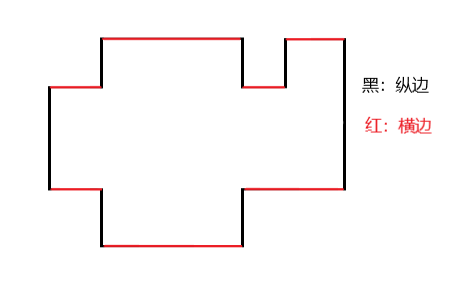
总周长为纵边长和横边长之和。
纵边长:
对于每次操作,纵边长为 \(线与图形相交不相连线段数\times高度差\times2\) 。如图,线1与图形相交不相连线段为 1 和 2,共两条。线2与图形相交不相连线段为 3 ,共一条。其实 \(线与图形相交不相连线段数\times2\) 就是纵边数量。
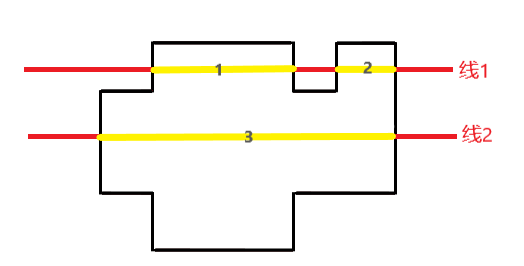
如何维护?
对于线段树上一个节点,再维护三个值,分别是 \((bool)lc\)、\((bool)rc\)、c 其中\(lc\) 和 \(rc\) 分别表示是否覆盖到区间左端、是否覆盖到区间右端, \(c\) 表示区间内线与图形相交不相连线段数。得到以下公式:
\(tree[p].c= \left\{ \begin{array}{lc} tree[lson].c+tree[rson].c-1& tree[lson].rc=1且tree[rson].lc=1 \\ tree[lson].c+tree[rson].c&other\\ \end{array} \right.\)
形象化的:
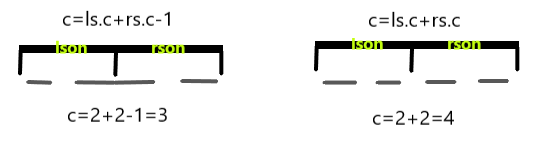
维护即可。
横边长:
对于每次操作,横边长为 \(\left| (上次相截长度-本次相截长度) \right|\) ,维护相截长度和上文相同方法。
注意:
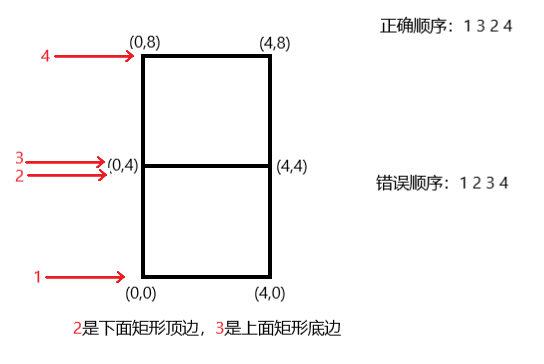
对于下图这种情况(边的高度相同)要先遍历底边再遍历顶边。
 )
)
正确顺序的 \(ans\) 和 \(tree[1].sum\) 变化
| 顺序 | tree[1].sum | ans |
|---|---|---|
| 1 | 4 | 12 |
| 3 | 4 | 12 |
| 2 | 4 | 20 |
| 4 | 0 | 24 |
错误顺序的 \(ans\) 和 \(tree[1].sum\) 变化
| 顺序 | tree[1].sum | ans |
|---|---|---|
| 1 | 4 | 12 |
| 2 | 0 | 16 |
| 3 | 4 | 28 |
| 4 | 0 | 32 |
原因:删边之后此位置还有边,但错误顺序以为此处无边。
代码如下:
#include<bits/stdc .h>
#define int long long
using namespace std;
int read(){
int x=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=x*10 (ch-'0');
ch=getchar();
}
return x*w;
}
struct lin{
int l,r,h,mark;
}line[4000032];
bool cmp(const lin &x,const lin &y){
if(x.h==y.h) return x.mark>y.mark;
return x.h <y.h ;
}
int n,X[4000032];
struct node{
int Laz,sum,sl,sr,c,lc,rc;
}tree[4000032];
void build(int p,int l,int r){
tree[p].sl=l;
tree[p].sr=r;
tree[p].sum=tree[p].Laz=0;
if(l==r) return;
int mid=(l r)>>1;
build(p*2,l,mid);
build(p*2 1,mid 1,r);
}
void push_up(int p){
if(tree[p].Laz){
tree[p].sum=X[tree[p].sr 1]-X[tree[p].sl];
tree[p].c=1;
tree[p].lc=tree[p].rc=1;
}else{
tree[p].sum=tree[p*2].sum tree[p*2 1].sum;
tree[p].c=tree[p*2].c tree[p*2 1].c;
if(tree[p*2].rc&&tree[p*2 1].lc) tree[p].c-=1;
tree[p].lc=tree[p*2].lc;
tree[p].rc=tree[p*2 1].rc;
}
}
void add(int p,int L,int R,int w){
if(X[tree[p].sr 1]<=L||R<=X[tree[p].sl]) return;
if(L<=X[tree[p].sl]&&X[tree[p].sr 1]<=R){
tree[p].Laz =w;
push_up(p);
return;
}
add(p*2,L,R,w);
add(p*2 1,L,R,w);
push_up(p);
}
signed main(){
n=read();
for(int i=1;i<=n;i ){
int x1,x2,y1,y2;
x1=read();y1=read();x2=read();y2=read();
X[i*2-1]=x1;
X[i*2]=x2;
line[i*2-1]=(lin){x1,x2,y1,1};
line[i*2]=(lin){x1,x2,y2,-1};
}
n<<=1;
sort(line 1,line n 1,cmp);
sort(X 1,X n 1); //离散化
int tot=unique(X 1,X n 1)-X-1; //求离散化后的数组大小
build(1,1,tot-1);
int ans=0,last=0;
for(int i=1;i<n;i ){
add(1,line[i].l,line[i].r,line[i].mark);
ans =abs(tree[1].sum-last);
ans =2*tree[1].c*(line[i 1].h-line[i].h);
last=tree[1].sum;
}
ans =line[n].r-line[n].l;
cout<<ans<<endl;
return 0;
}
\(------------------------------------\)
再附带上面求面积的例题代码:
#include<bits/stdc .h>
#define int long long
using namespace std;
int read(){
int x=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=x*10 (ch-'0');
ch=getchar();
}
return x*w;
}
struct lin{
int l,r,h,mark;
}line[4000032];
bool cmp(const lin &x,const lin &y){
return x.h <y.h ;
}
int n,X[4000032];
struct node{
int Laz,sum,sl,sr;
}tree[4000032];
void build(int p,int l,int r){
tree[p].sl=l;
tree[p].sr=r;
tree[p].sum=tree[p].Laz=0;
if(l==r) return;
int mid=(l r)>>1;
build(p*2,l,mid);
build(p*2 1,mid 1,r);
}
void push_up(int p){
if(tree[p].Laz) tree[p].sum=X[tree[p].sr 1]-X[tree[p].sl];
else tree[p].sum=tree[p*2].sum tree[p*2 1].sum;
}
void add(int p,int L,int R,int w){
if(X[tree[p].sr 1]<=L||R<=X[tree[p].sl]) return;
if(L<=X[tree[p].sl]&&X[tree[p].sr 1]<=R){
tree[p].Laz =w;
push_up(p);
return;
}
int mid=(tree[p].sl tree[p].sr)>>1;
add(p*2,L,R,w);
add(p*2 1,L,R,w);
push_up(p);
}
signed main(){
int k=read(),nx=0,ny=0;
n=read();
for(int i=1;i<=n;i ){
char opp[3];
scanf("%s",opp);char op=opp[0];
int x=read();
if(op=='N'){
X[i*2-1]=nx;
X[i*2]=nx k;
line[i*2-1]=(lin){nx,nx k,ny,1};
line[i*2]=(lin){nx,nx k,ny x k,-1};
ny =x;
}else if(op=='E'){
X[i*2-1]=nx;
X[i*2]=nx x k;
line[i*2-1]=(lin){nx,nx x k,ny,1};
line[i*2]=(lin){nx,nx x k,ny k,-1};
nx =x;
}else if(op=='W'){
X[i*2-1]=nx k;
X[i*2]=nx-x;
line[i*2-1]=(lin){nx-x,nx k,ny,1};
line[i*2]=(lin){nx-x,nx k,ny k,-1};
nx-=x;
}else{
X[i*2-1]=nx;
X[i*2]=nx k;
line[i*2-1]=(lin){nx,nx k,ny-x,1};
line[i*2]=(lin){nx,nx k,ny k,-1};
ny-=x;
}
}
n<<=1;
sort(line 1,line n 1,cmp);
sort(X 1,X n 1);
int tot=unique(X 1,X n 1)-X-1;
build(1,1,tot-1);
int ans=0;
for(int i=1;i<n;i ){
add(1,line[i].l,line[i].r,line[i].mark);
ans =tree[1].sum*(line[i 1].h-line[i].h);
}
cout<<ans;
return 0;
}
感谢阅读orz
标签:ch,lc,int,sum,tree,笔记,学习,扫描线,矩形 From: https://www.cnblogs.com/woxitao/p/18440529