机器人搬重物
题目描述
机器人移动学会(RMI)现在正尝试用机器人搬运物品。机器人的形状是一个直径 \(1.6\) 米的球。在试验阶段,机器人被用于在一个储藏室中搬运货物。储藏室是一个 \(N\times M\) 的网格,有些格子为不可移动的障碍。机器人的中心总是在格点上,当然,机器人必须在最短的时间内把物品搬运到指定的地方。机器人接受的指令有:
- 向前移动 \(1\) 步(
Creep); - 向前移动 \(2\) 步(
Walk); - 向前移动 \(3\) 步(
Run); - 向左转(
Left); - 向右转(
Right)。
每个指令所需要的时间为 \(1\) 秒。请你计算一下机器人完成任务所需的最少时间。
输入格式
第一行为两个正整数 \(N,M\ (1\le N,M\le50)\),下面 \(N\) 行是储藏室的构造,\(0\) 表示无障碍,\(1\) 表示有障碍,数字之间用一个空格隔开。接着一行有 \(4\) 个整数和 \(1\) 个大写字母,分别为起始点和目标点左上角网格的行与列,起始时的面对方向(东 \(\tt E\),南 \(\tt S\),西 \(\tt W\),北 \(\tt N\)),数与数,数与字母之间均用一个空格隔开。终点的面向方向是任意的。
输出格式
一个整数,表示机器人完成任务所需的最少时间。如果无法到达,输出 \(-1\)。
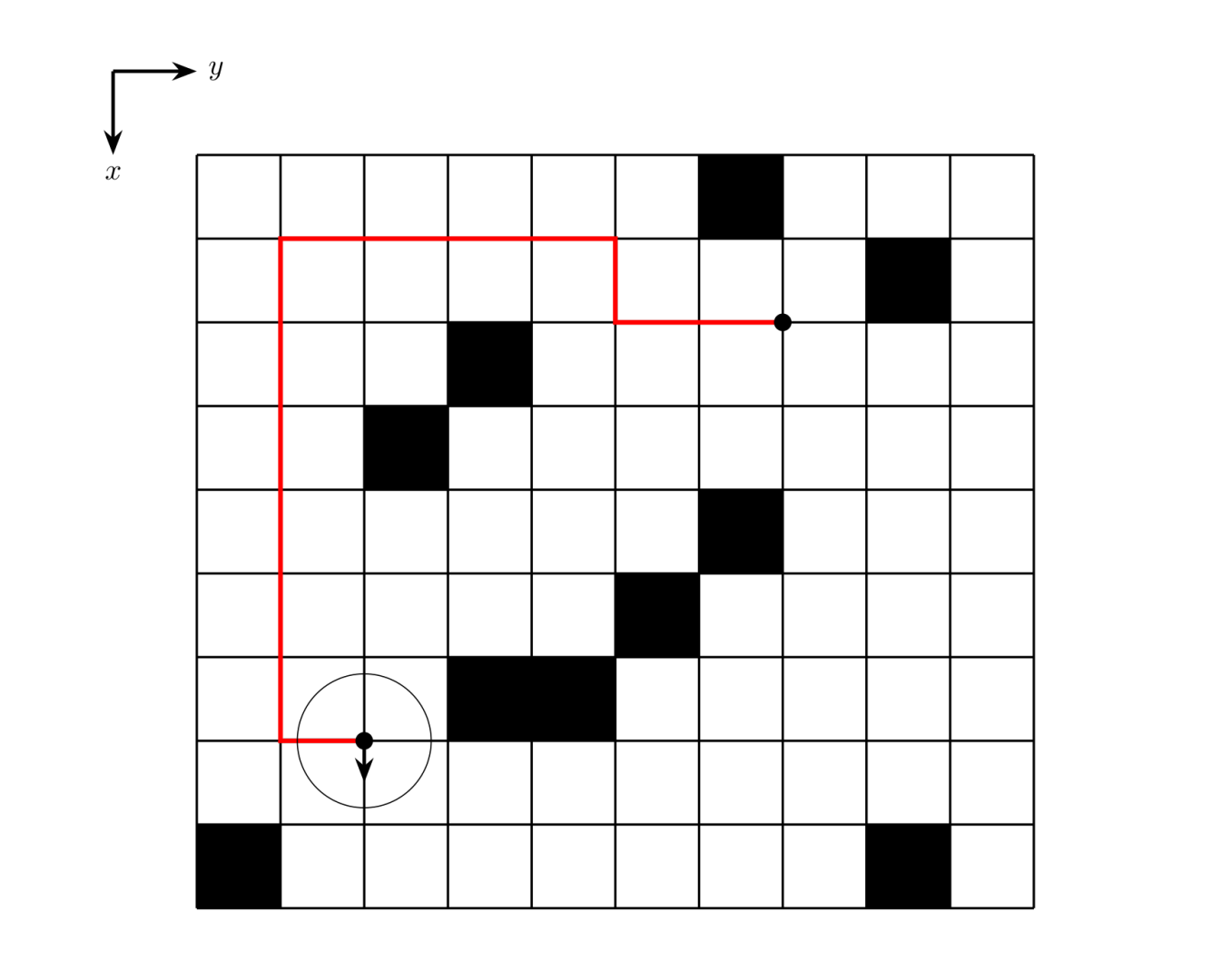
样例 #1
样例输入 #1
9 10
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0 0 0
0 0 0 1 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 1 0
7 2 2 7 S
样例输出 #1
12
本题是一个很典型的dfs题,但坑点很多,一连坑了我好多次。。。。不嘻嘻
- 首先就是计算转向的时间,我将NSWE是个方向代数为1,2,3,4,然后取他们差的绝对值,代表转向的时间,但是没有注意到4和1相差3,但实际上只用1秒,这个错纯属犯病。。。写太快了.
- 然后就是如何将输入的方格图转化为格点图,这个要画出图来

- 之后就是机器人走三步的时候有可能跳过障碍,但这是不允许的,所以需要剪枝
- 最后就是要用优先队列优先取出tm最小的节点
- 还有就是它测试用例的一些毒点,比如起点卡墙里(@-@!
具体细节在代码里
代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<queue>
#include<cmath>
#include<iomanip>
using namespace std;
int a[55][55]; //存储方格图
long long mp[55][55]; //存储格点图,即机器人行走的图
int dis[55][55]; //用于记录机器人到该格点的最短时间
int n, m; //方格图的尺寸
int x1, y11, x2, y2; //记录起点终点坐标
int sto;//起点的方向
string ch;//读入起点的方向
struct node
{
int x;
int y;//当前点的坐标
int to;//1=>N(上) 2=>E(右) 3=>S(下) 4=>W(左) 方向编号
int tm;//从起点到当前点的最短时间
bool operator < (node a)const {
return tm > a.tm;
}
//stl中优先队列默认优先取出最大值,所以要重载运算符,保证每次取出的都是代价最小的元素
};
priority_queue<node> que;//优先队列
node now, nxt;
int dx[] = { 0, -1,0,1,0 };
int dy[] = { 0, 0,1,0,-1 };
int abs(int a, int b) {
return a > b ? a - b : b - a;
}
int calchange(int now, int aft) {
//注意这个情况
if (abs(now, aft) == 3) {
return 1;
}
else {
return abs(now, aft);
}
}
void readto()
{
switch (ch[0])
{
case 'N': sto = 1; break;
case 'S': sto = 3; break;
case 'W': sto = 4; break;
case 'E': sto = 2; break;
}
return;
}
void change()
{
//把边框全部置为1,因为机器人有宽度,不能出现在那里
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= m; ++j)
{
if (a[i][j] == 1)//如果当前格为障碍物,则它的四个顶点都不能走
{
mp[i + 1][j] = 1;
mp[i][j + 1] = 1;
mp[i + 1][j + 1] = 1;
mp[i][j] = 1;
}
if (i == 1 || j == 1) {
mp[i][j] = 1;
}
if (i == n || j == m) {
mp[i + 1][j + 1] = 1;
}
}
}
mp[n + 1][1] = 1;
mp[1][m + 1] = 1;
}
void bfs() {
dis[x1+1][y11+1] = 0;
node fir;
fir.x = x1+1;
fir.y = y11+1;
fir.to = sto;
fir.tm = 0;
que.push(fir);
int changecost = 0;
while (!que.empty()) {
now = que.top();
//这个是打印路径的代码
//cout << now.x << " " << now.y << " " << now.to << " " << now.tm << endl;
if (now.x == x2+1 && now.y == y2+1) break; //剪枝
que.pop();
if (now.tm > dis[now.x][now.y]) continue; //剪枝,这个可不加,好像没用
//遍历四个方向
for (int i = 1; i <= 4; i++) {
changecost = calchange(now.to, i);
//三种移动方式
for (int j = 1; j <= 3; j++) {
nxt.x = now.x + dx[i] * j;
nxt.y = now.y + dy[i] * j;
//if (mp[nxt.x][nxt.y] == 1 && j==1 || mp[nxt.x][nxt.y] == 1 && j == 2) break;
if (nxt.x <= 1 || nxt.x > n || nxt.y <= 1 || nxt.y > m || mp[nxt.x][nxt.y] == 1) break; //剪枝,这个边界判断最好对着图来
nxt.to = i;
nxt.tm = now.tm + 1 + changecost;
if (dis[nxt.x][nxt.y] > nxt.tm) {
dis[nxt.x][nxt.y] = nxt.tm;
que.push(nxt);
}
}
}
}
}
int main()
{
memset(dis, 1061109567, sizeof(dis));
cin >> n >> m;
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= m; ++j)
{
scanf("%d", &a[i][j]);
}
}
cin >> x1 >> y11 >> x2 >> y2; //在c++中y1是个函数,所以要换一个
cin >> ch;
readto();//判断ch代表的方向
change();//把方格地图转化为机器人可以走的格点地图
//特判一下,防止依赖就卡墙,或者终点卡墙,这个起点和终点的索引最好对着图来
if (mp[x1 + 1][y11 + 1] == 1 || mp[x2+1][y2+1]==1) {
cout << -1;
return 0;
}
bfs();
//这个是打印格点图的代码,可以打印出来看看
/*for (int i = 1; i <= n + 1; i++) {
for (int j = 1; j <= m + 1; j++) {
cout << mp[i][j] << " ";
}
cout << endl;
}*/
if (dis[x2+1][y2+1] == 1061109567) {
cout << -1;
}
else {
cout << dis[x2 + 1][y2 + 1];
}
}