[神经网络与深度学习笔记]PCA降维

PCA降维

PCA是一种无监督降维算法，它是最常用的降维算法之一，可以很好的解决因变量太多而复杂性，计算量增大的弊端。

本质上讲，PCA就是将高维的数据通过线性变换投影的方式映射到低维空间上去，并且保证在投影的维度上，原数据的信息量最大（损失最小）。

PCA的具体步骤

• 1.特征中心化。每一维的数据都减去该维的均值。这里的“维”指的就是一个特征（或属性），变换之后每一维的均值都变成了0。每一列减去该列均值后，得到矩阵B

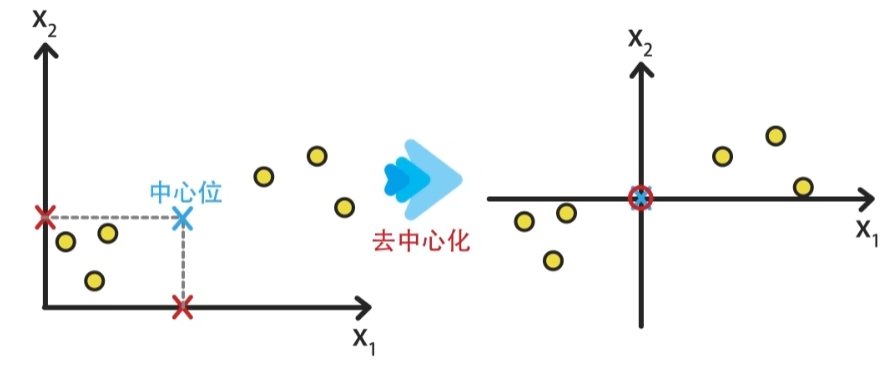
去中心化不会影响样本的分布性质，可以简化PCA算法的推倒过程

• 计算B的协方差矩阵C
• 求出协方差矩阵C的特征值和对应的特征向量
• 从大到小排序特征值，取得最前的k个特征向量P
• 将数据转换到k个特征向量构建的新空间中

import matplotlib
import numpy as np
from sklearn.decomposition import PCA
from sklearn.datasets import fetch_olivetti_faces
import matplotlib.pyplot as plt
import cv2

matplotlib.use('TkAgg')  # 指定交互式框架为TkAgg
# 加载人脸数据集
faces = fetch_olivetti_faces()
pic_seed = 10
X = faces.data

# 随机选择一张人脸图片
face = X[pic_seed].reshape(64, 64)

# 将人脸数据进行PCA降维
# 将数据降维到50个主成分
# n_components = [50]
n_components = [50,40,30,20,10]
# 显示结果
fig, axs = plt.subplots(1, len(n_components)+1, figsize=(10, 10))
axs[0].imshow(face, cmap='gray')
axs[0].set_title('Original Face')
index = 1

for items in n_components:
    pca = PCA(n_components=items)
    X_pca = pca.fit_transform(X)

    # 将降维后的数据进行逆转换
    X_restored = pca.inverse_transform(X_pca)

    face_restored = X_restored[pic_seed].reshape(64, 64)

    axs[index].imshow(face_restored, cmap='gray')
    axs[index].set_title(str(items))
    index += 1

plt.show()

左一为原始的64*64图像，通过pca降维成50、40、30、20、10个维度之后

通过逆转换还原图像得到结果

还有一个是葡萄酒数据集

# 读取数据（）
df_wine = pd.read_csv('wine.data',header=None)
# 设置列索引
df_wine.columns =  ['Class label', 'Alcohol', 'Malic acid', 'Ash',
                   'Alcalinity of ash', 'Magnesium', 'Total phenols',
                   'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins',
                   'Color intensity', 'Hue',
                   'OD280/OD315 of diluted wines', 'Proline']

数据维度为178*14

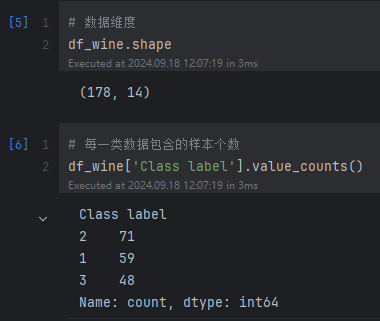
该数据集是UCI的公开数据集，是对意大利同一地区种植的葡萄酒进行分析的结果，数据集共14列数据，第一个属性是类标识符，分别是1/2/3来表示，代表葡萄酒的三个分类。剩余的13个属性是，酒精、苹果酸、灰、灰分的碱度、镁、总酚、黄酮类化合物、非黄烷类酚类、原花色素、颜色强度、色调等。

数据集划分

# 数据集设置：X为样本特征数据，y为目标数据，即标注结果
X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values

# 数据集划分： 将数据集划分为训练集和测试集数据（测试集数据为30%，训练集为70%）
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,
                                                    stratify=y,
                                                    random_state=0)

数据标准化

# 实例化
sc = StandardScaler()

# 对数据集进行标准化（一般情况下我们在训练集中进行均值和方差的计算，直接在测试集中使用）
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.transform(X_test)

PCA实现

# 计算协方差矩阵
cov_mat = np.cov(X_train_std.T)

# 对协方差矩阵进行特征值分解
eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)

得到特征值

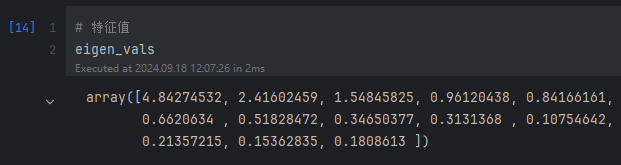
特征值分布

# 特征值之和
tot = sum(eigen_vals)

# 对特征进行排序，并计算所占的比例
var_exp = [(i / tot) for i in sorted(eigen_vals, reverse=True)]

# 累计求和
cum_var_exp = np.cumsum(var_exp)

# 绘制图像
plt.figure()
plt.bar(range(1, 14), var_exp, alpha=0.5, align='center',
        label='特征值分布')
plt.step(range(1, 14), cum_var_exp, where='mid',
         label='累计特征值')
plt.ylabel('特征值比例')
plt.xlabel('特征index')
plt.legend(loc='best')

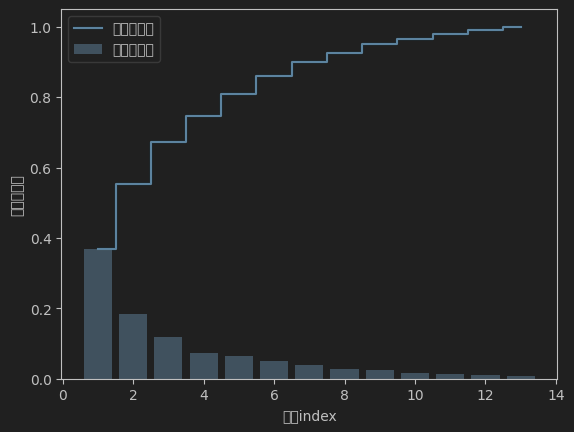
特征降维

# 创建列表，由(eigenvalue, eigenvector)元组构成
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i])
               for i in range(len(eigen_vals))]
               
# 按特征值从大到小对列表(eigenvalue, eigenvector)排序
eigen_pairs.sort(key=lambda k: k[0], reverse=True)

# 取前两个特征值对应的特征向量作为主要成分
w = np.hstack((eigen_pairs[0][1][:, np.newaxis],
               eigen_pairs[1][1][:, np.newaxis]))

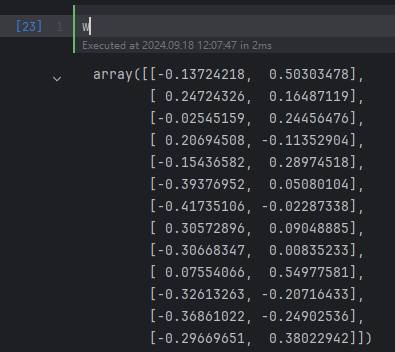
进行特征压缩

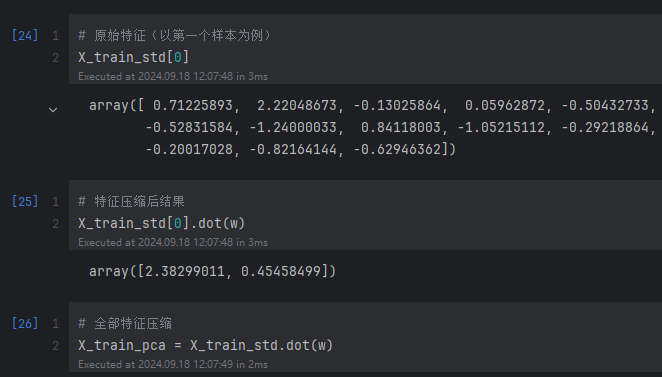
结果展示

# 特征压缩后结果展示
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']

for l, c, m in zip(np.unique(y_train), colors, markers):
    # 按照样本的真实值进行展示
    plt.scatter(X_train_pca[y_train == l, 0], 
                X_train_pca[y_train == l, 1], 
                c=c, label=l, marker=m)

plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()

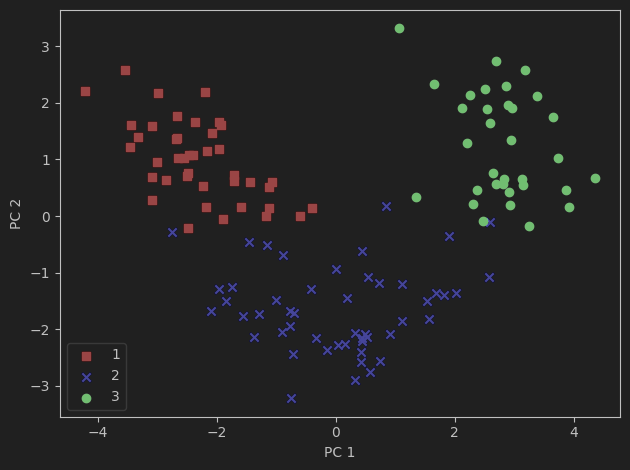
这个结果有助于之后进行分类