标签：ps p1 Point 马踏 棋盘 算法 curPoint 位置 day53

马踏棋盘

1.算法优化的意义

1. 算法是程序的灵魂，为什么有些程序可以在海量数据计算时，依旧保持高速计算？
2. 编程中算法很多，比如八大排序算法（冒泡、选择、插入、快排、归并、希尔、基数、堆排序）、查找算法、分治算法、动态规划算法、KMP算法、贪心算法、普利姆算法、克鲁斯卡尔算法、迪杰斯特拉算法、弗洛伊德算法
3. 下面以骑士周游问题为例，体验算法优化程序的意义，感受算法的威力

2.骑士周游问题

• 马踏棋盘算法介绍和游戏演示

1. 马踏棋盘算法也被称为骑士周游问题
2. 将马随机放在国际象棋的8*8棋盘Board[0-7][0-7]的某个方格中，马按走棋规则移动（马只能走日字）。要求每个方格只进入一次，走遍棋盘上全部64个方格
3. 会使用到图的遍历算法（DFS）+贪心算法优化

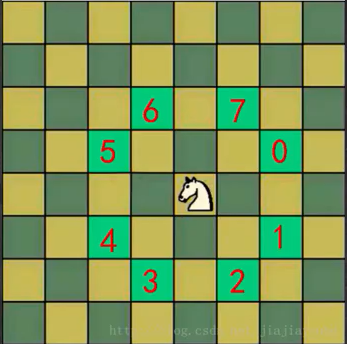
马踏棋盘(骑士周游问题)实际上是图的深度优先搜索(DFS)的应用。

使用回溯(就是深度优先搜索)来解决，假如马儿踏了53个点，如图，走到了第53个，坐标为(1,0)，发现已经走到了尽头，没办法，那就只能回退了，查看其它的路径，就在棋盘上不停地回溯……

这里我们先用基本的方法解决，然后使用贪心算法(greedyalgorithm)进行优化。解决马踏棋盘问题，体会到不同的算法对程序效率的影响

3.思路分析

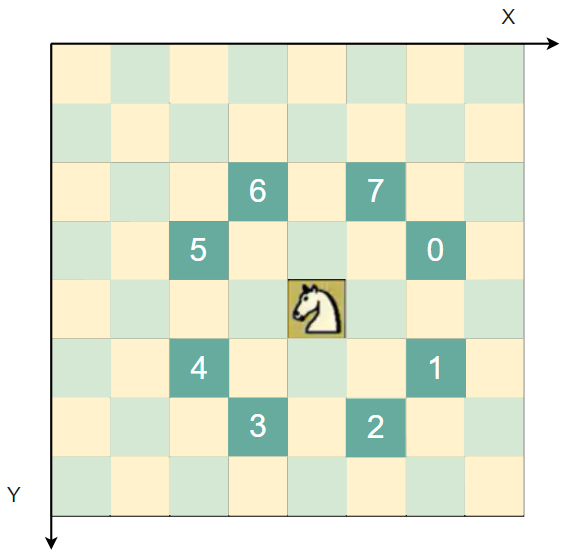
1. 创建一个棋盘chessBoard，是一个二维数组
2. 将马儿当前位置设置为已经访问，然后根据当前位置，计算马儿还能走哪些位置，并放入到一个集合中(ArrayList)，每一个位置的下一步最多有8个方向，每走一步，就使用step+1
3. 遍历ArrayList中存放的所有位置，看看哪个可以走，如果可以走通，就继续，走不通，就回溯
4. 判断马儿是否完成了任务，使用step和应该走的步数比较，如果没有达到数量，则表示没有完成任务，将整个棋盘设置为0

注意：马儿走的策略不同，得到的结果也会不一样，效率也不一样。

package li;

import java.awt.*;
import java.util.ArrayList;

/**
 * @author 李
 * @version 1.0
 * 马踏棋盘
 */
public class HorseChessBoard {
    //定义属性
    private static int X = 6;//表示col-列
    private static int Y = 6;//表示row-行
    private static int[][] chessBoard = new int[Y][X];//棋盘
    private static boolean[] visited = new boolean[X * Y];//表示记录某个位置是否走过
    private static boolean finished = false;//记录马儿是否遍历完棋盘

    public static void main(String[] args) {
        //测试
        int row = 2;
        int col = 2;
        long start = System.currentTimeMillis();
        traversalChessBoard(chessBoard, row-1, col-1, 1);//将棋盘上开始的位置设置为起始第一步
        long end = System.currentTimeMillis();
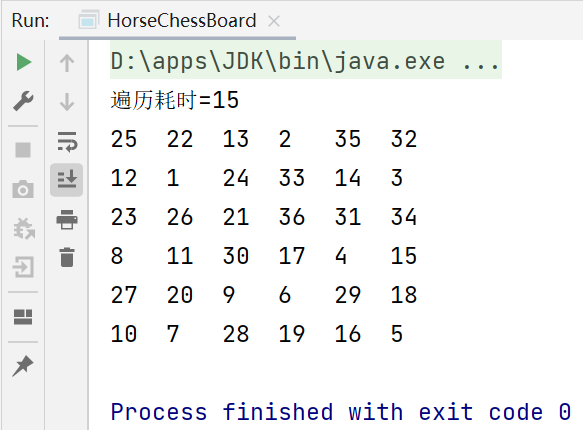
        System.out.println("遍历耗时="+(end - start));
        //输出当前棋盘的情况
        for (int[] rows : chessBoard) {
            for (int step : rows) {//step表示 这个位置是马儿应该走的第几步
                System.out.print(step + "\t");
            }
            System.out.println();
        }
    }

    //最核心的算法，遍历棋盘，如果遍历成功，就将finished的值设置为true，
    //并且将马儿走的每一步step记录到chessBoard
    public static void traversalChessBoard(int[][] chessBoard, int row, int col, int step) {
        //先将step记录到chessBoard
        chessBoard[row][col] = step;
        //把这个位置设置为已经访问
        visited[row * X + col] = true;//就是将二维数组的下标对应到一位数组下标，按行的顺序存放（注意下标从0开始）
        //获取当前位置可以走的下一个位置有哪些
        ArrayList<Point> ps = next(new Point(col, row));//注意col-X,row-Y
        //遍历
        while (!ps.isEmpty()) {
            //取出当前ps集合的第一个位置（点）
            Point p = ps.remove(0);//每取出一个点，就从集合中删除这个点
            //判断该点的位置是否走过，如果没有走过，就递归遍历
            if (!visited[p.y * X + p.x]) {
                //递归遍历
                traversalChessBoard(chessBoard, p.y, p.x, step + 1);
            }
        }
        //当退出while循环后，看看是否遍历成功，如果没有成功，就重置相应的值，然后进行回溯
        if (step < X * Y && !finished) {
            //重置
            chessBoard[row][col] = 0;
            visited[row * X + col] = false;

        } else {
            finished = true;
        }
    }

    //编写方法，可以获取当前位置 可以走的下一步 的所有位置(Point表示x,y)
    public static ArrayList<Point> next(Point curPoint) {//curPoint表示当前点
        //先创建一个ArrayList
        ArrayList<Point> ps = new ArrayList<>();

        //创建一个Point对象，表示一个位置/点，准备放入到 ps集合中
        Point p1 = new Point();

        //判断在curPoint位置，是否可以走如下位置，如果可以走，就将该点(p1)放入到集合ps中
        /**
         * 马走日的话，每个点就有八个方向可以走，并且这八个方向对于当前坐标的相对坐标都是固定的，
         * 通过当前坐标算出八个方向的相对坐标，然后排除掉那些可能会走出界的方向
         */
        //判断是否可以走5位置
        if ((p1.x = curPoint.x - 2) >= 0 && (p1.y = curPoint.y - 1) >= 0) {
            ps.add(new Point(p1));//要创建一个新的点
        }
        //判断是否可以走6位置
        if ((p1.x = curPoint.x - 1) >= 0 && (p1.y = curPoint.y - 2) >= 0) {
            ps.add(new Point(p1));//要创建一个新的点
        }
        //判断是否可以走7位置
        if ((p1.x = curPoint.x + 1) < X && (p1.y = curPoint.y - 2) >= 0) {//注意索引的范围是：0到X-1
            ps.add(new Point(p1));//要创建一个新的点
        }
        //判断是否可以走0位置
        if ((p1.x = curPoint.x + 2) < X && (p1.y = curPoint.y - 1) >= 0) {
            ps.add(new Point(p1));//要创建一个新的点
        }
        //判断是否可以走1位置
        if ((p1.x = curPoint.x + 2) < X && (p1.y = curPoint.y + 1) < Y) {
            ps.add(new Point(p1));//要创建一个新的点
        }
        //判断是否可以走2位置
        if ((p1.x = curPoint.x + 1) < X && (p1.y = curPoint.y + 2) < Y) {
            ps.add(new Point(p1));//要创建一个新的点
        }
        //判断是否可以走3位置
        if ((p1.x = curPoint.x - 1) >= 0 && (p1.y = curPoint.y + 2) < Y) {
            ps.add(new Point(p1));//要创建一个新的点
        }
        //判断是否可以走4位置
        if ((p1.x = curPoint.x - 2) >= 0 && (p1.y = curPoint.y + 1) < Y) {
            ps.add(new Point(p1));//要创建一个新的点
        }
        return ps;
    }
}

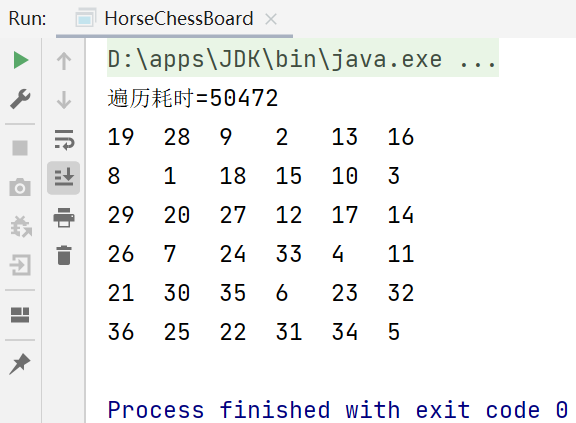
4.优化

1. 根据上面的代码，当前点走的下一个位置，是按照我们的顺时针方向来挑选位置的，因此，所选择的点的下一个可以走的位置的个数是不确定的
2. 优化的思路是：我们应该优先选择的下一个位置，这个位置的再下一个位置应该尽可能少，这样就可以减少回溯的次数
3. 代码：对ps集合按照可以走的下一个位置的次数进行升序排序(从小到大排序)

修改：

1. 编写方法

//写一个方法，对ps集合的各个位置，可以走的下一个位置的次数进行排序，把可能走的下一个位置从小到大进行排序
public static void sort(ArrayList<Point> ps){
    ps.sort(new Comparator<Point>() {
        @Override
        public int compare(Point o1, Point o2) {
            return next(o1).size()-next(o2).size();
        }
    });
}

2. 在递归中调用该方法，对ps集合按照可以走的下一个位置的次数进行升序排序(从小到大排序)

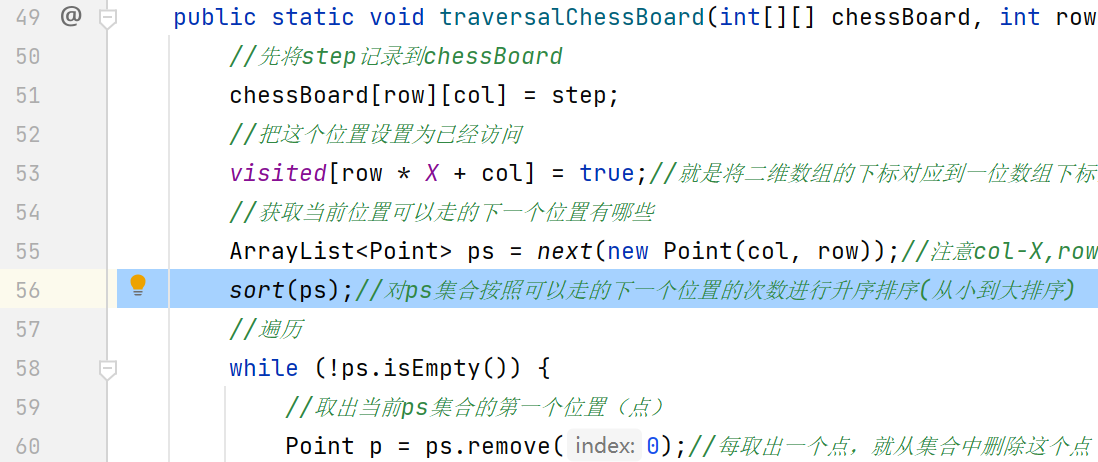
优化结果：

标签：ps,p1,Point,马踏,棋盘,算法,curPoint,位置,day53
From： https://www.cnblogs.com/liyuelian/p/16826320.html