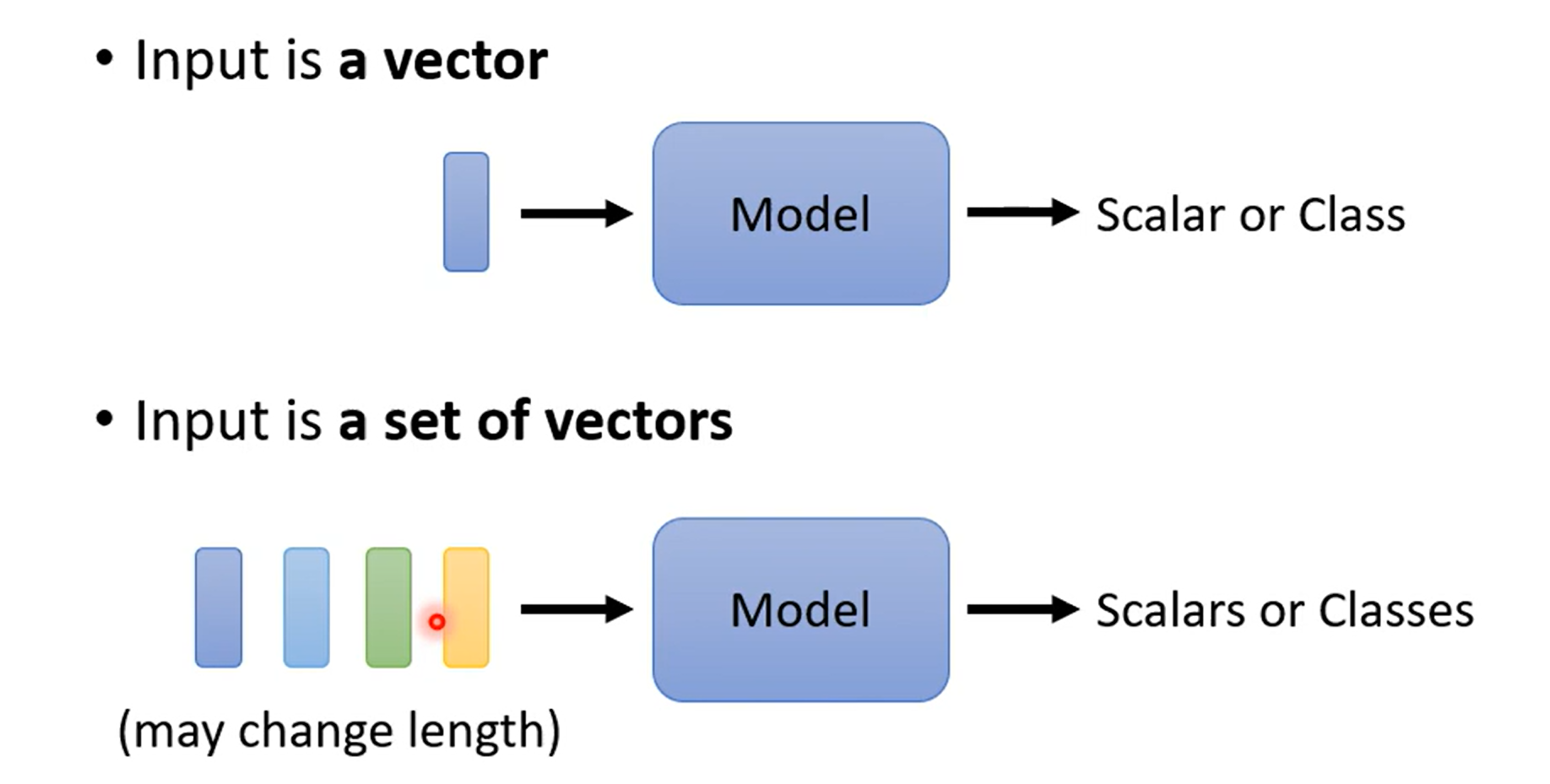
自注意力机制（self-attention）

自注意力机制

self-attention

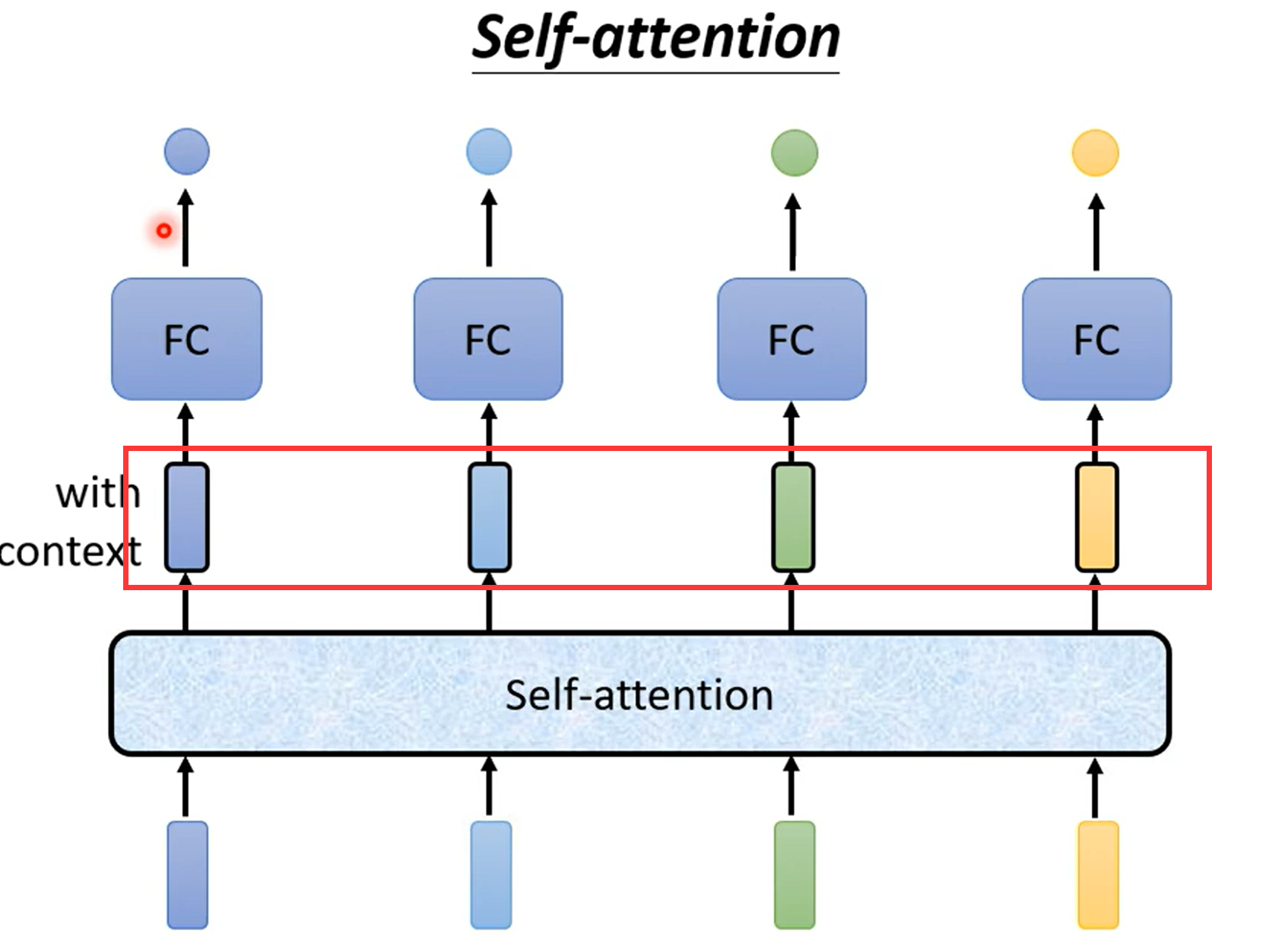
红色框中的这四个向量是考虑了整个sequence后的输出，而且self-attention不仅可以使用一次，

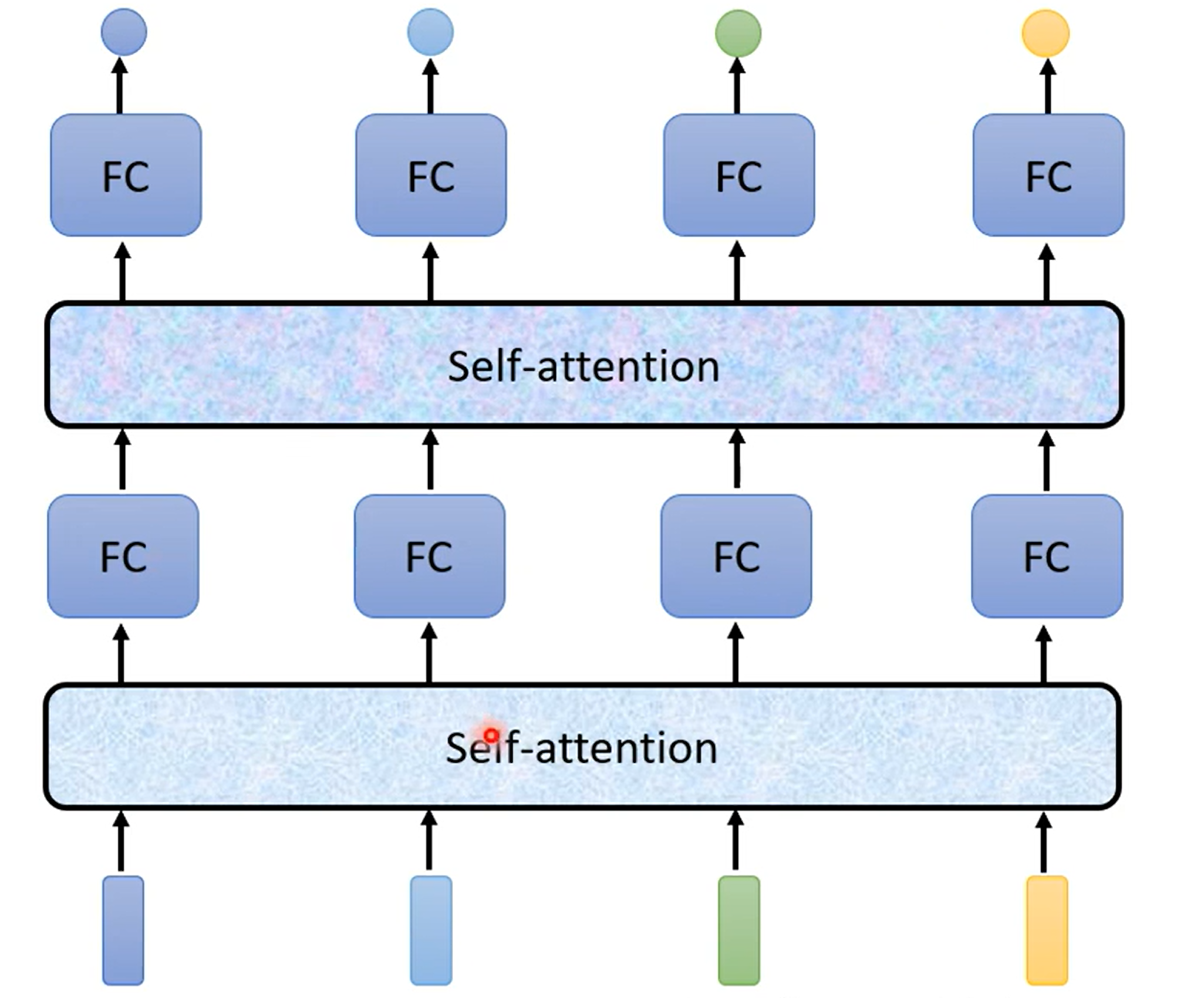
transformer中最重要的就是self-attention

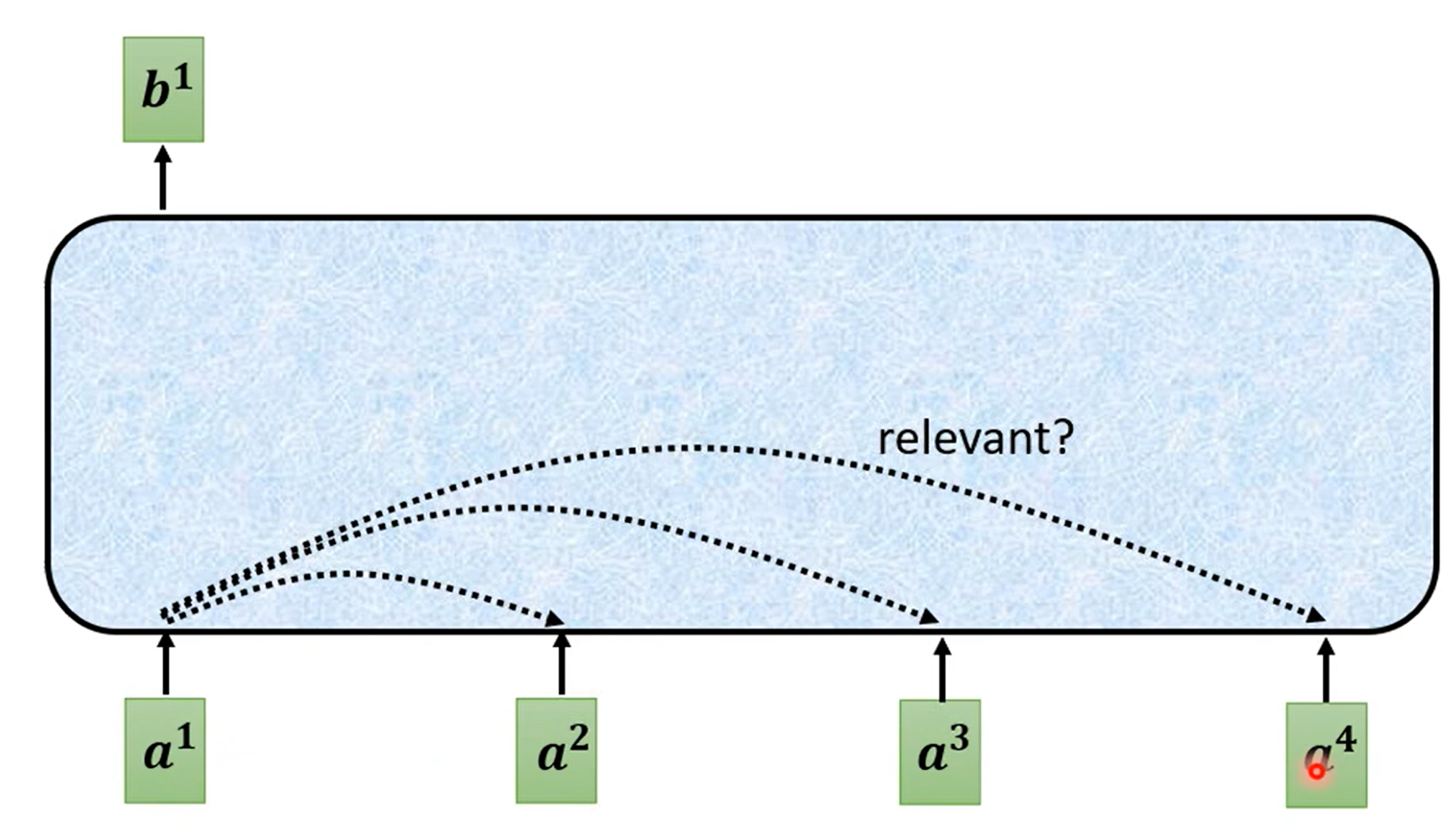
根据\(a^1\)找到和\(a^1\)相关的向量，比如如何计算\(a^1\)和\(a^4\)有多相关

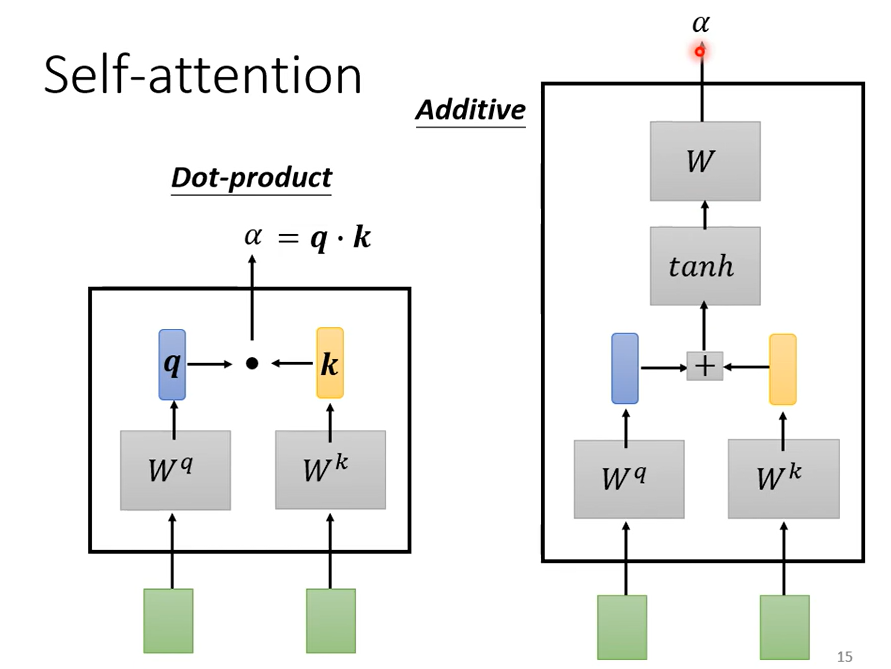
计算有很多不同的方法计算相关度\(\alpha\)，但主要是左边这种方法

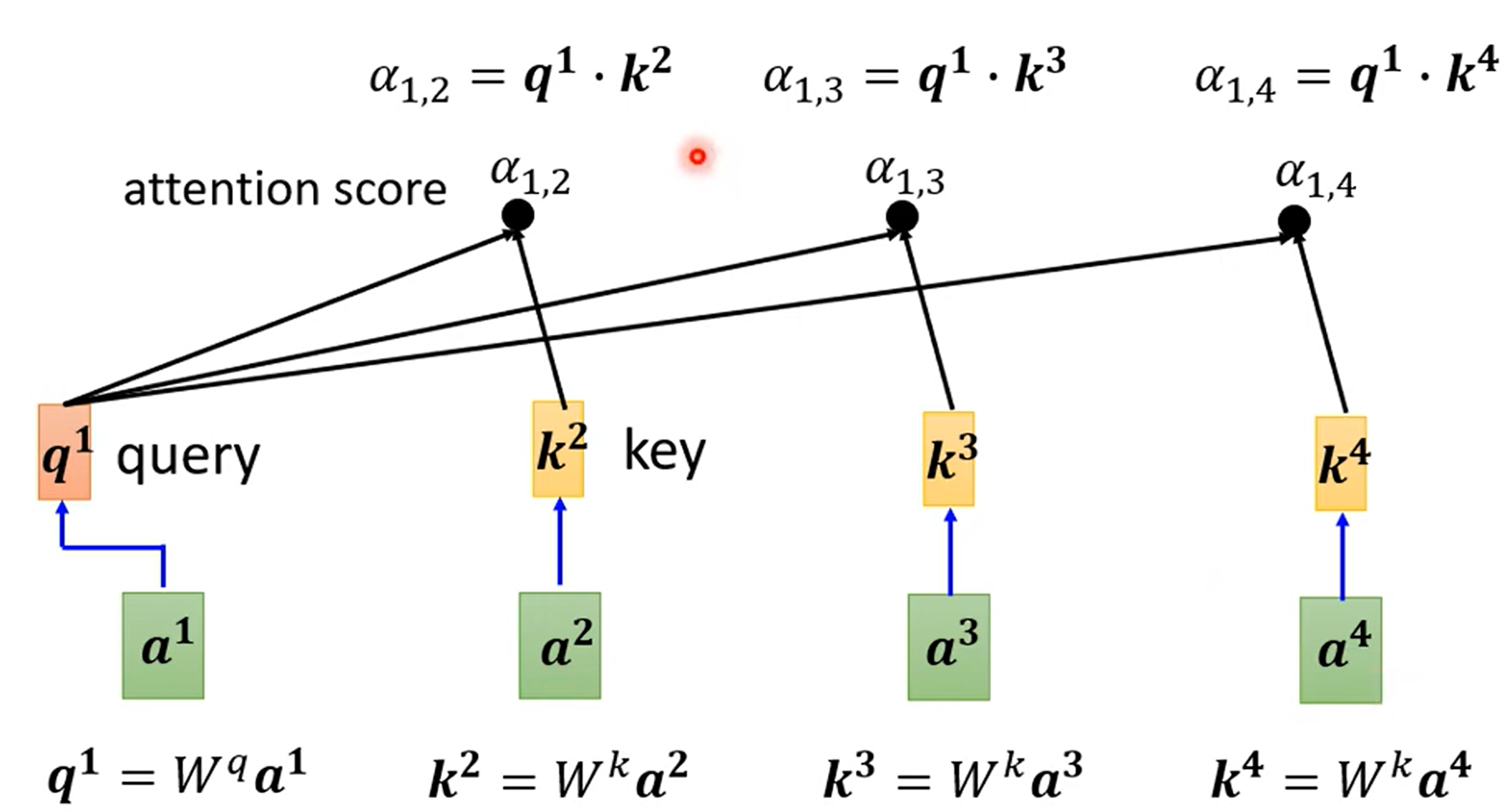
\(\alpha\)也叫attention score，实际上通常还要计算和自己的关联性

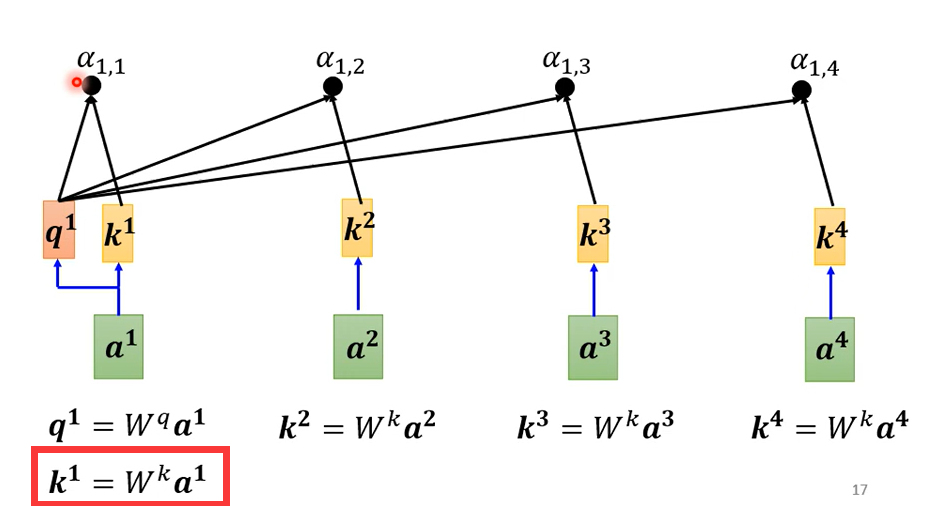
然后加上一个softmax

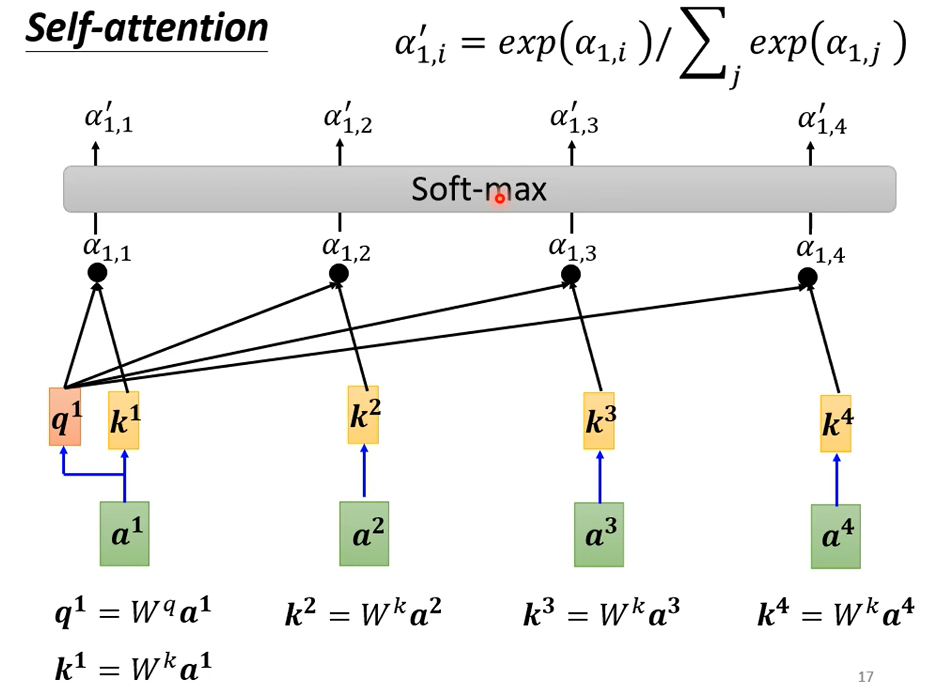
你也可以不用softmax

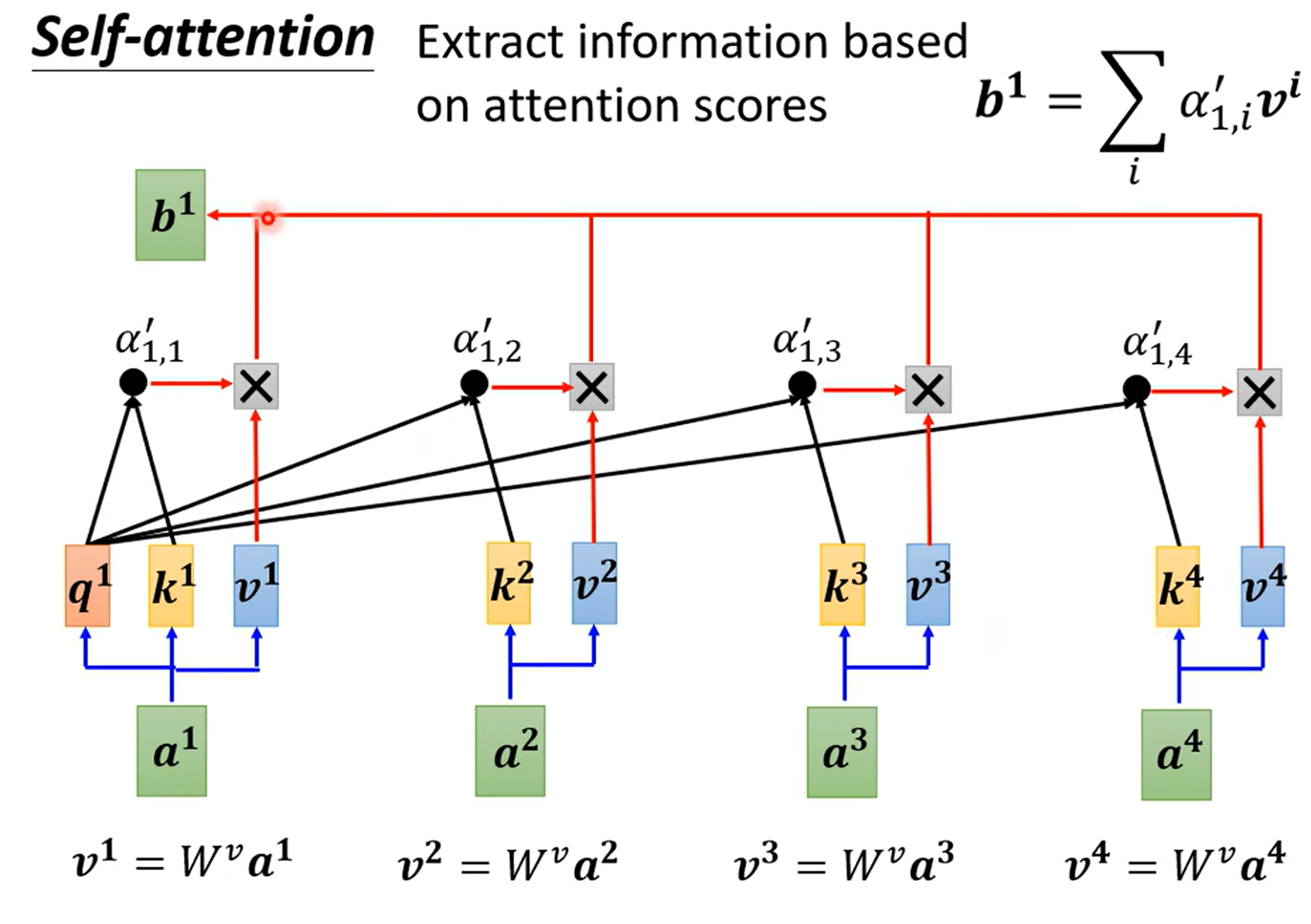
如果关联性比较强，比如\({\alpha}'_{1,2}\)得分高，那么\(b^1\)就更接近\(v^2\)

需要说明的一点是\(b^1，b^2，b^3，b^4\)不需要依序产生，不需要先算\(b^1\)，然后再算\(b^2\)。\(b^1，b^2，b^3，b^4\)是同时得到的

现在计算\(b^2\)，\(a^2\)×权重参数w得到\(q^2\)

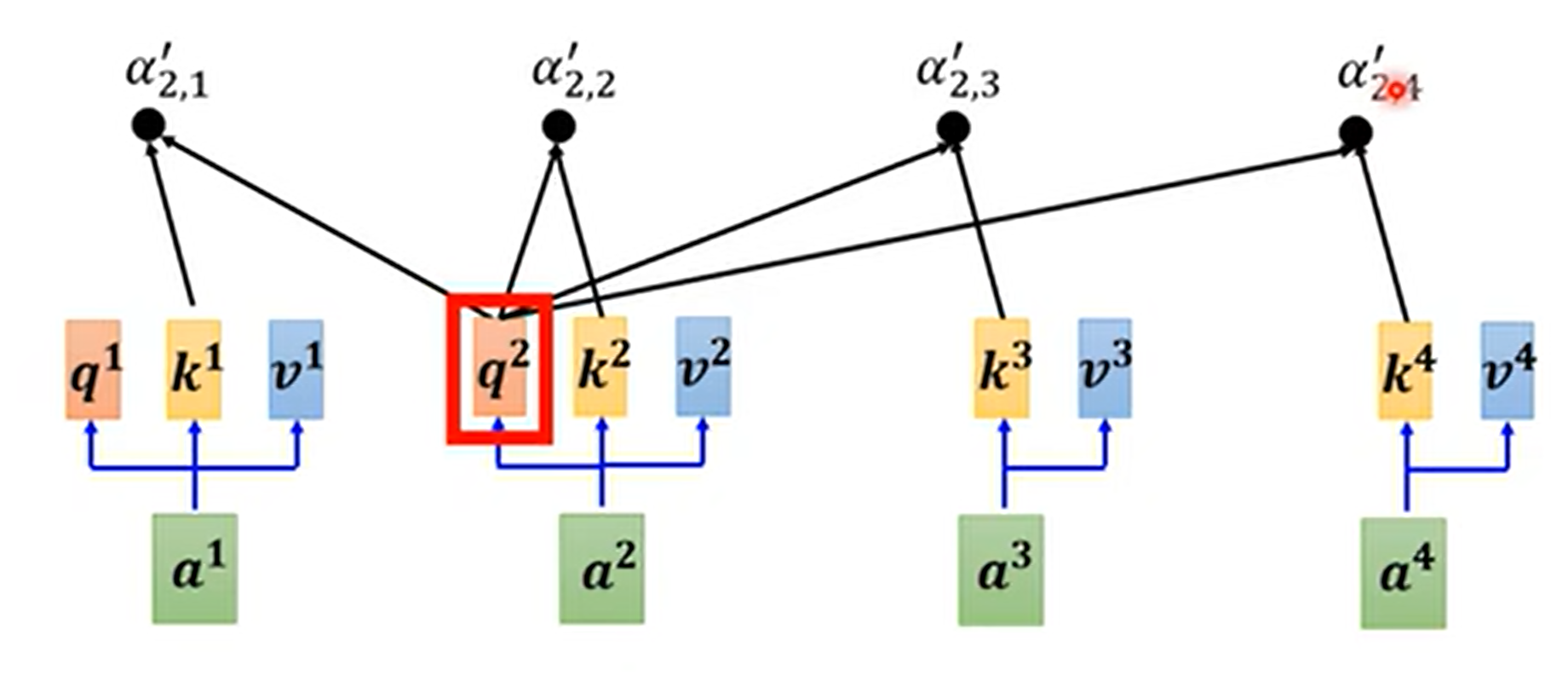
然后

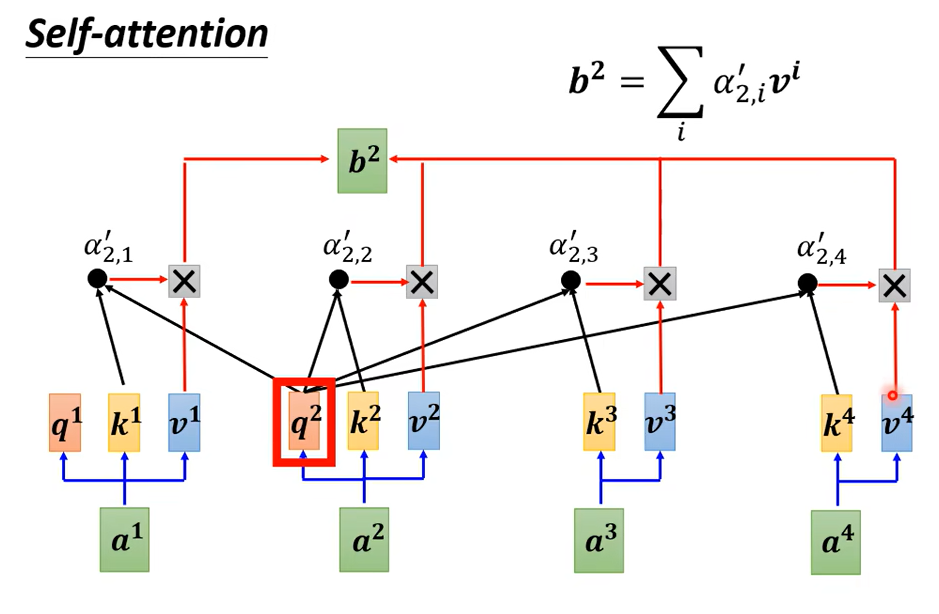
接下来从矩阵乘法的角度再从新过一遍self-attention

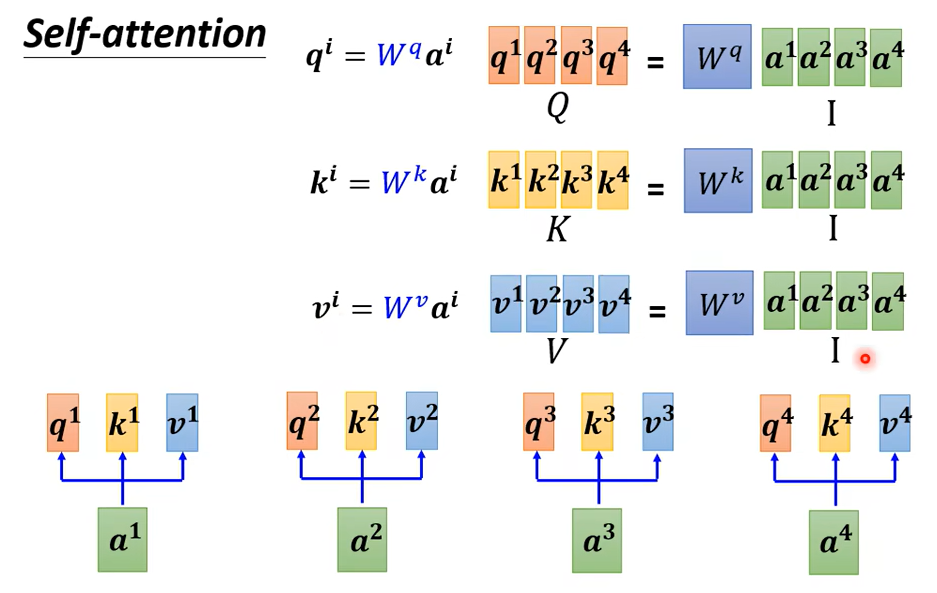
得到qkv后，计算\({\alpha}\)

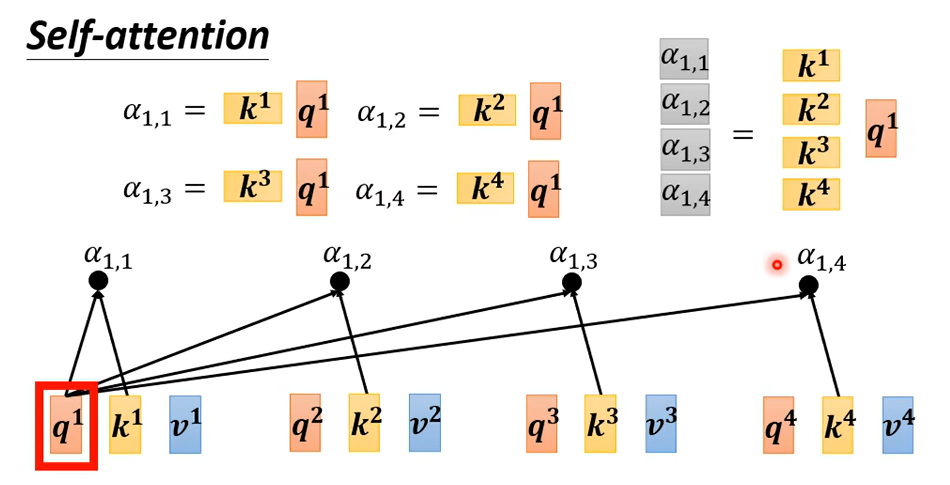
然后一样的操作

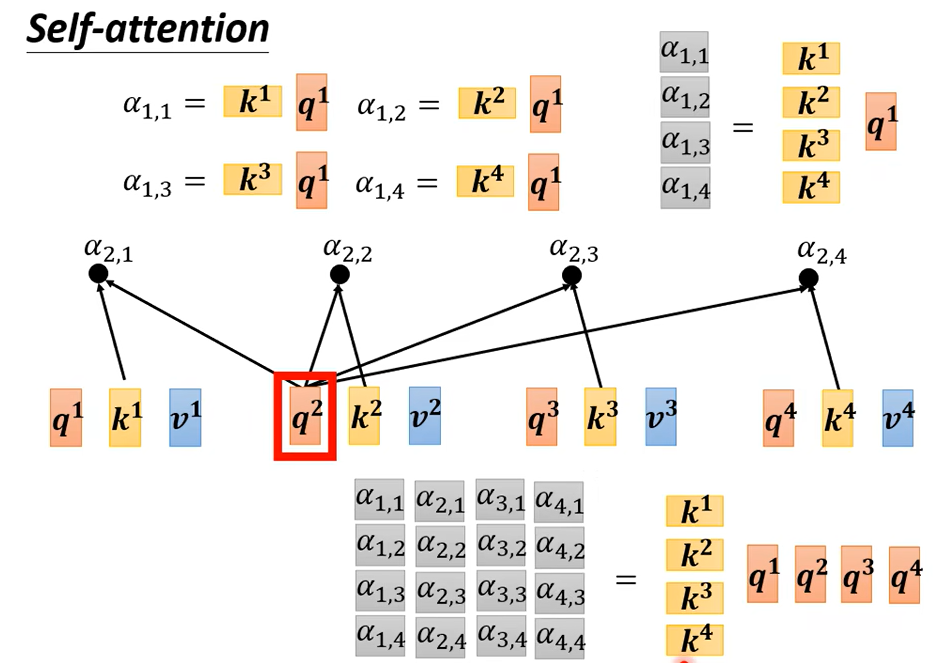
得到\({\alpha}\)矩阵后，进行softmax，使和为1

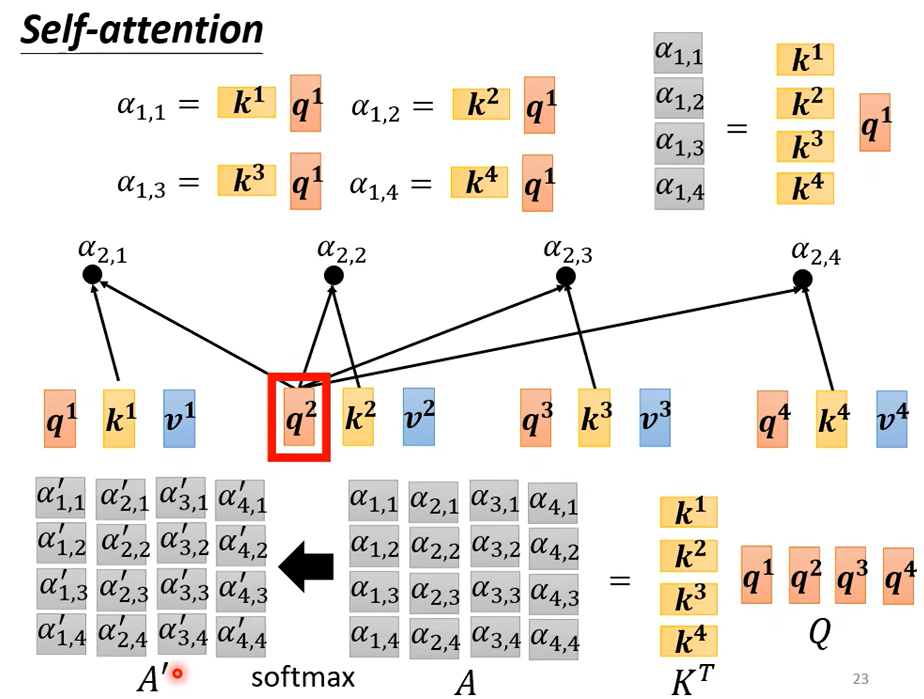
得到\(A'\)后

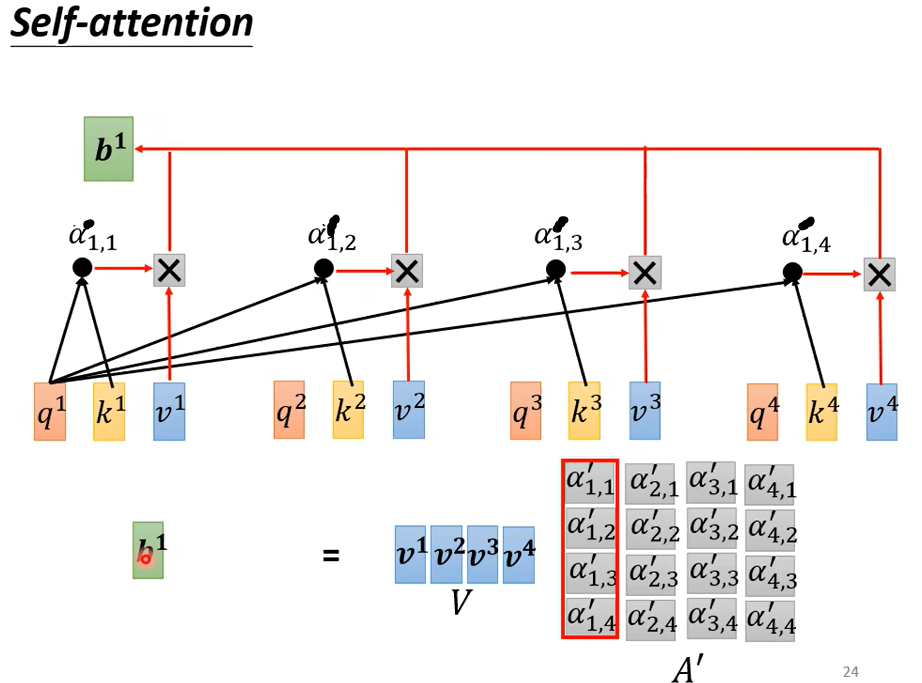
再回顾一下，I是输入，是一排的\({\alpha}\)拼接起来

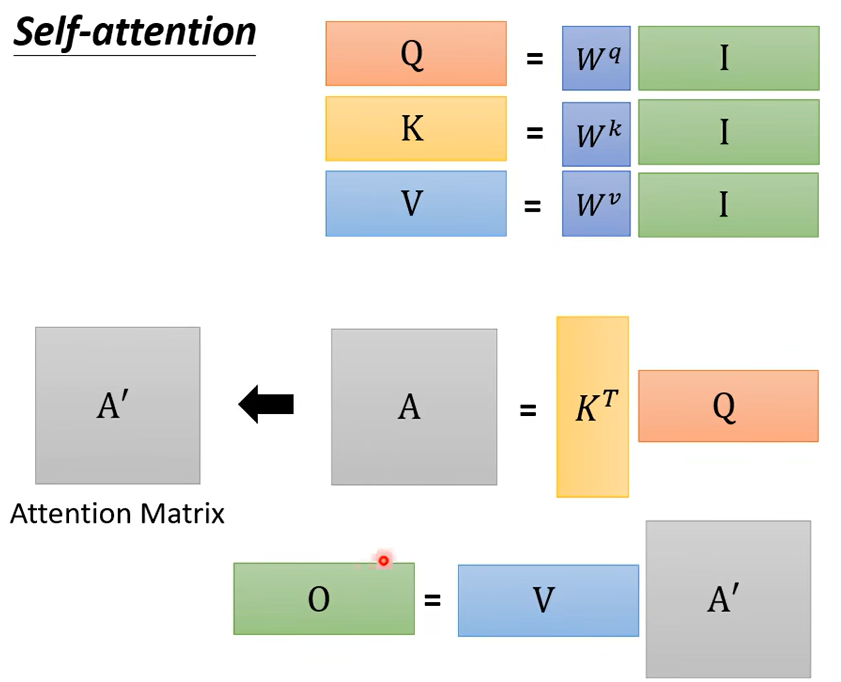
输入是I，输出是O。虽然self-attention看起来做了很复杂的操作，但实际需要学习的参数只有三个矩阵

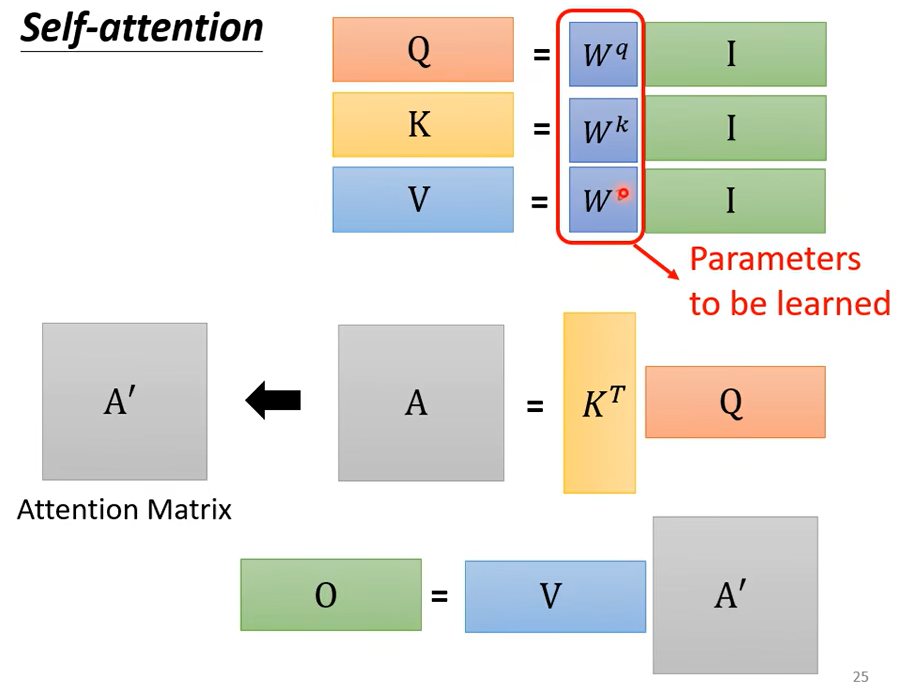
self-attention还有一个进阶版本multi-head Self-attention。

我们之前找相关是通过q找相关的k，但是相关有很多不同的形式，

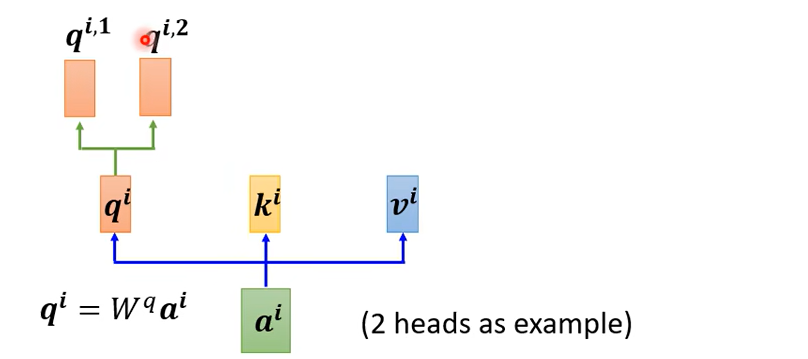
把\(q^i\)乘以两个不同的矩阵得到\(q^{i,1},q^{i,2}\),q有两个，那么对应的k和v也有两个

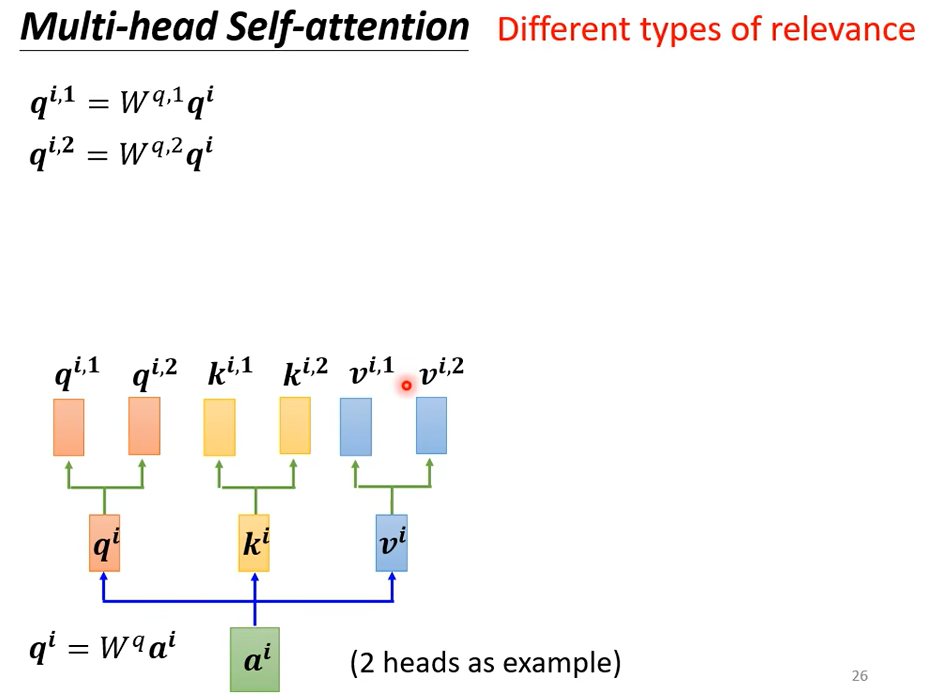
具体是怎么计算的呢

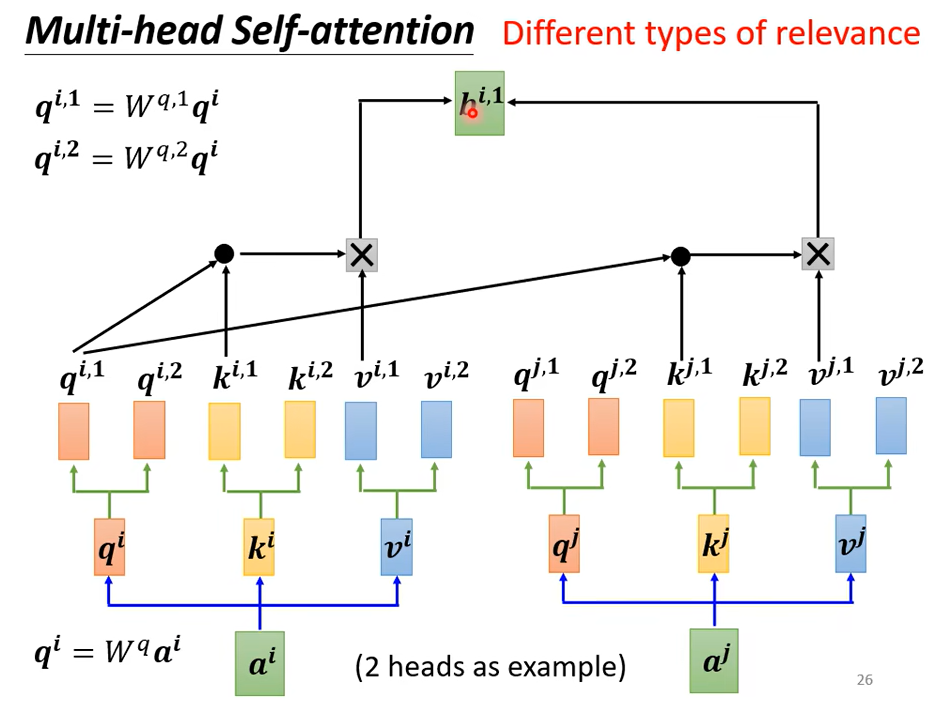
\(q^1\)算attention分数的时候只需要管\(k^1\)不需要管\(k^2\)。

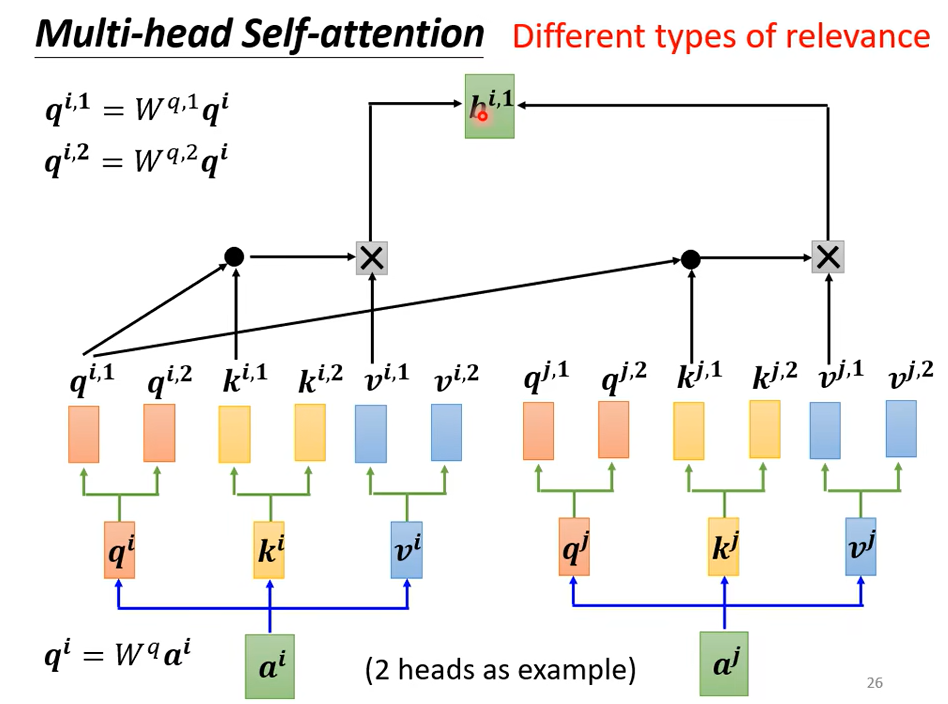
同样的得到attention分数后，只需要乘以\(v^1\),得到\(b^{i,1}\),这只用到了一个head，另一个head也做一样的事情

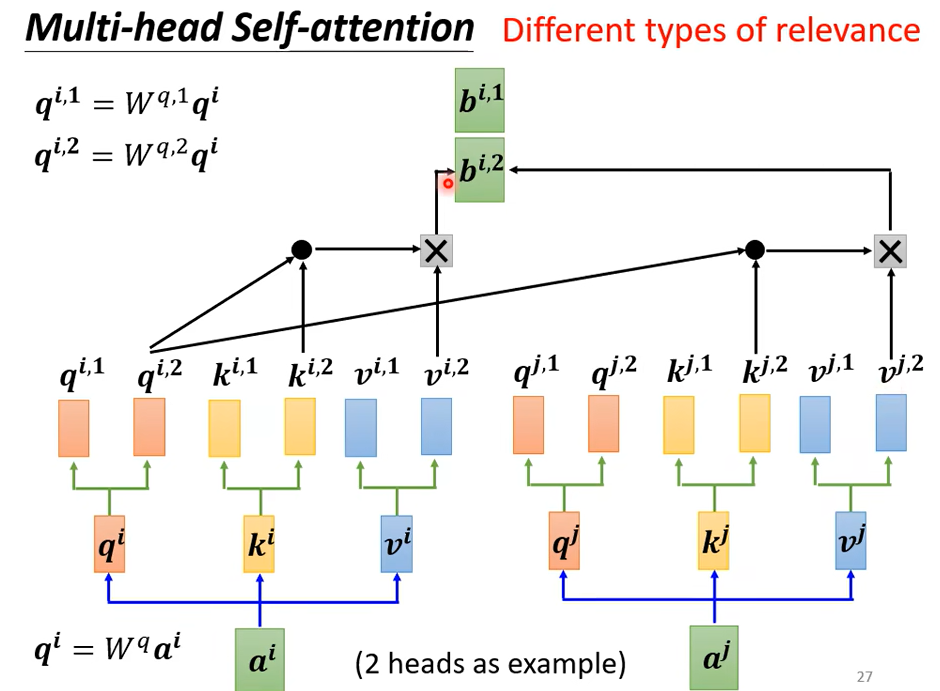
接下来把\(b^{i,1}\)和\(b^{i,2}\)拼在一起，乘以一个矩阵，得到\(b^i\)传到下一层

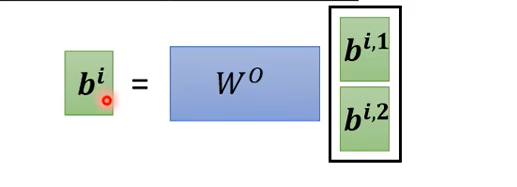
这就是multi-head Self-attention。但是现在有个很重要的问题，就是没有位置信息，输入\(a^1,a^2,a^3,a^4\)是在seq的最前面还是最后面？

虽然我们给它们标了1234，但只是为了方便理解，对于神经网络来说，它并不知道\(a^1,a^2,a^3,a^4\)哪个在前哪个在后。所以你做Self-attention的时候，如果觉得位置信息是个重要的信息，可以把位置信息加上

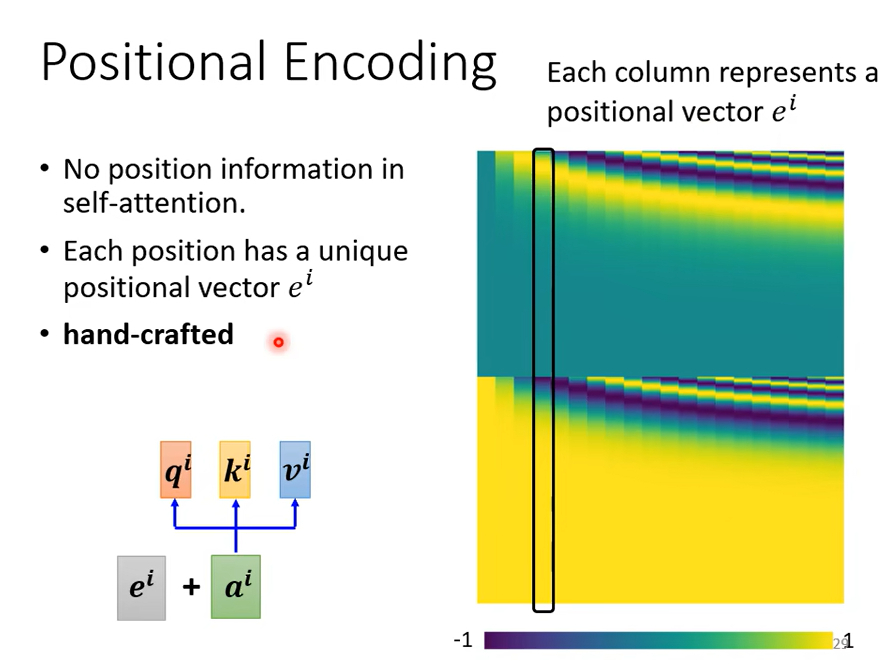
每个位置给一个独特的vector 也就是 \(e^i\)，但是这种方法是人为的，人设的vector就有很多的问题，比如vector设到128，但是sequence有129。论文中vector是通过一个sin cos的函数产生的，当然你可以采用其他的方法，位置vector的设置还是一个有待研究的问题，你可以创造新的方法。有篇文章详细的比较了不同的position vector

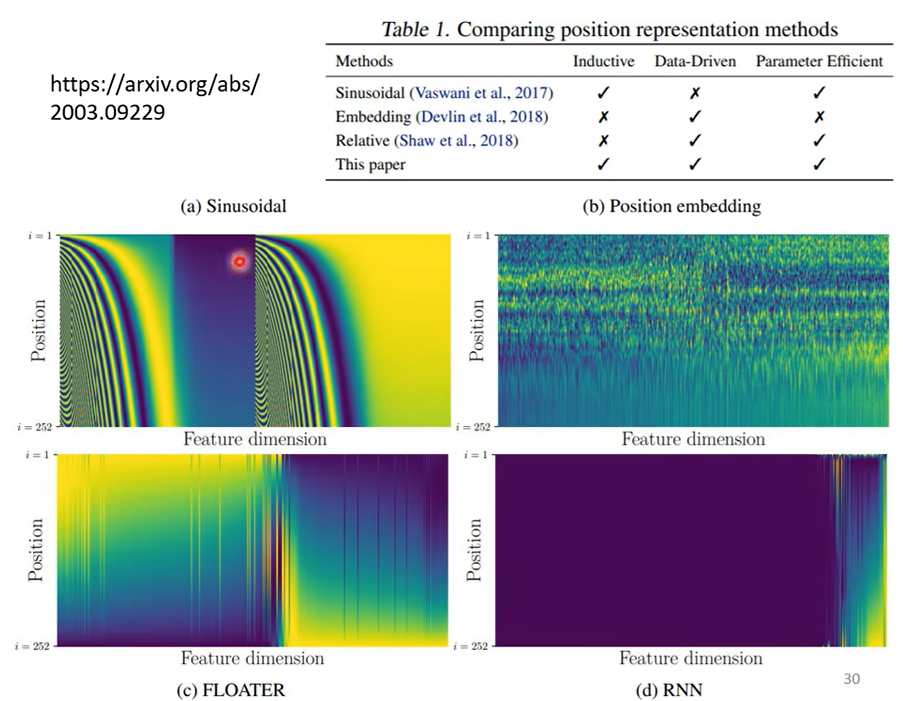
每一行代表一个vector，a是最原始的，b是学习出来的，c是使用一个神奇的网络，d是通过rnn学习的

self-Attention在NLP的应用，大家耳熟能详

但是self-Attention不只能用在NLP相关领域，也可以用在其他方面，比如做语音的时候，但是在做语音的时候，你可能会对self-Attention有一个小小的改动，因为用vector表示语音信号，向量的长度会非常大，因为用一个向量表示10ms的语音信息，那么1s的语音就有100个vector，5s就是500个vector，随便一句话可能就成千个vector了，

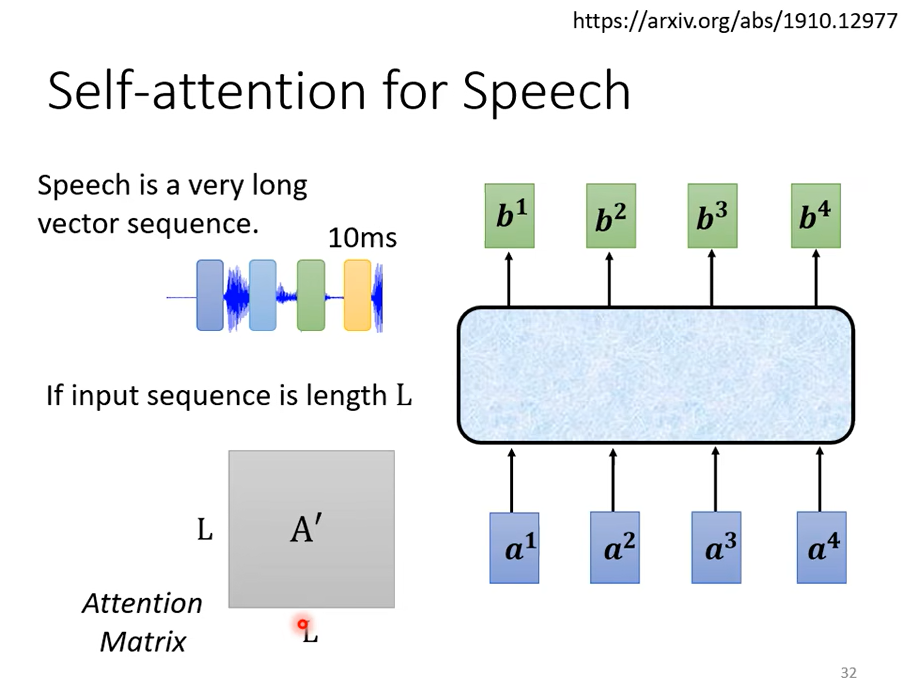
如果长度很大，Attention Matrix就很大，要计算\(L^2\),计算量大，而且消耗的内存也大.所以做语音识别的时候，有一个叫Truncated Self-attention。

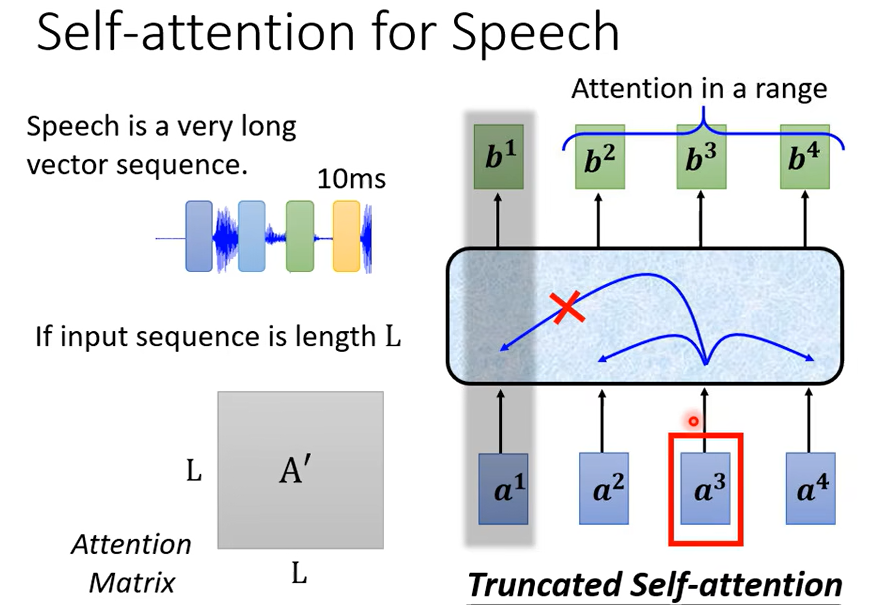
不需要看整个句子，只需要看一部分即可（人为设定的），但是我们是怎么知道需要一部分就好，那就取决于你对这个问题的理解。

Self-attention还可以被应用在图像上，我们目前讲的Self-attention都是适合在输入是一排向量的时候，但我们也可以把图像看成是vector set

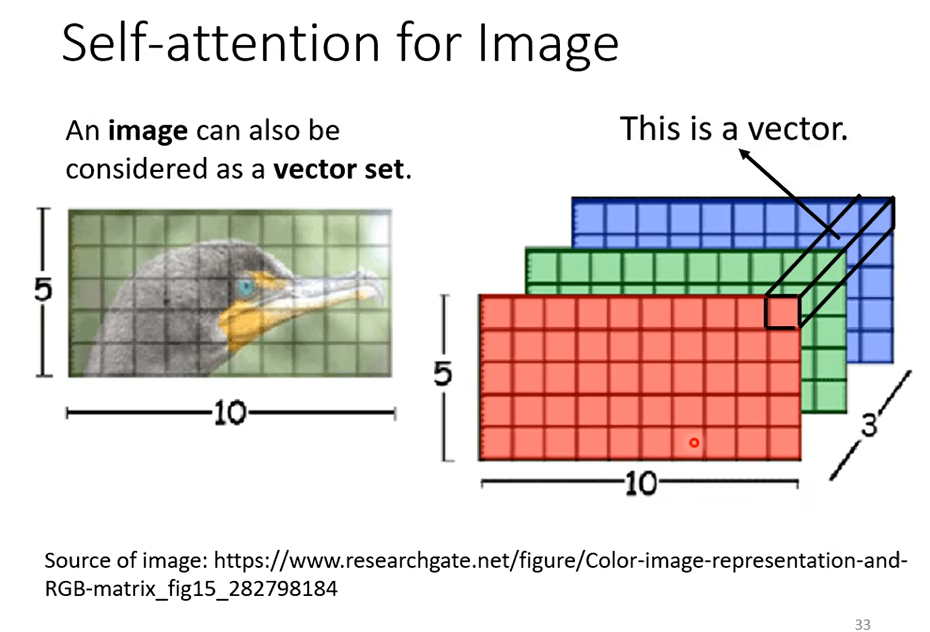
我们可以把图像的每个位置看成一个三维的向量，那么就是一个50个向量的vector set，从这个角度看，图像就是一个vector set，那么就能用Self-attention。已经有人这么做了

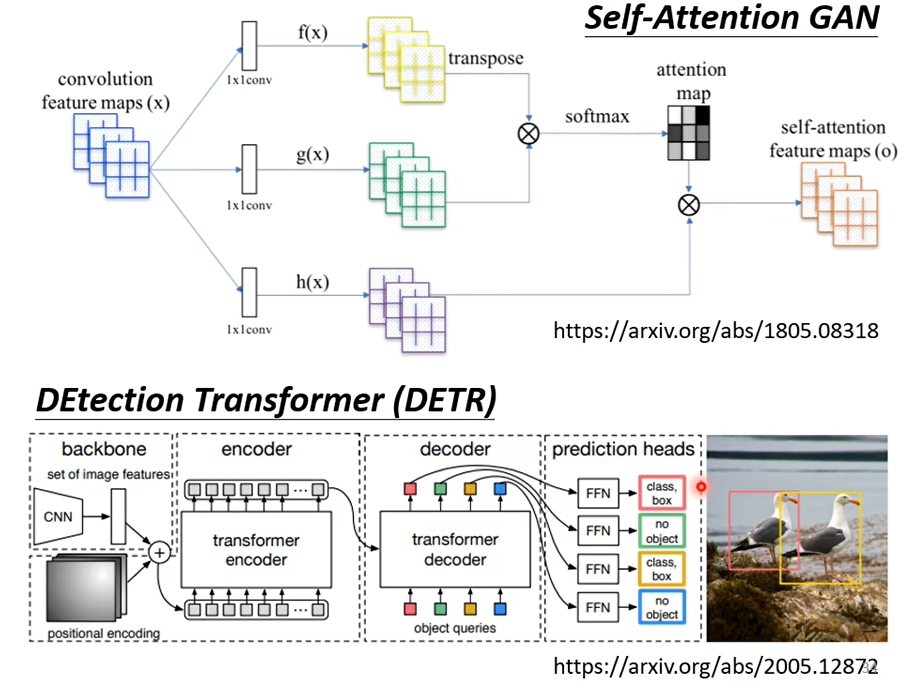
比如1这个像素点产生query，0这个像素点产生key，那么我们考虑就是整张图像

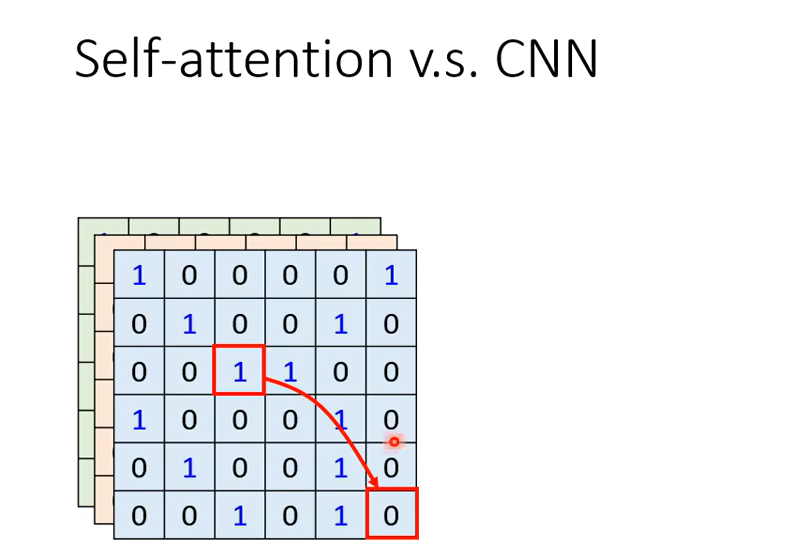
这么看的话，CNN更像是简化版的Self-attention，因为CNN只考虑了卷积核范围内的数据

下面这篇文章会用数学严谨的方式告诉你

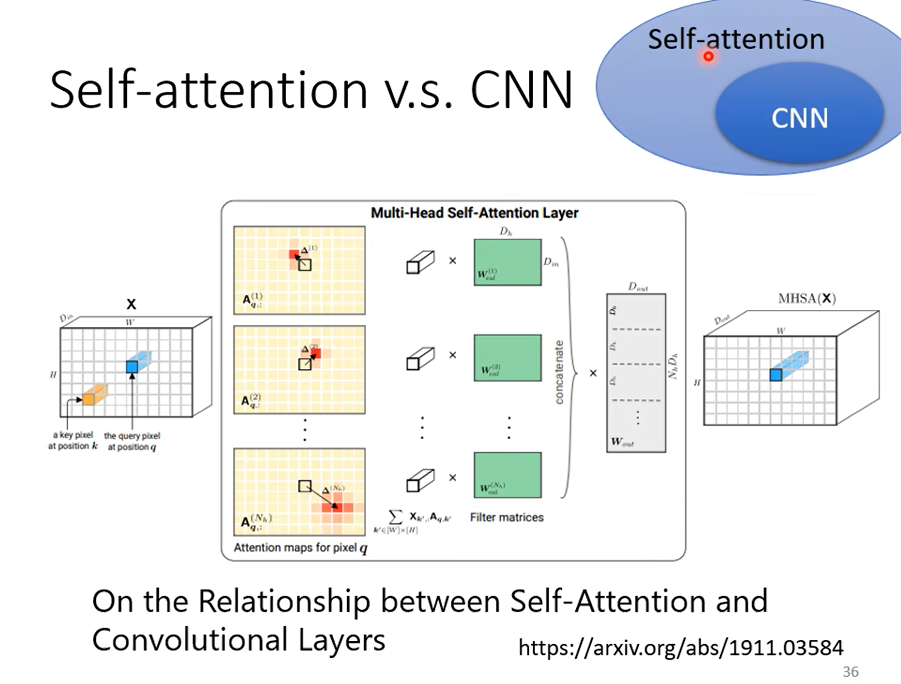
只要设置合适的参数，Self-attention可以做到和CNN一样的事，可以发现Self-attention比CNN更加灵活，但是更灵活的model需要更多的data，否则容易过拟合，而有限制的模型可能在数据小的时候也不会过拟合。

16×16的patch（图像的一个块），每个patch就看成一个word

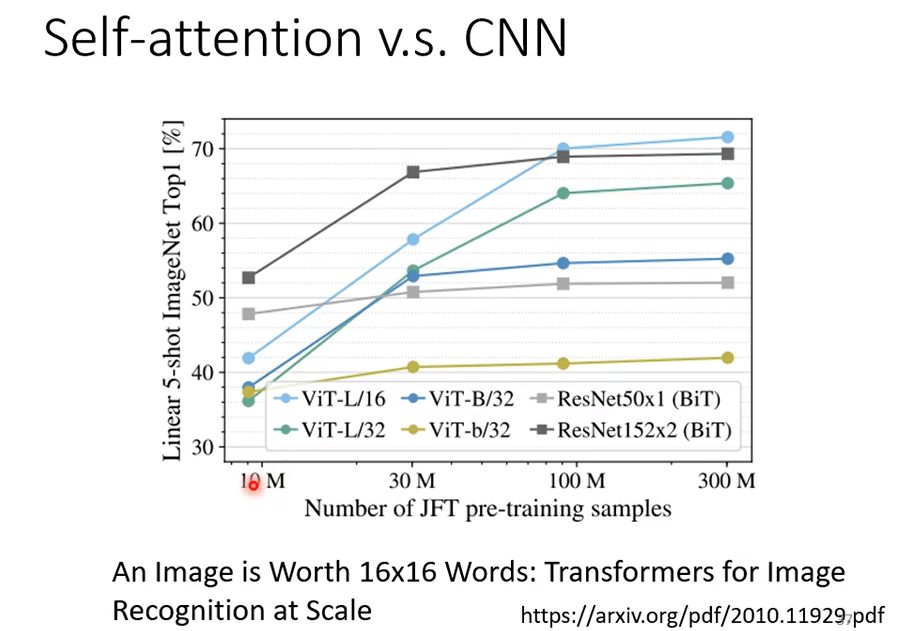
最小的数据量是10M，一千万张图

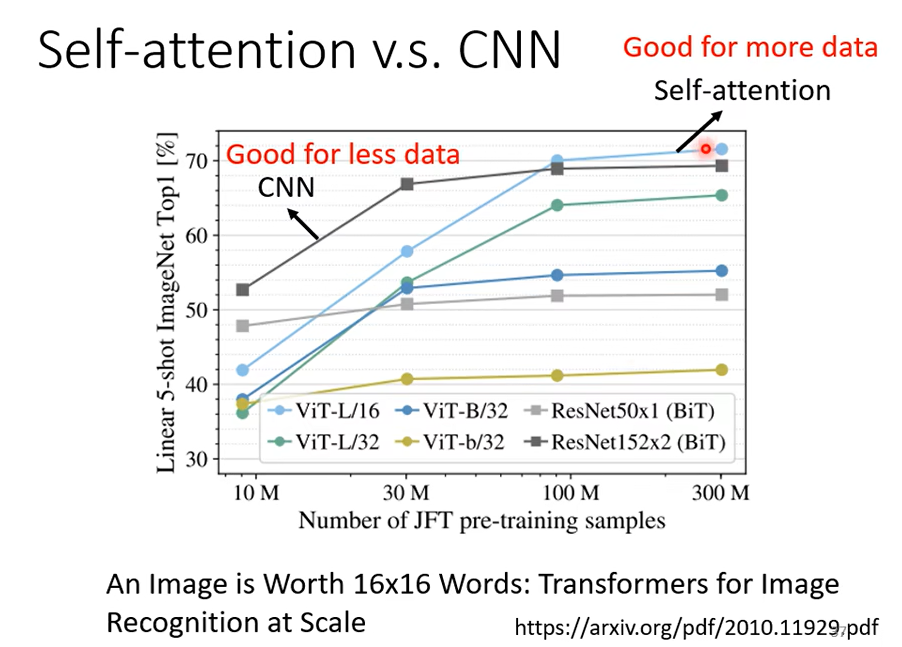
RNN和Self-attention的区别

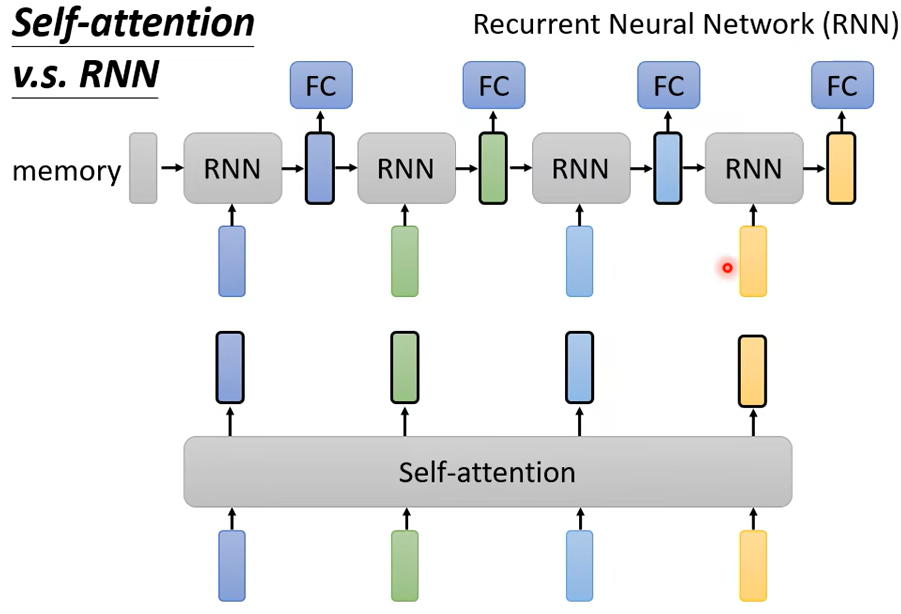
Self-attention每一个都考虑了整个sequence而，RNN只考虑了左边的vector，不过RNN也可以用双向的。不过把RNN的output和Self-attention的output对比的话，即使使用了bidirectional的RNN，还是有一定差别。

对于RNN的输出，想要考虑最左边的输入，需要存在memory里，一直不能忘记，一直带到最右边，才能在最后一个时间点被考虑，但对Self-attention来说没有这个问题

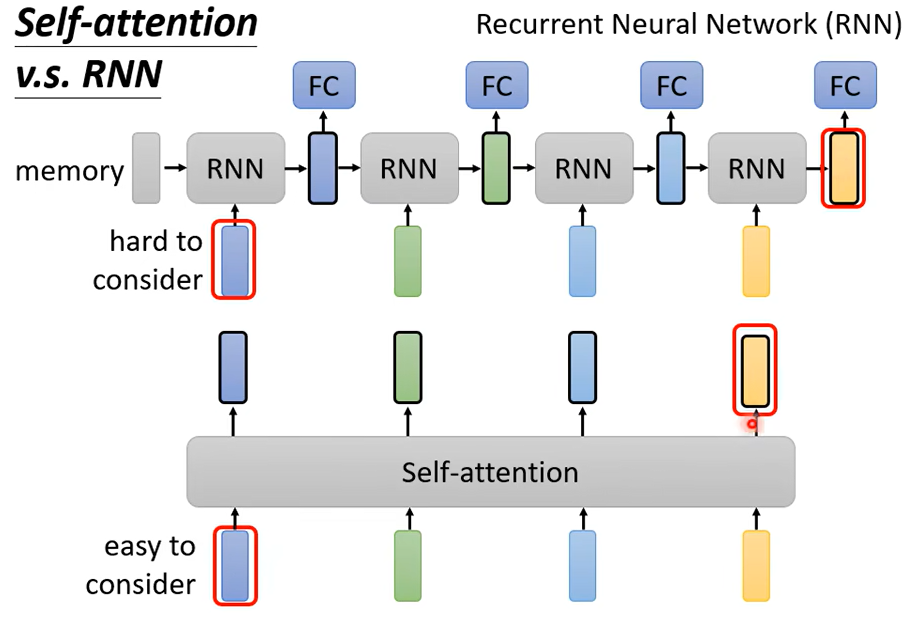
还有就是RNN没办法平行处理，必须先产生前面的向量

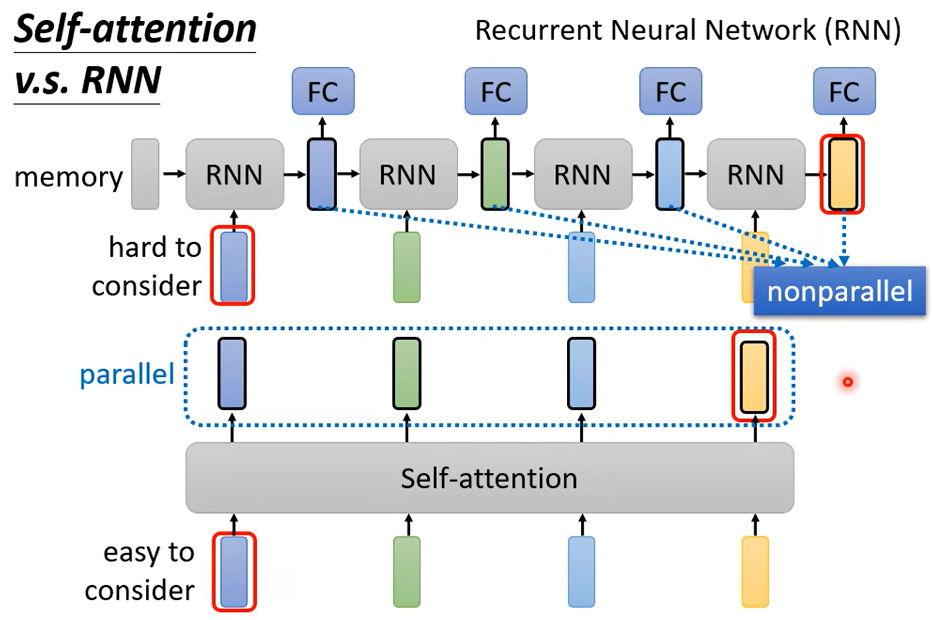
而Self-attention可以同一时间一次性生成这些向量，所以运算效率上，Self-attention比RNN更有效率。想进一步了解RNN和Self-attention可以看下面这篇文章
Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention
最后，Self-attention也可以用在Graph上面

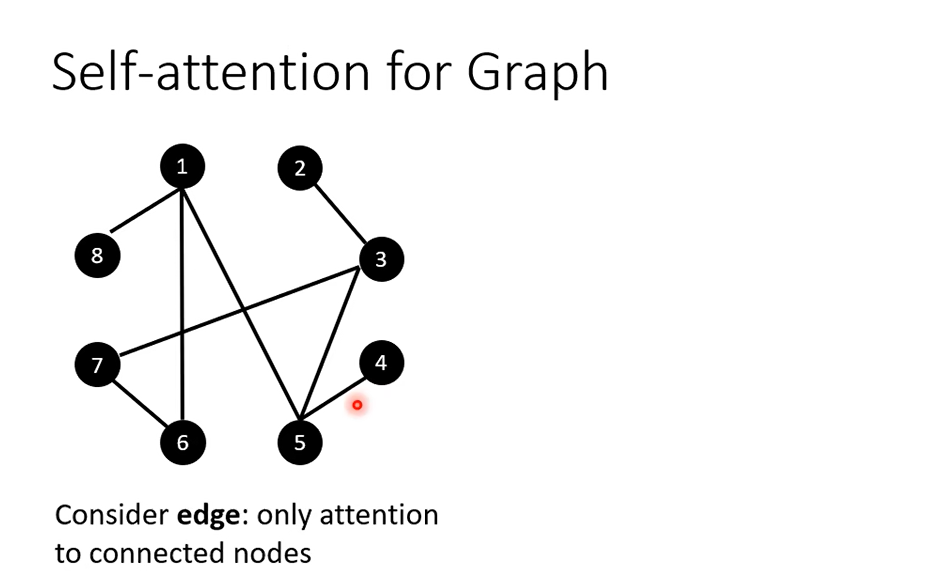
每一个node可以表示为一个vector，因为graph有edge的信息，所以不需要attention去找关联性，所以在计算

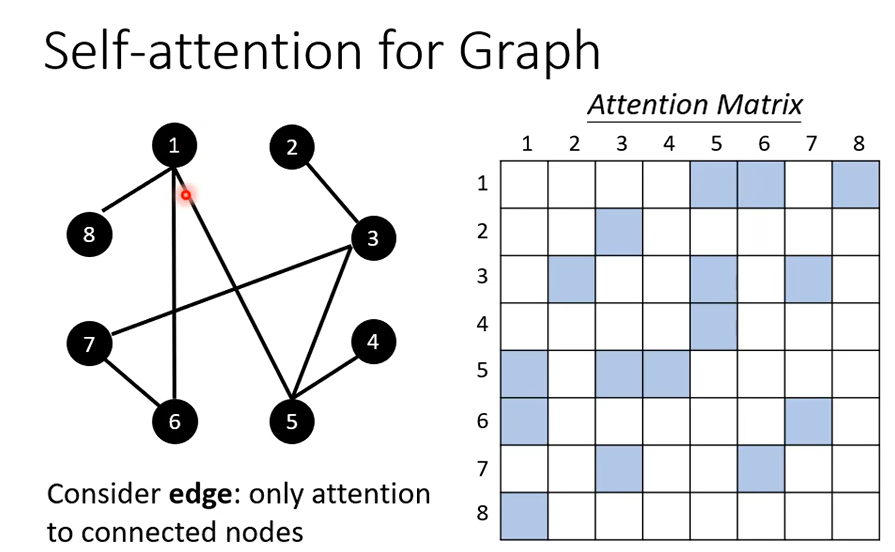
Attention Matrix的时候只需要计算有edge相连的node, 根据domain knowledge没有相连的我们直接设置为0

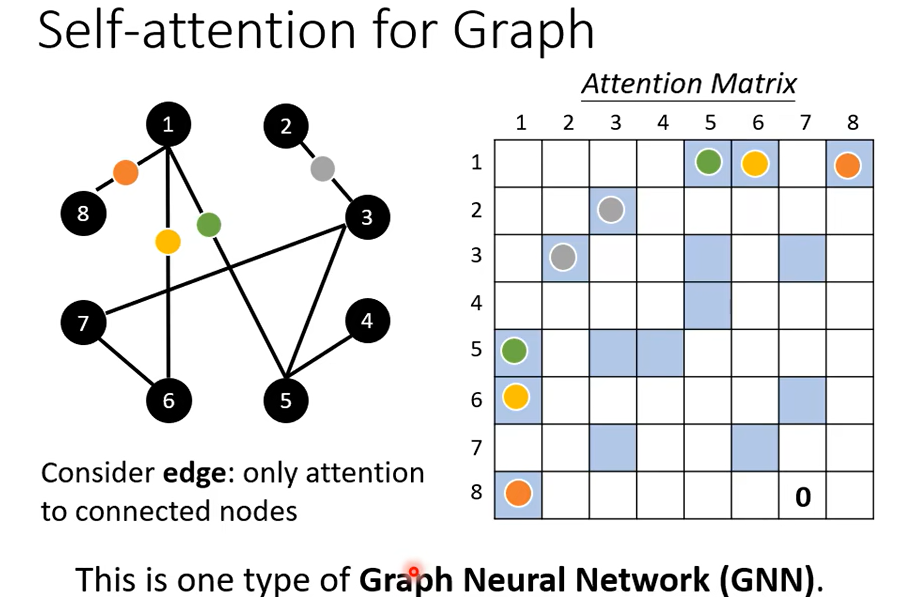
Self-attention也有非常多的变形

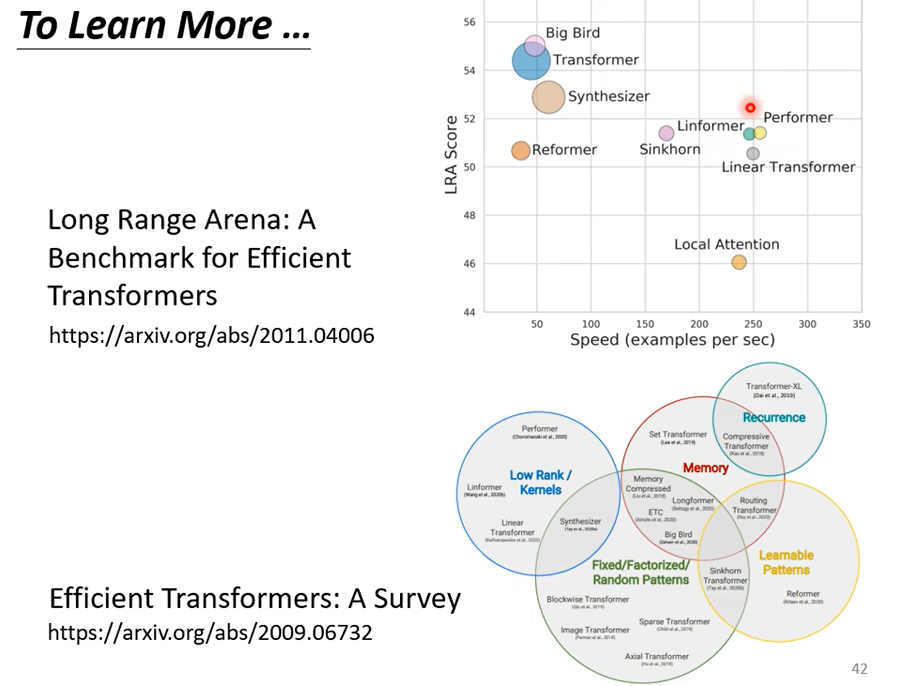
Self-attention的最大问题就是运算量非常大