之前做了一道高维前缀和题做着做着忘掉怎么写了,遂记一发。
你说的对,但是我谈的真的很浅。
铺垫
回忆一下我们求前缀和是怎么求的。
一维前缀和:
for(int i=1;i<=n;i++){
s[i]=s[i-1]+a[i];
}
没有任何问题对吧。
而求二维前缀和时,我们通常会使用如下方法求前缀和(如果不是当我没说):
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
}
}
本质上是在做一个容斥。
三维前缀和的式子更长:
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
for(int k=1;k<=n;k++){
s[i][j][k]=s[i-1][j][k]+s[i][j-1][k]+s[i][j][k-1]-s[i-1][j-1][k]-s[i-1][j][k-1]-s[i][j-1][k-1]+s[i-1][j-1][k-1]+a[i][j][k];
}
}
}
如果维度接着升高,那么这种常规方法我们就要枚举子集做容斥,时间复杂度来到了 \(O(n^w2^w)\)。
我们考虑另一种方法:
先对于每一维,求出仅考虑这一维上的前缀和;接着考虑另一维,再求出仅考虑这一维上的前缀和,写成代码是这样子的(以二维前缀和为例):
for(int i=1;i<=n;i++)s[i][j]=a[i][j];
for(int i=2;i<=n;i++)for(int j=1;j<=n;j++)s[i][j]+=s[i-1][j];
for(int i=1;i<=n;i++)for(int j=2;j<=n;j++)s[i][j]+=s[i][j-1];
关于正确性,我选择从 https://zhuanlan.zhihu.com/p/651143987 嫖一个图过来:
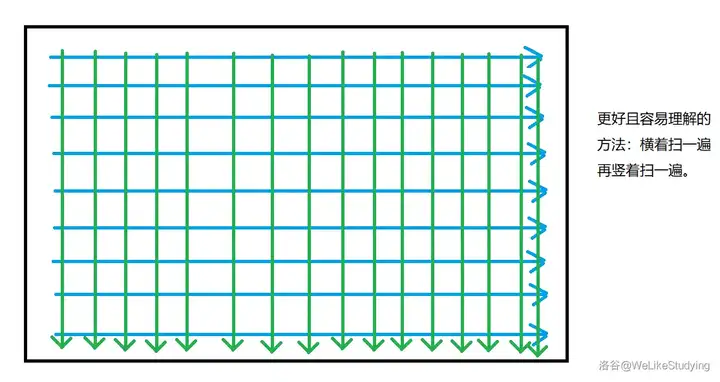
于是时间复杂度降到了 \(O(n^ww)\),这就是高维前缀和的核心思路。
问题引入
给定 \(2^n\) 个数 \(a_i\),从 \(0\) 开始标号。令 \(f_S\) 为 \(\sum_{T\operatorname{or} S=S}a_T\),对 \(S=0\sim 2^n-1\) 求 \(f_S\)。
\(n\le 20\)。
分析
显然有一个 \(O(4^n)\) 的暴力。
把 \(S\) 的每一个二进制位记为一个维度,那么 \(f_S\) 就相当于对所有的这 \(n\) 维做高维前缀和,只不过每一维只有 0/1 两种取值。
代码实现:
for(int S=0;S<(1<<n);S++)
for(int i=0;i<n;i++)
if((S>>i)&1)
f[S]+=f[S^(1<<i)];
时间复杂度 \(O(2^nn)\)。
例子:狄利克雷前缀和
题面:https://www.luogu.com.cn/problem/P5495
对所有 \(x=1\sim n\) 求 \(f_x=\sum_{y|x} a_y\)。
\(n\le 2\times10^7\)。
分析
将数 \(x\) 唯一分解成 \(x=p_1^{e_1}p_2^{e_2}\cdots p_k^{e_k}\) 的形式,把每个质因数视为一个维度,对所有维度做一遍高维前缀和。由于每一维的取值是在 \(0\) 到 \(\dfrac{n}{p}\) 之间的,时间复杂度 \(\sum_{p\in prime}\dfrac{n}{p}=O(n\log \log n)\)。
代码实现:
for(int i=2;i<=n;i++){
if(!flag[i]){//flag[i]为质数标记
for(int j=1;i*j<=n;++j){
flag[i*j]=1;
a[i*j]+=a[j];
}
}
}