这是一篇长篇小说
DAY1
除了DAY4-DAY5个别内容以外,这些都是补的,但是全写完有太多了qwq,挑题写了
树状数组和线段树基础
很多都是一些模板题,太模板的题不再做太多解释
题目:
P4062
P6619
P3688
P3157
P10497
P3374
P3368
P4223
P10589
P10688
CF1667B
P10463
SP1716
CF718C
CF446C
P1712
P2572
P9871
CF1527E
P3373
楼兰图腾(BIT逆序对模板)
题目大意:平面上n个点,横纵坐标分别是排列,求下列两种三元组(a,b,c)的数量:
\(1.a_x<b_x<c_x,a_y>b_y,c_y>b_y\)
\(2.a_x<b_x<c_x,a_y<b_y,c_y<b_y\)
先按横坐标排序,然后分别求每个位置纵坐标比它大的前后各有多少个,相乘再求和就是第一类的答案,第二类类似。
这样就转化成了求逆序对,开个值域树状数组跑一下就行
#include"bits/stdc++.h"
#define ll long long
using namespace std;
const int N=200010;
ll n,a[N];
ll ans[N][10],ans_1,blns;
struct tree_array
{
int t[N];
void add(int p,int x)
{
for(;p<=n;p+=p&-p) t[p]+=x;
}
int ask(int p)
{
int res=0;
for(;p;p^=p&-p) res+=t[p];
return res;
}
}t1,t2;
int main(void)
{
scanf("%lld",&n);
for(int i=1;i<=n;i++)
{
scanf("%lld",&a[i]);
ans[i][0]=t1.ask(a[i]-1),ans[i][1]=i-1-t1.ask(a[i]);
t1.add(a[i],1);
}
for(int i=n;i>0;i--)
{
ans[i][2]=t2.ask(a[i]-1),ans[i][3]=n-i-t2.ask(a[i]);
t2.add(a[i],1);
}
for(int i=1;i<=n;i++)
ans_1+=ans[i][1]*ans[i][3],blns+=ans[i][2]*ans[i][0];
printf("%lld %lld",ans_1,blns);
return 0;
}
P4062 [Code+#1] Yazid 的新生舞会
题目大意:求存在绝对众数的区间的数量。
枚举每一种数字,记\(s_i\)表示前缀这种数字的数量
这样转化为统计\(2*(s_r-s_{l-1})>r-l+1\)的数对数量,等价于\(2*s_r-r>2s_{l-1}-(l-1)\) 这样是\(O(n^2log\space n)\)的,只枚举每种数字出现的位置,枚举量是\(O(n)\),现在只考虑一种数字,出现的\(k\)位置将序列划分为\(k+1\)个公差为\(1\)的等差数列,对我们枚举到的两个相邻位置\(i\)和\(j\),在这段内是不会产生逆序对的,只需要统计前缀的影响
记\(t_i\)表示值域上值为\(i\)的下标数量
求\(\sum_{p=2*s_i-j}^{2*s_i-i}{\sum_{q=-INF}^{p=-1}{t_q}}\)
修改的时候加上一段等差数列,所以再对\(t\)再进行一次差分,直接套\(3\)阶前缀和就行了
时间复杂度为\(O(n\space log\space n)\)轻松过
#include"bits/stdc++.h"
using namespace std;
const int N=500010,M=10;
#define inl inline
#define reg register
#define regi register int
#define PII pair<int,int>
#define ll long long
inl ll read(void)
{
ll x=0,f=1;char ch=getchar();
while(!isdigit(ch)) f=ch=='-'?-1:f,ch=getchar();
while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
return x*f;
}
vector<ll> v[N];
ll sum[N<<1],n,a[N];
int main(void)
{
n=read();scanf("%*d");
int p=sqrt(n);
for(int i=1;i<=n;i++) a[i]=read(),v[a[i]].push_back(i);
ll res=0;
for(int i=0;i<n;i++)
{
if(v[i].size()>p)
{
fill(sum,sum+(n<<1)+1,0);
ll t=n,x=0;++sum[t];
for(int j=1;j<=n;j++)
{
if(a[j]==i) x+=sum[t++];
else x-=sum[--t];
sum[t]++,res+=x;
}
continue;
}
ll m=v[i].size(),*op=v[i].data();
for(int j=0;j<m;j++)
for(int k=j;k<m;k++)
{
ll l=j?op[j-1]:0,r=k+1<m?op[k+1]-1:n,len=(k-j+1)*2;
ll x=max(l,op[k]-len),y=min(op[j],r-len+1);
if(x>op[j]) continue;
res+=r*(op[j]-max(x,y))-(op[k]-1)*(op[j]-x);
if(x<y) res+=(y-x)*(x+len-1)+(y-x-1)*(y-x)/2;
}
}
printf("%lld",res);
return 0;
}
Lost Cows
题目大意:\(给定排列,已知第i个数前面有a[i]个比它小,还原排列。\)
在线问题,维护一个在值域上的树状数组,查询用二分答案, \(O(n\space log^2 \space n)\),两个字“能过”
#include"bits/stdc++.h"
#define ll long long
using namespace std;
const int N=200010;
ll n,a[N],ans[N];
struct tree_array
{
int t[N];
void add(int p,int x)
{
for(;p<=n;p+=p&-p) t[p]+=x;
}
int ask(int p)
{
int res=0;
for(;p;p^=p&-p) res+=t[p];
return res;
}
}t1;
int main(void)
{
scanf("%d",&n);
t1.add(1,1);
for(int i=2;i<=n;i++)
{
scanf("%d",&a[i]);
t1.add(i,1);
}
for(int i=n;i>=1;i--)
{
int l=1,r=n,b;
while(l<=r)
{
int mid=l+r>>1;
if(t1.ask(mid)>=a[i]+1)
b=mid,r=mid-1;
else l=mid+1;
}
ans[i]=b;
t1.add(b,-1);
}
for(int i=1;i<=n;i++)
printf("%d\n",ans[i]);
return 0;
}
GSS3 - Can you answer these queries III
题目大意:动态维护数组,支持单点修改,以及查询区间最大字段和
线段树的建树构图似乎就是天生解决这样的问题的
#include"bits/stdc++.h"
using namespace std;
#define lson rt<<1
#define rson rt<<1|1
using namespace std;
const int N=5e4+10;
int n,m,a[N];
struct Tree
{
int prel,prer,res,sum;
}seg[N<<2];
void pushup(int rt)
{
Tree L=seg[lson],R=seg[rson];
seg[rt].sum=L.sum+R.sum;
seg[rt].prel=max(L.prel,L.sum+R.prel);
seg[rt].prer=max(R.prer,R.sum+L.prer);
seg[rt].res=max(L.prer+R.prel,max(L.res,R.res));
}
void build(int rt,int l,int r)
{
if(l==r)
{
seg[rt].prel=seg[rt].prer=seg[rt].res=seg[rt].sum=a[l];
return;
}
int mid=(l+r)>>1;
build(lson,l,mid);
build(rson,mid+1,r);
pushup(rt);
}
void modify(int x,int rt,int l,int r,int val)
{
if(l==r)
{
seg[rt].prel=seg[rt].prer=seg[rt].res=seg[rt].sum=val;
return;
}
int mid=(l+r)>>1;
if(x<=mid) modify(x,lson,l,mid,val);
else modify(x,rson,mid+1,r,val);
pushup(rt);
}
Tree query(int x,int y,int rt,int l,int r)
{
if(x<=l&&r<=y) return seg[rt];
int mid=(l+r)>>1;
if(y<=mid) return query(x,y,lson,l,mid);
if(mid<x) return query(x,y,rson,mid+1,r);
Tree L=query(x,mid,lson,l,mid),R=query(mid+1,y,rson,mid+1,r),res;
res.sum=L.sum+R.sum;
res.prel=max(L.prel,L.sum+R.prel);
res.prer=max(R.prer,R.sum+L.prer);
res.res=max(L.prer+R.prel,max(L.res,R.res));
return res;
}
int main(void)
{
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
build(1,1,n);
for(scanf("%d",&m);m--;)
{
int opt,x,y;
scanf("%d%d%d",&opt,&x,&y);
if(opt) printf("%d\n",query(x,y,1,1,n).res);
else modify(x,1,1,n,y);
}
return 0;
}
P10463 Interval GCD
题目大意:维护数列,支持区间修改,以及查询区间GCD
线段树的树上运算需要满足有结合律和分配率
注意到\(gcd(a,b)=gcd(a,a-b)[a≥b]\),并且可以拓展:\(gcd(a_l,a_{l+1},...,a_{r-1},a_r)=gcd(a_l,a_{l-1}-a_l,...,a_r-a_{r-1})\)
维护差分序列的\(gcd\)就好了,注意在差分序列上的修改是单点的
#include"bits/stdc++.h"
using namespace std;
const int N=5e5+10;
#define ll long long
ll a[N];
struct node{ll l,r,sum,_gcd;}tr[N*4];
ll gcd(ll a,ll b)
{
return b ? gcd(b,a%b) : a;
}
void pushup(node &u,node &l,node &r)
{
u.sum=l.sum+r.sum;
u._gcd=gcd(l._gcd,r._gcd);
}
void pushup(int u)
{
pushup(tr[u],tr[u<<1],tr[u<<1|1]);
}
void build(int u,int l,int r)
{
if(l==r)
{
ll b=a[l]-a[l-1];
tr[u]={l,r,b,b};
}
else
{
tr[u]={l,r};
int mid=l+r>>1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
pushup(u);
}
}
void modify(int u,int x,ll v)
{
if(tr[u].l==x&&tr[u].r==x)
{
ll b=tr[u].sum+v;
tr[u]={x,x,b,b};
}
else
{
int mid=tr[u].l+tr[u].r>>1;
if(x<=mid) modify(u<<1,x,v);
else modify(u<<1|1,x,v);
pushup(u);
}
}
node query(int u,int l,int r)
{
if(l<=tr[u].l&&tr[u].r<=r) return tr[u];
int mid=tr[u].l+tr[u].r>>1;
if(r<=mid) return query(u<<1,l,r);
else if(l>mid) return query(u<<1|1,l,r);
else
{
node left=query(u<<1,l,r);
node right=query(u<<1|1,l,r);
node res;
pushup(res,left,right);
return res;
}
}
int n,m;
int main(void)
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
build(1,1,n);
char op[2];
int l,r;
ll d;
while(m--)
{
scanf("%s%d%d",op,&l,&r);
if(*op=='Q')
{
node Al=query(1,1,l),Ar=query(1,l+1,r);
printf("%lld\n",abs(gcd(Al.sum,Ar._gcd)));
}
else
{
scanf("%lld",&d);
modify(1,l,d);
if(r+1<=n) modify(1,r+1,-d);
}
}
return 0;
}
DAY2
数据结构2之线段树拓展
AT_abc292_h
P4198
P5579
P3960
P3605
P3224
P6773
SP3946
P8251
P3302
P9329
P5490
P1972
P2163
P9478
P4314
P8868
P6348
P2824
P4097
[ABC292Ex] Rating Estimator
形式化题意:
给定一个长度为 \(n\) 的序列 \(a_i\),参数 B,询问数 q;
每一次询问会对序列单点修改,你需要输出一个实数:
- 如果不存在某一个前缀平均值不低于 B,则输出整体平均值;
- 否则,输出第一个不低于 B 的前缀平均值。
- 将所有数减去 B,前缀平均值不低于 B 变成前缀和非负,考虑如何维护前缀和;
- 发现只有单点修改,对于前缀和来说,就是进行了一次区间(后缀)加,然后我们需要找到第一次出现的非负数;
- 我们可以用线段树维护区间最大值,然后线段树上二分找到那个前缀。
于是时间复杂度 \(O(qlogn)\),空间 \(O(n)\)
#include<bits/stdc++.h>
#define int long long
using namespace std;
struct tree{
int id,l,r,mx,sum,lazy;
}t[2000010];
int a[500010];
void pushup(int id){
t[id].sum=t[id<<1].sum+t[id<<1|1].sum;
t[id].mx=max(t[id<<1].mx,t[id<<1].sum+t[id<<1|1].mx);
}
void pushdown(int id){
if(t[id].lazy!=0){
t[id<<1].lazy=t[id<<1|1].lazy=t[id].lazy;
t[id<<1].sum=t[id].lazy*(t[id<<1].r-t[id<<1].l+1);
t[id<<1|1].sum=t[id].lazy*(t[id<<1|1].r-t[id<<1|1].l+1);
t[id].lazy=0;
}
}
void build(int id,int l,int r){
t[id].l=l;
t[id].r=r;
t[id].sum=t[id].lazy=t[id].mx=0;
if(l==r){
t[id].sum=a[l];
t[id].mx=a[l];
return;
}
int mid=(l+r)>>1;
build(id<<1,l,mid);
build(id<<1|1,mid+1,r);
pushup(id);
}
void update(int id,int l,int r,int v){
if(l<=t[id].l&&t[id].r<=r){
t[id].sum=v*(t[id].r-t[id].l+1);
t[id].lazy=v;
t[id].mx=v*(t[id].r-t[id].l+1);
return;
}
pushdown(id);
int mid=(t[id].l+t[id].r)>>1;
if(l<=mid) update(id<<1,l,r,v);
if(r>mid) update(id<<1|1,l,r,v);
pushup(id);
}
pair<int,int> query(int id,int l,int r,int sum){
// cout<<id<<" "<<l<<" "<<r<<" "<<sum<<" "<<t[id].sum<<" "<<t[id<<1].mx<<endl;
if(t[id].l==t[id].r){
return {t[id].l,sum+t[id].mx};
}
pushdown(id);
if(sum+t[id<<1].mx>=0){
return query(id<<1,l,r,sum);
}else{
return query(id<<1|1,l,r,sum+t[id<<1].sum);
}
}
signed main(){
int n,b,q;
cin>>n>>b>>q;
for(int i=1;i<=n;i++){
cin>>a[i];
a[i]-=b;
}
build(1,1,n);
while(q--){
int op,x;
cin>>op>>x;
x-=b;
update(1,op,op,x);
// return 0;
pair<int,int> pr=query(1,1,n,0);
// cout<<pr.first<<" "<<pr.second<<endl;
double ans=b+1.000000*pr.second/pr.first;
cout<<fixed<<setprecision(10)<<ans<<endl;
}
}
P1972 [SDOI2009] HH的项链
一句话题意:给定一个序列,多次询问区间$ [l,r]$中有多少种不同的数。
我们设序列中 \(a_i\)上一次出现的位置为 \(pre_i\),如果 \(a_i\) 没有出现过,则 \(pre_i=0\)。不难发现如果一种数在区间中出现多次,只会产生一次贡献。不妨钦定每种数产生贡献的位置是区间中第一次出现的位置,这时可以发现,产生的总贡献即为 \(pre_x≤l−1\) 的个数,反证法易证。
现在问题即为:给定一个序列$ pre$,多次查询区间 \([l,r]\) 中有多少个 \(pre_i≤l−1\)。
我们把每一个 \(pre_i\) 抽象到二维平面的点上,把 \(i\)看作横坐标,\(pre_i\) 看作纵坐标,问题既转化为了经典的二维数点问题,每次询问左下角为 \((l,0)\),右上角为 \((r,l−1)\) 的矩形中有几个点。
注意到这个询问是可差分的,我们可以将询问差分为左下角为 \((0,0)\),右上角为 \((r,l−1)\)的矩形减去左下角为 \((0,0)\),右上角为 \((l−1,l−1)\) 的矩形有几个点,这样方便我们使用扫描线思想。
我们将所有操作按横坐标排序(包括加点操作和查询操作),建立权值线段树,维护每个纵坐标出现个数。从左向右扫,如果遇到加点操作就在其纵坐标相应的线段树位置上加 \(1\),如果遇到查询操作就查询线段树中 \([0,val]\)的个数。
单次操作复杂度 \(O(logn)\),共有 \(n\) 次加点操作和$ 2m$ 次查询操作,总时间复杂度 \(O((n+m)logn)\)。
树状数组写法
#include<iostream>
#include<cstdio>
#include<algorithm>
#define rint register int
#define maxn 1000010
using namespace std;
int n,m;
int a[maxn],ans[maxn];
int vis[maxn],tree[maxn];
struct QUE{
int l;
int r;
int id;
}q[maxn];
inline void read(int &x){
char ch=getchar();int f=1;x=0;
while(!isdigit(ch) && ch^'-') ch=getchar();
if(ch=='-') f=-1,ch=getchar();
while(isdigit(ch)) x=x*10+ch-'0',ch=getchar();
x*=f;
}
inline bool cmp(const QUE &a,const QUE &b){
return a.r<b.r;
}
inline int lowbit(int x){
return x&(-x);
}
void modify(int p,int v){
for(;p<=n;p+=lowbit(p))
tree[p]+=v;
}
int query(int p){
int res=0;
for(;p;p-=lowbit(p))
res+=tree[p];
return res;
}
int main(){
read(n);
for(rint i=1;i<=n;++i) read(a[i]);
read(m);
for(rint i=1;i<=m;++i){
read(q[i].l); read(q[i].r); q[i].id=i;
}
sort(q+1,q+m+1,cmp);
int pow=1;
for(rint i=1;i<=m;++i){
for(rint j=pow;j<=q[i].r;++j){
if(vis[a[j]]) modify(vis[a[j]],-1);
modify(j,1);
vis[a[j]]=j;
}
pow=q[i].r+1;
ans[q[i].id]=query(q[i].r)-query(q[i].l-1);
}
for(rint i=1;i<=m;++i) printf("%d\n",ans[i]);
return 0;
}
P2824 [HEOI2016/TJOI2016] 排序
大意:
给一个n的排列(n<=105),有m(m<=105)个操作:
-
1 l r 表示把[l, r]区间内的数降序排序;
-
0 l r 表示把[l, r]区间内的数升序排序。
最后询问这个序列的第p个位子上的数是多少。
做法:
由于将一个普通序列排序很慢,需要\(nlogn\)的时间,所以我们试着把它转化为对01序列排序。先来考虑一个简单的问题:
如何将一个01序列排序?(\(logn\)的复杂度)
-
对于这个问题,我们使用线段树来维护。查询一段区间内的1的个数记为\(cnt1\),如果是升序,就将这段区间的\([r-cnt1+1, r]\)都更改为1,将\([l, r-cnt1]\)更改为0。降序则将\([l, l+cnt1-1]\)更改为1,将\([l+cnt, r]\)更改为\(0\)。这样我们就成功地把排序转化为了区间查询和区间修改。
接下来我们来说本题的做法:
这是一个离线的做法。首先二分答案mid。我们把原排列中大于等于mid的数都标记为\(1\),小于\(mid\)的都标记为\(0\)。然后对于每个操作我们就将01序列排个序。最后如果第\(p\)个位子仍是\(1\)的话就是可行的。
这个二分成立因为是满足单调性的:可以简单地假设一下,如果你二分的答案是1,那么原序列所有的值都转化为了1,所以最后肯定是true。如果二分一个值成立当且仅当这个位子的值大于等于mid,故如果\(check\)返回\(true\),则\(l = mid+1\),否则\(r = mid-1\)。
#include"bits/stdc++.h"
using namespace std;
const int N=101000;
#define inl inline
#define reg register
#define regi register int
#define PII pair<int,int>
#define ll long long
#define ls now<<1
#define rs now<<1|1
int a[N];
int n,m,q;
struct OP{int opt,l,r;}op[N];
int st[N],val[N],tag[N<<2],tr[N<<2];
inl int read(void)
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) f=ch=='-'?-1:f,ch=getchar();
while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
return x*f;
}
inl void pushup(int now){tr[now]=tr[ls]+tr[rs];}
void build(int l,int r,int now)
{
tag[now]=-1;
if(l==r){
tr[now]=st[l];
return ;
}
int mid=l+r>>1;
build(l,mid,ls); build(mid+1,r,rs);
pushup(now);
}
inline void pushdown(int now,int l,int r)
{
if(tag[now]<0) return ;
tag[ls]=tag[rs]=tag[now];
tr[ls]=tag[now]*l; tr[rs]=tag[now]*r;
tag[now]=-1;
}
void update(int L ,int R ,int val,int l,int r,int now)
{
if(l>R||r<L) return ;
if(l>=L&&r<=R){
tr[now]=val*(r-l+1);
tag[now]=val; return ;
}
int mid=(l+r)>>1;
pushdown(now,mid-l+1,r-mid);
update(L,R,val,l,mid,ls);
update(L,R,val,mid+1,r,rs);
pushup(now);
}
int query(int L, int R,int l,int r,int now)
{
if(l>R||r<L) return 0;
if(l>=L&&r<=R) return tr[now];
int mid=(l+r)>>1;
pushdown(now,mid-l+1,r-mid);
int res=0;
res+=query(L, R, l,mid,ls);
res+=query(L, R, mid+1,r,rs);
return res;
}
bool check(int x)
{
fill(st+1,st+1+n,0);
for(int i=1;i<=n;i++)
if(val[i]>=x) st[i]=1;
build(1,n,1);
for(int i=1;i<=m;i++)
{
int l=op[i].l,r=op[i].r;
int cnt=query(l,r,1,n,1);
if(op[i].opt==0)
{
update(r-cnt+1,r,1,1,n,1);
update(l,r-cnt,0,1,n,1);
}else
{
update(l,l+cnt-1,1,1,n,1);
update(l+cnt,r,0,1,n,1);
}
}
return query(q,q,1,n,1);
}
int main(void)
{
n=read(); m=read();
for(int i=1;i<=n;++i) val[i]=read();
for(int i=1;i<=m;++i)
op[i].opt=read(),op[i].l=read(),op[i].r=read();
q=read();
int l=1,r=n,ans=0;
while(l<=r)
{
int mid=l+r>>1;
if(check(mid)) l=mid+1,ans=mid ;
else r=mid-1;
}
printf("%d\n",ans);
return 0;
}
知识点:李超线段树
支持操作:插入直线/线段,查询单点极值
用线段树对于每个区间维护在\(m=(l+r)/2\)处取值最大的直线的信息
若插入一条线段\(f\),在这条线段完整覆盖的区间内,可能会有最优线段发生改变
若一个被\(f\)完全覆盖的一个区间,若五最优线段,则\(f\)直接成武最优线段
否则,区间中点为\(mid\),我们拿\(f\)与原最优线段\(g\)在\(mid\)处的值作比较
\(一、\)如果新线段\(f\)更优,则将\(f\)和\(g\)交换
\(二、\)考虑在\(mid\)处\(f\)不如\(g\)忧的情况:
\(1.\)若在左端点处\(f\)更优,那么\(f\)和\(g\)必然在左半区间中产生了交点,递归到左儿子中进行插入;
\(2.\)若在右端点处\(f\)更优,那么\(f\)和\(g\)必然在右半区间中产生了交点,递归到右儿子中进行插入;
\(3.\)若在左右端点处\(g\)都更优,那么\(f\)不可能成为答案,不需要继续下传
由于仅有一个交点,所以两边子区间最多会递归一个,时间复杂度\(O(n)\)
查询\(x=k\)答案时,从根走到\([x,x]\)节点记录的所有最优线段在\(x=k\)时取值的答案即为所求,这运用标记永久化的思想
基本EX
\(1.\)如果是插入线段,需要定位到线段横坐标区间在李超树上的拆分出的区间,然后一个个递归下去,时间复杂度\(O(log^2{n})\)
\(2.\)李超树的经典运用是斜率优化
标程(P4097 【模板】李超线段树 / [HEOI2013] Segment)
#include"bits/stdc++.h"
using namespace std;
const double eps=1e-9;
const int N=1e6+15;
struct line
{
double k,b;
}p[N];
int tr[N<<2],n,lastans,cnt;
const int M=39989,M_=1000000000;
#define pdi pair<double,int>
int cmp(double a,double b)
{
if(a-b>eps) return 1;
if(b-a>eps) return -1;
return 0;
}
double Y(int id,int x)
{
return p[id].k*x+p[id].b;
}
void change(int u,int l,int r,int L,int R,int id)
{
int mid=l+r>>1;
if(L<=l&&r<=R)
{
int cm=cmp(Y(id,mid),Y(tr[u],mid));
if(cm==1||(!cm&&id<tr[u])) swap(id,tr[u]);
int cl=cmp(Y(id,l),Y(tr[u],l));
int cr=cmp(Y(id,r),Y(tr[u],r));
if(cl==1||(!cl&&id<tr[u])) change(u<<1,l,mid,L,R,id);
if(cr==1||(!cr&&id<tr[u])) change(u<<1|1,mid+1,r,L,R,id);
return ;
}
if(L<=mid) change(u<<1,l,mid,L,R,id);
if(mid<R) change(u<<1|1,mid+1,r,L,R,id);
}
pdi pmax(pdi a,pdi b)
{
if(cmp(a.first,b.first)==1) return a;
if(cmp(a.first,b.first)==-1) return b;
return a.second<b.second?a:b;
}
pdi query(int u,int l,int r,int x)
{
if(l==r) return {Y(tr[u],x),tr[u]};
int mid=l+r>>1;
pdi t={Y(tr[u],x),tr[u]};
if(x<=mid) return pmax(t,query(u<<1,l,mid,x));
return pmax(t,query(u<<1|1,mid+1,r,x));
}
int main(void)
{
int op,x0,y0,x1,y1,x;
double k,b;
scanf("%d",&n);
while(n--)
{
scanf("%d",&op);
if(op==1)
{
scanf("%d%d%d%d",&x0,&y0,&x1,&y1);
x0=(x0+lastans-1)%M+1;
x1=(x1+lastans-1)%M+1;
y0=(y0+lastans-1)%M_+1;
y1=(y1+lastans-1)%M_+1;
if(x0>x1) swap(x0,x1),swap(y0,y1);
if(x0==x1) k=0,b=max(y0,y1);
else k=1.0*(y1-y0)/(x1-x0),b=y0-k*x0;
p[++cnt]={k,b};
change(1,1,M,x0,x1,cnt);
}
else
{
scanf("%d",&x);
x=(x+lastans-1)%M+1;
lastans=query(1,1,M,x).second;
printf("%d\n",lastans);
}
}
return 0;
}
DAY3
离线分治算法
题目列表:
P5787
P3733
CF1140F
CF576E
CF938G
CF1217
P4219
P3810
P3157
P4169
P4390
CF848C
P2487
P4093
P5979
SP3946
P2617
SP10264
P1527
P7424
P4175
\(1.\)线段树分治
\(2.\)基于时间的分治(CDQ分治)
\(3.\)基于值域的分治(整体二分)
P5787 二分图 /【模板】线段树分治
题目大意:\(n\)个点的图,\(m\)条边,每条边存在时间为\([l,r)\),对从\(1\)到\(k\)的每个时刻判断此时图是否为二分图
像区间覆盖一样把每条边出现时间拆成\(log\space k\)个区间,加入这些区间的桶中,之后遍历线段树,到某个区间时把所有这个区间的边加入,离开时删除。用可撤销并查集实现加边和删边的操作
#include"bits/stdc++.h"
using namespace std;
const int N=200010;
int n,k,m;
#define PII pair<int,int>
#define a first
#define b second
struct MST
{
int l,r;
vector<PII> v;
}tr[N<<2];
struct node
{
int id,sz,fa;
}op[N*2];
void build(int p,int l,int r)
{
tr[p].l=l,tr[p].r=r;
if(l==r) return ;
int mid=l+r>>1;
build(p<<1,l,mid),build(p<<1|1,mid+1,r);
}
int Find(int x)
{
return x==op[x].fa?x:Find(op[x].fa);
}
void add(int rt,int l,int r,int s,int t,int a,int b)
{
if(s<=l&&t>=r) return tr[rt].v.push_back(make_pair(a,b)),void();
if(s>r||t<l) return;
int mid=l+r>>1;
add(rt<<1,l,mid,s,t,a,b),add(rt<<1|1,mid+1,r,s,t,a,b);
}
stack<node> st;
void dfs(int p,int l,int r,bool ans)
{
int now=st.size();
bool ans_=0;
MST &u=tr[p];
if(!u.v.empty())
{
for(int i=0;i<u.v.size();i++)
{
int x=Find(u.v[i].a),y=Find(u.v[i].b);
int x_=Find(u.v[i].a+n),y_=Find(u.v[i].b+n);
if(x!=y_)
{
if(op[x].sz>op[y_].sz) swap(x,y_);
st.push(node{x,op[x].sz,op[x].fa});
st.push(node{y_,op[y_].sz,op[y_].fa});
op[x].fa=y_,op[y_].sz+=op[x].sz;
}
if(x_!=y)
{
if(op[x_].sz>op[y].sz) swap(x_,y);
st.push(node{x_,op[x_].sz,op[x_].fa});
st.push(node{y,op[y].sz,op[y].fa});
op[x_].fa=y,op[y].sz+=op[x_].sz;
}
//union
if(Find(x)==Find(x_)) ans_=1;
if(Find(y)==Find(y_)) ans_=1;
}
}
ans|=ans_;int mid=l+r>>1;
if(l==r) puts(ans?"No":"Yes"); else
{
dfs(p<<1,l,mid,ans),dfs(p<<1|1,mid+1,r,ans);
}
while(st.size()!=now)
op[st.top().id].fa=st.top().fa,op[st.top().id].sz=st.top().sz,st.pop();
}
int main(void)
{
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=m;i++)
{
int x,y,l,r;
scanf("%d%d%d%d",&x,&y,&l,&r);
if(l==r) add(1,1,n,l,r,x,y); else
add(1,1,n,l+1,r,x,y);
}
for(int i=0;i<=n<<1;i++) op[i].fa=i,op[i].sz=1;
dfs(1,1,k,0);
return 0;
}
P3810 【模板】三维偏序(陌上花开)
kd-tree,cdq,bitset,树套树都可以写,这里只给出cdq分治写法
题目大意 :有\(n\)个元素,第\(i\)个元素有\(a_i,b_i,c_i\)三个属性,设\(f(i)\)表示满足\(a_j\le a_i\)且\(b_j\le b_i\)且\(c_j]le c_i\)且\(j\neq i\)的\(j\)的数量,对于\(d\in [0,n)\),求\(f(i)=d\)的数量
cdq分治每次计算前一半对后一半的影响。具体地, 假设三维分别是\(x,y,z\),先按\(x\)排序。分治时每次将前半边、后半边分别按\(y\)排序。虽然现在\(x\)的顺序被打乱了,但是前半边还是都小于后半边的,所以要是只计算前半边对后半边的偏序关系,是不会受到\(x\)的影响的。维护后一半的指针\(i\),前一半的指针\(j\),每次将\(i\)后移一位时,若\(y[j]<=y[i]\)则不断后移\(j\),并不断将\(z[j]\)加入树状数组。然后再查询树状数组中有多少数\(\le z[i]\)。 最后要清空树状数组。
#include"bits/stdc++.h"
using namespace std;
const int N=100010;
int tr[N<<2];
int n,n_,m,kk,ans[N];
struct node
{
int x,y,z,w,ans;
}num[N],a[N];
bool cmpt(const node &x,const node &y)
{
if(x.x == y.x)
{
if(x.y == y.y) return x.z < y.z;
return x.y < y.y;
}
return x.x < y.x;
}
bool cmpd(const node &x,const node &y)
{
if(x.y == y.y)
return x.z < y.z;
return x.y < y.y;
}
struct BIT
{
int tr[N<<1];
#define lowbit(x) x & (- x)
int ask(int i)
{
int ans = 0;
for(;i;i -= lowbit(i)) ans += tr[i];
return ans;
}
void add(int i,int k)
{
for(;i <= kk;i += lowbit(i)) tr[i] += k;
}
}t;
void solve(int l,int r)
{
if(l == r) return ;
int mid = l + r >> 1;
solve(l,mid),solve(mid + 1,r);
sort(num + l,num + mid + 1,cmpd);
sort(num + mid + 1,num + r + 1,cmpd);
int i = mid + 1,j = l;
for(;i <= r;i ++)
{
while(num[j].y <= num[i].y && j <= mid) t.add(num[j].z,num[j].w),j ++;
num[i].ans += t.ask(num[i].z);
}
for(i = l;i < j;i ++)
t.add(num[i].z, - num[i].w);
}
void init()
{
int c=0;
for(int i=1;i<=n_;i++)
{
c++;
if(a[i].x!=a[i+1].x||a[i].y!=a[i+1].y||a[i].z!=a[i+1].z)
num[++n]=a[i],num[n].w=c,c=0;
}
}
int main(void)
{
scanf("%d%d",&n_,&kk);
for(int i=1;i<=n_;i++)
scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z);
sort(a+1,a+1+n_,cmpt);
init();
solve(1,n);
for(int i = 1;i <= n;i ++)
ans[num[i].ans + num[i].w - 1] += num[i].w;
for(int i = 0;i < n_;i ++)
printf("%d\n",ans[i]);
return 0;
}
P3157 [CQOI2011] 动态逆序对
CDQ分治作用就是降维
题目大意:对于序列 \(a\),它的逆序对数定义为集合 $${(i,j)| i<j \wedge a_i > a_j }$$中的元素个数,现在给出 \(1\sim n\) 的一个排列,按照某种顺序依次删除 \(m\) 个元素,你的任务是在每次删除一个元素之前统计整个序列的逆序对数。
离线算法(cdq分治)
我们先找出对答案有贡献的点(i,j)对满足的条件: \(Time_i<Time_j,Val_i<Val_j,Pos_i>Pos_j 或 Time_i<Time_j,Val_i>Val_j,Pos_i<Pos_j\)
那么这个问题就变成了经典的三维偏序问题,可以通过cdq分治来解决。
时间:\(O(nlog2n)\)
空间:\(O(n)\)
#include"bits/stdc++.h"
using namespace std;
#define int long long
const int N=1e5+15;
struct node
{
int m,v,d,id,t;
}qlink[N<<1];
int n,m,num;
int pos[N],a[N],c[N];
int ans[N];
bool cmpd(const node &x,const node &y){return x.d<y.d;}
#define lowbit(x) x&(-x)
void add(int x,int k){for(;x<=n;x+=lowbit(x)) c[x]+=k;}
int query(int x){int res=0;for(;x;x-=lowbit(x)) res+=c[x];return res;}
void solve(int l,int r)
{
if(l==r) return ;
int mid=l+r>>1,
R=l;
solve(l,mid),solve(mid+1,r);
sort(qlink+l,qlink+mid+1,cmpd),sort(qlink+mid+1,qlink+r+1,cmpd);
for(int i=mid+1;i<=r;i++)
{
while(R<=mid&&qlink[R].d<=qlink[i].d) add(qlink[R].v,qlink[R].m),++R;
ans[qlink[i].id]+=qlink[i].m*(query(n)-query(qlink[i].v));
}
for(int i=l;i<R;i++) add(qlink[i].v,-qlink[i].m);
R=mid;
for(int i=r;i>mid;i--)
{
while(R>=l&&qlink[R].d>=qlink[i].d) add(qlink[R].v,qlink[R].m),--R;
ans[qlink[i].id]+=qlink[i].m*query(qlink[i].v-1);
}
for(int i=mid;i>R;i--)
add(qlink[i].v,-qlink[i].m);
}
signed main(void)
{
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++)
scanf("%lld",&a[i]),pos[a[i]]=i,qlink[++num]=(node){1,a[i],i,0,num};
for(int i=1,x;i<=m;i++)
scanf("%lld",&x),qlink[++num]=(node){-1,x,pos[x],i,num};
solve(1,num);
for(int i=1;i<=m;i++) ans[i]+=ans[i-1];
for(int i=0;i<m;i++) printf("%lld\n",ans[i]);
return 0;
}
P4093 [HEOI2016/TJOI2016] 序列
题目大意:
给定一个长度为 \(n\)的序列 \(a\)。
同时这个序列还可能发生变化,每一种变化 \((x\_i,y\_i)\) 对应着 \(a_{x_i}\) 可能变成 \(y_i\)。
不会同时发生两种变化。
需要找出一个最长的子序列,使得这个子序列在任意一种变化下都是不降的。
只需要求出这个子序列的长度即可。
注意:可以不发生任何变化。
记 \(f[i]\)为以第 \(i\) 项结尾的子序列最长长度。
则有转移:\(f[i]=max_{j<i}(f[j])+1\),同时还要满足 \(maxval_j≤a_i\) 和 \(a_j≤minval_i\)。
其中 \(maxval_i\)表示第 \(i\) 项最大能变成的值,\(minval_i\) 表示第 \(i\) 项最小能变成的值。按照项从小到大转移,形成了天然的时间顺序,同时还要满足两个偏序限制。
算上时间顺序,这不就是个三维偏序问题,用 CDQ 分治 + BIT 就能解决。
#include"bits/stdc++.h"
using namespace std;
#define int long long
const int N=1e5+15;
int n,m;
struct node
{
int a,b,c,id;
}q[N],q0[N];
int tr[N],f[N],maxn;
bool cmpa(const node &x,const node &y){return x.a<y.a;}
bool cmpb(const node &x,const node &y){return x.b<y.b;}
int query(int x){int res=0;for(;x;x-=x&(-x)) res=max(res,tr[x]);return res;}
void update(int x,int k){for(;x<=maxn;x+=x&(-x)) tr[x]=k==-1?0:max(tr[x],k);}
void cdq_solve(int l,int r)
{
if(l==r)
return ;
int mid=l+r>>1;
cdq_solve(l,mid);
sort(q+l,q+mid+1,cmpa);sort(q+mid+1,q+r+1,cmpb);
int j=l;
for(int i=mid+1;i<=r;i++)
{
while(j<=mid&&q[j].a<=q[i].b) update(q[j].c,f[q[j].id]),j++;
f[q[i].id]=max(f[q[i].id],query(q[i].a)+1);
}
for(int i=l;i<=mid;i++) update(q[i].c,-1);
for(int i=l;i<=r;i++) q[i]=q0[i];
cdq_solve(mid+1,r);
}
signed main(void)
{
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++)
{
int x;scanf("%lld",&x);
q[i].a=q[i].b=q[i].c=x,q[i].id=i,maxn=max(maxn,x);
}
for(int i=1,x,y;i<=m;i++)
{
scanf("%lld%lld",&x,&y);
q[x].b=min(q[x].b,y),q[x].c=max(q[x].c,y),maxn=max(maxn,q[x].c);
}
for(int i=1;i<=n;i++) f[i]=1,q0[i]=q[i];
cdq_solve(1,n);
int ans=-0x3f;
for(int i=1;i<=n;i++) ans=max(ans,f[i]);
printf("%lld",ans);
return 0;
}
P1527 [国家集训队] 矩阵乘法
题目大意:一个\(n \times n\)的矩阵,离线求子矩阵的第\(k\)小数
有一些题目是需要二分来将$ O(N) $的时间复杂度降到$ O(log_2 N) $的,但是如果题目有多次询问且每次询问我们对其都直接二分,时间复杂度就变得让我们无法接受,甚至上升一个数量级,导致 `TLE`。
这时候我们就会用到整体二分。
整体二分是一个离线算法,它的主体思路就是把多个询问或者修改操作一起解决。因此,这个算法总是在最后才把所有的答案一起进行作答。
一般还需要实现一个重要的函数,来进行二分解决所有的操作。个人习惯上称其为 solve(l, r, L, R)。意思就是操作序列上第 \([l,r]\)个询问的答案已经确定在 [L,R] 的值域范围内。
二分嘛,肯定是要取一个 \(mid=⌊\frac{L+R}2⌋\),判定每一个答案与$ mid$ 的关系。
接着枚举询问操作 \((x_1, y_1, x_2, y_2, k)\),记左上角为 \((x_1, y_1)\) ,右下角为 \((x_2, y_2)\) 的子矩阵中,数值在 \([L, mid]\) 的数的个数为 \(cnt\)。显然,如果 \(cnt_i\ge k_i\),那么 \((x_1, y_1, x_2, y_2, k)\) 的答案在\([L, mid]\) 中;否则\((x_1, y_1, x_2, y_2, k - cnt)\) 的答案就在 $[mid + 1, R] $中。
递归处理,当问题缩小为一个数的时候,即\(l=r\) 我们就得到了一些操作的答案
计算二维前缀和的公式大概为
\[ans=S(a,b)−S(a,v−1)−S(u−1,b)+S(u−1,v−1) \]#include"bits/stdc++.h"
using namespace std;
const int N=1e6+15,M=515;
#define int long long
struct Q
{
int x1,y1,x2,y2,k,id;
}q[N<<1],q1[N<<1],q2[N<<1];
int n,q_;
int tr[M][M],ans[N<<1];
#define lowbit(x) x&(-x)
void add(int x,int y,int k)
{
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=n;j+=lowbit(j))
tr[i][j]+=k;
}
int query(int x,int y)
{
int res=0;
for(int i=x;i;i-=lowbit(i))
for(int j=y;j;j-=lowbit(j))
res+=tr[i][j];
return res;
}
int tot=0;
void solve(int l,int r,int L,int R)
{
if(l>r) return ;
int mid=L+R>>1;
if(L==R)
{
for(int i=l;i<=r;i++)
if(q[i].id!=0) ans[q[i].id]=L;
return ;
}
int len1=0,len2=0;
for(int i=l;i<=r;i++)
{
if(q[i].id==0)
{
if(q[i].k<=mid) add(q[i].x1,q[i].y1,1),q1[++len1]=q[i];
else q2[++len2]=q[i];
}
else
{
Q &op=q[i];
int tmp=query(op.x2,op.y2)-query(op.x1-1,op.y2)-query(op.x2,op.y1-1)+query(op.x1-1,op.y1-1);
if(tmp>=q[i].k) q1[++len1]=op;
else op.k-=tmp,q2[++len2]=op;
}
}
for(int i=1;i<=len1;i++) q[l+i-1]=q1[i];
for(int i=1;i<=len2;i++) q[l+len1+i-1]=q2[i];
for(int i=l;i<=l+len1-1;i++)
if(q[i].id==0&&q[i].k<=mid) add(q[i].x1,q[i].y1,-1);
solve(l,l+len1-1,L,mid);
solve(l+len1,r,mid+1,R);
}
signed main(void)
{
scanf("%lld%lld",&n,&q_);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
int x;scanf("%lld",&x);
q[++tot]=(Q){i,j,0,0,x,0};
}
}
for(int i=1;i<=q_;i++)
{
int x1,x2,y1,y2,k;
scanf("%lld%lld%lld%lld%lld",&x1,&y1,&x2,&y2,&k);
q[++tot]=(Q){x1,y1,x2,y2,k,i};
}
solve(1,tot,INT_MIN,INT_MAX);
for(int i=1;i<=q_;i++) printf("%lld\n",ans[i]);
return 0;
}
P7424 [THUPC2017] 天天爱射击
题目大意:x 轴上有 \(n\) 条线段,依次放入 \(m\) 个点,若第 \(i\) 条线段上有 \(s_i\)个点,这条线段便会消失。问放入第 \(i\) 个点时会消失几条线段。
把子弹看做操作,木板看做询问,也就是对每个木板求最小的区间和大于等于s的时刻。
这个时刻显然是单调的,对于单个木板可以二分答案,那么套上整体二分就好。甚至还能求每个子弹能贯穿多少木板
#include"bits/stdc++.h"
using namespace std;
int n,m;
const int N=1e6+15;
struct Q
{
int l,r,s,id,type;
}q[N],q1[N],q2[N];
int tr[N<<1];
#define lowbit(x) x&(-x)
void add(int x,int k)
{
for(;x<=N;x+=lowbit(x))
tr[x]+=k;
}
int query(int x)
{
int res=0;
for(;x;x-=lowbit(x))
res+=tr[x];
return res;
}
int tot;
int ans[N];
void solve(int l,int r,int L,int R)
{
if(l>r) return ;
if(L==R)
{
for(int i=l;i<=r;i++)
ans[L]+=q[i].type;
return ;
}
int mid=L+R>>1,len1=0,len2=0;
for(int i=l;i<=r;i++)
{
if(q[i].type)
{
int tmp=query(q[i].r)-query(q[i].l-1);
if(tmp>=q[i].s) q1[++len1]=q[i];
else q[i].s-=tmp,q2[++len2]=q[i];
}
else
{
if(q[i].id<=mid) add(q[i].l,1),q1[++len1]=q[i];
else q2[++len2]=q[i];
}
}
for(int i=1;i<=len1;i++) if(!q1[i].type) add(q1[i].l,-1);
for(int i=1;i<=len1;i++) q[l+i-1]=q1[i];
for(int i=1;i<=len2;i++) q[l+len1+i-1]=q2[i];
solve(l,l+len1-1,L,mid),solve(l+len1,r,mid+1,R);
}
int main(void)
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
int x,y,z;scanf("%d%d%d",&x,&y,&z);
q[m+i]=(Q){x,y,z,i,1};
}
for(int i=1,x;i<=m;i++) scanf("%d",&x),q[i]=(Q){x,0,0,i,0};
solve(1,n+m,1,1+m);
for(int i=1;i<=m;i++) printf("%d\n",ans[i]);
return 0;
}
DAY 4 - DAY 5
原本是计划回家后再去写游记的,才不是因为前两天数据结构调红温了,我好ruo,qwq,被小 孩哥爆sha了qwq
数据结构学的像shi的我
DAY4-DAY5 "Cafard"讲的是dp
原本觉得学得垃圾,现在觉得更垃圾了
题目:
P9049
CF1408D
CF1710C
CF1415F
CF1430F
CF1442D
CF1453E
CF1453F
CF1455F
CF1467D
CF1468A
CF1481E
CF1485E
CF1485F
CF1487G
CF1497E2
CF1499E
CF1918D
CF1932F
P3736
AT_abc320_f
AT_agc058_b
AT_arc171_c
P5056
P7324
P7519
P10592
AT_arc136_d
AT_agc007_d
AT_abc347_f
AT_abc328_g
ARC037D
うなぎ
Road Trip
元旦老人与汉诺塔
好多qwq,写不完qwq,还是喜欢口胡hah
P9049「PA 2021」Mopadulo
题目大意:划分区间[l,r],求所划分的区间和在mod 1e9+7后为偶数
$解法:设 \sum_i=(\sum_{j=1}^ia_i)\bmod 10^9+7 , dp 数组 f_i那么 f_i 能被 f_j \((j<i) 转移到需要满足以下任意一个条件:
\)sum_j>sum_i 且二者奇偶性不同;\(
\)sum_j≤sum_i 且二者奇偶性相同。\(
\)离散化后用奇偶两个树状数组维护即可。$
GPT3.5写的代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 300005;
const int mod = 1000000007;
int n, m, a[N], sum[N], f[N];
vector<int> lsh;
vector<int> odd, even;
inline int mod_add(int x, int y) {
x += y;
if (x >= mod) x -= mod;
return x;
}
void modify(vector<int>& c, int x, int k) {
while (x <= m) {
c[x] = mod_add(c[x], k);
x += (x & -x);
}
}
int query(const vector<int>& c, int x) {
int res = 0;
while (x > 0) {
res = mod_add(res, c[x]);
x -= (x & -x);
}
return res;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
sum[i] = mod_add(sum[i - 1], a[i]);
}
for (int i = 1; i <= n; i++) {
lsh.push_back(sum[i]);
}
lsh.push_back(0);
sort(lsh.begin(), lsh.end());
lsh.erase(unique(lsh.begin(), lsh.end()), lsh.end());
m = lsh.size();
odd.resize(m + 1);
even.resize(m + 1);
modify(even, 1, 1);
for (int i = 1; i <= n; i++) {
int pos = lower_bound(lsh.begin(), lsh.end(), sum[i]) - lsh.begin() + 1;
if (sum[i] & 1) {
f[i] = mod_add(query(odd, pos), mod_add(query(even, m), mod - query(even, pos - 1)));
modify(odd, pos, f[i]);
} else {
f[i] = mod_add(mod_add(query(odd, m), mod - query(odd, pos - 1)), query(even, pos));
modify(even, pos, f[i]);
}
}
printf("%d\n", f[n]);
return 0;
}
在我多次调教gpt3.5后,终于写出来了HAH
CF1408D Searchlights
题目大意:\(n个强盗(x1,y1)......,m个探照灯(c1,d1).....\)
帮助强盗,别让他们被逮到!!!他们太笨了,只能每回走一步,并且是\(n\)个一起!!!人才
解法:
定义\(f_x\)为向上走\(x\)步,躲开探照灯所需要向右走的最少步数
转移就很简单了
#include"bits/stdc++.h"
using namespace std;
#define int long long
const int N=1e6+10;
int f[N];
struct man
{
int a,b;
}men[N];
struct lig
{
int c,d;
}light[N];
int n,m;
signed main(void)
{
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++) scanf("%lld%lld",&men[i].a,&men[i].b);
for(int i=1;i<=m;i++) scanf("%lld%lld",&light[i].c,&light[i].d);
int limit=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
int a=men[i].a,b=men[i].b,c=light[j].c,d=light[j].d;
if(d<b) continue;
limit=max(d-b,limit);
f[d-b]=max(f[d-b],c-a+1);
}
}
int ans=limit+1;
for(int i=limit,maxn=0;i>=0;i--)
maxn=max(maxn,f[i]),ans=min(i+maxn,ans);
printf("%lld",ans);
return 0;
}
CF1442D Sum
经典的线段树上背包合并
#include"bits/stdc++.h"
using namespace std;
const int N = 3010;
#define inl inline
#define reg register
#define regi register int
#define PII pair<int,int>
#define int long long
using namespace std;
inl int read(void)
{
int x = 0,f = 1;char ch = getchar();
while(!isdigit(ch)) f = ch == '-' ? - 1 : f,ch = getchar();
while(isdigit(ch)) x = (x << 3) + (x << 1) + ch - '0',ch = getchar();
return x * f;
}
int n,k,x,t[N],sum[N],ans,dp[N];
vector<int> a[N];
void solve(int l,int r)
{
int mid = (l + r) >> 1;
if(l == r)
{
int now = 0;
for(int i = 0;i <= min(t[l],k);i ++)
{
ans = max(ans,now + dp[k - i]);
now += a[l][i];
}
return;
}
int f[N];
for(regi i = 0;i <= k;i ++) f[i] = dp[i];
for(regi i = mid + 1;i <= r;i ++)
for(regi j = k;j >= t[i];j --)
dp[j] = max(dp[j],dp[j - t[i]] + sum[i]);
solve(l,mid);
for(regi i = 0;i <= k;i ++) dp[i] = f[i];
for(regi i = l;i <= mid;i ++)
for(regi j = k;j >= t[i];j --)
dp[j] = max(dp[j],dp[j - t[i]] + sum[i]);
solve(mid + 1,r);
}
signed main(void)
{
n = read(),k = read();
for(regi i = 1;i <= n;i ++)
{
t[i] = read();
for(regi j = 1,tmp;j <= t[i];j ++)
{
tmp = read();
a[i].push_back(tmp);
sum[i] += tmp;
}
}
solve(1,n);
printf("%lld",ans);
return 0;
}
CF1453F Even Harder
给定数组 \(a\),\(a_i\) 表示从 \(i\) 能走到 \([i+1, i+a_i]\),问至少需要把几个 \(a_i\) 改成 \(0\),才能使得 \(1\) 到 \(n\) 有且仅有一条路径。
\(设 dp[i,j] ,表示当前那条唯一的链起点为 i ,第二个点为 j 时,最多能保留几个元素。\)
从后往前 dp 容易想到:
\(dp[i,j]=max_{k>i+a_i}{dp[j,k]}+\sum_{i+1≤p≤j−1}[p+a_p≤j−1]+1\)
\(O(n^3)考虑优化\)
\(\text{设}mx[i,j]=max_{j<=k<=n}{dp[i,k]},s[i,j]=\sum_{1≤k≤i}[k+a_k≤j]\)
#include"bits/stdc++.h"
const int N=3010;
using namespace std;
int T,n;
int a[N],f[N][N];
int main(void)
{
cin>>T;
while(T--)
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),a[i]+=i;
for(int i=2;i<=n;i++)
{
int c=0;
for(int j=i;j<=n;j++) f[i][j]=1919810;
for(int j=i-1;j>0;j--)
{
if(a[j]<i) continue;
f[i][a[j]]=min(f[i][a[j]],f[j][i-1]+c);
c++;
}
for(int j=i+1;j<=n;j++) f[i][j]=min(f[i][j],f[i][j-1]);
}
printf("%d\n",f[n][n]);
}
return 0;
}
CF1481E Sorting Books
题目大意:\(n\)本书,每本书有一个颜色\(a_i\),当每种颜色的书都摆在一起时书架上便整齐了,可以每次把一本书放到序列的最有端,问能使书架上整齐的最小操作数
预处理出每种颜色的最左、右位置\(l_i,r_i\),考虑动态规划处理题目的对偶问题,最多能保留几个不移动,令\(dp_i\)为后缀\(suf_i\)即\(a(i,n)\)中能不动书数目的最大值
转移:
考虑到第\(i\)个位置
\(i\) 是这个颜色的左端点,可以把和右端点之间的异色书移走,有转移 \(dp_i←cnt_{a_i}+dp_{r_{a_i}}+1\)。
如果不是 \(cnt_{a_i}\) 为后缀中颜色为 \(a_i\) 的数目。下面就是我要补充的地方。现在有一个方案是保留后缀中颜色为 \(a_i\) 的不动,移动其他的,那么要移动多少?由于 \(i\) 不是右端点,所以后续过程中在 \(i\) 前面且跟 \(i\) 同色的要跟 \(i\) 相邻的话,必须一起移到后面,然后再把 \(suf_i\) 中所有异色的再移出来。所以才有了转移 \(dp_i←cnt_{a_i}\),也就是其它全部移走的意思,这里有一个费用提前计算的思想。
如果要移动当前的书,转移 \(dp_i←dp_{i+1}\)。
由于要移动的最少,那么保留的最多,所有转移取一个最大值
#include"bits/stdc++.h"
using namespace std;
int n;
const int N=5e5+10;
int a[N],cnt[N];
int l[N],r[N];
int f[N];
int main(void)
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
if(!l[a[i]]) l[a[i]]=i;
r[a[i]]=i;
}
for(int i=n;i>=1;i--)
{
f[i]=f[i+1];
cnt[a[i]]++;
if(i!=l[a[i]]) f[i]=max(f[i],cnt[a[i]]);
else f[i]=max(f[i],f[r[a[i]]+1]+cnt[a[i]]);
}
printf("%d",n-f[1]);
return 0;
}
String Journey
题目大意:
对于一个字符串数组 \(t_1, \ldots, t_k\),若对于每一个 \(t_i\) 都是 \(t_{i-1}\) 的真子串的话,即 \(t_i\) 是 \(t_{i - 1}\) 的子串且 \(t_i \ne t_{i-1}\),则称为有序串组,列如 \(\{\mathtt{ab}, \mathtt{b}\}\) 是,\(\{\mathtt{ab}, \mathtt{c}\}\) 和 \(\{ \mathtt{a}, \mathtt{a}\}\) 不是。给定字符串 \(s\),构造有序串组 \(t_1,\ldots,t_k\) 和任意字符串数组 \(u_1,\ldots,u_{k+1}\),使 \(s=u_1+t_1+u_2+t_2 + \cdots +t_k+u_{k+1}\),其中 \(+\) 为字符串的拼接
现在给定一个字符串,求满足条件的最大 \(k\)。
solation:首先发发现答案最大只有\(\sqrt{2n}\),而且串的长度一定是\(ans\),\(ans-1\),...,3,2,1
枚举答案\(ans\),设\(f_i\)为当前答案下以\(i\)开头的后缀是否可行
从后往前枚举,并不断向哈希表中加入长度为\(ans-1\)的不与\([i,i+ans-1]\)重叠的串,转移时查询\([i,i+ans-2]\)或\([i+1,i+ans-1]\)是否出现过即可
每次用到的哈希值长度都为\(ans-1\),所以可以动态维护某个固定长度的哈希值,时间复杂度为\(O(n\sqrt n)\)
#include"bits/stdc++.h"
using namespace std;
const int N=500015;
const int P=7000007,B=37;
#define int long long
int has[N],n,sum,ans;
char ch[N];
bitset<N> f[1015];
int now(int a){return a>=P?a-P:a;}
bitset<P+15> tmp;
inline void solve()
{
ans=sqrt(n<<1)+1,f[1].set(),sum=1;
for(int j=2;j<=ans;j++)
{
sum+=j;
for (int i=n-sum+1;i>=1;i--)
{
int p=i+j;
if(f[j-1][p]) tmp[has[p]]=1;
if(tmp[has[i]]||tmp[has[i+1]]) f[j][i]=1;
}
if(f[j].none()) printf("%lld",j-1),exit(0);
tmp.reset();
for (int i=1;i<=n-sum+1;i++)
has[i]=now((has[i]*B)%P+(ch[j+i-1]-'a'+1));
}
}
signed main(void)
{
scanf("%lld",&n);
cin>>ch+1;
for(int i=1;i<=n;i++) has[i]=ch[i]-'a'+1;
solve();
printf("%lld",ans);
return 0;
}
[AGC002F] Leftmost Ball
题目大意:给你 \(n\) 种颜色的球,每种颜色的球有 \(k\) 个,把这 \(n \times k\) 个球排成一排,把每一种颜色的最左边出现的球涂成白色(初始球不包含白色),求有多少种不同的颜色序列,答案对 \(10^9+7\) 取模
设\(f[i][j]\)表示当前有\(i\)个白球,一共放完了\(j\)种球 显然有\(j <= i\) 对于每个状态目前已经放下去的球是固定了的,那么考虑转移
- 放白球 从\(f[i - 1][j]\)转移
- 放没有出现过的球 \((n - j + 1) * f[i][j - 1] * C(k - 2, n * k - i - (j - 1) * (k - 1) - 1)\)
第二种的C是钦定第一个球放在已经构造好了的合法序列的后面第一个空位,然后剩下的\(k-2\)个球放在剩下的\(n * k - i - (j - 1) * (k - 1) - 1\)空位上。
#include"bits/stdc++.h"
using namespace std;
#define int long long
const int N = 2005, mod = 1e9 + 7;
int f[N][N], n, k;
int fac[N * N], inv[N * N];
int pow(int x, int p)
{
int res = 1;
while(p)
{
if(p & 1) res = res * x % mod;
p >>= 1, x = x * x % mod;
}
return res;
}
int C(int t, int m)
{
if(t < m || t < 0 || m < 0) return 0;
return ((fac[t] * inv[m]) % mod * inv[t - m]) % mod;
}
signed main(void)
{
scanf("%lld%lld", &n, &k);
if(k == 1) return puts("1"), 0;
fac[0] = 1;
for(int i = 1;i <= n * k; i ++) fac[i] = fac[i - 1] * i % mod;
inv[n * k] = pow(fac[n * k], mod - 2);
for(int i = n * k - 1;i >= 1;i --) inv[i] = inv[i + 1] * (i + 1) % mod;
f[0][0] = 1, inv[0] = 1;
for(int i = 1;i <= n;i ++)
for(int j = 0;j <= i;j ++)
{
if(j <= i - 1) f[i][j] = (f[i][j] + f[i - 1][j]) % mod;
if(j) f[i][j] = (f[i][j] + C(n * k - (j - 1) * (k - 1) - i - 1, k - 2) * f[i][j - 1] % mod) % mod;
}
return printf("%lld", fac[n] * f[n][n] % mod), 0;
}
DAY6-DAY8 图论
题目列表:
P2865
P4568
P2149
P4001
CF605E
CF786B
P2294
P2474
P7515
ARC117F
P3403
P2371
P2662
CF1468J
P4180
ARC093E
P3639
「JOI Open 2019」病毒实验
CF888G
CodeChef DDIMMST
P4768
P7834
CF1416D
CF1797F
CF266D
BZOJ2180
P1525
P2024
P3627
P2272
P5025
ARC092F
P4171
UVA11294
P6378
P2860
P7924
P5058
P3469
P3225
CF555E
P3687
P4320
P4630
P1341
P3520
P6628
P3701
P2472
P2754
U64970
CF1592F2
UVA1194
POJ2226
POJ3020
P3355
P2423
UVA1660
P2057
P4313
P2805
P2045
P2053
P1251
P4843
P4553
CF1416F
P2057
P4313
P2805
P2045
P2053
P1251
P4843
P4553
CF1416F
poj等一些题luogu没有
P4001 [ICPC-Beijing 2006] 狼抓兔子
题目描述
现在小朋友们最喜欢的"喜羊羊与灰太狼"。话说灰太狼抓羊不到,但抓兔子还是比较在行的,而且现在的兔子还比较笨,它们只有两个窝,现在你做为狼王,面对下面这样一个网格的地形:
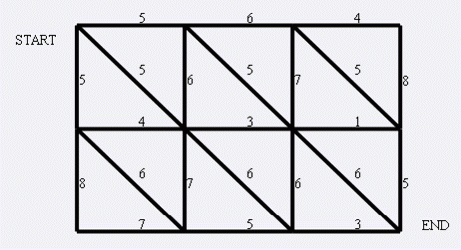
左上角点为 \((1,1)\),右下角点为 \((N,M)\)(上图中 \(N=3\),\(M=4\))。有以下三种类型的道路:
- \((x,y)\rightleftharpoons(x+1,y)\)
- \((x,y)\rightleftharpoons(x,y+1)\)
- \((x,y)\rightleftharpoons(x+1,y+1)\)
求如何才能把羊围起来
解法:
这道题原本是一道最小割的问题,但是写最短路也是一种十分优秀的解法
羊是从\(start\)到\(end\),把每一块分成两个三角,截断羊的活路就是从左下半区到右上半区到最短路
看图,这道题建图需要稍微多斟酌一下
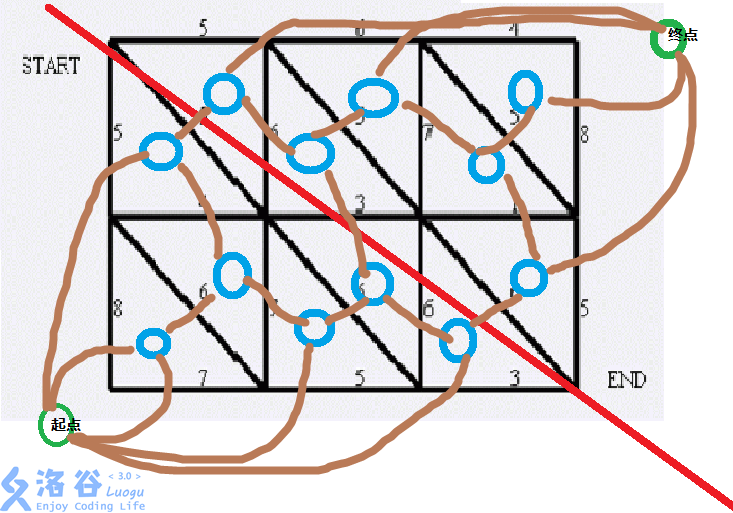
#include"bits/stdc++.h"
using namespace std;
const int N=101000,M=9000010,INF=0x3f3f3f3f;
int head[M],ver[M],tot,net[M];
int dis[M];
int w[M];
void addedge(int u,int v,int c)
{
ver[++tot]=v,net[tot]=head[u],w[tot]=c,head[u]=tot;
}
int n,m;
int T;
bool vis[N];
int dist[N];
struct node
{
int w, now;
bool operator<(const node x) const
{
return w > x.w;
}
};
priority_queue<node> q;
void dijkstra(int s)
{
memset(dis,INF,sizeof dis);
dis[s] = 0; //初始化
q.push(node{0, 0});
while (!q.empty()) //如果堆栈为空,那么所有点都已经更新
{
node x = q.top();
q.pop();
int u = x.now; //记录堆顶并将其弹出
if (vis[u])
continue;
vis[u] = 1;
for (int i = head[u]; i; i = net[i]) //搜索堆顶所有的连边
{
int v = ver[i];
if (dis[v] > dis[u] + w[i])
{
dis[v] = dis[u] + w[i]; //松弛操作
q.push((node){dis[v], v}); //把新遍历的到的点加入堆中
}
}
}
}
int main(void)
{
scanf("%d%d",&n,&m);
if(n==300&&m==600) puts("23611"),exit(0);//打表,打答案,不想调了
T=(2*n-2)*(m-1)+1;
int temp,t1,t2,start=0;
for(int i=1;i<m;i++) scanf("%d",&temp),addedge(i*2,T,temp);
for(int i=2;i<n;i++)
for(int j=1;j<m;j++)
{
scanf("%d",&temp);
t1=2*(i-2)*(m-1)-1+2*j;
t2=2*(i-1)*(m-1)+2*j;
addedge(t1,t2,temp);
addedge(t2,t1,temp);
}
for(int i=1;i<m;i++)
{
scanf("%d",&temp);
t1=2*(n-2)*(m-1)-1+2*i;
addedge(start,t1,temp);
}
for(int i=1;i<n;i++)
for(int j=1;j<=m;j++)
{
scanf("%d",&temp);
t1=2*(i-1)*(m-1)-1+2*j;
t2=t1-1;
if(j==1) addedge(start,t1,temp);
else if(j==m) addedge(t2,T,temp);
else
{
addedge(t1,t2,temp);
addedge(t2,t1,temp);
}
}
for(int i=1;i<n;i++)
for(int j=1;j<m;j++)
{
t1=2*(i-1)*(m-1)-1+2*j;
t2=t1+1;
scanf("%d",&temp);
addedge(t1,t2,temp);
addedge(t2,t1,temp);
}
dijkstra(0);
printf("%d",dis[T]);
return 0;
}
CF786B Legacy
题目大意:有 $n \(个点、\)q $次操作。每一种操作为以下三种类型中的一种:
-
操作一:连一条 $u→v $的有向边,权值为 w。
-
操作二:对于所有$ i ∈ [l,r] \(连一条\) u→i $的有向边,权值为 \(w\)。
-
操作三:对于所有$ i∈[l,r]$ 连一条$ i→u $的有向边,权值为 \(w\)。
求从点$ s $到其他点的最短路。\(1≤n,q≤105,1≤w≤109\)。
**解法: ** 线段树优化建图
建一个出树,和一个入树,以便从属关系处理,例:从\(8\)号点向区间连接一条权值为\(w\)的有向边
使用了\(windows鼠标绘图\),画完一头雾水,这是啥?????
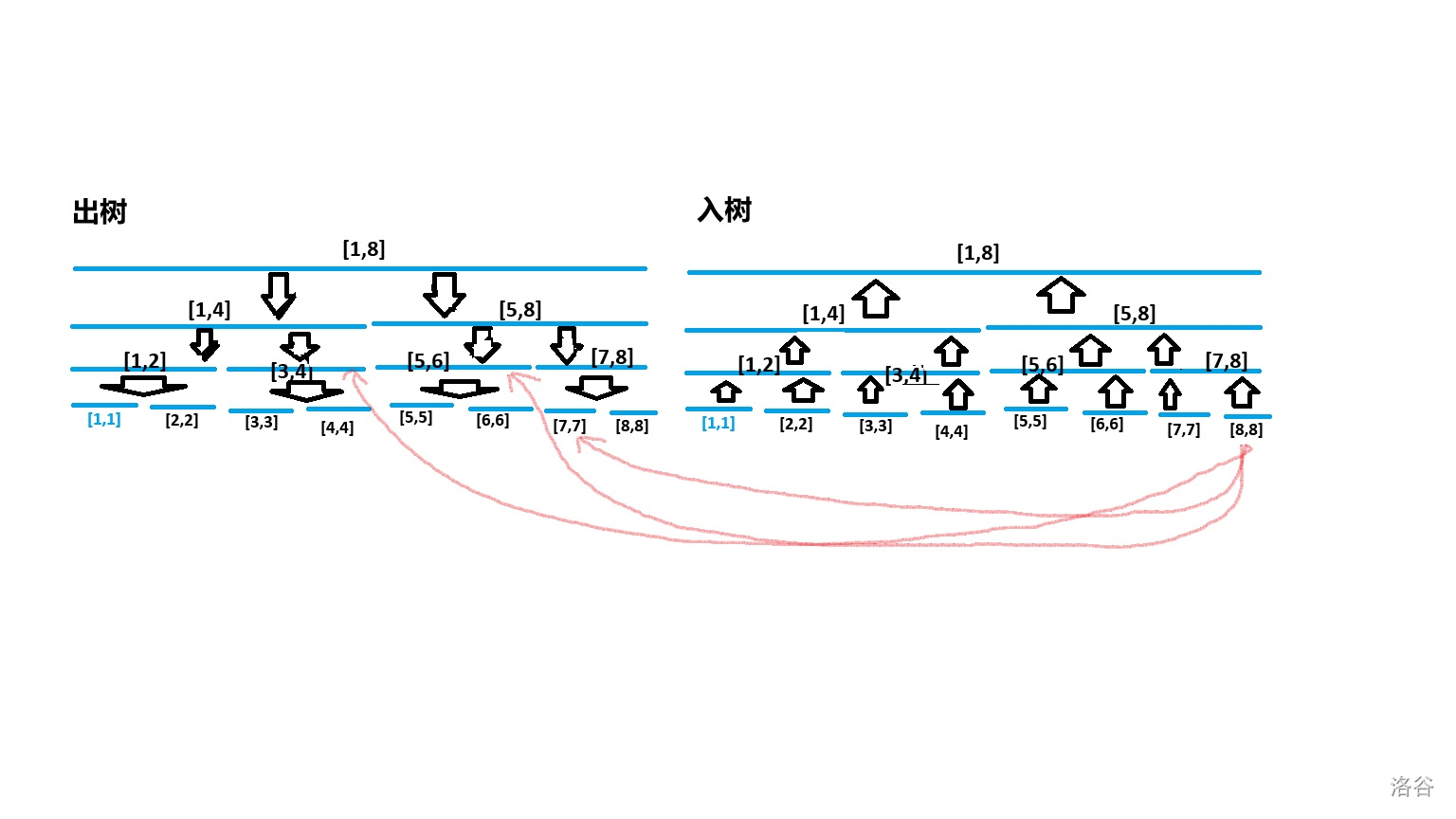
由此建图后,跑一个\(dijkstra\)就可以得出结果了
#include"bits/stdc++.h"
using namespace std;
const int N=3e6+15,M=5e5;
#define int long long
int head[N],ver[N],w[N],net[N],tot,a[N];
int n,m,opt;
int s;
#define PII pair<int,int>
priority_queue<PII> q;
int d[N];
bool vis[N];
int read(void)
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) f=ch=='-'?-1:f,ch=getchar();
while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
return x*f;
}
void addedge(int u,int v,int w_)
{
ver[++tot]=v,net[tot]=head[u],w[tot]=w_,head[u]=tot;
}
struct node
{
int l,r;
int s;
}tr[N];
void build(int p,int l,int r)
{
tr[p].l=l,tr[p].r=r;
if(l==r)
{
a[l]=p;
return ;
}
int mid=l+r>>1;
addedge(p,p<<1,0),addedge(p,p<<1|1,0);
addedge((p<<1)+M,p+M,0),addedge((p<<1|1)+M,p+M,0);
build(p<<1,l,mid),build(p<<1|1,mid+1,r);
}
void modify(int p,int l,int r,int v,int w_)
{
if(l<=tr[p].l&&r>=tr[p].r)
{
if(opt==2) addedge(v+M,p,w_);
else addedge(p+M,v,w_);
return ;
}
int mid=tr[p].l+tr[p].r>>1;
if(l<=mid) modify(p<<1,l,r,v,w_);
if(r>mid) modify(p<<1|1,l,r,v,w_);
}
void dijkstra(int s)
{
memset(d,0x3f,sizeof d);
d[s]=0;
q.push(make_pair(0,s));
while(!q.empty())
{
int x=q.top().second;q.pop();
if(vis[x]) continue;
vis[x]=1;
for(int i=head[x];i;i=net[i])
{
int y=ver[i],z=w[i];
if(d[y]>d[x]+z) d[y]=d[x]+z,q.push(make_pair(-d[y],y));
}
}
}
signed main(void)
{
n=read(),m=read(),s=read();
build(1,1,n);
for(int i=1;i<=n;i++)
addedge(a[i],a[i]+M,0),addedge(a[i]+M,a[i],0);
for(int i=1;i<=m;i++)
{
opt=read();
if(opt==1)
{
int x=read(),y=read(),z=read();
addedge(a[x]+M,a[y],z);
}else
{
int x=read(),l=read(),r=read(),w_=read();
modify(1,l,r,a[x],w_);
}
}
dijkstra(a[s]+M);
for(int i=1;i<=n;i++) printf("%lld%c",d[a[i]]!=0x3f3f3f3f3f3f3f3fll?d[a[i]]:-1,i==n?'\n':' ');//特判
return 0;
}
P7515 [省选联考 2021 A 卷] 矩阵游戏
题目大意:
有一个 \(n\times m\) 的矩阵 \(A\),给出一个 \((n-1)\times(m-1)\) 矩阵 \(B\),满足:
\(b_{i,j} = a_{i,j}+a_{i+1,j}+a_{i,j+1}+a_{i+1,j+1}\)
问你是否存在 \(A\) 满足所有的 \(0\le a_{i,j} \le 10^6\)。
解法
考虑没有限制的时候怎么做?
显然,解法千千万,不再赘述。
先求出一组解(不一定合法),然后再进行调整。
我们发现对于每一行(列),分别加$ +1,−1,+1,−1$显然还一组解。
那么对于第 \(i\) 行,分别加$ +a_i,−a_i,+a_i,−a_i$仍然是一组解。
同理,对于第 \(i\) 列,分别加$ +b_i,−b_i,+b_i,−b_i$也是一组解。
显然,做完这些操作之后每一个数都必须大于等于 000 且小于等于 10610^6106,但我们发现这样子转化成差分约束模型之后,这里并不是真正的差分约束模型,因为全是加法……
我们令$ c_i=(−1)^ia_i, d_i=(−1)^{i+1}b_i\(,再根据\) c,d$ 去搞差分约束,这样子就成功的转化成了差分约束算法。
#include<bits/stdc++.h>
using namespace std;
#define inl inline
#define reg register
#define int long long
using namespace std;
const int N=655,M=1e7+15;
int read(void)
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) f=ch=='-'?-1:f,ch=getchar();
while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
return x*f;
}
int n,m;
int a[N][N],b[N][N],c[N],d[N],tot;
int o=1e6,tim[N],dis[N];
queue<int>q;
bool vis[N];
struct node
{
int to,nxt,w;
}p[M];
int fi[N],cnt;
void addedge(int x,int y,int w)
{
p[++cnt]=(node){y,fi[x],w};fi[x]=cnt;
}
bool spfa(void)
{
memset(dis,0,sizeof(dis));
memset(tim,0,sizeof(tim));
for(int i=1;i<=tot;i++) q.push(i),vis[i]=1;
while(!q.empty())
{
int now=q.front();q.pop();
vis[now]=0;
for(int i=fi[now];~i;i=p[i].nxt)
{
int to=p[i].to;
if(dis[to]<dis[now]+p[i].w)
{
dis[to]=dis[now]+p[i].w;
tim[to]++;
if(!vis[to])
vis[to]=1,q.push(to);
if(tim[to]>tot)
return false;
}
}
}
return true;
}
void solve(void)
{
memset(a,0,sizeof(a));tot=0;
memset(fi,-1,sizeof(fi));cnt=-1;
n=read();m=read();
for(int i=1;i<n;i++)
for(int j=1;j<m;j++) b[i][j]=read();
for(int i=n-1;i>=1;i--)
for(int j=m-1;j>=1;j--) a[i][j]=b[i][j]-a[i+1][j+1]-a[i+1][j]-a[i][j+1];
for(int i=1;i<=n;i++) c[i]=++tot;
for(int j=1;j<=m;j++) d[j]=++tot;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if((i+j)&1)
{
addedge(c[i],d[j],a[i][j]-o);
addedge(d[j],c[i],-a[i][j]);
}
else{
addedge(c[i],d[j],-a[i][j]);
addedge(d[j],c[i],a[i][j]-o);
}
}
}
if(!spfa())
{
puts("NO");return;
}
puts("YES");
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
int add=dis[c[i]]-dis[d[j]];
if((i+j)&1) a[i][j]+=add;
else a[i][j]-=add;
printf("%d ",a[i][j]);
}
puts("");
}
}
signed main(void)
{
int T=read();
while(T--) solve();
return 0;
}
P3403 跳楼机
题目大意:
一个人坐电梯,电梯只有四种移动方式:
1.向上移动\(x\)层
2.向上移动\(y\)层
3.向上移动\(z\)层
4.回到第一层
问电梯一共可以去往的楼层数
解法:
同余最短路的例题
设\(d_i\)为能够到达的最低的\(\mod x = i\)的楼层
则有\(i →^y (i+y) \mod x\)和\(i→^z(i+z)\mod x\)
像这样建图后,\(d_i\)就相当于\(1→i\)的最短路,dijkstra
最后统计时,对于\(d_i \le h\),有贡献\(\left \lfloor \frac{h-d_i}{x} \right \rfloor + 1\)
总时间复杂度为\(O(n\log{n})\)
#include"bits/stdc++.h"
using namespace std;
#define inl inline
#define reg register
#define regi register int
#define PII pair<int,int>
const int N=1e6+15,INF=0x3f3f3f3f;
#define int long long
int n,m,s;
int h,x,y,z;
bool vis[N];
int dis[N];
queue<int> q;
void spfa(int start)
{
memset(dis,INF,sizeof dis);
memset(vis,0,sizeof vis);
dis[start]=1;vis[start]=1;
q.push(start);
while(!q.empty())
{
int u=q.front();q.pop();
int j=(u+y)%x;
if(dis[j]>dis[u]+y)
{
dis[j]=dis[u]+y;
if(!vis[j]) q.push(j),vis[j]=1;
}
j=(u+z)%x;
if(dis[j]>dis[u]+z)
{
dis[j]=dis[u]+z;
if(!vis[j]) q.push(j),vis[j]=1;
}
vis[u]=0;
}
}
signed main(void)
{
scanf("%lld%lld%lld%lld",&h,&x,&y,&z);
if(x==1||y==1||z==1) printf("%lld",h),exit(0);
spfa(1);
int ans=0;
for(int i=0;i<x;i++)
if(dis[i]<=h) ans+=(h-dis[i])/x+1;
printf("%lld",ans);
return 0;
}
P6378 [PA2010] Riddle
题目大意:
\(n\) 个点 \(m\) 条边的无向图被分成 \(k\) 个部分。每个部分包含一些点。
请选择一些关键点,使得每个部分恰有一个关键点,且每条边至少有一个端点是关键点。
解法:
一道$2-sat \(的优化建图,我乃黄金盗图王
从这样的\)O(n^2)\(建图

优化成为这样的\)O(n \log {n})$的建图
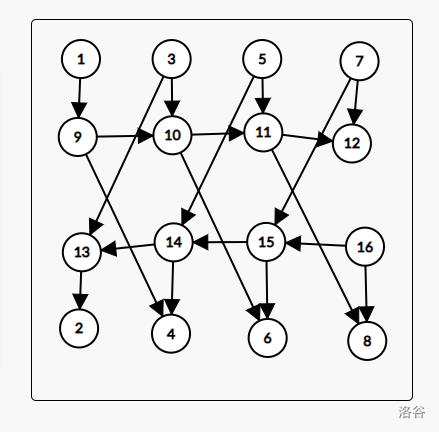
建完图,跑\(2-sat\)就行了,不多解释
#include"bits/stdc++.h"
using namespace std;
const int M=2e7+15,N=2e6+15;
#define inl inline
#define reg register
#define int long long
int scc_id[N<<1],scc_cnt;
int dfn[N<<1],low[N<<1],dfn_cnt;
int sta[N<<1],top;
bool insta[N<<1];
int head[N<<1],ver[M<<1],net[M<<1],cnt;
inl int read(void)
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) f=ch=='-'?-1:f,ch=getchar();
while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
return x*f;
}
inl void addedge(int u,int v)
{
ver[++cnt]=v,net[cnt]=head[u],head[u]=cnt;
}
int n,m,k;
int pre[N<<1][2];
void tarjan(const int &u)
{
low[u]=dfn[u]=++dfn_cnt;
sta[top++]=u;
insta[u]=1;
for(int i=head[u];i;i=net[i])
{
if(!dfn[ver[i]])
{
tarjan(ver[i]);
low[u]=min(low[u],low[ver[i]]);
}
else
if(insta[ver[i]]) low[u]=min(low[u],dfn[ver[i]]);
}
if(low[u]==dfn[u])
{
++scc_cnt;
while(sta[top]!=u)
{
scc_id[sta[top-1]]=scc_cnt;
insta[sta[top-1]]=0;
top--;
}
}
}
int a[N<<1];
signed main(void)
{
int n,m,k,x,y,t;
scanf("%lld%lld%lld",&n,&m,&k);
for(int i=1;i<=m;i++)
{
scanf("%lld%lld",&x,&y);
addedge((x-1)*2+1,(y-1)*2);
addedge((y-1)*2+1,(x-1)*2);
}
int cntt=2*n;
for(int j=1;j<=k;j++)
{
scanf("%lld",&t);
for(int i=1;i<=t;i++)
{
scanf("%lld",&a[i]);
pre[a[i]][0]=++cntt;
pre[a[i]][1]=++cntt;
addedge((a[i]-1)*2,pre[a[i]][0]);//xuan ze lianchu
addedge(pre[a[i]][1],(a[i]-1)*2+1);//lian dao bu xuan
}
for(int i=2;i<=t;i++)
{
int d1=a[i-1],d2=a[i];
addedge(pre[d1][0],pre[d2][0]);
addedge(pre[d2][1],pre[d1][1]);
addedge(pre[d1][0],(d2-1)*2+1);
addedge((d2-1)*2,pre[d1][1]);
}
}
for(int i=0;i<=cntt;i++)
if(!dfn[i]) tarjan(i);
for(int i=1;i<=n;i++)
if(scc_id[(i-1)*2]==scc_id[(i-1)*2+1]) puts("NIE"),exit(0ll);
puts("TAK");
return 0;
}
P2472 [SCOI2007]蜥蜴
题目大意:
在一个r行c列的网格地图中有一些高度不同的石柱,一些石柱上站着一些蜥蜴,你的任务是让尽量多的蜥蜴逃到边界外。
每行每列中相邻石柱的距离为1,蜥蜴的跳跃距离是d,即蜥蜴可以跳到平面距离不超过d的任何一个石柱上。石柱都不稳定,每次当蜥蜴跳跃时,所离开的石柱高度减1(如果仍然落在地图内部,则到达的石柱高度不变),如果该石柱原来高度为1,则蜥蜴离开后消失。以后其他蜥蜴不能落脚。任何时刻不能有两只蜥蜴在同一个石柱上。
解法:
将每个石柱拆成两个点,两点之间的容量为石柱高度\(h\),限制一个石柱只能跳\(h\)次
所有蜥蜴所在的石柱向回点连边,容量为\(1\),向距离内的石柱连一条容量为\(INF\)的边
跑\(dinic最大流\)就行了
#include"bits/stdc++.h"
using namespace std;
const int N = 1015, M = 400015;
const int inf = 1e9;
#define int long long
int n, m, d, cnt, all, s, t;
char str[30];
int head[N], vis[N];
struct edge{
int to, nxt, c;
edge() {}
edge(int x, int y, int z) { to = x, nxt = y, c = z; }
}e[M];
#define id1(x,y) (x-1)*m+y
#define id2(x,y) (x-1)*m+y+n*m
#define dis(x1,y1,x2,y2) (x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)
void addedge(int x, int y, int z)
{
e[cnt] = edge(y, head[x], z); head[x] = cnt ++;
e[cnt] = edge(x, head[y], 0); head[y] = cnt ++;
}
bool bfs(void)
{
queue<int> q; q.push(s);
memset(vis, -1, sizeof vis);
vis[s] = 1;
while(!q.empty())
{
int u = q.front(); q.pop();
for(int i = head[u]; i != -1; i = e[i].nxt)
{
int v = e[i].to;
if(e[i].c && vis[v] == -1)
{
vis[v] = vis[u]+1;
q.push(v);
}
}
}
return vis[t] != -1;
}
int dfs(int u, int flow)
{
if(u == t) return flow;
int used = 0, w;
for(int i = head[u]; i != -1; i = e[i].nxt)
{
int v = e[i].to;
if(vis[v] == vis[u]+1 && e[i].c)
{
w = dfs(v, min(flow-used, e[i].c));
e[i].c -= w; e[i^1].c += w; used += w;
if(used == flow) return used;
}
}
if(!used) vis[u] = -1;
return used;
}
int dinic(void)
{
int ret = 0;
while(bfs()) ret += dfs(s, inf);
return ret;
}
signed main(void)
{
scanf("%d%d%d", &n, &m, &d); memset(head, -1, sizeof head);
s = 0, t = n*m*2+1;
for(int i = 1; i <= n; i ++)
{
scanf("%s", str+1);
for(int j = 1; j <= m; j ++) if(str[j]-'0' > 0) addedge(id1(i, j), id2(i, j), str[j]-'0');
}
for(int i = 1; i <= n; i ++)
{
scanf("%s", str+1);
for(int j = 1; j <= m; j ++) if(str[j] == 'L') addedge(s, id1(i, j), 1), all ++;
}
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= m; j ++)
if(i-d < 1 || i+d > n || j-d < 1 || j+d > m) addedge(id2(i, j), t, inf);
for(int x1 = 1; x1 <= n; x1 ++)
for(int y1 = 1; y1 <= m; y1 ++)
for(int x2 = 1; x2 <= n; x2 ++)
for(int y2 = 1; y2 <= m; y2 ++) if(dis(x1, y1, x2, y2) <= d*d) addedge(id2(x1, y1), id1(x2, y2), inf);
printf("%d\n", all - dinic());
return 0;
}
P4313 文理分科
题目大意:
给出\(art\space ,science\space ,same\underline{} art\space ,same\underline {}science\)这四个矩阵,其中对于\(a\)矩阵,每一个\(a_{i,j}\)表示选择\(A\)学科小P能获得的满意值,每个人选文科或理科可以有满意值,几个人同时选文科或理科也可以获得满意值,求满意值的最大值。
解法:
我乃黄金盗图王,题目中只会有两种状态,一种是选择了\(art\),一种是选择了\(science\),故可以这样连边
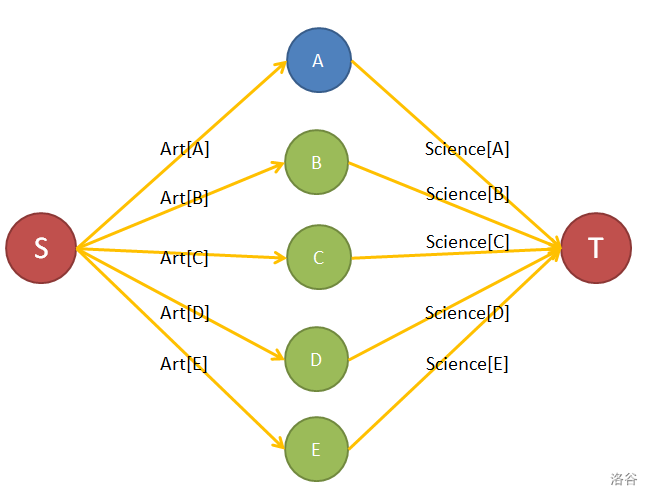
考虑\(same\)与\(a\)的关系,若选择了\(science\)的边,就要把\(same_art\)删掉,同理,若选择了一条\(same\underline{}science\)删掉,加上两个虚点
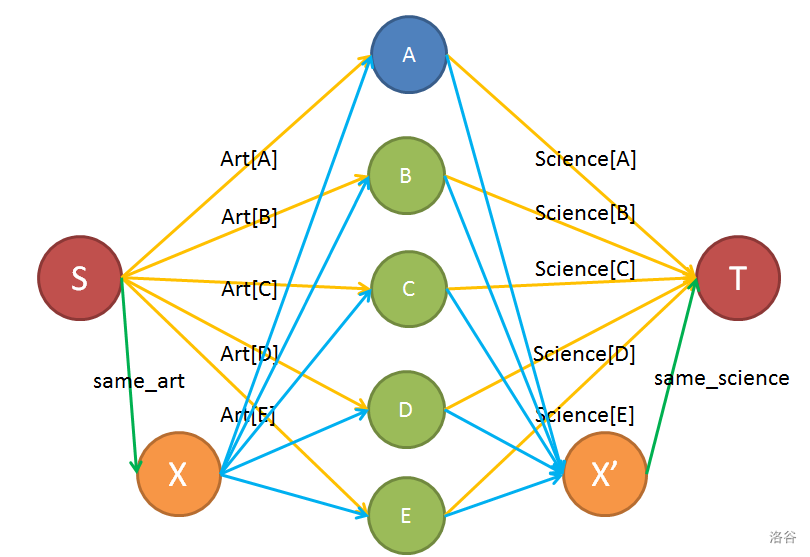
#include"bits/stdc++.h"
using namespace std;
#define int long long
const int N=1e6+15,M=5e3+15,INF=1e18;
int n,m;
int dep[N],head[N],net[N<<1],ver[N<<1],c[N<<1],cnt,cur[N];
void addedge(int a,int b,int flow)
{
ver[++cnt]=b,net[cnt]=head[a],c[cnt]=flow,head[a]=cnt;
}
void add(int a,int b,int flow)
{
addedge(a,b,flow),addedge(b,a,0);
}
int node(int i,int j)
{
return (i-1)*m+j;
}
int ex_art(int i,int j)
{
return n*m+node(i,j);
}
int ex_sci(int i,int j)
{
return n*m*2+node(i,j);
}
bool bfs(int s,int t)
{
memset(dep,-1,sizeof dep);
memcpy(cur,head,sizeof head);
dep[s]=0;queue<int> q;
q.push(s);
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=head[u];i;i=net[i])
{
int ve=ver[i];
if(!c[i]||dep[ve]!=-1) continue;
dep[ve]=dep[u]+1;q.push(ve);
}
}
return dep[t]!=-1;
}
int s,t;
int dfs(int u,int flow)
{
if(u==t) return flow;
int res=0;
for(int &i=cur[u];i;i=net[i])
{
int ve=ver[i];
if(dep[ve]==dep[u]+1&&c[i])
{
int tmp=dfs(ve,min(flow,c[i]));
c[i]-=tmp;c[((i-1)^1)+1]+=tmp;
res+=tmp,flow-=tmp;
}
}
return res;
}
int dinic(void)
{
int res=0;
while(bfs(s,t))
{
int tmp=dfs(s,1e18);
res+=tmp;
}
return res;
}
int mv[5][2]={{1, 0},{-1, 0},{0, 1},{0, -1}};
int art[M][M],sci[M][M],same_art[M][M],same_sci[M][M];
signed main(void)
{
scanf("%lld%lld",&n,&m);
s=n*m*3+1,t=n*m*3+2;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%lld",&art[i][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%lld",&sci[i][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%lld",&same_art[i][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%lld",&same_sci[i][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
add(s,node(i,j),art[i][j]),
add(node(i,j),t,sci[i][j]);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
add(s,ex_art(i,j),same_art[i][j]);
add(ex_sci(i,j),t,same_sci[i][j]);
for(int k=0;k<5;k++)
{
int ti=i+mv[k][0],tj=j+mv[k][1];
if(1<=ti&&ti<=n&&1<=tj&&tj<=m)
add(ex_art(i,j),node(ti,tj),INF),
add(node(ti,tj),ex_sci(i,j),INF);
}
}
}
int ans=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
ans+=art[i][j]+sci[i][j]+same_art[i][j]+same_sci[i][j];
ans-=dinic();
printf("%lld",ans);
return 0;
}
标签:std,20,2024.7,int,void,mid,return,HA,define From: https://www.cnblogs.com/empty-space/p/18397026