标签：int 题单 long times getchar && 动态规划 mod

因为博客园好像标题和网址不能同时用，所以本来点标题就可以跳转了，现在要自己去搜，所以下面附上跳到洛谷的链接。
我的动态规划题单
 我的动态规划题单2

1.CF1620F Bipartite Array

题意等价于:要把这些点分成两部分，每一部分之间都没有边相连，等价于把这个序列中分成两个上升子序列。

在DP时肯定要记录两个序列的末尾，但发现其中一个序列的末尾肯定是 $a[i]$ 或者 $-a[i]$ , 因此只需记录另外一个的。

$f[i][0/1][j]$ 表示把 $a[i]$ 不取反/取反作为一个序列的末尾，另一个序列的末尾是 $j$ 是否可行
由于这个状态值仅仅是可不可行，第三维又很大，于是可以考虑把第三维记录状态:
$f[i][0/1]$ 表示把 $a[i]$ 不取反/取反作为一个序列的末尾，另一个序列的末尾的最小值(显然另一个序列末尾越小越优)。

在转移时看下一个数放在哪个序列末尾，并记录一下方案即可。

写的可能有点麻烦

code

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5,inf=0x3f3f3f3f;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int T,n,a[N],f[N][2],ans[N][2];
bool check(int i,int op){
	if(f[i][op]==inf) return false;
	if(i==1) return true; 
	return check(i-1,ans[i][op]);
}
void print(int i,int op){
	if(i!=1) print(i-1,ans[i][op]);
	if(op==0) printf("%d ",a[i]);
	else printf("%d ",-a[i]);
}
signed main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	T=read();
	while(T--){
		n=read();
		for(int i=1;i<=n;i++) a[i]=read();
		for(int i=1;i<=n;i++) f[i][0]=f[i][1]=inf;
		f[1][0]=f[1][1]=-inf;
		for(int i=2;i<=n;i++){
			//转移f[i][0] 
			if(a[i]>a[i-1]&&f[i-1][0]!=inf){
				if(f[i-1][0]<f[i][0]){
					f[i][0]=min(f[i][0],f[i-1][0]);
					ans[i][0]=0;
				}
			} 
			if(a[i]>f[i-1][0]&&f[i-1][0]!=inf){
				if(a[i-1]<f[i][0]){
					f[i][0]=min(f[i][0],a[i-1]);
					ans[i][0]=0;
				}
			} 
			if(a[i]>-a[i-1]&&f[i-1][1]!=inf){
				if(f[i-1][1]<f[i][0]){
					f[i][0]=min(f[i][0],f[i-1][1]);
					ans[i][0]=1;
				}
			} 
			if(a[i]>f[i-1][1]&&f[i-1][1]!=inf){
				if(-a[i-1]<f[i][0]){
					f[i][0]=min(f[i][0],-a[i-1]);
					ans[i][0]=1;
				}
			} 
			//转移f[i][1] 
			if(-a[i]>a[i-1]&&f[i-1][0]!=inf){
				if(f[i-1][0]<f[i][1]){
					f[i][1]=min(f[i][1],f[i-1][0]);
					ans[i][1]=0;
				}
			} 
			if(-a[i]>f[i-1][0]&&f[i-1][0]!=inf){
				if(a[i-1]<f[i][1]){
					f[i][1]=min(f[i][1],a[i-1]);
					ans[i][1]=0;
				}
			} 
			if(-a[i]>-a[i-1]&&f[i-1][1]!=inf){
				if(f[i-1][1]<f[i][1]){
					f[i][1]=min(f[i][1],f[i-1][1]);
					ans[i][1]=1;
				}
			} 
			if(-a[i]>f[i-1][1]&&f[i-1][1]!=inf){
				if(-a[i-1]<f[i][1]){
					f[i][1]=min(f[i][1],-a[i-1]);
					ans[i][1]=1;
				}
			} 
		}
		if(f[n][0]!=inf||f[n][1]!=inf){
			printf("YES\n");
			if(check(n,1)) print(n,1);
			else print(n,0);
			puts("");
		}
		else puts("NO");
	}
	return 0;
}

2.CF1616H Keep XOR Low

看到位运算，直接就放到 Trie 里面。

一个很自然的想法:设 $f[i]$ 表示第 $i$ 棵子数内的方案数
如果当前考虑到了第 $j$ 位：

如果 $x$ 的第 $j$ 位为 $0$，那显然左右子树不能都选，直接 $f[i]=f[ls]+f[rs]$。
如果 $x$ 的第 $j$ 位为 $1$，这时候就出问题了，因为虽然每棵子树内部可以随便选，但是同时选两棵子树的情况很难转移。

于是大胆一点，设 $f[u][v]$ 表示在 $u$ 子树和 $v$ 子树分别选几个数(可以为空)使他们两两之间满足条件的方案数( $u$ 可以等于 $v$)
注意:对 $u$ 或 $v$ 自身子树里选数没有限制,即只需满足跨子树的限制，可以这样设计是因为当 $u \ne v$ 的时候意味着 $u$ 或 $v$ 这棵子树内的点异或起来的结果在更高的位上已经比 $x$ 小了

如果当前考虑到了第 $j$ 位：

如果 $x$ 的第 $j$ 位为 $1$:
同时选 $u$ 的左儿子和 $v$ 的左儿子显然是一定满足的，同时选右儿子同理
于是只需要把选 $u$ 的左儿子和 $v$ 的右儿子和选 $u$ 的右儿子和 $v$ 的左儿子的方案数乘起来
是乘法原理，因为这两步之间是没有限制的
如果 $x$ 的第 $j$ 位为 $0$:
此时只能同时选 $u$ 的左儿子和 $v$ 的左儿子或同时选右儿子
那就是加法原理，因为这两步如果同时发生会出现既选了 $u$ 的左儿子又选了 $v$ 的右儿子的情况
但注意这里还有一种额外的情况:
因为我们 $f$ 数组的定义只考虑跨界的异或情况，所以我们还可以只选 $u$ 的点或只选 $v$ 的点，要额外加上

每个点只会被遍历一遍，故时间复杂度是对的

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=150000+5,M=6e6+5,mod=998244353;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,x;
int tot=1,ch[M][3],Size[M],mi[M];
void insert(int x){
	int p=1;
	for(int i=30;i>=0;i--){
		int c=(x>>i)&1;
		Size[p]++;
		if(!ch[p][c]) ch[p][c]=++tot;
		p=ch[p][c];
	}
	Size[p]++;
}
int dfs(int u,int v,int d){   //这个计算出的结果可以有空集 
	if(!u) return mi[Size[v]];
	if(!v) return mi[Size[u]];
	if(u==v){
		if(d==-1) return mi[Size[u]];    //到达叶子 
		int ls=ch[u][0],rs=ch[u][1];
		if(x>>d&1) return dfs(ls,rs,d-1);
		else return (dfs(ls,ls,d-1)+dfs(rs,rs,d-1)-1ll+mod)%mod;  //空集会被算两次所以-1 
	}
	if(d==-1) return mi[Size[u]+Size[v]];   
	int ls1=ch[u][0],ls2=ch[v][0],rs1=ch[u][1],rs2=ch[v][1];
	if(x>>d&1) return dfs(ls1,rs2,d-1)*dfs(rs1,ls2,d-1)%mod;
	else{
		int ans=(dfs(ls1,ls2,d-1)+dfs(rs1,rs2,d-1)-1ll+mod)%mod;
		(ans += ( mi[Size[ls1]] - 1ll + mod ) * ( mi[Size[rs1]] -1ll + mod ) )%=mod;
		(ans += ( mi[Size[ls2]] - 1ll + mod ) * ( mi[Size[rs2]] -1ll + mod ) )%=mod;
		  //要减掉左右子树中有一个不选的情况，因为(dfs(ls1,ls2,d-1)+dfs(rs1,rs2,d-1)-1ll+mod)算过了 
		return ans; 
	} 
}
signed main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	n=read(),x=read();
	for(int i=1;i<=n;i++) insert(read());
	mi[0]=1;
	for(int i=1;i<=n;i++) (mi[i]=mi[i-1]*2ll)%=mod;
	printf("%lld\n",(dfs(1,1,30)-1ll+mod)%mod);  //不能是空集 
	return 0;
}

3.CF1775F Laboratory on Pluto

最小周长的图形一定是个凸的图形而不是凹的，否则一定不优。

对于一个凸的图形，他的周长可以通过平移转化成能够包含他的最小矩形的周长,比如:

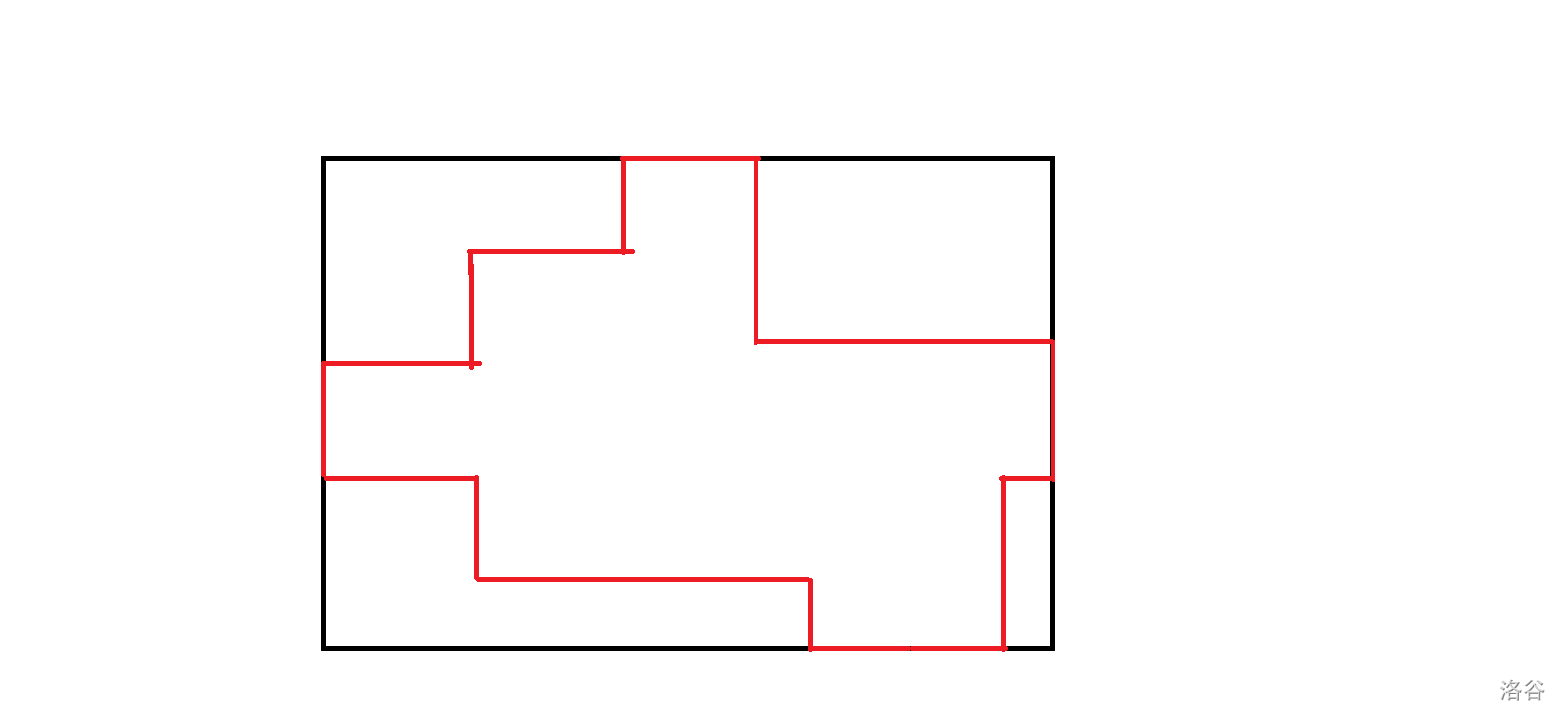
第一问:
假设最小矩形边长为 $a$ , $b$ ，则需满足 $a \times b \ge n$ (因为要往里面填 $n$ 个方块)，在此基础上使 $a+b$ 尽可能小。
假设我们已经确定了 $a\times b$的值，那显然 $a$ , $b$ 越接近，$a+b$越小(小学数学)
具体证明就是$(a+b)^2=(a-b)^2+4ab$....
那肯定 $a$ , $b$ 都取 $\sqrt{n}$ 最优，当然不一定是整数，自己随便凑一凑就可以了.
其实假设 $a<b$ , 则 $ a \le \sqrt{n} $, $O(n \sqrt{n} )$枚举可过，构造方案的话往里面随便填 $n$ 个 # 即可
第二问:
一个凸的图形一定是由那个最小矩形挖去四个角得到的，且挖去的角一定是梯形

先 DP 求出面积为 $i$ 的梯形的方案数，具体来讲:
$g[i][j]$表示面积为$i$,一共有$j$列的梯形的方案数，我们规定梯形每一列的方块数单调不增
那要么新增一列，要么每一列都加一个方块：$g[i][j]=g[i-1][j-1]+g[i-j][j]$
设$sum[i]$表示面积为$i$的梯形的方案数，则 $sum[i]= \sum_{j = 1}^{i} g[i][j]$
因为挖去的方块总数一定不会大于一条边长(否则完全可以缩小矩形)，所以$i,j<=\sqrt{n}$
然后 DP 四个角的情况:
设$f[i][j]$表示挖去$j$个角，一共挖去$i$个方块的方案数，则$f[i][j]=f[i-k][j-1] \times sum[k]$
还是因为挖去的方块总数一定不会大于一条边长，所以四个角一定不会相交。

但是比如当$n=8$时,$2 \times 4$和$3 \times 3$的边长一样是最小的，所以我们这里需要$O(C)$枚举边长,$C$表示周长。
注意这里千万不要$O(n)$枚举边长，因为当$u=2$时没有保证$n \text{的和} \le 8 \times 10^5$

code

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int T,n,u,mod,g[N][N],sum[N],f[N][N]; 
signed main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	T=read(),u=read();
	if(u==1){
		while(T--){
			n=read();
			int a=sqrt(n),b=(n%a==0)?(n/a):(n/a+1);
			printf("%d %d\n",a,b);
			for(int i=1;i<=a;i++){
				for(int j=1;j<=b;j++){
					if((i-1)*b+j<=n) putchar('#');
					else putchar('.');
				}
				puts("");
			}
		}
	}
	else{
		mod=read();
		g[0][0]=1;
		for(int i=1;i<N;i++){
			for(int j=1;j<=i;j++){
				(g[i][j]=g[i-1][j-1]+g[i-j][j])%=mod;
			}
		}
		for(int i=0;i<N;i++){
			for(int j=0;j<=i;j++){
				(sum[i]+=g[i][j])%=mod;
			}
			f[i][1]=sum[i];
		}
		for(int j=2;j<=4;j++){
			for(int i=0;i<N;i++){
				for(int k=0;k<=i;k++){
					(f[i][j]+=1ll*f[i-k][j-1]*sum[k]%mod)%=mod;
				}
			}
		}
		while(T--){
			n=read();
			int a=sqrt(n),b=(n%a==0)?(n/a):(n/a+1),c=a+b,ans=0;
			for(int i=1;i<=c;i++){
				int j=c-i;
				if(i*j>=n) (ans+=f[i*j-n][4])%=mod; 
			}
			printf("%d %d\n",c*2,ans);
		}
	}
	return 0;
}

4.AT_agc002_f [AGC002F] Leftmost Ball

因为每一种球有个数限定，为了避免麻烦,我们在每一次放一种颜色的球时选择把所有对应颜色的球都放进去,具体来讲:
设 $f[i][j]$ 表示目前放了 $i$ 个白球和 $j$ 种颜色的球的方案数
一种合法的方案一定满足对于任意一个前缀白球数量大于等于放的颜色种类,即 $i \ge j$
对于当前放球的状态，我们找到第一个没有被放球的位置(空位和非空位可能交替出现):

如果放白球那就转移到 $f[i+1][j]$
注意放白球的时候我们并不把颜色种类$j+1$
如果选择放不是白色的球 (此时需满足$i>j$)
我们已经放了 $j$ 种，还剩 $n-j$ 种可以放的颜色球，除去那个白色的球和一定要放在这个位置上的球，每种球剩余$k-2$ ,要在在剩余 $ n \times k - i - j \times (k-1) - 1$ 个位置里选出 $k-2$ 个
则用 $f[i][j] \times (n-j) \times C_{n \times k - i - j \times (k-1) - 1}^{k-2}$ 转移到 $f[i][j+1]$

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e3+5,mod=1e9+7,M=4e6+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,k,f[N][N];
int fac[M],inv[M],q[M];
int C(int n,int m){
	return fac[n]*q[m]%mod*q[n-m]%mod;
}
signed main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	n=read(),k=read();
	fac[0]=1;
	for(int i=1;i<M;i++) fac[i]=fac[i-1]*i%mod;
	inv[1]=1;
	for(int i=2;i<M;i++)
		inv[i]=(mod-mod/i)*inv[mod%i]%mod;
	q[0]=1;
	for(int i=1;i<M;i++)
		q[i]=q[i-1]*inv[i]%mod;
	f[1][0]=1;
	for(int i=1;i<=n;i++){
		for(int j=0;j<=i;j++){
			(f[i+1][j]+=f[i][j])%=mod;
			if(i>j) (f[i][j+1]+=f[i][j]*(n-j)%mod*C(n*k-i-j*(k-1)-1,k-2)%mod)%=mod;
		}
	}
	if(k==1) printf("%lld\n",f[n][0]); //特判k=1 
	else printf("%lld\n",f[n][n]);
	return 0;
}

5.CF1615F LEGOndary Grandmaster

先考虑怎么计算两个01串的距离
一个变换:把原串所有偶数位上的数取反，这样$ \text{取反两个原串中相同且相邻的数} = \text{交换两个新串中相邻的数} $
比如原串从001101变成000001，
那么新串就从 011000 -> 010100
并且如果原串中，两个相邻的数不同，那它们在新串中就是相同的，交换他们和没交换一样

所以问题转化成:给定两个01串$S$,$T$ ，求最少的交换次数使得第一个串变成第二个
显然有解的充要条件是$S,T$中$1$的个数相同
设$a_i$表示$S[1,i]$中$1$的个数,$b_i$表示$T[1,i]$中$1$的个数,答案就是 $\sum_{i=1}^{n} |ai-bi|$
证明:
1.首先证明这是个下界，因为最终状态是 $ \sum_{i=1}^{n} |ai-bi| =0 $ 每一次交换 $i$ 和 $i+1$ ，只会影响 $a$ 中 $a_i$ 的值，且 $|ai-bi|$ 的值至多 $-1$ ,所以答案至少是 $\sum_{i=1}^{n} |ai-bi|$
2.可行性:$|ai-bi|$其实计算的就是最终跨过$i$这条分界线进行交换的$1$的个数
${\color{red} {这个结论很重要}}$

然后就是又一个套路:每个位置分别计算贡献
现在$S,T$是题目中的$S,T$了，即有?号
设$f[i][j]$表示使得$a_i-b_i=j$的方案数，$g[i][j]$表示使得$s[i,n]中 $1$ 的个数-t[i,n]中1的个数=j$的方案数这个转移$O(n^2)$很显然所以$ans=\sum_{i=1}^{n} \sum_{j=-n}^{n}f[i][j] \times g[i+1][-j] \times |j|$
因为要满足 $S,T$ 中 $1$ 个数相同
因为下标不可以是负数，所以要偏移量

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e3+5,mod=1e9+7;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int T,n;
string s,t;
int a[N],b[N];
int f[N][N<<1],g[N][N<<1];
signed main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	T=read();
	while(T--){
		n=read();
		cin>>s>>t;
		for(int i=1;i<n;i+=2){
			if(s[i]=='0') s[i]='1';
			else if(s[i]=='1') s[i]='0';
			if(t[i]=='0') t[i]='1';
			else if(t[i]=='1') t[i]='0';
		}
		s=' '+s,t=' '+t;
		for(int i=1;i<=n;i++){
			if(s[i]!='?') a[i]=s[i]-'0';
			if(t[i]!='?') b[i]=t[i]-'0';	
		} 
		for(int i=0;i<=n+1;i++){
			for(int j=0;j<=2*n+2;j++){
				f[i][j]=g[i][j]=0;
			}
		}
		f[0][n]=1;
		for(int i=1;i<=n;i++){
			for(int j=-i;j<=i;j++){
				if(s[i]!='?'&&t[i]!='?') f[i][j+n] = f[i-1][j - (a[i]-b[i]) + n];
				else if(s[i]!='?'&&t[i]=='?') f[i][j+n] = ( f[i-1][j - (a[i]-0) + n] + f[i-1][j - (a[i]-1) + n])%mod;
				else if(s[i]=='?'&&t[i]!='?') f[i][j+n] = ( f[i-1][j - (0-b[i]) + n] + f[i-1][j - (1-b[i]) + n])%mod;
				else f[i][j+n] = ( ( f[i-1][j-1+n] + 2*f[i-1][j+n] ) % mod + f[i-1][j+1+n] )%mod;
			}
		}
		g[n+1][n]=1;
		for(int i=n;i>=1;i--){
			for(int j=-(n-i+1);j<=n-i+1;j++){
				if(s[i]!='?'&&t[i]!='?') g[i][j+n] = g[i+1][j - (a[i]-b[i]) + n];
				else if(s[i]!='?'&&t[i]=='?') g[i][j+n] = ( g[i+1][j - (a[i]-0) + n] + g[i+1][j - (a[i]-1) + n])%mod;
				else if(s[i]=='?'&&t[i]!='?') g[i][j+n] = ( g[i+1][j - (0-b[i]) + n] + g[i+1][j - (1-b[i]) + n])%mod;
				else g[i][j+n] = ( ( g[i+1][j-1+n] + 2*g[i+1][j+n] ) % mod + g[i+1][j+1+n] )%mod;
			}
		}
		int ans=0;
		for(int i=1;i<=n;i++){
			for(int j=-n;j<=n;j++){
				(ans+=f[i][j+n]*g[i+1][-j+n]%mod*abs(j))%=mod;
			} 
		}
		printf("%lld\n",ans);
	}
	return 0;
}

6.CF1430G Yet Another DAG Problem

因为 $B_i>0$ 所以每条边 $u \to v$, $u$ 的权值大于 $v$ 的权值
考虑给图分层，每一层的点的权值相同，层数越大的点点权越小，相邻层的权值差一定是$1$ ,所以 $u$ 的层数一定比 $v$ 小

考虑状压 DP ,假设我们现在把点集 $S$ 放到了前若干层，现在考虑下一层,假设下一层放的点集为$T$,$T$需要满足:

$T \operatorname{and} S=0$,即 $T$ 与 $S$ 无交,相当于 $T$ 是 $S$ 补集的子集
任意一个在 $T$ 中的 $v$,所有指向他的 $u$ 必须都在 $S$ 里 (有了这个限制那也就必然满足所有 $v$ 指向的点都不在 $S$ 中)

考虑转移的代价:
对于每一个在 $S$ 中的 $u$ ,如果 $u \to v$ 的 $v$ 不在 $S$ 中，这条边就会产生贡献
假设 $u$ 在第 $x$ 层，$v$ 在第 $y$ 层，那这条边的贡献应该是 $w_i \times (y-x)$
但是这样不是很好统计，所以我们考虑拆分贡献:
因为 $v$ 至少在下一层，所以每次转移时我们把贡献加上:
$\sum w_i$
即所有满足 $u$ 属于 $S$ , $v$ 不属于 $S$ 的边 $(u,v)$ 的边权
这样的话如果在下一次转移时，这条边的 $v$ 依旧没有被加入进来，那这条边又会产生一次 $w_i$ 的贡献，直到 $v$ 被加入进来，此时刚好产生 $w_i \times (y-x)$ 的贡献
我们对每一个S预处理出:

$\sum wi \text{ (u,v)满足u属于S,v不属于S}$
所有指向 $S$ 中的点的点集
预处理复杂度$O(n \times n \times 2^n)$,DP枚举 $T$ 的时间复杂度 $O(3^n)$

code

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,M=(1<<18)+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,m;
int tot,head[N],to[N],val[N],Next[N];
void add(int u,int v,int w){
	to[++tot]=v,Next[tot]=head[u],val[tot]=w,head[u]=tot;
} 
vector<int> G[N];
int sum[M],ru[M],f[M],from[M],ans[N];
void solve(int s,int val){
	int tmp=s^from[s];
	for(int u=1;u<=n;u++)
		if((s>>(u-1))&1) ans[u]=val;
	if(from[s]) solve(from[s],val+1);
}
void print(int s){
	for(int i=1;i<=n;i++){
		if(s>>(i-1)&1) cout<<i<<' ';
	}
}
signed main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	n=read(),m=read();
	for(int i=1;i<=m;i++){
		int u=read(),v=read(),w=read();
		add(u,v,w);
		G[v].push_back(u);  //记录入边 
	}
	for(int s=0;s<(1<<n);s++){
		for(int u=1;u<=n;u++){
			if((s>>(u-1))&1){
				for(int i=head[u];i;i=Next[i]){
					int v=to[i],w=val[i];
					if(!((s>>(v-1))&1)) sum[s]+=w;
				}
				for(int v:G[u]){
					ru[s]|=(1<<(v-1));
				}
			}
		}
	}
	memset(f,0x3f,sizeof f);
	f[0]=0;
	for(int s=0;s<(1<<n);s++){
		int S=s^((1<<n)-1); //计算补集 
		for(int t=S;t;t=(t-1)&S){ //枚举t 
			if((ru[t]&s)==ru[t]){ //任意一个在T中的v,所有指向他的u必须都在S里
				if(f[s]+sum[s]<f[t|s])
					f[t|s]=f[s]+sum[s],from[t|s]=s;
			}
		}
	} 
	solve((1<<n)-1,0);
	for(int i=1;i<=n;i++) printf("%d ",ans[i]);
	puts("");
	return 0;
}

7.CF1648D Serious Business

用 $pre_{1/2/3}$记录每一行的前缀和
设 $f[x]$ 表示从 $(1,1)$ 到 $(2,x)$ 的最大价值,
则 $ans=\max(f[x]+pre_3[n]-pre_3[x-1])$

考虑每一个操作 $(l_i,r_i,k_i)$ 对 $f[x]$ 的贡献
显然对于每一个 $l_i \le y \le x$ 我都可以按以下路径走: $(1,1) \to (1,y) \to (2,y) \to (2,x)$
即

\[f[x]=max({pre_1[y]+pre_2[x]-pre_2[y-1]-k_i})=max({pre_1[y]-pre_2[y-1]-k_i})+pre_2[x] \]

对于每一个 $l_i-1 \le y \le x$ 我也可以按照以下路径走:
$(1,1) \to (2,y) \to (2,x)$
即

\[f[x]=max({f[y]+pre_2[x]-pre_2[y]-k_i})=max({f[y]-pre_2[y]-k_i})+pre_2[x] \]

注意:这里 $a[2][y]$ 在 $f[y]$ 中算过了，所以是 $pre_2[y]$ ,不是 $pre_2[y-1]$

对于第二个转移还可以精简:
如果 $l_i \le y \le x$ , 那路径必然是:
$(1,1) \to (1,z) \to (2,z) \to (2,y) \to (2,x)$
其中 $1 \le z \le y$

如果 $li \le z \le y$,这条路径
$(1,1) -> (1,z) -> (2,z) -> (2,x)$
在转移1中已经转移过了
如果 $z<l_i$,这条路径再细分:
$(1,1) \to (1,z) \to (2,z) \to (2,l_i-1) \to (2,x)$
而这个其实就是 $f[l_i-1]+pre_2[x]-pre_2[l_i-1-1]-k_i$

所以转移二其实只需要把 $f[x]$ 和 $f[l_i-1]+pre_2[x]-pre_2[l_i-1]-k_i$ 取 $max$

综上得到转移方程为:

\[ f[x]=\max( f[l_i-1] - pre2[l_i-1] - k_i , \max({pre_1[y] - pre_2[y-1] - k_i}) ) + pre_2[x] (l_i \le y \le x) \]

显然可以先转移后半部分，再转移前半部分，并且前半部分的转移可以直接线段树区间取 $max$

现在讨论后半部分的转移
后半部分的转移需满足 $l_i \le y \le x \le r_i$ ，很讨厌，想办法搞掉一个 $r_i$
可以从后往前枚举 $x$ , 并不断加入区间，这样就满足了$r_ i$ 的条件 (但不一定满足 $l_i$ )
线段树上维护三个值 $max_A$ , $max_B$ , $max_{(A+B)}$

$max_A$:表示对应区间上最大的 $-k_i$
$max_B$:表示对应区间上最大的 $pre_1[y] - pre_2[y-1]$
$max_{(A+B)}$:表示对应区间上满足的最大的 $-k_i + pre_1[y] - pre_2[y-1]$ (并且需要满足 $-k_i$ 对应的$l_i$ 在 $pre_1[y] - pre_2[y-1]$ 对应的 $y$ 之前)

于是只要在区间 $[1,x]$ 上查询 $max_{(A+B)}$即可

对于 $-k_i$ 可以在往前扫的时候插入，对于 $pre_1[y] - pre_2[y-1]$ 可以提前就插入
线段树合并时就先合并 $max_A$ 和 $max_B$
对于 $max_{(A+B)}$ : 先继承左右儿子的 $max_{(A+B)}$,再用左儿子的 {max_A} 加上右儿子的 {max_B}

两部分转移各需要一棵线段树

${\color{green} {插一嘴，真的难写}}$

code

#include<bits/stdc++.h>
#define int long long
#define PIII pair<pair<int,int>,int>
#define fi first
#define se second
using namespace std;
const int N=5e5+5,inf=0x3f3f3f3f3f3f3f3f;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,q,a[5][N],pre[5][N],f[N];
struct P{
	int l,r,k;
}b[N];
struct node1{
	int l,r,max_A,max_B,max_sum;
};
struct SegmentTree1{
	node1 t[N<<2];
	void pushup(int p){
		t[p].max_A=max(t[p<<1].max_A,t[p<<1|1].max_A);
		t[p].max_B=max(t[p<<1].max_B,t[p<<1|1].max_B);
		t[p].max_sum=max({t[p<<1].max_sum,t[p<<1|1].max_sum,t[p<<1].max_A+t[p<<1|1].max_B});
	}
	void build(int p,int l,int r){
		t[p].l=l,t[p].r=r;
		if(l==r){
			t[p].max_A=t[p].max_B=t[p].max_sum=-inf;
			return;
		}
		int mid=(t[p].l+t[p].r)>>1;
		build(p<<1,l,mid);
		build(p<<1|1,mid+1,r);
		pushup(p);
	}
	void change_A(int p,int x,int val){
		if(t[p].l==t[p].r){
			t[p].max_A=max(t[p].max_A,val);
			t[p].max_sum=max(t[p].max_sum,t[p].max_A+t[p].max_B);
			return;
		}
		int mid=(t[p].l+t[p].r)>>1;
		if(x<=mid) change_A(p<<1,x,val);
		else change_A(p<<1|1,x,val);
		pushup(p);
	}
	void change_B(int p,int x,int val){
		if(t[p].l==t[p].r){
			t[p].max_B=max(t[p].max_B,val);
			t[p].max_sum=max(t[p].max_sum,t[p].max_A+t[p].max_B);
			return;
		}
		int mid=(t[p].l+t[p].r)>>1;
		if(x<=mid) change_B(p<<1,x,val);
		else change_B(p<<1|1,x,val);
		pushup(p);
	}
	PIII ask(int p,int l,int r){
		if(l<=t[p].l&&t[p].r<=r) return {{t[p].max_A,t[p].max_B},t[p].max_sum};
		int mid=(t[p].l+t[p].r)>>1;
		if(r<=mid) return ask(p<<1,l,r);
		if(l>mid) return ask(p<<1|1,l,r);
		PIII res1=ask(p<<1,l,r),res2=ask(p<<1|1,l,r);
		int max_A=max(res1.fi.fi,res2.fi.fi),max_B=max(res1.fi.se,res2.fi.se),max_sum=max({res1.se,res2.se,res1.fi.fi+res2.fi.se});
		return {{max_A,max_B},max_sum};
	}
}T1;
struct node2{
	int l,r,maxn,lazy;
	void tag(int val){
		maxn=max(maxn,val);
		lazy=max(lazy,val);
	}
};
struct SegmentTree2{
	node2 t[N<<2];
	void pushup(int p){
		t[p].maxn=max(t[p<<1].maxn,t[p<<1|1].maxn);
	}
	void spread(int p){
		if(t[p].lazy!=-inf){
			t[p<<1].tag(t[p].lazy);
			t[p<<1|1].tag(t[p].lazy);
			t[p].lazy=-inf;
		}
	}
	void build(int p,int l,int r){
		t[p].l=l,t[p].r=r,t[p].lazy=-inf;
		if(l==r){
			t[p].maxn=f[l];
			return;
		}
		int mid=(t[p].l+t[p].r)>>1;
		build(p<<1,l,mid);
		build(p<<1|1,mid+1,r);
		pushup(p); 
	}
	void change(int p,int l,int r,int val){
		if(l<=t[p].l&&t[p].r<=r){
			t[p].tag(val);
			return;
		}
		spread(p);
		int mid=(t[p].l+t[p].r)>>1;
		if(l<=mid) change(p<<1,l,r,val);
		if(r>mid) change(p<<1|1,l,r,val);
		pushup(p);
	}
	int ask(int p,int x){
		if(t[p].l==t[p].r) return t[p].maxn;
		spread(p);
		int mid=(t[p].l+t[p].r)>>1;
		if(x<=mid) return ask(p<<1,x);
		else return ask(p<<1|1,x);
	}
}T2;
signed main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	n=read(),q=read();
	for(int i=1;i<=3;i++){
		for(int j=1;j<=n;j++){
			a[i][j]=read();
			pre[i][j]=pre[i][j-1]+a[i][j];
		}
	}
	for(int i=1;i<=q;i++) b[i].l=read(),b[i].r=read(),b[i].k=read();
	
	T1.build(1,1,n);
	for(int i=1;i<=n;i++)
		T1.change_B(1,i,pre[1][i] - pre[2][i-1]);
	sort(b+1,b+q+1,[](const P&x,const P&y){return x.r>y.r;});
	int i=1;
	for(int x=n;x>=1;x--){
		while(i<=q&&b[i].r>=x) T1.change_A(1,b[i].l,-b[i].k),i++;
		f[x]=T1.ask(1,1,x).se; //先别加pre[2][x] 
	}
	
	T2.build(1,1,n);   //建树的时候直接按照f数组 
	
	sort(b+1,b+q+1,[](const P&x,const P&y){return x.l<y.l;});
	for(int i=1;i<=q;i++){
		int l=b[i].l,r=b[i].r;
		if(l>1){
			int tmp=T2.ask(1,l-1);
			T2.change(1,l,r,tmp-b[i].k);
			//注意这个时候因为我们的终点并不是(2,l-1),f[l-1]所以不能加上pre[2][l-1],直接用原来没有加过pre2的f值是对的 
		}
		//这个转移的意义是先走到(2,l-1),所以l!=1 
	}
	for(int i=1;i<=n;i++) f[i]=T2.ask(1,i)+pre[2][i];   
	int ans=-inf;
	for(int i=1;i<=n;i++){
		ans=max(ans,f[i]+pre[3][n]-pre[3][i-1]);
	}
	printf("%lld\n",ans);
	return 0;
}

8.CF367E Sereja and Intervals

一个关于互不包含区间的结论：
如果把区间左端点升序排序，则区间右端点也必然升序
也就是说当你确认了 $n$ 个 $l_i$ ,和 $n$ 个 $r_i$,那他们的组合方法是唯一的.
所以你现在要构造两个序列 {$l_i$},{$r_i$} ,满足：

$1 \le l_1 < l_2 < l_3 < l_4 < l_5 < ...< l_n \le m$
$ 1 \le r_1 < r_2 < r_3 < r_4 < r_5 < ... < r_n<=m $
$l_i \le r_i$
$\text{存在} l_i=x$

考虑几个性质:

不可能存在一个点存在两个左端点/右端点
$n>m$ 时无解，所以可以认为 $n \le m$ , 即 $n \le \sqrt {10^5}$
3限制等价于对于每一个$i$,其左边左端点 $cnt(l,i)$ 的数量 $\ge$ 其左边右端点的数量 $cnt(r,i)$

如果没有限制4,考虑 DP :
$f[i][j][k]$ 表示给前 $i$ 个位置分配 $j$ 个 $l$ 端点,$k$ 个 $r$ 端点的方案数 $(j \ge k)$ 。
转移时，每一个位置你要么分配一个 $l$ ,要么分配一个 $r$ ,要么分配 $l$ , $r$ 各一个，要么啥也不分配
时间复杂度$O(m \times n^2)$

如果有限制4,其实只需要在 $i=x$ 时，强制只转移有放左端点的情况

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e3+5,mod=1e9+7;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,m,x;
int f[2][400][400];   //滚动数组 
signed main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	n=read(),m=read(),x=read();
	if(n>m){
		printf("0\n");
		return 0;
	}
	f[0][0][0]=1;
	for(int i=1;i<=m;i++){
		for(int j=0;j<=min(i,n);j++){
			for(int k=0;k<=j;k++){
				if(j-1>=k&&j-1>=0) (f[i&1][j][k]+=f[1-(i&1)][j-1][k])%=mod;
				if(i!=x&&k-1>=0) (f[i&1][j][k]+=f[1-(i&1)][j][k-1])%=mod;
				if(j-1>=0&&k-1>=0) (f[i&1][j][k]+=f[1-(i&1)][j-1][k-1])%=mod;
				if(i!=x) (f[i&1][j][k]+=f[1-(i&1)][j][k])%=mod;
			}
		}
		for(int j=0;j<=min(n,i);j++){
			for(int k=0;k<=j;k++){
				f[1-(i&1)][j][k]=0;
			}
		}
	}
	int fac=1;
	for(int i=1;i<=n;i++) (fac*=i)%=mod;   //区间有编号所以乘以n! 
	printf("%lld\n",f[m&1][n][n]*fac%mod);
	return 0;
}

9.CF1574F Occurrences

这个限制是真的抽象，而且这题里的子序列指子串，为了避免误会下面直接写子串

考虑转化限制:
仔细想一想可以发现 $A$ 在序列 $a$ 中每出现一次，
其每个子串都会出现一次，且出现次数最多的一定是长度为$1$的单个字符。
所以这个限制其实就是:$A$ 在 $a$ 中出现的次数 $=$ 其每个字符在 $a$ 中出现的次数。

考虑几种情况:

如果$A=\text{123}$,此时当 $a$ 中填了一个 1 时，必定要按照顺讯再填进去 2,3即 $a$ 中要么没有 1 ，有的话一定是以 123 的形式出现的。
如果连边的话会发现此时 $1 \to 2 \to 3$构成一条链。
如果$A=\text{121}$,会发现此时无论如何填1出现的次数一定大于 $A$,除非不填1。
而此时连边会出现环，即有环的一定不能填。
如果$A=\text{123},B=\text{234}$,此时要把 $A$ 和 $B$ 的链合并，变成1234。
如果$A=\text{123},B=\text{124}$,此时出现了分支，同样不能填。

于是一个做法就成型了:

一开始每个数字自成一个连通块。
对每个序列 $A$ ,按照顺序连边。
对每一个连通块，如果它存在环或者存在分支(即它不是链)，那这个连通块内的数都不能出现在 $a$ 中。
否则这条链可以出现在a中
对每一个可以出现的链做一次完全背包,即如果长度为 $j$ 的链有 $w_j$ 个,$f[i]$ 表示构造长度为 $i$ 的 $a$ 的方案数，有$f[i]=\sum_{j=1}^i f[i-j] \times w_j$

这样转移可以大大加快速度，因为枚举每个链可能有 $O(k)$个，但不同的链长一定小于等于 $O(\sqrt {k})$个
因为假设不同链长有 $l$ 个，那即使这些链的长度为$1,2,3,4,...,l$
则 $(1+2+3+..+l)=\frac {(1+l) \times l}{2} \le k$,即$ l \le \sqrt{2k}$

code

#include<bits/stdc++.h>
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=3e5+5,mod=998244353;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,m,k,a[N]; 
map<PII,bool> mp;
int tot,head[N],to[N],Next[N],ru[N],chu[N]; 
void add(int u,int v){
	to[++tot]=v,Next[tot]=head[u],head[u]=tot;
	ru[v]++,chu[u]++;
}
int num,c[N],siz[N];
bool vis[N],flag[N];
void dfs(int u){
	siz[num]++;
	vis[u]=true,c[u]=num;
	for(int i=head[u];i;i=Next[i]){
		int v=to[i];
		if(vis[v]) flag[num]=false;
		else dfs(v);
	}
}
set<int> len;
int w[N],f[N];
signed main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	n=read(),m=read(),k=read();
	memset(flag,true,sizeof flag);
	for(int i=1;i<=n;i++){
		int c=read(),lst;
		for(int j=1;j<=c;j++){
			a[j]=read();
			if(j>1&&!mp[{lst,a[j]}]) add(lst,a[j]),mp[{lst,a[j]}]=true;;
			lst=a[j];
		}
	}
	for(int i=1;i<=k;i++){
		if(!vis[i]&&ru[i]==0) num++,dfs(i);
	}
	for(int i=1;i<=k;i++) 
		if(ru[i]>1||chu[i]>1) flag[c[i]]=false;
	for(int i=1;i<=num;i++)
		if(flag[i]) len.insert(siz[i]),w[siz[i]]++;

	f[0]=1;
	
	for(int i=1;i<=m;i++){
		for(int x:len) if(i>=x) (f[i]+=f[i-x]*w[x])%=mod;
	}
	printf("%lld\n",f[m]);
	return 0;
}

10.P5662 [CSP-J2019] 纪念品

因为当日购买的纪念品也可以当日卖出换回金币。
所以如果想保留一个纪念品可以看成是:

第一天买，第二天早上卖，第二天再买回，第三天早上卖，第三天再买回...

这样就不用管每一天手上有多少纪念品，只需要认为我当天买的第二天一早一定会直接卖掉，啥也不剩，至于再买不买回来是第二天的事。

设 $A_{i,j}$ 表示第 $i$ 天 $j$ 物品的价格。
假设我考虑到了第 $i$ 天，手里剩 $M$ 元 , 买入一个物品需要花 $A_{i,j}$ 元，收益是 $A_{i+1,j} - A_{i,j}$。
可以看成是有一个体积为 $M$ 的背包，每个物品的体积为 $A_{i,j}$ ，价值是 $A_{i+1,j} - A_{i,j}$ 的完全背包
最后按照当天获得的最大价值当做下一天的起始资金即可。

code

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int T,n,M,a[105][105];
int f[N];
signed main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	T=read(),n=read(),M=read();
	for(int i=1;i<=T;i++){
		for(int j=1;j<=n;j++){
			a[i][j]=read();
		}
	}
	for(int i=1;i<T;i++){
		for(int k=0;k<=M;k++) f[k]=0;
		for(int j=1;j<=n;j++){
			for(int k=a[i][j];k<=M;k++){
				f[k]=max(f[k],f[k-a[i][j]]+a[i+1][j]-a[i][j]);
			}
		}
		M=M+f[M];  //因为f数组算的是可以收益多少，所以M直接+f[M] 
	}
	printf("%d\n",M);
	return 0;
}

11.P2886 [USACO07NOV] Cow Relays G

矩阵快速幂优化 DP 板子

我们用一个矩阵表示两两之间的答案,一开始 $A[i][j]$ 表示 $i$ , $j$ 只经过一条边的最短路
把矩阵乘法改成 $C[i][j] = min(A[i][k]+A[k][j])$
这里 k 相当于枚举了中转点 (参考Floyd)
并且此时路径长度会变成2倍，最终要求是 n 倍，做矩阵快速幂即可

code

#include<bits/stdc++.h>
#define int long long 
#define PIII pair<int,pair<int,int> > 
#define fi first
#define se second
using namespace std;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int dis[10005],N,n,m,s,t;
vector<PIII> G;
int Dis(int x){
	return lower_bound(dis+1,dis+n+1,x)-dis;
}

int ans[1005][1005],c[1005][1005];
void mul(int f[1005][1005],int a[1005][1005]){  //矩阵乘法 
	memset(c,0x3f,sizeof c);
	for(int k=1;k<=n;k++){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				c[i][j]=min(c[i][j],f[i][k]+a[k][j]);
			}
		}
	}
	memcpy(f,c,sizeof c);
}
void Quick_power(int a[1005][1005],int b){
	for(int i=1;i<=n;i++){    //单位矩阵 
		for(int j=1;j<=n;j++){
			if(i==j) ans[i][j]=0;
			else ans[i][j]=0x3f3f3f3f3f3f3f3f;
		}
	}
	while(b){
		if(b&1) mul(ans,a);
		b>>=1,mul(a,a);
	} 
	memcpy(a,ans,sizeof ans);
}
int a[1005][1005];
signed main(){
	N=read(),m=read(),s=read(),t=read();
	memset(a,0x3f,sizeof a);
	for(int i=1;i<=m;i++){
		int w=read(),u=read(),v=read();
		G.push_back({u,{v,w}});
		dis[i]=u,dis[i+m]=v;
	}
	sort(dis+1,dis+2*m+1);
	n=unique(dis+1,dis+2*m+1)-dis-1;
	for(PIII x:G){
		int u=x.fi,v=x.se.fi,w=x.se.se;
		u=Dis(u),v=Dis(v);
		a[u][v]=a[v][u]=w;
	}
	
	Quick_power(a,N);
	
	printf("%lld\n",a[Dis(s)][Dis(t)]);
	return 0;
}

12.P6569 [NOI Online #3 提高组] 魔法值

相同的转移情况再次想到矩阵快速幂。

构造转移矩阵 $G$ , 若 $u$,$v$ 之间有边,则 $G[u][v]=1$ , 否则 $G[u][v]=0$
将矩阵乘法改成 $C[i][j] = \operatorname{xor} ^ n _ {k=1} A[i][k] \times B[k][j]$
注意:广义矩乘若要满足结合律必须满足——加法满足交换律，乘法满足结合律，并对加法满足分配率，而普通的异或对加法是没有分配律的，也不能这么改变，但由于这里只有 $0/1$ 所以可以

直接快速幂的总时间复杂度是 $ O(q \times n^3 * \log a)$ 过不了。
所以考虑预处理出 $G^1,G^2,G^4,......$ ,并对 $a$ 进行二进制拆分，这样每一次乘都是一个 $n \times n$矩阵乘以 $1 \times n$的向量，时间复杂度变成 $ O(q \times n^2 * \log a)$

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,m,q; 
struct matrix{
	int x[105][105];
	int n,m;
}f,a,mi[40];
matrix mul(matrix x,matrix y){
	matrix ans;
	ans.n=x.n,ans.m=y.m;
	memset(ans.x,0,sizeof ans.x);
	for(int k=1;k<=x.m;k++){
		for(int i=1;i<=ans.n;i++){
			for(int j=1;j<=ans.m;j++){
				ans.x[i][j]^=(x.x[i][k]*y.x[k][j]);
			}
		}
	}
	
	return ans;
}
signed main(){
	n=read(),m=read(),q=read();
	f.n=1,f.m=n;
	a.n=n,a.m=n;
	for(int i=1;i<=n;i++) f.x[1][i]=read();
	for(int i=1;i<=m;i++){
		int u=read(),v=read();
		a.x[u][v]=a.x[v][u]=1;
	}
	
	mi[0]=a;
	for(int i=1;i<=32;i++) mi[i]=mul(mi[i-1],mi[i-1]);
	
	
	while(q--){
		int t=read();
		matrix ans=f;
		for(int i=0;i<=32;i++){
			if(t>>i&1) ans=mul(ans,mi[i]);
		}
		printf("%lld\n",ans.x[1][1]);
	}
	return 0;
}

13.P6190 [NOI Online #1 入门组] 魔法

一条合法的 $1 \to n$ 路径可以拆成两部分:

一开始没有任何魔法的路径
若干段满足:第一条路径用了魔法，后面没有用的路径

并且如果可以用完一定会把 $k$ 次魔法用完。
所以 $A[i][j]$ 表示 $i$ 到 $j$ 用一次魔法且用在第一条的最短距离。
矩阵快速幂到 $A^k$ 即为用了 $k$ 次魔法。
注意还要用Floyd跑出全源最短路，处理出那些没有任何魔法的路径的最小值。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e5+5,inf=1e15;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,m,k;
void Init(int a[105][105]){
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(i!=j) a[i][j]=inf;   //这里特殊判断 i!=j , 防止 1--n 路径上可能不足 k 条边的情况 
		}
	}
}
int ans[105][105],c[105][105];
void mul(int f[105][105],int a[105][105]){  //矩阵乘法 
	Init(c);
	for(int k=1;k<=n;k++){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				c[i][j]=min(c[i][j],f[i][k]+a[k][j]);	
			}
		}
	}
	memcpy(f,c,sizeof c);
}
void Quick_power(int a[105][105],int b){
	for(int i=1;i<=n;i++){    
		for(int j=1;j<=n;j++){
			if(i==j) ans[i][j]=0;
			else ans[i][j]=inf;
		}
	}
	while(b){
		if(b&1) mul(ans,a);
		b>>=1,mul(a,a);
	} 
	memcpy(a,ans,sizeof ans);
}

int f[105][105],a[105][105]; 
int tot,head[N],to[N],Next[N],val[N];
void add(int u,int v,int w){
	to[++tot]=v,Next[tot]=head[u],val[tot]=w,head[u]=tot;
}
signed main(){
	n=read(),m=read(),k=read();
	
	Init(f);
	for(int i=1;i<=n;i++) f[i][i]=0;
	for(int i=1;i<=m;i++){
		int u=read(),v=read(),w=read();
		f[u][v]=w;
		add(u,v,w);
	}
	for(int k=1;k<=n;k++){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
				
			}
		}
	}
	
	if(k==0){
		printf("%lld\n",f[1][n]);
		return 0;
	}
	
	Init(a);
	for(int u=1;u<=n;u++){
		for(int v=1;v<=n;v++){
			for(int i=head[u];i;i=Next[i]){
				int w=val[i];
				a[u][v]=min(a[u][v],-w+f[to[i]][v]);
			}
		}
	}
	
	Quick_power(a,k);

	int res=inf;
	for(int u=1;u<=n;u++){
		res=min(res,f[1][u]+a[u][n]);
	}
	printf("%lld\n",res);
	return 0;
}

14.P6772 [NOI2020] 美食家

朴素 DP : $f[i][u]$ 表示第 $i$ 天到 $u$ 的最大收益。
则 $f[i][u] = max(f[i-w][v]+c[u])$ (存在一条边 $(v,u,w)$ )

因为 $T$ 很大，考虑矩阵快速幂优化：
由于矩阵快速幂一般只能优化从 $f[i] \to f[i+1]$ 的转移，所以考虑拆点。
Tip:之所以不拆边是因为 n 比较小
即把一个点 $u$ 拆成 $ u_1,u_2,u_3,u_4,u_5$
并且按照 $u_1 \to u_2 \to u_3 \to u_4 \to u_5$ 连边
若存在一条边 $(u,v,3)$ 则按照 $u_3 -> v_1$ 连边
相当于变成新图中经过了多少条边就是几天。
并且只在所有节点分裂出的第一个点，即 $u_1$ 上 $c[ u_1 ]= c[u] $, 其余点的 $c$ 值均为 $0$。

设计转移矩阵 $G$ ，若新图中 $u$ 和 $v$ 之间有边，
则 $G[u][v] = c[v]$,否则 $G[u][v] = -inf$ 。
改变矩乘定义:
$ C[i][j] = \max{A[i][k] + B[k][j]} $。

一开始除了 $f[1][1]=c[1]$ 其余均为 $-inf$。
若不考虑美食节，则答案 $=Ans[1][1]$ ，其中 $Ans=f \times G^T$

对于有美食节的情况:
在每个美食节做一次朴素转移，具体来说
因为每个美食节不在一个一个时间举行，先按照每个美食节的时间排序。
对于 $t[i-1]$ 到 $t[i]$ :
则 $f = f * G ^ {t[i] - t[i-1]}$
之后再特殊将 $f[1][x[i] ] = f[1][x[i]] + y[i]$。
若最后 $t[k] \ne T$ 则再将 $f = f * G ^ (T-t[k])$
但是时间复杂度为 $O(k \times (5n) ^ 3 \times \log T)$

为了优化复杂度，我们还是考虑二进制拆分优化，参见 P6569 [NOI Online #3 提高组] 魔法值
将所有 $G^1,G^2,G^4 ....$ 预处理出来，预处理时间复杂度 $O((5n) ^ 3 * \log T)$。
每一次二进制拆分 $t[i]-t[i-1]$ , 依次乘上对应的矩阵。
由于这里每一次乘都是一个 $1 \times 5n$ 的向量 $f$ 乘上一个 $5n \times 5n$ 的矩阵 $G$ ，时间复杂度只有 $O(k * (5n) ^ 2 \times logT)$

总时间复杂度 $O((5n) ^ 3 \times \log T + k \times (5n) ^ 2 \times \log T)$

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e5+5,inf=5e15;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,m,T,k;
int c[N];
struct Festival{
	int t,x,y;
}a[N];
bool edge[300][300];
void add(int u,int v){
	edge[u][v]=true;
}

struct Matrix{
	int a[300][300];
	int n,m;
	void Init(int val){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=m;j++){
				a[i][j]=val;
			}
		}
	}
}G,F,mi[32];
Matrix operator * (const Matrix &A,const Matrix &B){
	Matrix C;
	C.n=A.n,C.m=B.m;
	C.Init(-inf); 
	for(int k=1;k<=A.m;k++){
		for(int i=1;i<=C.n;i++){
			for(int j=1;j<=C.m;j++){
				C.a[i][j]=max(C.a[i][j],A.a[i][k]+B.a[k][j]);
			}
		}
	}
	return C;
}
signed main(){
	n=read(),m=read(),T=read(),k=read();
	for(int i=1;i<=n;i++){
		c[i]=read();
		for(int j=1;j<=4;j++){
			add(i+(j-1)*n,i+j*n);
		}
	}
	for(int i=1;i<=m;i++){
		int u=read(),v=read(),w=read();
		add(u+(w-1)*n,v);
	}
	for(int i=1;i<=k;i++){
		a[i].t=read(),a[i].x=read(),a[i].y=read();
	}
	
	F.n=1,F.m=5*n;
	G.n=5*n,G.m=5*n;
	F.Init(-inf);
	F.a[1][1]=c[1];
	for(int i=1;i<=5*n;i++){
		for(int j=1;j<=5*n;j++){
			if(edge[i][j]) G.a[i][j]=c[j];
			else G.a[i][j]=-inf;
		}
	}
	mi[0]=G;
	for(int i=1;i<=30;i++) mi[i]=mi[i-1]*mi[i-1]; 
	
	sort(a+1,a+k+1,[](Festival x,Festival y){return x.t<y.t;});
	a[0].t=0;
	for(int i=1;i<=k;i++){
		int t=a[i].t-a[i-1].t;
		for(int j=0;j<=30;j++)
			if(t>>j&1) F=F*mi[j];
		F.a[1][a[i].x]+=a[i].y;
	}
	if(a[k].t!=T){
		int t=T-a[k].t;
		for(int j=0;j<=30;j++)
			if(t>>j&1) F=F*mi[j];
	}
	
	if(F.a[1][1]<0) printf("-1\n");
	else printf("%lld\n",F.a[1][1]);
	return 0;
}

15.CF1051E Vasya and Big Integers

设 $f[i]$ 表示划分后 $[i,n]$ 的方案。
能从 $f[j]$ 转移到 $f[i]$ 的 $j$ 一定在 $[i+lenL,i+lenR]$ 中的一段连续区间 ( $lenR$ 为 $r$ 的长度，$lenL$ 为 $l$ 的长度)。
事实上只有 $j=i+lenR$ 和 $j=i+LenL$ 时有可能不合法，特殊判断一下(二分+ hash 或 ex_KMP) 即可。
转移时用后缀和优化。
之所以这么设计状态是因为这样基本不用考虑前导零。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e6+5,mod=998244353;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
string s,a,b;
int n,lenL,lenR;
int z[N],p1[N],p2[N];
int f[N],q[N];
void Init(){
	int l=0,r=0;
	z[1]=lenL;
	for(int i=2;i<=lenL;i++){
		if(i<=r) z[i]=min(r-i+1,z[i-l+1]);
		while(a[1+z[i]]==a[i+z[i]]) z[i]++;
		if(i+z[i]-1>r) l=i,r=i+z[i]-1;
	}
	l=0,r=0;
	for(int i=1;i<=n;i++){
		if(i<=r) p1[i]=min(r-i+1,z[i-l+1]);
		while(1+p1[i]<=lenL&&i+p1[i]<=n&&s[i+p1[i]]==a[1+p1[i]]) p1[i]++;
		if(i+p1[i]-1>r) l=i,r=i+p1[i]-1;
	}
	
	memset(z,0,sizeof z);    //清空!!!!!! 
	l=0,r=0;
	z[1]=lenR;
	for(int i=2;i<=lenR;i++){
		if(i<=r) z[i]=min(r-i+1,z[i-l+1]);
		while(b[1+z[i]]==b[i+z[i]]) z[i]++;
		if(i+z[i]-1>r) l=i,r=i+z[i]-1;
	}
	l=0,r=0;
	for(int i=1;i<=n;i++){
		if(i<=r) p2[i]=min(r-i+1,z[i-l+1]);
		while(1+p2[i]<=lenR&&i+p2[i]<=n&&s[i+p2[i]]==b[1+p2[i]]) p2[i]++;
		if(i+p2[i]-1>r) l=i,r=i+p2[i]-1;
	}
}
bool cmp1(int l,int r){
	if(r-l+1<lenL) return false;
	if(r-l+1>lenL) return true;
	if(p1[l]==lenL) return true;
	return a[1+p1[l]]<=s[l+p1[l]];
}
bool cmp2(int l,int r){
	if(r-l+1<lenR) return true;
	if(r-l+1>lenR) return false;
	if(p2[l]==lenR) return true;
	return b[1+p2[l]]>=s[l+p2[l]];	
}
bool check(int l,int r){
	if(l>r) return false;
	return cmp1(l,r)&&cmp2(l,r); 
}
signed main(){
//	freopen("cyq.in","r",stdin);
//	freopen("cyq.out","w",stdout);
	cin>>s>>a>>b;
	n=s.size(),lenL=a.size(),lenR=b.size();
	s=' '+s,a=' '+a,b=' '+b;
	Init();
	
	f[n+1]=1;
	q[n+1]=1;
	for(int i=n;i>=1;i--){
		if(s[i]=='0'){
			if(check(i,i)) f[i]=f[i+1];
		}
		else{
			int l=min(n+1,i+lenL),r=min(n+1,i+lenR);
			if(!check(i,l-1)) l++;
			if(!check(i,r-1)) r--;
			if(l<=r) f[i]=(q[l]-q[r+1]+mod)%mod;
			else f[i]=0;
		}
		q[i]=(q[i+1]+f[i])%mod;
	}
	printf("%lld\n",f[1]);
	return 0;
}

16.CF1310C Au Pont Rouge

所有子串排序后二分答案。
check 相当于要求把 $S$ 分割成 $m$ 段大小都大于一个给定子串的方案数，转移和上题类似。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e6+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int  n,m,cnt,k;
string s;
int lcp[1005][1005];
struct P{
	int l,r;
}a[N];
bool operator > (P const &x, P const &y) {
	int L=lcp[x.l][y.l];
	if (L>=x.r-x.l+1||L>=y.r-y.l+1)
		return x.r-x.l+1>y.r-y.l+1;
	return s[x.l+L]>s[y.l+L];
}
int f[1005][1005],q[1005][1005];
// f[j][i] 表示把 [i,n] 划分成 j 使每一段都比给定的大，q[j][i]表示对于 j 的后缀和。 
int check(P x){
	memset(f,0,sizeof f);
	memset(q,0,sizeof q);
	f[0][n+1]=1;
	for(int i=n+1;i>=1;i--) q[0][i]=q[0][i+1]+f[0][i];
	int l=x.l,r=x.r,len=r-l+1;
	for(int j=1;j<=m;j++){
		for(int i=n;i>=1;i--){
			int tmp=min(len,lcp[i][l]);
			if(tmp==len||s[i+tmp]>=s[l+tmp]) 
				f[j][i]=q[j-1][i+tmp+1];
		}
		for(int i=n;i>=1;i--) q[j][i]=min((long long)1e18,q[j][i+1]+f[j][i]);   //防止爆掉 
	}
	return f[m][1]; 
}
signed main(){
	n=read(),m=read(),k=read();
	cin>>s; s=' '+s;
	lcp[n][n]=1;
	for(int i=n;i>=1;i--){
		for(int j=n;j>=1;j--){
			if(i==j&&i==n) continue;
			if(s[i]==s[j]) lcp[i][j]=lcp[i+1][j+1]+1;
			else lcp[i][j]=0;
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=i;j<=n;j++){
			a[++cnt]={i,j};
		}
	}
	
	sort(a+1,a+cnt+1,greater<P>());
	
	int l=1,r=cnt,mid,ans;
	while(l<=r){
		mid=(l+r)>>1;
		if(check(a[mid])+1<=k) ans=mid,l=mid+1;
		else r=mid-1;
	}
	for(int i=a[ans].l;i<=a[ans].r;i++){
		printf("%c",s[i]);
	}
	printf("\n");
	return 0;
}

17.CF477D Dreamoon and Binary

方案数:
一个很好想的 DP , 设 $f[i][j]$ 表示最后一段为 $[j,i]$ ，划分 $[1,i]$ 的方案数。
则 $f[i][j]=\sum_{k=j-1-len+1}^{j-1} f[j-1][k]$ ，其中 $ len=i-j+1$ 。
转移用前缀和优化即可做到 $O(n^2)$。
注意当 $k=j-1-len+1$ 即 $s[k,j-1]$ 和 $s[j,i]$ 长度一样时要判断前一个是否比后一个小 , 可以预处理 LCP
对于前导$0$的处理只需要在$0$的位置不算入前缀和即可。
最小操作次数:
乍一看取模之后似乎是不能比较大小的，所以就不能 DP ,所以分析性质。
考虑最后的答案是怎么算的:
$ans = \text{打印次数+加一次数} = m+val$。
其中 $m$ 为段数, $val$ 为最后一段的值。
假设最后一段为 $s[i,n]$。
当 $i$ 前移时， $m$ 只会最多减少 $1$ ，而 $val$ 会多一个数量级，而 $m \le 5000 < 2^{17}$，
所以我们其实只需要考虑 $n-16 \le i\le n$ 的答案即可，如果这个位置的划分不合法就是第一问中 f[n][i]=0 。
我们只需要 DP 求出最小的段数即可,这里由于 $j \le i$ ，所以 DP 时记录一下后缀最小值 , 就可以也做到 $O(n^2)$
Tip:当然如果这个区间里无解还要继续往前。(见代码)

别 define int long long ，卡空间

code

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N=1e5+5,inf=0x3f3f3f3f;
const ll mod=1e9+7;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
string s;
int n; 
int lcp[5005][5005];
void Init(){
	for(int i=n;i>=1;i--){
		for(int j=n;j>=1;j--){
			if(s[i]==s[j]) lcp[i][j]=lcp[i+1][j+1]+1;
			else lcp[i][j]=0;
		}
	}
}
bool cmp(int l,int r,int x,int y){   //判断s[l,r]是否<=s[x,y] 
	int len1=r-l+1,len2=y-x+1;
	if(len1<len2) return true;
	if(len1>len2) return false;
	if(lcp[l][x]>=len1) return true;
	return s[l+lcp[l][x]]<=s[x+lcp[l][x]];
}
int f[5005][5005],q[5005][5005];
int g[5005][5005],ming[5005][5005]; //最小段数,g数组的后缀最小值 
void solve1(){
	memset(g,0x3f,sizeof g); 
	memset(ming,0x3f,sizeof ming); 
	for(int i=1;i<=n;i++){
		for(int j=1;j<=i;j++){
			if(i!=j&&s[j]=='0'){
				f[i][j]=0;
				g[i][j]=inf;
			}
			else if(j==1){
				f[i][j]=1;
				g[i][j]=1;
			} 
			else{
				int k=j-1-(i-j+1)+1; k=max(k,1);
				if(!cmp(k,j-1,j,i)) k++;
				f[i][j]=((ll)(q[j-1][j-1]+mod-q[j-1][k-1]))%mod;
				g[i][j]=ming[j-1][k]+1;
			}
			q[i][j]=((ll)(q[i][j-1]+f[i][j]))%mod;
		}
		for(int j=i;j>=1;j--) ming[i][j]=min(ming[i][j+1],g[i][j]);
	}
	printf("%d\n",q[n][n]);
}
void solve2(){
	ll mi=1,val=0,ans=inf;
	bool flag=false;  //记录是否出现了解，如果 i 在 [n-16,n] 之内没有解要继续往前 
	for(int i=n;i>=max(1,n-16);i--){
		val=val+(ll)(s[i]-'0')*mi; mi*=2ll;
		if(f[n][i]!=0) flag=true,ans=min(ans,(ll)(g[n][i]+val));
	}
	if(flag){
		printf("%lld\n",ans%mod);
		return;
	}
	
	for(int i=n-17;i>=1;i--){
		val=(val+(ll)(s[i]-'0')*mi)%mod; (mi*=2ll)%=mod;
		if(f[n][i]!=0){
			printf("%lld\n",(ll)(g[n][i]+val)%mod);
			return;
		}
	}

}
signed main(){
	cin>>s;
	n=s.size(); s=' '+s;
	Init();
	solve1();
	solve2();
	return 0;
}

18.CF1562E Rescue Niwen!

sol1(人类智慧)

先 $O(n^2)$ DP 求出所有 $LCP(i,j)$。
设 $f[l,r]$ 表示以 $[l,r]$ 这个子串为末尾的 LIS , $F[i]$ 表示 $f[i,n]$。
因为注意到对于以 $[l,r]$ 这个子串为末尾的 LIS ，我一定可以往后面接 $[l,r+1] [l,r+2], ... ,[l,n]$ ，
所以最后的答案一定是 $\max ^n_{i=1} f[i,n]$ ,即 $\max ^n_{i=1} F[i]$。

若 $LCP(i,j)=len (j<i)$ :

如果 $s[j+len]>s[i+len]$ ，则无法产生贡献
如果 $s[j+len]<s[i+len]$ 则 $F[i]=\max(F[i],F[j] + n - (i+len) +1)$ ，
就是说对于以 $[j,n]$ 这个子串为末尾的 LIS 再接上 $[i,i+len] , [i,i+len+1] , ... ,[i,n]$ 。

时间复杂度 $O(n^2)$

sol2(常规做法)

还有一种解法是根据 $LCP$ 排序 (即按字典序排序)，然后离散化，给每一个字符串赋一个代表他排名的值。
再按照题目要求排序，跑正常的 $LIS$。

时间复杂度$O(n^2 \log n^2)$,看运气可过。

code(sol1)

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int T;
int n,lcp[5005][5005],f[5005];
string s;
signed main(){
	T=read();
	while(T--){
		n=read();
		cin>>s; s=' '+s;
		for(int i=1;i<=n;i++){
			f[i]=0;
			for(int j=1;j<=n;j++){
				lcp[i][j]=0;
			}
		}
		lcp[n][n]=1;
		for(int i=n;i>=1;i--){
			for(int j=n;j>=1;j--){
				if(i==n&&j==n) continue;
				if(s[i]==s[j]) lcp[i][j]=lcp[i+1][j+1]+1;
				else lcp[i][j]=0;
			}
		}
		int ans;
		ans=n;
		for(int i=1;i<=n;i++){
			f[i]=n-i+1;
			for(int j=1;j<i;j++){
				if(s[j+lcp[i][j]] < s[i+lcp[i][j]])
					f[i]=max(f[i],f[j]+n-(i+lcp[i][j])+1);
			}
			ans=max(ans,f[i]);
		}
		printf("%d\n",ans);
	}
	return 0;
}

19.CF1701E Text Editor

若没有 home 操作，很明显不会用 right ，此时答案为 $n - LCP(S,T)$ ( LCP 为最长公共前缀)。
如果有 home , 此时策略一定是这样的:

从后往前删，每一次花费 $1$ 进行 left 或 Backspace
花 $1$ 按 home
从前往后删，每一次花费 $1$ 按 right 或花费 $2$ 先按 right 再按 Backspace
剩余中间一段 $S,T$ 是一样的不用动

考虑从前往后和从后往前两次 DP ，以从前往后为例:
$f[i][j]$ 表示从前往后操作，当前操作完光标在 $i$ 后，让 $S[1,i]$ 和 $T[1,j]$ 匹配的最小代价。
转移：

删除 $f[i][j]=min(f[i][j],f[i-1][j]+2)$
不删若 $s[i]=t[j]$ , $f[i][j]=min(f[i][j],f[i-1][j-1]+1)$

从后往前类似，用 $g[i][j]$ 表示，当前操作完光标在 $j$ 前，让 $S[i,n]$ 和 $T[j,m]$ 匹配的最小代价

但是注意到我们还会有一段，即剩余中间一段 $S,T$ 是一样的不用动，而在我们上面的转移中，这一段我们也会用移动建，但其实是不用的。
所以用 $F[i][j]$ 表示从前往后让 $S[1,i]$ 和 $T[1,j]$ 匹配的最小操作次数

删除 $F[i][j]=min(F[i][j],f[i-1][j]+2)$ ，因为要删除的话，一定是要把光标移到 $i$ 之前的，所以转移用 $f$数组
不删若$s[i]=t[j]$ , $F[i][j]=min(F[i][j],F[i-1][j-1])$ 可以不用移动。

$G[i][j]$ 的定义和转移类似

最后的答案是:

\[ \min {f[i][j] + g[i+1][j+1] + (f[i][j]!=0)} \]

最后一个是 home 操作的花费

这题卡空间，用 $short$ 存储即可 (因为不能用滚动数组)。

code

#include<bits/stdc++.h>
using namespace std;
const int N=5e3+5,inf=N;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int T,n,m;
short f[N][N],g[N][N],F[N][N],G[N][N];
char s[N],t[N];
int Min(int x,int y){  //之所以手写是因为min不能比较 short 和 int 
	if(x>y) return y;
	return x;
}
signed main(){
	T=read();
	while(T--){
		n=read(),m=read();
		scanf("%s%s",s+1,t+1);
		for(int i=0;i<=n+1;i++){
			for(int j=0;j<=m+1;j++){
				F[i][j]=G[i][j]=f[i][j]=g[i][j]=inf;
			}
		}
		
		F[0][0]=f[0][0]=0;
		for(int i=1;i<=n;i++){
			for(int j=0;j<=m;j++){    //注意把 j=0 循环上 
				F[i][j]=f[i][j]=f[i-1][j]+2;
				if(s[i]==t[j])	f[i][j]=Min(f[i][j],f[i-1][j-1]+1),F[i][j]=Min(F[i][j],F[i-1][j-1]);
			}
		}
		
		G[n+1][m+1]=g[n+1][m+1]=0;
		for(int i=n;i>=1;i--){
			for(int j=m+1;j>=1;j--){   //注意把 j=m+1 循环上 
				G[i][j]=g[i][j]=g[i+1][j]+1;
				if(s[i]==t[j]) g[i][j]=Min(g[i][j],g[i+1][j+1]+1),G[i][j]=Min(G[i][j],G[i+1][j+1]);
			}
		}
		
		int ans=inf;
		for(int i=0;i<=n;i++){
			for(int j=0;j<=m;j++){
				ans=min(ans,F[i][j]+G[i+1][j+1]+(F[i][j]!=0));
			}
		}
		
		if(ans==inf) printf("-1\n");
		else printf("%d\n",ans);
	}
	return 0;
}

20.CF1954D Colored Balls

经典结论:一个集合的答案为 $max(\lceil \frac {sum}{2} \rceil,maxn)$
$sum$ 为集合元素总个数，$maxn$ 为出现次数最多的数的个数，除法取上整

背包求方案数再乘上答案即可。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=5e3+5,mod=998244353;
inline int read(){
	int w=1,s=0;
	char c=getchar();
	for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
	for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
	return w*s;
}
int n;
int a[N],f[N],g[N];
int calc(int x){
	if(x&1) return x/2+1;
	return x/2;
}
signed main()
{
	n=read();
	for(int i=1;i<=n;i++) a[i]=read();
	sort(a+1,a+n+1);
	int sum=0,ans=0;
	f[0]=1;
	for(int i=1;i<=n;i++){
		sum+=a[i];
		for(int j=N-1;j>=a[i];j--){
			g[j]=f[j-a[i]];
			(f[j]+=f[j-a[i]])%=mod;
		}
		for(int j=a[i];j<=sum;j++)
			(ans+=g[j]*max(calc(j),a[i]))%=mod;
	}
	printf("%lld\n",ans);
	return 0;
}

21.染色

题目大意:给你一个序列，每个位置有一个颜色，求把这个序列分成若干段，每段颜色数的平方之和的最小值。

暴力DP $O(n^2)$: $f[i]$ 表示把前 $i$ 个位置染成对应颜色的最小值，转移时枚举 $j$ , $f[i]=min(f[i],f[j]+calc(j,i)^2)$ calc表示颜色数量

经典套路之---考虑DP值的范围:
注意到最终答案一定不大于n,因为我完全可以每一次只染色长度为 $1$ 的区间
所以颜色数我们只用枚举到 $\sqrt n$ 即可

具体来讲: 因为我们确定了颜色数之后，肯定一次染的长度越多越好，而颜色数我们只需要知道每个颜色的最后一个位置即可,所以我们只需要维护最后 $\sqrt n$ 个颜色的最后一个位置，$O(n \times \sqrt n)$转移

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e4+5,inf=5e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,a[N],f[N];
unordered_map<int,int> pos;
set<int> s;
signed main(){
//	freopen("cyq.in","r",stdin);
//	freopen("cyq.out","w",stdout);
	while(scanf("%lld",&n)!=EOF){
		for(int i=1;i<=n;i++) a[i]=read(),f[i]=inf;
		int t=sqrt(n)+1+1;
		f[0]=0;  //注意不能写f[1]=1 
		s.clear();
		s.insert(0);
		for(int i=1;i<=n;i++){
			if(!pos[a[i]]||(s.find(pos[a[i]])==s.end())){
				pos[a[i]]=i,s.insert(i);
				if(s.size()>t) s.erase(s.begin());
			}
			else{
				s.erase(pos[a[i]]);
				pos[a[i]]=i;
				s.insert(pos[a[i]]);
			}
			int cnt=s.size()-1;
			for(int x:s){
				if(cnt==0) break;
				f[i]=min(f[i],f[x]+cnt*cnt);   //染色染[x+1,i] 
				cnt--;
			}
		}
		printf("%lld\n",f[n]);
		for(int i=1;i<=n;i++) pos.erase(a[i]);
	}
	return 0;
}

22.二进制翻转

对于操作序列:
$(x_1,y_1),(x_2,y_2),...,(x_k,y_k)$
如果 $x_i=x_j$ , 那我们可以把他们消掉，对于 y 也同理
假设消掉后剩下 $a$ 个互不相同 $x$，和 $b$ 个互不相同的 $y$,那么容易得到还剩 $a\times m+b\times n-2\times a \times b$ 个 $1$，我们完全可以暴力枚举这个 $a$ 和 $b$,我们只需要分开计算方案数即可。

设 $f[i][j]$ 表示构造长度为 $i$ 的序列 ${x_1,x_2,...,x_i}$,按如上方法消掉之后剩余 $j$ 个的方案数，转移时:

第 $i$ 个 $x$ 和前面的某个 $x$ 抵消了，所以 $f[i-1][j+1] \times (j+1) \to f[i][j]$
第 $i$ 个 $x$ 和前面的任何一个 $x$ 都不一样，所以 $f[i-1][j-1] \times (n-j+1) \to f[i][j]$

$g[i][j]$同理

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=3005,mod=1e9+7;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,m,k,s; 
int f[N][N],g[N][N];
signed main(){
	n=read(),m=read(),k=read(),s=read();
	
	f[0][0]=1;
	for(int i=1;i<=k;i++){
		for(int j=0;j<=n;j++){
			f[i][j]=f[i-1][j+1]*(j+1)%mod;
			if(j>0) (f[i][j]+=f[i-1][j-1]*(n-j+1)%mod)%=mod;
		}
	}
	
	g[0][0]=1;
	for(int i=1;i<=k;i++){
		for(int j=0;j<=m;j++){
			g[i][j]=g[i-1][j+1]*(j+1)%mod;
			if(j>0) (g[i][j]+=g[i-1][j-1]*(m-j+1)%mod)%=mod;
		}
	}
	
	int ans=0;
	for(int a=0;a<=n;a++){
		for(int b=0;b<=m;b++){
			if(a*m+b*n-2ll*a*b!=s) continue;
			if(a>k||b>k||((k-a)%2ll!=0)||((k-b)%2ll!=0)) continue;
			(ans+=f[k][a]*g[k][b]%mod)%=mod;
		}
	}
	printf("%lld\n",ans);
	return 0;
}

23.不稳定的传送门

设 $f[i]$ 表示 $i$ 到 $n$ 的最小期望花费,令 $f[n]=n$。

假设 $i$ 的所有出边为 $(t_j,p_j,w_j) (1 \le j \le cnt_i)$,$cnt_i$ 是 $i$ 的出边数量。
我们按照一定顺序安排尝试顺序后则

\[期望 =w_1 + p_1 \times f[t_1] + (1-p_1) \times (w_2 + p_2 \times f[t_2] +(1 - p_2) \times (...) ) \]

我们适当换一下元，令 $c_j=w_j+p_j \times f[t_j]$ (不是题目描述的 $c$),则:

\[\begin{aligned} 期望 &=c_1+(1-p_1) \times (c_2+(1-p_2) \times (c_3+(1-p_3) \times (...) ) ) \\ &=c_1 + (1-p_1)\times c_2 + (1-p_1)\times (1-p_2) \times c_3 + ... \\ &= \sum_{j=1}^{cnt_i} (\prod_{k=1}^{j-1} 1-p_k) \times cj \\ \end{aligned} \]

要使它尽可能小，我们考虑邻项交换:
对于相邻两项 j,j+1,
原来的期望花费 $= (1-p_1) \times (1-p_2)\times ...\times (1-p_{j-1})\times c_j + (1-p_1)\times (1-p_2)\times ...\times (1-p_{j-1})\times (1-p_j)\times c_{j+1}$
交换之后的花费 = $= (1-p_1) \times (1-p_2)\times ...\times (1-p_{j-1})\times c_{j+1} + (1-p_1)\times (1-p_2)\times ...\times (1-p_{j-1})\times (1-p_{j+1})\times c_j$
当前一项比后一项小时，消去相同的项得到:
$c_j+(1-p_j)\times c_{j+1} < c_{j+1}+(1-p_{j+1})\times c_j$
按照这个写 cmp 即可

code

include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,m;
struct P{
	int t;
	double p;
	int w;
	double c;
};
vector<P> G[N];
double f[N];
bool cmp(P x,P y){
	return 1.0*x.c+(1.0-x.p)*y.c < 1.0*y.c+(1.0-y.p)*x.c;
}
signed main(){
	n=read(),m=read();
	for(int i=1;i<n;i++){
		int w=read();
		G[i].push_back({i+1,1.0,w,0});
	}
	for(int i=1;i<=m;i++){
		int s=read(),t=read();
		double p;
		cin>>p;
		int w=read();
		G[s].push_back({t,p,w,0});
	}
	f[n]=0;
	for(int u=n-1;u>=1;u--){
		for(int i=0;i<G[u].size();i++)
			G[u][i].c=G[u][i].w*1.0+G[u][i].p*f[G[u][i].t];
		sort(G[u].begin(),G[u].end(),cmp);
		double g=1;
		for(P e:G[u]){
			f[u]+=e.c*g;
			g*=(1.0-e.p);
		}	
	}
	
	printf("%.2lf",f[1]);
	return 0;

24.CF1444D Rectangular Polyline

这题其实没有什么动态规划，主要是构造，
考虑到这个是动态规划题单，并且题解有点复杂，所以具体见Booksnow 的题解
~~首先排除我懒~~。

只需要注意下涉及到的 bitset优化01背包

code

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int T;
int n,m,l[N],p[N],sumx,sumy; 
vector<int> x[2],y[2];
int dx[N],dy[N],cnt;
bitset<N*N> f[N];
signed main(){
	T=read();
	f[0][0]=1;    //不需要重复赋值 
	while(T--){
		sumx=sumy=0;
		x[0].clear(),x[1].clear();
		y[0].clear(),y[1].clear();
		
		n=read();
		for(int i=1;i<=n;i++) l[i]=read(),sumx+=l[i];
		m=read();
		for(int i=1;i<=m;i++) p[i]=read(),sumy+=p[i];
		if(n!=m||(sumx&1)||(sumy&1)){
			puts("No");
			continue;
		}
		
		for(int i=1;i<=n;i++) f[i]=f[i-1]|(f[i-1]<<l[i]);
		if(!f[n][sumx/2]){
			puts("No");
			continue;
		}
		int lst=sumx/2;
		for(int i=n;i>=1;i--)
			if(lst>=l[i]&&f[i-1][lst-l[i]]) lst-=l[i],x[0].push_back(l[i]);
			else x[1].push_back(l[i]);
			
		for(int i=1;i<=m;i++) f[i]=f[i-1]|(f[i-1]<<p[i]);
		if(!f[m][sumy/2]){
			puts("No");
			continue;
		}
		lst=sumy/2;
		for(int i=m;i>=1;i--)
			if(lst>=p[i]&&f[i-1][lst-p[i]]) lst-=p[i],y[0].push_back(p[i]);
			else y[1].push_back(p[i]);
			
		if(x[0].size()>y[0].size()) swap(x[0],x[1]);
		if(x[0].size()>y[0].size()) swap(y[0],y[1]);
		
		puts("Yes");
		cnt=0;
		for(int v:x[0]) dx[++cnt]=v;
		for(int v:x[1]) dx[++cnt]=v;
		cnt=0;
		for(int v:y[0]) dy[++cnt]=v;
		for(int v:y[1]) dy[++cnt]=v;
	
		sort(dx+1,dx+x[0].size()+1,greater<int>());
		sort(dx+x[0].size()+1,dx+y[0].size()+1,greater<int>());
		sort(dx+y[0].size()+1,dx+n+1,greater<int>());
		
		sort(dy+1,dy+x[0].size()+1);
		sort(dy+x[0].size()+1,dy+y[0].size()+1);
		sort(dy+y[0].size()+1,dy+m+1);
		int X=0,Y=0;
		for(int i=1;i<=x[0].size();i++){
			X+=dx[i];printf("%d %d\n",X,Y);
			Y+=dy[i];printf("%d %d\n",X,Y);
		}
		for(int i=x[0].size()+1;i<=y[0].size();i++){
			X-=dx[i];printf("%d %d\n",X,Y);
			Y+=dy[i];printf("%d %d\n",X,Y);
		}
		for(int i=y[0].size()+1;i<=n;i++){
			X-=dx[i];printf("%d %d\n",X,Y);
			Y-=dy[i];printf("%d %d\n",X,Y);
		}		
	}
	return 0;
}

25.CF1178F1 Short Colorful Strip

这是 F题的弱化版，保证了最终序列是个排列。

很明显两次染色操作要么包含要么相离，绝对不可能相交。

考虑区间DP: $f[i][j]$ 表示染完区间 $[i,j]$ 的方案数
显然我们先染的一定是最小的那个颜色，假设那个颜色的位置为 $k$。
枚举第一次染色区间 $[x,y]$，显然 $[x,y]$ 包含 $k$ ，
即 $l \le x \le k \le y \le r$。
因为后面就不能再染 $k$ 这个位置了，且染色操作绝对不可能相交，所以区间: $[l,x-1],[x,k-1],[k+1,y],[y+1,r]$ 是独立的，把他们的方案数乘起来即可。
注意这里每个区间的先后顺序是唯一的(按照最小颜色排)，所以不用乘 $4!$
即:

\[ f[l,r]=\sum_{x=l}^{k}\sum_{y=k}^{r}(f[l,x-1] \times f[x,k-1]) \times (f[k+1,y] \times f[y+1,r]) \]

注意到这样是 $O(n^4)$ ,所以把 $x,y$ 拆开枚举即可:

\[ f[l,r]=(\sum_{x=l}^{k}f[l,x-1] \times f[x,k-1]) \times (\sum_{y=k}^{r}f[k+1,y] \times f[y+1,r]) \]

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5,mod=998244353;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,m,a[505],f[505][505];
signed main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	n=read(),m=read();
	for(int i=1;i<=m;i++) a[i]=read();
	for(int l=0;l<=m+1;l++){
		for(int r=0;r<=m+1;r++){
			f[l][r]=1;
		}
	}
	for(int len=1;len<=m;len++){
		for(int l=1;l+len-1<=m;l++){
			int r=l+len-1;
			if(len>1){
				int sum1=0,sum2=0,ming=INT_MAX,pos;
				for(int i=l;i<=r;i++)
					if(a[i]<ming) ming=a[i],pos=i;
				for(int x=l;x<=pos;x++) (sum1+=f[l][x-1]*f[x][pos-1])%=mod;
				for(int y=pos;y<=r;y++) (sum2+=f[pos+1][y]*f[y+1][r])%=mod;
				f[l][r]=sum1*sum2%mod;
			}
		}
	}
	printf("%lld\n",f[1][m]);
	return 0;
}

26.CF1178F2 Long Colorful Strip

这题和上一题唯一的区别就是 : 这题纸带很长，每一种颜色不一定只有一种。
为了套用上一题的区间DP做法，考虑怎么缩小 $m$。
注意到，从一开始的一个颜色段，每一次操作最多增加 $2$ 个颜色段，即，如果最终状态颜色段的数目$>2\times n+1$,那肯定无解。
并且对于一个最终状态的颜色段，他们肯定是一起被染色的，否则后面就无法把他们一起染成目标颜色，于是可以把所有颜色段看成一个点，这样最多有 $2 \times n+1$ 个点，由于 $O(n^3)$ 肯定跑不满，所以可以借鉴上一题的做法。

因为每一种颜色不一定只有一种,即每一个区间 $[l,r]$ 不一定只有一个最小的颜色,所以我们枚举的 $[x,y]$ 要包含所有的 $k_1,k_2,k_3,k_4,...k_{cnt}$。

转移的式子为:

\[\begin{aligned} f[l,r] &=\sum_{x=l}^{k_1}\sum_{y=k_{cnt}}^{r}f[l,x-1] \times f[x,k_1-1] \times f[k_1+1,k_2-1] \times ... \times f[k_{cnt-1}+1,k_{cnt}-1] \times f[k_{cnt}+1,y] \times f[y+1,r]\\ &=(\sum_{x=l}^{k_1}f[l,x-1] \times f[x,k1-1]) \times (\sum_{y=k_{cnt}}^{r}f[kcnt+1,y] \times f[y+1,r]) \times (f[k1+1,k2-1] \times ... \times f[k[cnt-1]+1,kcnt-1]) \end{aligned} \]

实现时还有一个细节要注意的是，比如样例中的: 2 1 2
虽然这一看就是 $0$ ,但是程序会输出 $4$。
这是因为当我们根据 $1$ 把它分成 $2$ 和 $2$ 两半后，这两半并不是独立的，要把它们染成 $2$，必然要经过 $1$。
特判也很好处理:如果 $[l,r]$ 这段区间里的颜色中有颜色并没有全部出现则把它的DP值设为 $0$

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+5,mod=998244353;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,m;
int a[N],b[N],f[1005][1005],pre[1005][505];
signed main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	n=read(),m=read();
	for(int i=1;i<=m;i++){
		b[i]=read();
	}
	int cnt=0;
	for(int i=1;i<=m;i++){
		int j;
		for(j=i;b[j]==b[i];j++) ;
		a[++cnt]=b[i],i=j-1;
	}
	m=cnt;
	if(m>2*n+1){
		printf("%d\n",0);
		return 0;	
	} 
	for(int i=1;i<=m;i++){
		pre[i][a[i]]=1;
	}
	for(int i=1;i<=m;i++){
		for(int j=1;j<=n;j++){
			pre[i][j]+=pre[i-1][j];
		}
	}
	for(int l=0;l<=m+1;l++){
		for(int r=0;r<=m+1;r++){
			f[l][r]=1;
		}
	}
	for(int len=1;len<=m;len++){
		for(int l=1;l+len-1<=m;l++){
			int r=l+len-1;
			for(int i=l;i<=r;i++){
				int cnt1=pre[r][a[i]]-pre[l-1][a[i]],cnt2=pre[m][a[i]];
				if(cnt1<cnt2){
					f[l][r]=0;
					break;
				}
			}
			if(len>1){
				int sum1=0,sum2=0,tmp=1,ming=INT_MAX;
				for(int i=l;i<=r;i++)
					if(a[i]<ming) ming=a[i];
				int st=-1,ed=-1,lst=-1;
				for(int i=l;i<=r;i++){
					if(a[i]==ming){
						if(lst!=-1)
							(tmp*=f[lst+1][i-1])%=mod;
						if(st==-1) st=i;
						lst=ed=i;
					}
				}
				for(int x=l;x<=st;x++) (sum1+=f[l][x-1]*f[x][st-1])%=mod;
				for(int y=ed;y<=r;y++) (sum2+=f[ed+1][y]*f[y+1][r])%=mod;
				f[l][r]*=sum1*sum2%mod*tmp%mod;
			}
		}
	}
	printf("%lld\n",f[1][m]);
	return 0;
}

27.[CEOI2016] kangaroo

题目要求相当于是说只能来回横跳。

相当于要构造一个排列，这个排列满足：
对于每个连续的三个数，中间那个数是最大的或最小的，即整个序列呈波浪型。

关于这种序列满足一定形状的题，套路就是考虑从小到大插入每个位置。
设 $f[i][j]$ 表示插入到 $i$ , 一共有 $j$ 个连续段的情况,接下来对于 $i+1$ ，如果 $i+1 \ne s或t$，有三种情况:

自成一段，即插在空隙里，一共有 $j+1$ 个空隙，但如果此时已经插入了 $s$或$t$ ，头或尾不能插
把两段接在一起，此时 $i+1$ 一定大于其左右两个数(因为是从小到大)，即他是波峰，一定满足题意，一共有 $j-1$ 个选择
加在一段的开头或结尾，假设接在开头，那么此时 i+1 的右边比它要小，但左边由于还没放，到时候肯定比它要大，这样就会出现单调递减的三个数，就不符合题意了，所以不会出现这种情况。(当然如果 $i+1=s或t$时是可以的)

代码里用的是填表法，在 $i=s或t$ 时要特判,此时只能放在开头/结尾。

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e3+5,mod=1e9+7;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,s,t,f[N][N]; 
signed main(){
	n=read(),s=read(),t=read();
	f[0][0]=1;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=i;j++){
			if(i==s||i==t) f[i][j]=(f[i-1][j-1]+f[i-1][j])%mod;
			else f[i][j]=((j-(i>s)-(i>t))*f[i-1][j-1]%mod+j*f[i-1][j+1]%mod)%mod;
		}
	}
	printf("%lld\n",f[n][1]);
	return 0;
}

28.CF1312D Count the Arrays

套路和上题类似。

先假设我们是用给定的 $n-1$ 个数来构造这个序列。
我们考虑从大到小考虑这 $n-1$ 个数。

设 $f[i][0/1]$ 表示构造长度为 $i$ 的满足条件的序列，并且没有/有出现两个相同的数，那对于

$f[i][0]$ ：我可以把当前考虑的这个数放在序列的开始，也可以放在结尾 $f[i][0]\gets 2 \times f[i-1][0]$
$f[i][1]$ ：这个数如果不是相同的那个数则 $f[i][1]\gets2* \times[i-1][1]$，否则我就开头放一个，结尾放一个 $f[i][1] \gets f[i-2][0]$

我们只需要随便从 $m$ 个数里选出 $n-1$ 个数就好了，答案为 $f[n][1] \times C_m^{n-1})$

几个细节:

$i=1$时，放在开头和结尾是一样的，不用$\times2$
只有 $i \ge 3$时才能进行 $f[i][1] \gets f[i-2][0]$ 的转移，不然不满足严格单调

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5,mod=998244353;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,m,f[N][2];
int inv[N],fact[N],q[N];
int C(int n,int m){
	if(n<m) return 0;
	return fact[n]*q[m]%mod*q[n-m]%mod; 
}
signed main(){
	n=read(),m=read();
	fact[0]=1;
	for(int i=1;i<N;i++) fact[i]=fact[i-1]*i%mod;
	inv[1]=1;
	for(int i=2;i<N;i++) inv[i]=(mod-mod/i)*inv[mod%i]%mod;
	q[0]=1;
	for(int i=1;i<N;i++) q[i]=q[i-1]*inv[i]%mod;

	f[0][0]=1;
	for(int i=1;i<=n;i++){
		if(i==1){
			(f[i][0]=f[i-1][0])%=mod;
			(f[i][1]=f[i-1][1])%=mod;
		}
		else{
			(f[i][0]=2*f[i-1][0])%=mod;
			(f[i][1]=2*f[i-1][1])%=mod;
		}
		if(i>=3) (f[i][1]+=f[i-2][0])%=mod;
	}
	printf("%lld\n",f[n][1]*C(m,n-1)%mod);
	return 0;
}

29.CF1312E Array Shrinking

考虑区间DP,一段区间 $[l,r]$ 要么直接合成一个数，否则一定可以找到一个分界点 $i$,使 $f[l][r]=f[l][i]+f[i+1][r]$,分别进行DP即可。

code

#include<bits/stdc++.h>
using namespace std;
const int N=500+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,a[N];
int f[N][N];  //f[l][r]表示[l,r]剩余的最小长度 
int g[N][N];  //g[l][r]表示区间[l,r]缩成一个数时的值，如果不能就=0 
signed main(){
	n=read();
	for(int i=1;i<=n;i++) a[i]=read();
	for(int len=1;len<=n;len++){   
		for(int l=1;l+len-1<=n;l++){
			int r=l+len-1;
			if(len==1) g[l][r]=a[l];
			else if(len==2){
				if(a[l]==a[r]) g[l][r]=a[l]+1; 
			}
			else{
				for(int i=l;i<=r;i++){
					if(g[l][i]==g[i+1][r]&&g[l][i]!=0){
						g[l][r]=g[l][i]+1;
						break;
					}
				}				
			}
		}
	}
	for(int len=1;len<=n;len++){
		for(int l=1;l+len-1<=n;l++){
			int r=l+len-1;
			f[l][r]=r-l+1;
			if(g[l][r]) f[l][r]=1;
			else{
				for(int i=l;i<=r;i++){
					f[l][r]=min(f[l][r],f[l][i]+f[i+1][r]);
				}
			}
		}
	}
	printf("%d\n",f[1][n]);
	return 0;
}

30.CF1312G Autocompletion

首先按照题目的意思可以建出一个Trie(这个建的方式有点奇怪，可以看代码)

假设 $f[i]$ 表示打印出 $i$ 号节点对应的字符串所需要的最小花费，$id[i]$ 表示 $i$ 号节点对应的字符串在 $S$ 中的字典序。

做一个树形DP: $f[i]=min(f[fa]+1,f[j]+id[i]-id[j])$，其中 $j$ 是 $i$ 的祖先，即 $j$ 表示的字符串是 $i$ 的前缀。
考虑优化后面的转移，用一个栈来存储 $f[i]-id[i]$，
在遍历到 $i$ 的时候如果栈顶值比我大，那就入栈，回溯如果栈里面有就出栈，这样转移时直接取出栈顶即可，并且保证了栈里面的一定都是 i 的祖先

$id$ 数组也不用真的建出来，只需要用变量维护即可，只不过那些不是 S 中的节点是不能算在里面的。

code

#include<bits/stdc++.h>
#define PII pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=1e6+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,m,id,a[N];
int ch[N][30],f[N];
bool stater[N];
stack<PII> st;
void dfs(int u){ //遍历到 u 的时候 f[u] 已经算出来了
	if(!st.size()||(st.top().se>f[u]-id)) st.push({u,f[u]-id});
	id+=stater[u];   //这里 id 其实表示的是比它字典序小的在 S 中的个数 
	for(int i=0;i<=25;i++){
		if(!ch[u][i]) continue;
		int v=ch[u][i];
		f[v]=f[u]+1;
		if(st.size()&&stater[v]) f[v]=min(f[v],st.top().se+id+1);  
		/*
			首先自动补全的结果要是S中的字符串，所以要满足 stater[v]=true
			其次，id[v]-id[u]在这里表示的是从u开始到v(包括u,不包括v)中字典序比 v 小的个数，但实际上是要算上 v 的，所以要 +1 
		*/ 
		dfs(v); 
	}
	if(st.size()&&st.top().fi==u) st.pop();
}
signed main(){
	n=read();
	for(int i=1;i<=n;i++){
		int x=read();
		char c;
		cin>>c;
		ch[x][c-'a']=i;
	}
	int m=read();
	for(int i=1;i<=m;i++){
		a[i]=read();
		stater[a[i]]=true;
	}
	
	dfs(0);
	
	for(int i=1;i<=m;i++) printf("%d ",f[a[i]]);
	puts("");
	return 0;
}

31.CF1580D Subsequence

不会笛卡尔树，但是看到题解区的妙妙解法......

题目的式子非常大便，我们考虑把它翻译成人话:
一个子序列的价值为: $sum*m - 每两个数及他们之间的所有数的\min$。

设 $f[l][r][k]$ 表示在 $[l,r]$ 中选出 $k$ 个数的最大代价(为了方便我们前面那一项不 $\times k$,而是还是$\times m$)。
假设 $[l,r]$ 的最小值位置是 $pos$,如果最后选出的数不跨越 $pos$,可以递归分治。
现在考虑跨越 $pos$ 的情况,我们有两个转移:

$f[l][pos-1][i]+f[pos+1][r][j] - 2 \times i \times j \times a[pos] \to f[l][r][i+j]$
$f[l][pos-1][i]+f[pos+1][r][j] + m\times a[pos] - [2\times (i+1) \times (j+1)-1] \times a[pos] \to f[l][r][i+j+1]$

我们来解释一下:

不选择 $a[pos]$,那么左端点在 $a[pos]$ 左边，右端点在 $a[pos]$ 右边的贡献就是 $-2\times i\times j\times a[pos]$ ($\times 2$是因为每一对会贡献两次，因为题目中的 $j$ 是从 $1$ 开始，而不是 $i$)
选择 $a[pos]$,那么左端点 $pos$ 或在 $a[pos]$ 左边，右端点 $=pos$ 或在 $a[pos]$ 右边的贡献是 $-[2\times (i+1)\times (j+1)-1]\times a[pos]$ ，$-1$ 是因为当计算题目中的 $f$ 时左右端点都在 $pos$ 时只能贡献一次

递归分治求解,时间复杂度可以近似认为是:
$T(n)=2 \times T(\frac{n}{2})+O(n^2)$
根据主定理他等于 $O(n^2)$

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,m,a[N]; 
vector<int> work(int l,int r){
	vector<int> f(r-l+2,LLONG_MIN);
	f[0]=0;
	if(l>r) return f;
	int pos=l;
	for(int i=l+1;i<=r;i++) if(a[pos]>a[i]) pos=i;
	vector<int> fl=work(l,pos-1),fr=work(pos+1,r);
	for(int i=0;i<fl.size();i++){
		for(int j=0;j<fr.size();j++){
			f[i+j]=max(f[i+j],fl[i]+fr[j]-2*i*j*a[pos]);
			f[i+j+1]=max(f[i+j+1],fl[i]+fr[j]+m*a[pos]-(2*(i+1)*(j+1)-1)*a[pos]);
		}
	} 
	return f;
}
signed main(){
	n=read(),m=read();
	for(int i=1;i<=n;i++) a[i]=read();
	printf("%lld\n",work(1,n)[m]);
	return 0;
}

32.P1220 关路灯

经典套路之——费用提前计算。

如果设 $f[l][r][0/1]$ 表示关掉区间 $[l,r]$ 内的路灯后,且最后停在 $l/r$,区间 $[l,r]$ 的路灯的最小花费。
不难想到是从 $f[l+1][r]$ 和 $f[l][r-1]$ 转移过来。
但是转移时我们无法知道从开始到现在经过的时间，也就无法知道新加进来的路灯到底消耗了多少。

设 $f[l][r][0/1]$ 表示关掉区间 $[l,r]$ 内的路灯后,且最后停在 $l/r$,所有路灯的最小花费。
以从 $f[l+1][r][0]$ 转移到 $f[l][r][0]$ 为例，在转移时，我们不用再考虑在关 $[l+1,r]$ 内的路灯时的其他路灯的消耗。
只需要加上从 $l+1$ 走到 $l$ 这段时间里，$[1,l]$ 和 $[r+1,n]$ 路灯的功率消耗。
前缀和优化一下即可，转移显然。

code

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,c,a[55],w[55],f[55][55][2];
int pre[55];
int calc(int l,int r){
	return pre[r]-pre[l-1];
}
signed main(){
	n=read(),c=read();
	for(int i=1;i<=n;i++){
		a[i]=read(),w[i]=read();
		pre[i]=pre[i-1]+w[i];
	}
	memset(f,0x3f,sizeof f);
	for(int len=1;len<=n;len++){
		for(int l=1;l+len-1<=n;l++){
			int r=l+len-1;
			if(c<l||c>r) continue;
			if(len==1) f[l][r][0]=f[l][r][1]=0;
			else{
				f[l][r][0]=min( f[l+1][r][0] + (a[l+1]-a[l])*(pre[n]-calc(l+1,r)) , f[l+1][r][1] + (a[r]-a[l])*(pre[n]-calc(l+1,r)) );
				f[l][r][1]=min( f[l][r-1][1] + (a[r]-a[r-1])*(pre[n]-calc(l,r-1)) , f[l][r-1][0] + (a[r]-a[l])*(pre[n]-calc(l,r-1)) );
			}
		}
	}
	printf("%d\n",min(f[1][n][0],f[1][n][1]));
	return 0;
}

33.抢鲜草

和上题几乎一模一样。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e3+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,x,a[N];
int f[N][N][2];
/*
	考虑贡献提前计算 
	f[l][r][0/1]: 表示kona采集完所有的 [l,r] 中的草，最后在 i/j 时，所有草的最小损失青草量
	(注意"所有") 
*/
signed main(){
	n=read(),x=read();
	for(int i=1;i<=n;i++) a[i]=read();
	sort(a+1,a+n+1);
	
	memset(f,0x3f,sizeof f); 
	for(int len=1;len<=n;len++){
		for(int l=1;l+len-1<=n;l++){
			int r=l+len-1;
			if(l==r){
				f[l][r][0]=f[l][r][1]=abs(a[l]-x)*n;	
			}
			else{
//				f[l][r][0]=min(f[l+1][r][0] + (a[l+1]-a[l]) * (n-(r-(l+1)+1)),f[l+1][r][1] + (a[r]-a[l]) * (n-(r-(l+1)+1)) );   //最原始的式子方便理解 
				f[l][r][0]=min(f[l+1][r][0] + (a[l+1]-a[l]) * (n-r+l),f[l+1][r][1] + (a[r]-a[l]) * (n-r+l));
				f[l][r][1]=min(f[l][r-1][1] + (a[r]-a[r-1]) * (n-r+l),f[l][r-1][0] + (a[r]-a[l]) * (n-r+l));
			}
		}
	}
	printf("%lld\n",min(f[1][n][0],f[1][n][1]));
	return 0;
}

34.P4161 [SCOI2009] 游戏

如果把它根据对应关系连边会得到若干环，假设第 $i$ 个环的环长为 $len[i]$。那么这个环里的数要恢复原样就要 $len[i]$ 步。进一步的，容易得出整个序列要恢复原样需要 $lcm(len[1],len[2],...)$。
问题转化为:给你一个 $n$ , 构造若干个数，使得他们的和为 $n$, 求他们的 $lcm$ 的可能的情况数。

怎么构造出尽可能多的 $lcm$?
如果每一次这若干个数都互质，那他们的 $lcm = 他们的乘积$，从而每一次都不一样。
具体的，我们只需要让每个数都形如 $pi^{ki}$ ($pi$是质数，$ki$是非负整数) ，那根据算数基本定理，只要方案不同，他们的乘积($lcm$)就不同。

小小的证明：如果有一个构造方案，里面的数不互质，我们完全可以把它们转换成形如上述的数列(每个质因子只保留对应的一个数),并且 $lcm$ 不变，而且他们的总和会变小，我们只需要再往里面塞 $1$ ,就可以了。
即任意一个情况都可以转化成上述构造方法。

设 $f[i][j]$ 表示用前 $i$ 个质数，凑出和为 $j$ 的方案数,$f[i][j]=f[i-1][j-pi^k]$，因为可以往里面塞好多个 $1$ ，所以我们钦定 $k>0$；因为 $i$ 可以不选，所以 $f[i][j]+=f[i-1][j]$。
初始化 $f[0][0]=1$。
最后的答案是 $\sum_{j=0}^{n} f[max_i][j]$ ($max_i$是最大的不超过 $n$ 的质数) 。

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e3+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n;
bool stater[N];
int cnt,pri[N];
void Eular(int n){
	stater[1]=1;
	for(int i=2;i<=n;i++){
		if(!stater[i]) pri[++cnt]=i;
		for(int j=1;j<=cnt&&i*pri[j]<=n;j++){
			stater[i*pri[j]]=true;
			if(i%pri[j]==0) break;
		}
	}
}
int f[N][N];
signed main(){
	n=read();
	Eular(n); 
	
	f[0][0]=1;
	for(int i=1;i<=cnt;i++){
		for(int j=0;j<=n;j++){
			f[i][j]=f[i-1][j];
			for(int k=pri[i];k<=j;k*=pri[i]) f[i][j]+=f[i-1][j-k];
		}
	}
	int ans=0;
	for(int j=0;j<=n;j++) ans+=f[cnt][j];
	printf("%lld\n",ans);
	return 0;
}

35.P6280 [USACO20OPEN] Exercise G

这题和上一题基本上是一样的。

一样的图论连边得出每个排列需要的步数为$lcm(len[i])$。
一样的分析过程:我们只需要让每个数都形如 $pi^{ki}$ ($pi$是质数，$ki$是非负整数)。
基本一样的DP状态：
$f[i][j]$ 表示用前 $i$ 个质数，凑出和为 $j$ 的所有 $lcm$ 的和。
基本一样的转移:$f[i][j]=f[i-1][j-i^k]*(i^k)$ (因为互素，所以直接乘以 $i^k$ 就是新的 $lcm$)。
唯一不一样的:$N=1e4$,所以滚动数组。

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e4+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,mod;
bool stater[N];
int cnt,pri[N];
void Eular(int n){
	stater[1]=1;
	for(int i=2;i<=n;i++){
		if(!stater[i]) pri[++cnt]=i;
		for(int j=1;j<=cnt&&i*pri[j]<=n;j++){
			stater[i*pri[j]]=true;
			if(i%pri[j]==0) break;
		}
	}
}
int f[N];
signed main(){
	n=read(),mod=read();
	Eular(n); 
	
	f[0]=1;
	for(int i=1;i<=cnt;i++){
		for(int j=n;j>=0;j--){
			for(int k=pri[i];k<=j;k*=pri[i]) (f[j]+=f[j-k]*k%mod)%=mod;
		}
	}
	int ans=0;
	for(int j=0;j<=n;j++) (ans+=f[j])%=mod;
	printf("%lld\n",ans);
	return 0;
}

36.P6570 [NOI Online #3 提高组] 优秀子序列

一个数的二进制表示可以看成是一个集合。
设 $dp[i]$ 表示选出若干个互不相交的集合使他们的并为 $i$ 的方案数,则答案是 $\sum dp[i] \times \phi(i+1)$。因为互不相交，所以他们的和也就等于他们的并等于 $i$。

我们先认为原序列没有 $0$。
$dp[i]=∑dp[i \oplus j]*cnt[j]$ ($j$ 是 $i$ 的子集，$cnt[j]$ 表示原序列 $j$ 出现的次数)。为了避免重复计算，当 $j < i \oplus j$ (补集) 时就退出。

对于有 $0$ 的情况，我们往里面可以塞任意多个 $0$ , 所以最后 $dp[i]=dp[i] \times 2^{cnt[0]}$。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int M=1e6+5,N=(1<<18)+5,mod=1e9+7;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,a[M];
int pri[N],tot;
bool stater[N];
int mn[N],mx[N],k[N],phi[N];
/*
	mn[i]:i的最小质因子
	mx[i]:i中所含 mn[i] 的最大幂
	k[i]:i中所含 mn[i] 的个数，mx[i]=mn[i]^k[i] 
	phi[i]:i的欧拉函数 
*/
void Eular()
{
	stater[1]=1;
	phi[1]=1;
	for(int i=2;i<N;i++)
	{
		if(!stater[i]) pri[++tot]=i,mn[i]=i,mx[i]=i,k[i]=1,phi[i]=i-1;
		for(int j=1;j<=tot&&i*pri[j]<N;j++)
		{
			int x=i*pri[j];
			stater[x]=true;
			mn[x]=pri[j];
			if(i%pri[j]==0)
			{
				mx[x]=mx[i]*pri[j];
				k[x]=k[i]+1;
				if(x!=mx[x]) phi[x]=phi[x/mx[x]]*phi[mx[x]];
				else phi[x]=x/mn[x] * (mn[x]-1);    
				/*
					phi(p^k) = p^k - p^(k-1)
							 = p^(k-1) * (p-1)
				*/
				break;
			}
			else
			{
				mx[x]=pri[j];
				k[x]=1;
				phi[x]=phi[i]*phi[pri[j]];
			}
		}
	}
}
int quick_power(int a,int b){
	int ans=1;
	while(b){
		if(b&1) (ans*=a)%=mod;
		(a*=a)%=mod,b>>=1;
	}
	return ans;
}
int Max(int m,int x){
	for(int i=x;i;i-=(i&-i)){
		m=max(m,(int)log2(i&-i));
	}
	return m;
}
int cnt[M],f[M];
signed main(){
	Eular();
	n=read();
	int m=0;
	for(int i=1;i<=n;i++) a[i]=read(),m=Max(m,a[i]),cnt[a[i]]++;
	m++;
	
	f[0]=1;
	for(int i=1;i<(1<<m);i++){
		for(int s=i;s>=(i^s);s=(s-1)&i){
			(f[i]+=f[i^s]*cnt[s]%mod)%=mod;
		}
	} 
	
	int ans=0;
	for(int i=0;i<(1<<m);i++) (f[i]*=quick_power(2,cnt[0]))%=mod;
	for(int i=0;i<(1<<m);i++) (ans+=f[i]*phi[i+1]%mod)%=mod;
	printf("%lld\n",ans);
	return 0;
}

37.CF1280D Miss Punyverse

考虑树形DP。
把每个点的点权 $a[i]$ 设为 $w[i]-b[i]$，
这样只要看 $a$ 之和是否 $>0$。

$f[u][i]$ 表示 $u$ 这棵子树，分成 $i$ 个连通块,不算包含 $u$ 的那一块，最大的 $>0$ 的连通块数,这样不是很转移的动，因为在合并时我们需要知道包含 $u$ 的那一块的权值之和。
考虑贪心，我们会发现有两种比较理想的情况:

不算包含 $u$ 的那一块，其余块中满足条件的块记为 $cnt$,$cnt$ 尽可能大。
包含 $u$ 的那一块，目前的权值记为 $val$,$val$ 尽可能大。

事实上，肯定是按照第一种情况贪心更优，因为第二种情况里，$u$ 的那一块权值再大也不过带来 $1$ 的贡献，无法弥补第一种情况带来的贡献差。

用pair来存储两种情况，$f[u][i].fi=cnt, f[u][i].se=val$。
我们只需要首先让 $cnt$ 尽可能大，其次才是让 $val$ 尽可能大。
边界显然是 $f[u][1]={0,a[u]}$。
每次新加入一个子节点 $v$, 我们有转移:

包含 v 的那一块单独成一个连通块: $f[u][i+j].fi=f[v][j].fi+f[u][i].fi+(f[v][j].se > 0)，f[u][i+j].se=f[u][i].se$。
转移时要优先按照第一维取max(pair自己内部就是这样取max的，不用特殊处理) 。
包含 $v$ 的那一块合进包含 $u$ 的那一块: $f[u][i+j-1].fi=f[v][j].fi + f[u][i].fi ，f[u][i+j-1].se=f[v][j].se + f[u][i].se$。

为了防止转移时用的 f 数组被更新过了，可以开一个辅助数组暂存,也可以倒序枚举。

这个问题其实就是树形背包，但是由于这是动态规划题单系列第一道树形背包题，所以简要讲一下:
对于一个状态 $f[u][i]$ 相当于有一个容积为 $i$ 的背包，每一个子节点 $v$ 对应着一组物品，第 $j$ 个物品大小为 $j$,价值为 $f[v][j]$,每组物品只能选一个(因为只能选一个转移)，使得在不超过背包总体积的情况下(当然这道题因为转移有点特殊其实不一定背包体积是 $i$)，价值的和(这道题里不是简单相加)最大，即分组背包问题。
对于复杂度的分析虽然看起来有点像是 $O(n^3)$,
但注意到一次转移我们其实可以认为是枚举了任意两个子树的大小，也可以认为是分别枚举了两棵子树内的点，一个点对最多只会在 $lca$ 处产生一个复杂度的贡献，一共有 $n^2$ 个点对，所以复杂度为 $O(n^2)$。

code

#include<bits/stdc++.h>
typedef long long ll; 
#define PII pair<int,ll>
#define fi first
#define se second 
using namespace std;
const int N=3e3+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int T;
int n,m;
ll a[N];
int tot,head[N],to[N<<1],Next[N<<1];
void add(int u,int v){
	to[++tot]=v,Next[tot]=head[u],head[u]=tot;
} 
int Size[N];
PII f[N][N],tmp[N];
void dfs(int u,int fa){
	Size[u]=1;
	for(int i=0;i<=n;i++) f[u][i]={INT_MIN,INT_MIN};
	f[u][1]={0,a[u]};
	for(int i=head[u];i;i=Next[i]){
		int v=to[i];
		if(v==fa) continue;
		dfs(v,u);
		for(int j=1;j<=Size[u]+Size[v];j++) tmp[j]={INT_MIN,INT_MIN};
		for(int j=1;j<=min(m,Size[u]);j++){    //不要用填表法，会 TLE 
			for(int k=1;k<=min(m,Size[v]);k++){
				tmp[j+k]=max(tmp[j+k],{f[v][k].fi+f[u][j].fi+(f[v][k].se>0),f[u][j].se});
				tmp[j+k-1]=max(tmp[j+k-1],{f[v][k].fi+f[u][j].fi,f[v][k].se+f[u][j].se});
			}
		}
		for(int j=1;j<=Size[u]+Size[v];j++) f[u][j]=tmp[j];
		Size[u]+=Size[v];
	}
//	cout<<u<<':'<<'\n';
//	for(int i=1;i<=Size[u];i++){
//		cout<<i<<':'<<f[u][i].fi<<','<<f[u][i].se<<'\n';
//	}
}
void Init(){
	tot=0;;
	for(int i=1;i<=n;i++) head[i]=0,a[i]=0;
}
signed main(){
	T=read();
	while(T--){
		n=read(),m=read();
		Init();
		for(int i=1;i<=n;i++){
			ll b=read();
			a[i]-=b;
		}
		for(int i=1;i<=n;i++){
			ll w=read();
			a[i]+=w;
		}
		for(int i=1;i<n;i++){
			int u=read(),v=read();
			add(u,v),add(v,u);
		}
		dfs(1,0);
		printf("%d\n",f[1][m].fi+(f[1][m].se>0));
	}
	return 0;
}

38.CF1500D Tiles for Bathroom

注意到答案是单调的，一个大正方形里的小正方形都满足
为了避免重复，我们对每个右下角统计答案。

考虑计算出 $f[i][j]$ 表示以 $(i,j)$ 为右下角，最大的合法正方形。

考虑从 $f[i-1][j-1]$ 的继承过来，同时会新增第 $i$ 行和第 $j$ 列的贡献。

因为 $q$ 很小，我们完全可以记录对应的合法正方行里，每个颜色出现的最远的位置(这个距离定义为切比雪夫距离，即 $\max(xi-xj,yi-yj)$ )。
所以为了方便更新，我们维护三个队列:

$left[i][j]$: $(i,j)$左边前 $q+1$ 个颜色的位置(同一种颜色取切比雪夫距离最小的,下同)
$up[i][j]$: $(i,j)$上边前 $q+1$ 个颜色的位置
$lu[i][j]$: $(i,j)$左上方(即$1 \le x \le i,1 \le y \le j$)所有的元素中，前 $q+1$ 个颜色的位置。

$left$ 和 $up$ 的更新很容易，只需要加进来 $(i,j)$ 即可。
看一下 $lu[i][j]$：只需要从 $left[i][j-1]$,$up[i-1][j]$,$lu[i-1][j-1]$,$(i,j)$ 中不断取最小的即可，
维护时要满足三个队列内的元素与 $(i,j)$ 的切比雪夫距离始终单调递增。

计算 $f[i][j]$ 时，如果 $lu[i][j]$ 的个数不超过 $q$,那就是 $f[i][j]=min(i,j)$。
否则 $f[i][j]$ 为 $lu[i][j]$ 的第 $q+1$ 个颜色与 $(i,j)$ 的切比雪夫距离 $-1$。
时间复杂度:$O(n^2 \times q)$。

注意到这题卡空间，所以存位置的时候不要用 $pair$ , 把它变成一个数。
代码有点丑。

code

#include<bits/stdc++.h>
#define PII pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=1505;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,q,a[N][N];
int ans[N]; 
int PairToNum(PII u){   //把坐标 (x,y) 变成数字 
	return (u.fi-1)*n+(u.se-1); 
}
PII NumToPair(int pos){ //把数字 变成 坐标
	return {pos/n+1,pos%n+1};
}
struct Queue{
	int q[12]; 
	int head=0,tail=-1;
	bool empty(){return tail<head;}
	void push(PII x){
		q[++tail]=PairToNum(x);
	}
	void pop(){
		++head;
	}
	void pop_back(){
		--tail;
	}
	PII front(){
		if(empty()) return {0,0}; 
		return NumToPair(q[head]);
	}
	int size(){return tail-head+1;};
}L[N][N],U[N][N],LU[N][N];
int calc(PII u,PII v){   //计算切比雪夫距离(真正的是不用+1的，这里要计算正方形边长所以加一))
	return max(abs(u.fi-v.fi),abs(u.se-v.se))+1;
}

bool flag[N*N];
signed main(){
	n=read(),q=read();
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			a[i][j]=read();
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			L[i][j].push({i,j});
			for(int k=L[i][j-1].head;k<=L[i][j-1].tail;k++){
				PII u=NumToPair(L[i][j-1].q[k]);
				if(a[u.fi][u.se]==a[i][j]) continue;;
				L[i][j].push(u);
			}
			if(L[i][j].size()>q+1) L[i][j].pop_back();
			
			U[i][j].push({i,j});
			for(int k=U[i-1][j].head;k<=U[i-1][j].tail;k++){
				PII u=NumToPair(U[i-1][j].q[k]);
				if(a[u.fi][u.se]==a[i][j]) continue;;
				U[i][j].push(u);
			}
			if(U[i][j].size()>q+1) U[i][j].pop_back();
			
			LU[i][j].push({i,j});
			flag[a[i][j]]=true;   //记录这种颜色是否出现过 
			int t1=L[i][j-1].head,t2=U[i-1][j].head,t3=LU[i-1][j-1].head;
			while(LU[i][j].size()<=q && (!L[i][j-1].empty() || !U[i-1][j].empty() || !LU[i-1][j-1].empty())){
				PII u=L[i][j-1].front(),v=U[i-1][j].front(),w=LU[i-1][j-1].front();
				 
				int d1=calc(u,{i,j}),d2=calc(v,{i,j}),d3=calc(w,{i,j}),mind=min({d1,d2,d3});   //取最小的那一个 
				if(mind==d1 && !L[i][j-1].empty()){
					L[i][j-1].pop();
					if(flag[ a[u.fi][u.se] ]) continue;  //出现过就忽略了 
					LU[i][j].push(u);
					flag[ a[u.fi][u.se] ]=true;	
				} 
				else if(mind==d2 && !U[i-1][j].empty()){
					U[i-1][j].pop();
					if(flag[ a[v.fi][v.se] ]) continue;
					LU[i][j].push(v);
					flag[ a[v.fi][v.se] ]=true;
				} 
				else{
					LU[i-1][j-1].pop();
					if(flag[ a[w.fi][w.se] ])continue;
					LU[i][j].push(w);
					flag[ a[w.fi][w.se] ]=true;
				}
			}
			L[i][j-1].head=t1,U[i-1][j].head=t2,LU[i-1][j-1].head=t3;
			for(int k=LU[i][j].head;k<=LU[i][j].tail;k++){
				PII u=NumToPair( LU[i][j].q[k] );
				flag[a[u.fi][u.se]]=false;
			} 
			
			int tmp=min(i,j);
			if(LU[i][j].size()==q+1) tmp=min(tmp,calc( NumToPair(LU[i][j].q[LU[i][j].tail]) , {i,j} )-1); 
			ans[tmp]++;
		} 
	}
	
	for(int i=n;i>=1;i--) ans[i]+=ans[i+1];
	for(int i=1;i<=n;i++) printf("%d\n",ans[i]);
	return 0;
}

39.CF1276D Tree Elimination

神仙分类讨论树形DP题，按照连向父亲的边什么时候被删的分类讨论一下，因为 LaTex 打起来太烦了，所以具体看题解区的吧。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=2e5+5,mod=998244353;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n;
vector<int> G[N];  //vector存边天然优势:编号大的在后面 
int f[N][4],pre[N],suf[N];
void dfs(int u,int fa){
	bool flag=false;  //编号是否比 (u,fa) 大 
	f[u][1]=f[u][3]=1;
	for(int v:G[u]){
		if(v==fa){
			flag=true;
			continue;
		} 
		dfs(v,u);
		(f[u][3]*=(f[v][0]+f[v][1])%mod)%=mod;
		if(!flag){
			(f[u][1]*=(f[v][0]+f[v][1])%mod)%=mod;  //此时 u 还在 
		}
		else{
			(f[u][1]*=(f[v][0]+f[v][2]+f[v][3])%mod)%=mod;   //此时 u 已经没了
		}
	}
	pre[0]=1;
	for(int i=1;i<=G[u].size();i++){
		int v=G[u][i-1];
		if(v==fa){
			pre[i]=pre[i-1];
			continue;
		}
		(pre[i]=pre[i-1]*(f[v][0]+f[v][1])%mod)%=mod;
	}
	suf[G[u].size()+1]=1;
	for(int i=G[u].size();i>=1;i--){
		int v=G[u][i-1];
		if(v==fa){
			suf[i]=suf[i+1];
			continue;
		}
		(suf[i]=suf[i+1]*(f[v][0]+f[v][2]+f[v][3])%mod)%=mod;
	}
	f[u][0]=f[u][2]=0;
	flag=false;
	for(int i=1;i<=G[u].size();i++){
		int v=G[u][i-1];
		if(v==fa){
			flag=true;
			continue;
		} 
		if(!flag){
			(f[u][0] += (f[v][2]+f[v][3])%mod * pre[i-1]%mod * suf[i+1]%mod)%=mod; 
		}
		else{
			(f[u][2] += (f[v][2]+f[v][3])%mod * pre[i-1]%mod * suf[i+1]%mod)%=mod;  
		}
	}
	
}
signed main(){
	n=read();
	for(int i=1;i<n;i++){
		int u=read(),v=read();
		G[u].push_back(v),G[v].push_back(u);
	}
	dfs(1,0);
	printf("%lld\n",(f[1][0]+f[1][2]+f[1][3])%mod);
	return 0;
}

40.P1081 [NOIP2012 提高组] 开车旅行

经典倍增优化DP题。

预处理:
$a[i],b[i]$ 分别表示 $A/B$ 开车从 $i$ 开始，下一个到达的城市。
用 multiset 维护即可，不赘述
DP:

$f[i][j][k]$ 表示行驶 $2^i$ 天，从城市 $j$ 开始，$k$ 先开车会到的城市。
$sa[i][j][k]$ 表示行驶 $2^i$ 天，从城市 $j$ 开始，$k$ 先开车,小A开的距离。
$sb[i][j][k]$ 表示行驶 $2^i$ 天，从城市 $j$ 开始，$k$ 先开车,小B开的距离。
注意当 $i=0$ 时，$2^0=1$为奇数，转移时要注意开车的人会变。其余就正常的转移

calc函数：
$calc(s,x)$ 表示从 $s$ 开始，最多行驶 $x$,小A和小B分别会行驶的距离,倍增即可
回答询问:
询问一:只会问一次，暴力枚举起点。
询问二:直接输出 $calc(si,xi)$。

code

#include<bits/stdc++.h>
#define PII pair<int,int>
#define fi first
#define se second
#define int long long 
using namespace std;
const int N=1e5+5,M=(1<<17)+5,inf=2e14;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,h[N];

int a[N],b[N];
multiset<PII> s;
multiset<PII>::iterator it1,it2; 
int dist(int x,int y){
	if(x==0||y==0) return inf;
	return abs(h[x]-h[y]);
}
int u;
bool cmp1(PII x,PII y){
	if(dist(x.se,u)==dist(y.se,u)) return x.fi<y.fi;
	return dist(x.se,u)<dist(y.se,u);
}
void Init(){
//	return;
	s.insert({inf,0}),s.insert({inf,0}),s.insert({-inf,0}),s.insert({-inf,0});
	//防止越界 
	for(int i=n;i>=1;i--){
		PII tmp[6];
		s.insert({h[i],i});
		it1=it2=s.find({h[i],i});
		--it1; tmp[1]=*it1;
		--it1; tmp[2]=*it1;
		++it2; tmp[3]=*it2;
		++it2; tmp[4]=*it2;
		u=i;
		sort(tmp+1,tmp+4+1,cmp1);
		a[i]=tmp[2].se,b[i]=tmp[1].se;
	}
}


int f[20][N][2],sa[20][N][2],sb[20][N][2];
void DP(){
	for(int i=1;i<=n;i++){
		f[0][i][0]=a[i],f[0][i][1]=b[i];
		sa[0][i][0]=dist(i,a[i]),sa[0][i][1]=0;
		sb[0][i][1]=dist(i,b[i]),sb[0][i][0]=0;
	}
	for(int i=1;i<=17;i++){
		for(int j=1;j<=n;j++){
			for(int k=0;k<=1;k++){
				if(i==1){
					f[i][j][k]=f[i-1][ f[i-1][j][k] ][1-k];
					sa[i][j][k]=sa[i-1][j][k] + sa[i-1][ f[i-1][j][k] ][1-k];
					sb[i][j][k]=sb[i-1][j][k] + sb[i-1][ f[i-1][j][k] ][1-k];
				}
				else{
					f[i][j][k]=f[i-1][ f[i-1][j][k] ][k];
					sa[i][j][k]=sa[i-1][j][k] + sa[i-1][ f[i-1][j][k] ][k];
					sb[i][j][k]=sb[i-1][j][k] + sb[i-1][ f[i-1][j][k] ][k];
				}
			}
		}
	}
}

PII calc(int s,int x){
	int suma=0,sumb=0,sum=0;
	for(int i=17;i>=0;i--){
		if(f[i][s][0]&&(sum+sa[i][s][0]+sb[i][s][0])<=x){
			suma+=sa[i][s][0],sumb+=sb[i][s][0],sum=suma+sumb;
			s=f[i][s][0];
		}
	}
	return {suma,sumb};
}

struct frac{
	int a,b,id;
};
bool cmp(frac x,frac y){
	if(x.b==y.b&&x.b==0) return h[x.id]>h[y.id];
	if(y.b==0) return true;
	if(x.b==0) return false;
	if(x.a*y.b==y.a*x.b) return h[x.id]>h[y.id];
	return x.a*y.b<y.a*x.b;
}
void solve1(){
	int x0=read();
	frac ming={1,0,0};
	for(int i=1;i<=n;i++){
		int s1=calc(i,x0).fi,s2=calc(i,x0).se;
		if(cmp({s1,s2,i},ming)) ming={s1,s2,i};
	}	
	printf("%lld\n",ming.id);
}

void solve2(){
	int T=read();
	while(T--){
		int s=read(),x=read();
		printf("%lld %lld\n",calc(s,x).fi,calc(s,x).se);
	}
}
signed main(){
	n=read();
	h[0]=-inf;
	for(int i=1;i<=n;i++) h[i]=read();
	Init();
	DP();
	solve1();
	solve2();
	return 0;
}

41.P9197 [JOI Open 2016] 摩天大楼

~~其实这个在动态规划题单一应该就要写了，但是太懒了，所以拖到现在。~~

套路和 [CEOI2016] kangaroo 有点类似(在第一个题单里)，所以建议先看那题。
那我们先列出状态: $f[i][j][k][0/1][0/1]$ 表示从大到小放到第 $i$ 个数，一共有 $j$ 个连续段，题目里的式子计算结果为 $k$,放/没放第一个，放/没放最后一个的方案数。
但这样如果我们每一次新放进来一个数，只是计算他和他两边的数新增的贡献，我们还需要记录整个序列的哪些位置填了哪些数，才能转移动 $k$,但这样状态就炸了。所以我们考虑转换一下计算 $|f_1-f_2| + |f_2-f_3| +...+ |f_{N-1}-f_N|$ 的计算方法。

假如最后是这么个填数方案，横坐标是下标，纵坐标是数值。

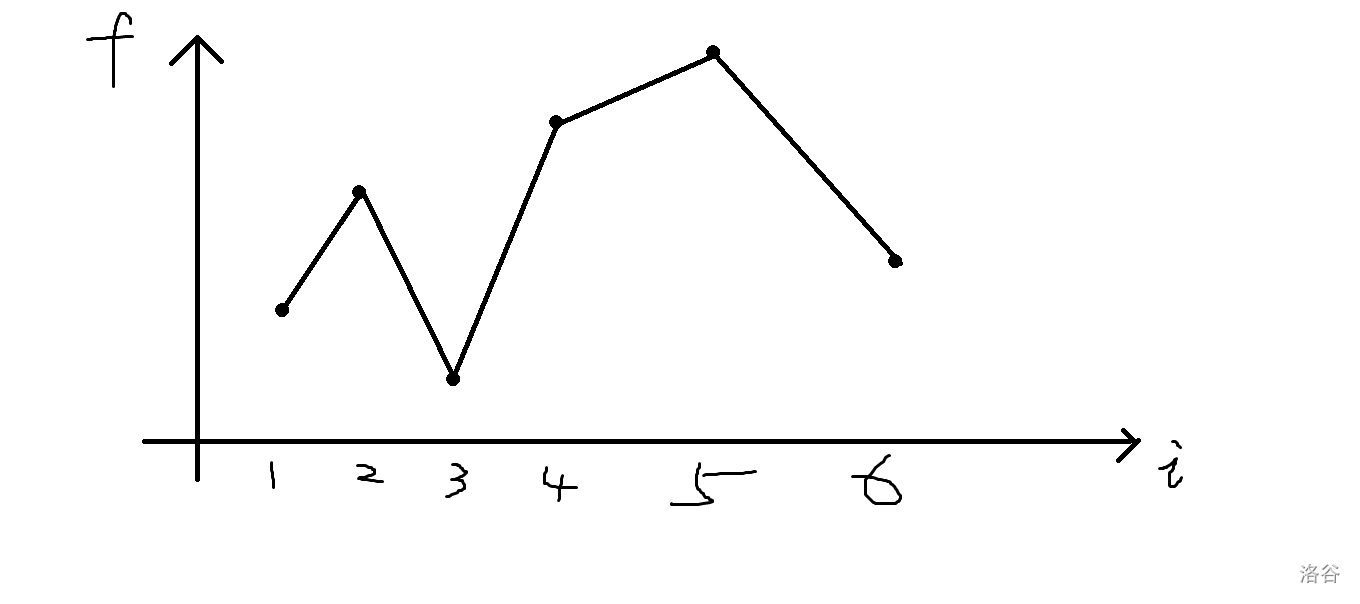
所以当我们从大到小填到第四个数的时候(即图中的$f_6$),我们按照原始的方法其实只计算了图中绿色的线段的值。

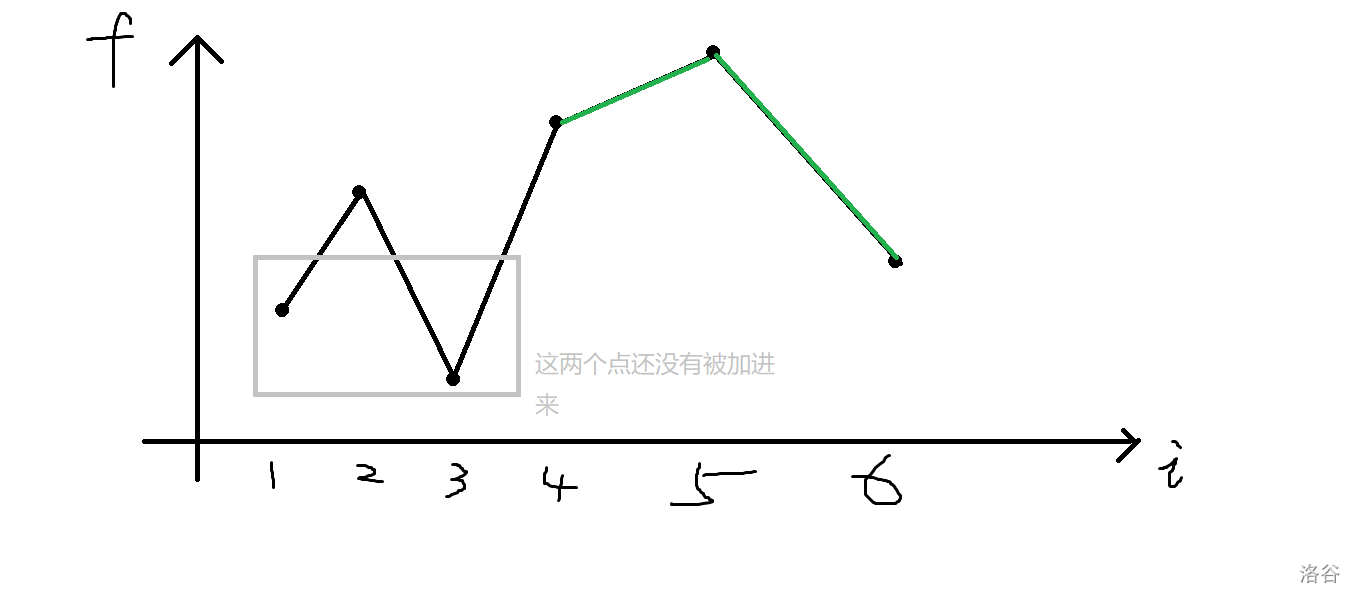
这就使得我们再加进第五个点的时候很不好计算多出来的答案，所以我们计算答案的方式变为:
当新放进来一个数 $a_i$ 时，假设现在的段数是 $j$,那么把答案累加上 $(a_{i-1}-a_i) \times (2j)$,意思是每一段自动在两侧延申 $(a_{i-1}-a_i)$,也可以看作是提前计算贡献。

这样当我们从大到小填到第四个数的时候,我们其实就计算了图中蓝色部分的线段了。

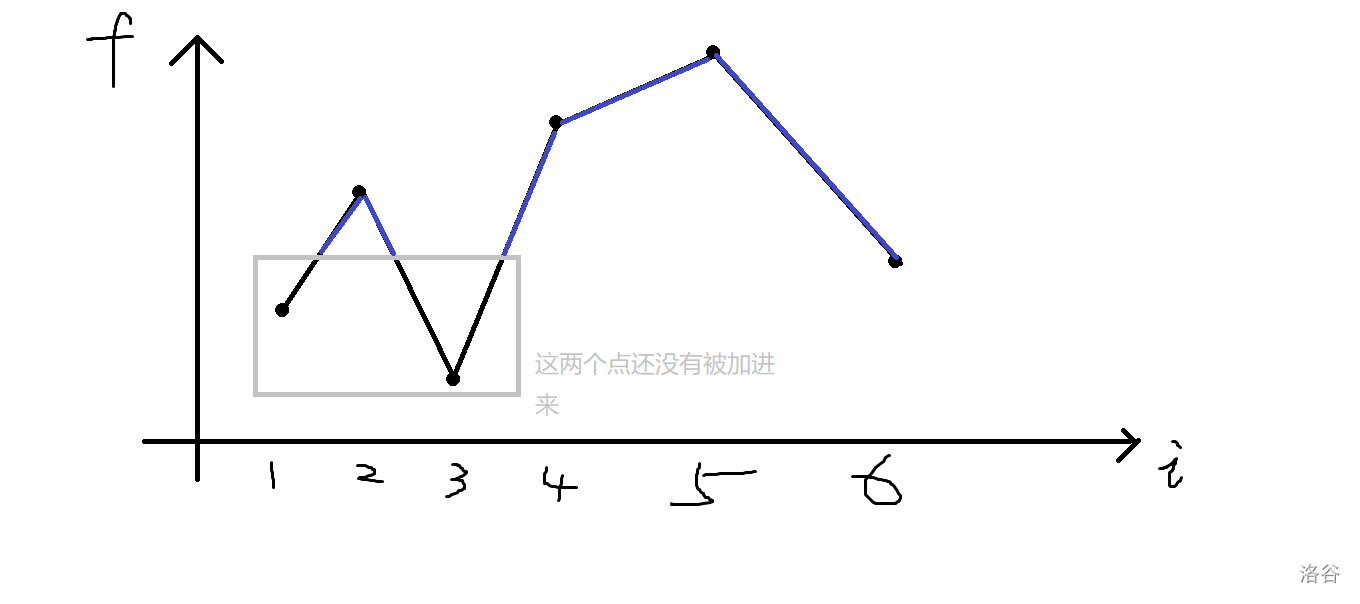
但这样还是会有个小问题，就是在加第$5$个点时，按照上述算法，多出来的答案是图中红色加上黄色线段。
但其实黄色线段是没有的。

解决办法也比较简单，在开头和结尾已经放了的情况下转移特判一下即可。

具体细节见代码。

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5,mod=1e9+7;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,L,a[105];
int f[105][105][1005][2][2];
/*
	f[i][j][k][0/1][0/1]表示从大到小放到第 i 个数，一共有j个连续段，题目里的式子计算结果为 k,放/没放第一个，放/没放最后一个 
*/
signed main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	n=read(),L=read();
	for(int i=1;i<=n;i++) a[i]=read();
	if(n==1){
		cout<<1<<'\n';
		return 0;   // 此时它又是开头，又是结尾 
	}
	sort(a+1,a+n+1,greater<int>());
	
	f[0][0][0][0][0]=1; 
	for(int i=0;i<=n;i++){
		for(int j=0;j<=i;j++){
			for(int k=0;k<=L;k++){
				int sum;  //新增贡献
				 
				//从f[i][j][k][0][0]转移
				sum=k + 2 * j * (a[i] - a[i+1]);
				if(sum<=L&&sum>=0){
					//1.i+1放开头
					( f[i + 1][j + 1][sum][1][0] += f[i][j][k][0][0] ) %= mod;   //自成一段 
					( f[i + 1][j][sum][1][0] += f[i][j][k][0][0] ) %= mod;     //粘在一段前面 
					//2.i+1放结尾
					( f[i + 1][j + 1][sum][0][1] += f[i][j][k][0][0] ) %= mod;   //自成一段 
					( f[i + 1][j][sum][0][1] += f[i][j][k][0][0] ) %= mod;     //粘在一段后面 
					//3.i+1放中间
		 			( f[i + 1][j + 1][sum][0][0] += (j + 1) * f[i][j][k][0][0] % mod ) %= mod; //自成一段 
					( f[i + 1][j][sum][0][0] += 2 * j * f[i][j][k][0][0] % mod ) %= mod;  //粘在一段前面/后面
					( f[i + 1][j - 1][sum][0][0] += (j - 1) * f[i][j][k][0][0] % mod) %= mod;  //把两段粘在一起 
				}
				
				//从f[i][j][k][1][0]转移 
				sum=k + (2 * j - 1) * (a[i] - a[i+1]);
				if(sum<=L&&sum>=0){
					//1.i+1放结尾
					( f[i + 1][j + 1][sum][1][1] += f[i][j][k][1][0] ) %= mod;   //自成一段 
					( f[i + 1][j][sum][1][1] += f[i][j][k][1][0] ) %= mod;     //粘在一段后面
					//2.i+1放中间,不能放开头了 
		 			( f[i + 1][j + 1][sum][1][0] += j * f[i][j][k][1][0] % mod ) %= mod; //自成一段 
					( f[i + 1][j][sum][1][0] += (2 * j - 1) * f[i][j][k][1][0] % mod ) %= mod;  //粘在一段前面/后面
					( f[i + 1][j - 1][sum][1][0] += (j - 1) * f[i][j][k][1][0] % mod) %= mod;  //把两段粘在一起
				}
				
				//从f[i][j][k][0][1]转移
				sum=k + (2 * j - 1) * (a[i] - a[i+1]);
				if(sum<=L&&sum>=0){
					//1.i+1放开头
					( f[i + 1][j + 1][sum][1][1] += f[i][j][k][0][1] ) %= mod;   //自成一段 
					( f[i + 1][j][sum][1][1] += f[i][j][k][0][1] ) %= mod;     //粘在一段前面 
					//2.i+1放中间,不能放结尾了 
		 			( f[i + 1][j + 1][sum][0][1] += j * f[i][j][k][0][1] % mod ) %= mod; //自成一段 
					( f[i + 1][j][sum][0][1] += (2 * j - 1) * f[i][j][k][0][1] % mod ) %= mod;  //粘在一段前面/后面
					( f[i + 1][j - 1][sum][0][1] += (j - 1) * f[i][j][k][0][1] % mod) %= mod;  //把两段粘在一起	
				}
				
				//从f[i][j][1][1]转移
				sum=k + (2 * j - 2) * (a[i] - a[i+1]);
				if(sum<=L&&sum>=0){
					//1.i+1放中间,不能放开头和结尾了 
		 			( f[i + 1][j + 1][sum][1][1] += (j - 1) * f[i][j][k][1][1] % mod ) %= mod; //自成一段 
					( f[i + 1][j][sum][1][1] += (2 * j - 2) * f[i][j][k][1][1] % mod ) %= mod;  //粘在一段前面/后面
					( f[i + 1][j - 1][sum][1][1] += (j - 1) * f[i][j][k][1][1] % mod) %= mod;  //把两段粘在一起	
				}
			}
		}
	} 
	
	int ans=0;
	for(int i=0;i<=L;i++){
		(ans += f[n][1][i][1][1]) %= mod;
	}
	printf("%lld\n",ans);
	return 0;
}

42.Count The Repetitions*

$[S2，M]=[s2,n2*M]$。
找到最大的 $M$ 也就是找到最大的 $M'$ 使得 $[S2,M']$ 是 $[s1,n1]$ 的子序列。答案那就是 $\lfloor \frac {M'} {n2} \rfloor$ 。

无解的判定:如果 $s2$ 中的字符没有全部在 $s1$ 中出现就无解。否则至多重复 $s1$ $len2$ 次就可以得到一个 $s2$ ($len2$ 是 $s2$ 的长度)。

预处理:$g[i]$ 表示从 $s1$ 的第 $i$ 位开始，至少接需要多少个字符才能凑出一个 $s2$，注意不是接多少个 $s1$,而是字符,$O(len^3)$ 暴力即可

设 $f[i][s]$ 表示从 $s1$ 的第 $s$ 个开始,凑出 $2^i$ 个 $s2$ 需要多少个字符,转移显然。

倍增优化求答案的过程即可。

code


#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
char s1[105],s2[105];
int n1,n2,len1,len2;
int g[105],f[40][105];
bool stater;
void Init(){
	memset(g,0x3f,sizeof g);
	memset(f,0x3f,sizeof f);
	len1=strlen(s1),len2=strlen(s2);
	stater=true;
	string s;
	for(int i=1;i<=len2;i++) s=s+s1;
	for(int i=0;i<len1;i++){
		int k=0;
		for(int j=i,cnt=1;j<s.size();j++,cnt++){
			if(s[j]==s2[k]){
				k++;
				if(k==len2){
					g[i]=cnt;
					break;
				}
			}
		}
		if(g[i]>s.size()){
			stater=false;
			return;
		}
		else f[0][i]=g[i];
	}
	for(int t=1;t<=30;t++){
		for(int i=0;i<len1;i++){
			f[t][i]=f[t-1][i]+f[t-1][(i+f[t-1][i])%len1];
		}
	}
}
void work(){
	if(!stater){
		puts("0");
		return;
	}
	int maxn=len1*n1,sum=0,res=0,pos=0;
	for(int i=30;i>=0;i--){
		if(f[i][pos]+sum<=maxn){
			sum+=f[i][pos];
			pos=(pos+f[i][pos])%len1;
			res+=pow(2,i);
		}
	}
	printf("%lld\n",res/n2);
}
signed main(){
	 while(scanf("%s %lld\n%s %lld",s2,&n2,s1,&n1)==4){
		Init();
		work();
	}
	return 0;
}

43.CF1788E Sum Over Zero

$f[i]$:表示区间 $[1,i]$ 上的最大值 (一定要选 $i$)。
$pre[i]$:表示 $max{f[0],f[2],...,f[i]}$。
$s[i]=a1+a2+...+ai$。

转移:$f[i]=max_{0 \le j \le i-1,si-sj \ge 0}({i-j+pre[j]})$

$f[i]$ 转移的优化:在每个 $s[j]$ 上记录最大的 $pre[j]-j$ , 转移时在线段树上查询 $(-inf,si]$ 的最大值。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=2e5+5,MAXN=2e14;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,a[N];
int s[N],pre[N],f[N];
int dis[N],m;
int Dis(int x){
	return lower_bound(dis+1,dis+m+1,x)-dis; 
}
struct node{
	int l,r,maxn;
};
struct SegmentTree{
	node t[10000005];
	void pushup(int p){
		t[p].maxn=max(t[p<<1].maxn,t[p<<1|1].maxn);
	}
	void build(int p,int l,int r){
		t[p].l=l,t[p].r=r,t[p].maxn=LLONG_MIN;
		if(l==r) return;
		int mid=(l+r)>>1;
		build(p<<1,l,mid);
		build(p<<1|1,mid+1,r);
		pushup(p);
	}
	void change(int p,int x,int val){
		if(t[p].l==t[p].r){
			t[p].maxn=max(t[p].maxn,val);
			return;
		}
		int mid=(t[p].l+t[p].r)>>1;
		if(x<=mid){
			change(p<<1,x,val);
		}
		else{
			change(p<<1|1,x,val);
		}
		pushup(p);
	}
	int ask(int p,int l,int r){
		if(l<=t[p].l&&t[p].r<=r){
			return t[p].maxn;
		}	
		int mid=(t[p].l+t[p].r)>>1,res=LLONG_MIN;
		if(l<=mid) res=max(res,ask(p<<1,l,r));
		if(r>mid) res=max(res,ask(p<<1|1,l,r));
		return res;
	}
}Seg;
signed main(){
	int ming=0;
	n=read();
	dis[n+1]=0;
	for(int i=1;i<=n;i++) a[i]=read(),s[i]=s[i-1]+a[i],dis[i]=s[i],ming=min(ming,s[i]);
	sort(dis+1,dis+n+1+1);
	m=unique(dis+1,dis+n+1+1)-dis-1; 
	
	Seg.build(1,1,m);
	f[0]=0;
	pre[0]=0;
	Seg.change(1,Dis(s[0]),pre[0]);
	for(int i=1;i<=n;i++){
		f[i]=Seg.ask(1,Dis(ming),Dis(s[i]))+i;
		pre[i]=max(pre[i-1],f[i]);
		Seg.change(1,Dis(s[i]),pre[i]-i);
	}
	printf("%lld\n",pre[n]);
	return 0;
}

44.CF1799D2 Hot Start Up (hard version)

压缩状态优化DP 。

$f[i][x][y]$ 表示处理完第 $i$ 个程序，目前第一个 CPU 里运行的程序种类是 $x$,第二个里运行的程序种类是 $y$。
因为 $x,y$ 中一定有一个是 $ai$,考虑把第一维去掉，那么有转移(很明显能用 $hot$ 就不用 $cold$):

$f[x][y]+cold[ai] \to f[ai][y]$
$f[x][y]+cold[ai] \to f[x][ai]$
$f[x][ai]+hot[ai] \to f[x][ai]$
$f[ai][x]+hot[ai] \to f[ai][x]$

直接跑是 $O(n\times k^2)$ 的

我们会发现每次转移时，都只会转移到 $f[ai][x]$ 或 $f[x][ai]$。同理在进行转移的时候也只有 $f[a[i-1]][x]$ 和 $f[x][a[i-1]]$ 中会有值。只需要枚举 $x$ ,进行转移即可。

因为两个 CPU 本质相同,所以 $f[x][y]$ 显然等于$f[y][x]$，即转移优化成: (默认 $a[i-1] \ne a[i]$，如果相等直接全部加 $hot[ai]$ 即可)

$f[a[i-1]][x]+cold[ai] \to f[a[i-1]][ai]$ (此时如果 $x=ai$ 的话，肯定不如第3条优)
$f[a[i-1]][x]+cold[ai] \to f[ai][x]$
$f[a[i-1]][ai]+hot[ai] \to f[a[i-1]][ai]$

可以通过简单版。

还是因为 $f[x][y]=f[y][x]$,所以转移到 $f[ai][x]$ 和转移到 $f[x][ai]$ 是一样的，所以我们考虑进一步压缩状态用 $f[x]$ 代替 $f[ai][x]$，那么上面那三个转移式子就优化成:

如果 $a[i-1] \ne ai$

$f[x]+cold[ai] \to f[a[i-1]]$
$f[x]+cold[ai] \to f[x]$
$f[ai]+hot[ai] \to f[a[i-1]]$

分别进行优化:

转移到的目标是定的，直接维护全局最小值进行转移即可。
相当于每个点都加一个 $cold[ai]$,我们用 $add$ 记录一下全局累加标记即可。
下标都给定了，直接转移。

如果 $a[i-1]=ai$,直接 $add+=hot[ai]$。

几个注意:

如果进行了转移1或3，那此时是不用加上转移2的 $cold[ai]$ 的，要先减掉 $cold[ai]$。
维护新的全局最小值时全部重新跑一遍肯定不太对，我们会发现这三个转移中只有转移二会转移到 $f[x]$,但是 $f[x]+cold[ai]$ 不仅会转移给 $f[x]$,也会转移给 $f[a[i-1]]$,而 $f[a[i-1]]$ 还可以通过 $f[ai]+hot[ai]$ 转移,所以 $f[a[i-1]]$ 一定是全局最小值，只要用它更新即可。
3.一开始 $f[0]=0$, 其余全是 $inf$。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=3e5+5,inf=3e14+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int T;
int n,k,a[N],cold[N],hot[N],f[N];
void work(){
	n=read(),k=read();
	for(int i=1;i<=n;i++) a[i]=read();
	for(int i=1;i<=k;i++) cold[i]=read(),f[i]=inf;
	for(int i=1;i<=k;i++) hot[i]=read();
	f[0]=0;
	int add=0,ming=0;
	for(int i=1;i<=n;i++){
		if(a[i]!=a[i-1]){
			add+=cold[a[i]];
			f[a[i-1]]=min({f[a[i-1]] , ming+cold[a[i]]-cold[a[i]] , f[a[i]]+hot[a[i]]-cold[a[i]]});
			ming=f[a[i-1]];
		}
		else add+=hot[a[i]];
	}
	printf("%lld\n",ming+add);
}
signed main(){
	T=read();
	while(T--) work();
	return 0;
}

45.CF1304F2 Animal Observation (hard version)

题意简化:给定一个 $n\times m$ 的矩形，每一行选择一个点，并以这个点为左上角框出一个 $2\times k$ 的小矩形,求所有小矩形的并所覆盖的数字之和的最大值。

设 $m'=m-k+1$,显然每个点的纵坐标不会超过 $m'$。

设 $f[i][j]$ 表示第 $i$ 行选第 $j$ 个点，前 $i$ 行的最大值。
如果可以重复，那 DP 方程容易得出:
$f[i][j]=max_{1\le x\le m'}(f[i-1][x]+pre[i][x+k-1]-pre[i][x-1]) + pre[i][j+k-1] - pre[i][j-1]$, $pre[i]$ 是第 $i$ 行的前缀和。
前面一项容易维护，从而 $O(1)$ 转移，总时间复杂度 $O(n^2)$。

考虑去掉重复贡献。
设 $f[i][j]$ 表示第 $i$ 行选第 $j$ 个点，前 $i$ 行的最大值（不能重复贡献）。
又设 $g[i][j]=f[i][j]+pre[i+1][j+k-1]-pre[i+1][j-1]$。
则转移方程可以写成：
$f[i][j]=max_{1\le x \le m'}{g[i-1][x]} + pre[i][j+k-1] - pre[i][j-1] - 重复贡献的部分$。
考虑把重复贡献的部分在 max 里就去掉，一个点 $a[i][y] (j\le y\le j+k-1)$ 重复贡献在:
$g[i-1][y-k+1],...,g[i-1][y-1],g[i-1][y]$。
只需要把他们全部减去 $a[i][y]$ 即可，支持区间减，区间查最大值的是什么? 线段树。转移完之后再加回去。

但这样是 $O(n \times m \times k \times \log m)$,因为要对每个 $j<=y<=j+k-1$ 都做一遍区间减。但是当 $j$ 从 $j$ 变到 $j+1$，其实只有 $j$ 这个位置不再被重复贡献，$j+1+k-1$ 这个位置新加进来，所以就好了。
所以 $O(n\times m\times \log m)$。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=2e4+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,m,k,a[55][N],pre[55][N];
int f[55][N],g[N];
struct node{
	int l,r,maxn,add;
	void tag(int d){
		maxn+=d;
		add+=d;
	}
};
struct SegmentTree{
	node t[N<<2];
	void pushup(int p){
		t[p].maxn=max(t[p<<1].maxn,t[p<<1|1].maxn); 
	}
	void spread(int p){
		if(t[p].add){
			t[p<<1].tag(t[p].add);
			t[p<<1|1].tag(t[p].add);
			t[p].add=0;
		}
	}
	void build(int p,int l,int r){
		t[p].l=l,t[p].r=r,t[p].add=0;    //add也要清空 
		if(l==r){
			t[p].maxn=g[l];
			return;
		}	
		int mid=(l+r)>>1;
		build(p<<1,l,mid);
		build(p<<1|1,mid+1,r);
		pushup(p);
	} 
	void change(int p,int l,int r,int d){
		if(l<=t[p].l&&t[p].r<=r){
			t[p].tag(d);
			return;
		}
		spread(p);
		int mid=(t[p].l+t[p].r)>>1;
		if(l<=mid) change(p<<1,l,r,d);
		if(r>mid) change(p<<1|1,l,r,d);
		pushup(p);
	}
}Seg;

signed main(){
	n=read(),m=read(),k=read();
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			a[i][j]=read();
			pre[i][j]=pre[i][j-1]+a[i][j];
		}
	}
	
	int m1=m-k+1;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m1;j++){
			if(i!=1){
				if(j==1){
					for(int y=j;y<=j+k-1;y++) Seg.change(1,1,y,-a[i][y]);
				}
				else{
					Seg.change(1,max(1ll,j-1-k+1),j-1,a[i][j-1]);
					Seg.change(1,j,j+k-1,-a[i][j+k-1]);
				}
			}
			f[i][j]=Seg.t[1].maxn+pre[i][j+k-1]-pre[i][j-1];
			g[j]=f[i][j]+pre[i+1][j+k-1]-pre[i+1][j-1];
		}
		Seg.build(1,1,m1);
	}
	int ans=0;
	for(int i=1;i<=m1;i++) ans=max(ans,f[n][i]);
	printf("%lld\n",ans);
	return 0;
}

46.夏虫（summer）

题意简述:

用 $n$ 个虫子，每个虫子有一个狡猾值 $a_i$,一开始你会站在一个虫子 $x$ 前，将初始能力值设为 $a_x$，并捕捉它，接下来你可以重复执行三种操作，直到捕捉完所有昆虫:
设当前捕捉到了区间 $[l,r]$ 的昆虫，能力值为 $v$

若 $l \ne 1$ 并且 $a_{l−1} \le v$ ，那么可以花费 $1$ 单位精力捕捉 $l−1$ 号夏虫；
若 $r \ne n$ 并且 $a_{r+1} \le v$ ，那么她们可以花费 $1$ 单位精力捕捉 $r + 1$ 号夏虫；
花费 $k$ ($k$ 是定值)单位精力使得捕虫网的能力值为 $min(a_{l−1}, a_{r+1})$。在这里定义 $a_0 = a_{n+1} = inf$。

有 $Q$ 次询问，每次给定 $x,l,r$ 表示交换 $x,x+1$ 两只昆虫的位置后，询问你初始站在 $[l,r]$ 内的每只昆虫前的最小花费精力的和。注意交换操作是永久的，即会对后面的询问产生影响。

题解:

首先操作 $1$ 和操作 $2$ 肯定加起来要做 $n-1$ 次，所以只需要看操作 $3$ 要几次。
容易用单调栈维护处 $L[i]/R[i]$ 表示 $a[i]$ 作为最大值的区间。
那么设 $f[i]$ 表示以 $i$ 为开始需要多少次操作 $3$,不妨设 $a[L[i]-1] < a[R[i]+1]$,则 $f[i]=f[L[i]-1] + 1$。
所以按照值域从大到小 $dp$ 即可做到 $O(n)$ 求解单次询问，那么时间复杂度 $O(nQ)$,有 40 分。

但是如果按照这种转移的求法，不是很好在每次修改后维护 $f$,考虑换一个求法:
设 $A_x$ 表示 $a[1],a[2],...,a[x]$ 的后缀最大值的集合。$B_x$ 表示 $a[x],a[x+1],...,a[n]$ 的前缀最大值的集合。
那么答案就是 $|A_x \cup B_x| - 1$,-1 是因为 $a[x]$ 自己是不用算的，这个式子应该还好理解，就不证了。

我们维护两棵线段树 $Seg1,Seg2$。$Seg1$ 维护 $a$ 序列，$Seg2$ 维护 $f$ 。
注意:我们是无法去维护 $A,B$ 集合的，即不能对每个数开两个 $multiset$，当然因为无法维护，我们也不需要真的在集合里删掉某些数(这是好的)

假设现在交换了 $a[x],a[x+1]$,去考虑会影响哪些数的 $A,B$ 集合。

$a[x]<a[x+1]$

对于 $1 \le i \le x-1$ 的 $i$,它们的 $A$ 集合显然是不变的，但是 $B$ 集合里有可能原来有 $a[x]$,现在就没了(因为 $a[x+1]$ 跑到 $a[x]$ 前面了)。
首先我们需要知道哪些数的 $B$ 集合原来有 $a[x]$,容易知道一定是 $[l,x-1]$ 这一段区间的数，其中每个数都 $<a[x]$,注意如果 $=a[x]$ 是不算的，因为 $=a[x]$ 的话他的 $B$ 集合里仍然有 $a[x]$。
求这个 $l$ 在 $Seg1$ 上线段树二分即可，但是要知道 $i \in [l,x-1]$ 的 $f[i]$ 是否改变还要看 $A[i]$ 里是否有 $a[x]$，这里不用也不能去每个数判断一遍，注意到对于 $A[i]$,他在 $a[l],a[l+1],..,a[i]$ 的后缀$max$里肯定是没有 $a[x]$ 的，所以只需要去看 $a[l-1]$ 是否 $=a[x]$ 即可。
如果 $a[l-1] \ne a[x]$的话他们的 $f[i]-1$,即在 $Seg2$ 上区间 $-1$。
对于 $i\ge x+2$,他们的 $B$ 集合不变，$A$ 集合要改变的是一段区间 $[x+2,r]$,他们都 $<a[x]$,它们的 $A$ 集合里会多出 $a[x]$。
同理求 $r$ 只需要线段树二分。判断 $f$ 是否要 $+1$ 只需要看 $a[r+1]$ 是否 $=a[x]$。
对于 $i=x,i=x+1$,注意到这个时候我已经求出了其他 $i$ 的 $f$ 值，所以直接按照最初的 $f[i]=f[(L[i]-1) / (R[i]+1)] + 1$ 转移即可,$L[i],R[i]$ 也可线段树二分求。注意要按照从大到小的顺序 DP

$a[x]>a[x+1]$ ,类似分类讨论，不想写了。

用上面的写法是 $O(n + Qlogn)$ 但是因为不知道怎么写这个线段树二分，所以这边想到了有两种做法:

来自大佬 @RiceFruit 的: 在 $[l,r]$ 中查询第一个满足 $max(a[i],a[i+1],..,a[r]) \le val$ 的位置 $i$,就先把 $[l,r]$ 拆成 $log$ 个区间，然后先从后往前扫一遍判断在哪一个子树内，这样对于一整个子树的求解是好做的。
暴力二分用线段树查询的做法，所以是双 $log$ 的。

一看就方法$2$好写，所以一开始写 $O(Q \times log^2n)$,但是这样要跑 $1.6$s，~~当时看着自己TLE的 $8k$ 代码人都炸了~~。
所以还是写第一种吧。

代码有亿点点长,个人码风问题，但真的感觉写出来也是挺不容易的。
Swap函数那里码风突变是因为不加空格看着太恶心了。

code

#include<bits/stdc++.h>
#define PII pair<int,int>
#define fi first
#define se second 
#define int long long 
using namespace std;
const int N=1e5+5,inf=1e18;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,k,T,a[N];
PII t[N];
int L[N],R[N],f[N];
stack<int> st;
struct node1{
	int l,r,maxn;
};
struct SegmentTree1{
	node1 t[N<<2];
	vector<int> v;  //存区间用 
	void pushup(int p){
		if(t[p<<1].maxn>t[p<<1|1].maxn) t[p].maxn=t[p<<1].maxn;
		else t[p].maxn=t[p<<1|1].maxn;
	}
	void build(int p,int l,int r){
		t[p].l=l,t[p].r=r;
		if(l==r){
			t[p].maxn=a[l];
			return;
		}
		int mid=(l+r)>>1;
		build(p<<1,l,mid);
		build(p<<1|1,mid+1,r);
		pushup(p);
	}
	int ask(int p,int l,int r){
		if(l<=t[p].l&&t[p].r<=r){
			return t[p].maxn;
		}
		int mid=(t[p].l+t[p].r)>>1,maxn=0;
		if(l<=mid) maxn=max(maxn,ask(p<<1,l,r));
		if(r>mid) maxn=max(maxn,ask(p<<1|1,l,r));
		return maxn;
	}
	void Get_range(int p,int l,int r){
		if(l<=t[p].l&&t[p].r<=r){
			v.push_back(p);
			return;
		}
		int mid=(t[p].l+t[p].r)>>1;
		if(l<=mid) Get_range(p<<1,l,r);
		if(r>mid) Get_range(p<<1|1,l,r);
	}
	int lower1(int p,int val,int op){
		if(t[p].l==t[p].r){
			if( (op==0&&t[p].maxn<val) || (op==1&&t[p].maxn<=val) ) return t[p].l;
			else return n+1; 
		}
		if( (op==0&&t[p<<1|1].maxn<val) || (op==1&&t[p<<1|1].maxn<=val) ) return min(lower1(p<<1,val,op) , t[p<<1|1].l);
		else return lower1(p<<1|1,val,op);
	}
	int lower2(int p,int val,int op){
		if(t[p].l==t[p].r){
			if( (op==0&&t[p].maxn<val) || (op==1&&t[p].maxn<=val) ) return t[p].l;
			else return 0; 
		}
		if( (op==0&&t[p<<1].maxn<val) || (op==1&&t[p<<1].maxn<=val) ) return max(t[p<<1].r , lower2(p<<1|1,val,op));
		else return lower2(p<<1,val,op);
	}
	int ask1(int l,int r,int val,int op){  //在 l~r 中查询第一个满足 max(a[i],a[i+1],..,a[r]) </<=  val 的位置 
		if(l>r) return n+1;
		if( (op==0&&a[r]>=val) || (op==1&&a[r]>val) ) return n+1;  //先保证有解 
		v.clear();  //子树下标放这个里面,从左往右放 
		Get_range(1,l,r);
		int ans=r;
		for(int i=v.size()-1;i>=0;i--){
			int p=v[i];
			if( (op==0&&t[p].maxn<val) || (op==1&&t[p].maxn<=val) ) ans=min(ans,t[p].l);  //这里只需要比当前子树的最大值就好了，扫过的那些已经满足了 
			else{
				ans=min(ans,lower1(p,val,op));
				break;
			}
		}
		return ans;
	}
	int ask2(int l,int r,int val,bool op){  //在 l~r 中查询最后一个满足 max(a[l],a[l+1],..,a[i]) </<=  val 的位置 
		if(l>r) return 0;
		if( (op==0&&a[l]>=val) || (op==1&&a[l]>val) ) return 0; 
		v.clear(); 
		Get_range(1,l,r);
		int ans=l;
		for(int i=0;i<v.size();i++){
			int p=v[i];
			if( (op==0&&t[p].maxn<val) || (op==1&&t[p].maxn<=val) ) ans=max(ans,t[p].r); 
			else{
				ans=max(ans,lower2(p,val,op));
				break;
			}
		}
		return ans;	
	}
	void change(int p,int x,int val){
		if(t[p].l==t[p].r){
			t[p].maxn=val;
			return;
		}
		int mid=(t[p].l+t[p].r)>>1;
		if(x<=mid) change(p<<1,x,val);
		else change(p<<1|1,x,val);
		pushup(p);
	}
}Seg1;
struct node2{
	int l,r,sum,add;
	void tag(int d){
		sum+=(r-l+1ll)*d,add+=d;
	}
};
struct SegmentTree2{
	node2 t[N<<2];
	void pushup(int p){
		t[p].sum=t[p<<1].sum+t[p<<1|1].sum;
	}
	void spread(int p){
		if(t[p].add){
			t[p<<1].tag(t[p].add);
			t[p<<1|1].tag(t[p].add);
			t[p].add=0;
		}
	}
	void build(int p,int l,int r){
		t[p].l=l,t[p].r=r;
		if(l==r){
			t[p].sum=f[l];
			return;
		}
		int mid=(l+r)>>1;
		build(p<<1,l,mid);
		build(p<<1|1,mid+1,r);
		pushup(p);
	}
	void change(int p,int x,int val){  
		if(t[p].l==t[p].r){
			t[p].sum=val;
			return;
		}
		spread(p);
		int mid=(t[p].l+t[p].r)>>1;
		if(x<=mid) change(p<<1,x,val);
		else change(p<<1|1,x,val);
		pushup(p);
	}
	void modify(int p,int l,int r,int d){  
		if(l<=t[p].l&&t[p].r<=r){
			t[p].tag(d);
			return;
		}
		spread(p);
		int mid=(t[p].l+t[p].r)>>1;
		if(l<=mid) modify(p<<1,l,r,d);
		if(r>mid) modify(p<<1|1,l,r,d);
		pushup(p);	
	}
	int ask(int p,int l,int r){
		if(l<=t[p].l&&t[p].r<=r){
			return t[p].sum;
		}
		spread(p);
		int mid=(t[p].l+t[p].r)>>1,res=0;
		if(l<=mid) res+=ask(p<<1,l,r);
		if(r>mid) res+=ask(p<<1|1,l,r);
		return res;
	}
	int ask2(int p,int x){
		if(t[p].l==t[p].r) return t[p].sum;
		spread(p);
		int mid=(t[p].l+t[p].r)>>1;
		if(x<=mid) return ask2(p<<1,x);
		else return ask2(p<<1|1,x);
	}
}Seg2;
void Init(){
	st.push(0);
	for(int i=1;i<=n;i++){
		while(st.size()&&a[st.top()]<=a[i]) st.pop();
		L[i]=st.top()+1ll;
		st.push(i);
	}
	while(st.size()) st.pop();
	st.push(n+1);
	for(int i=n;i>=1;i--){
		while(st.size()&&a[st.top()]<=a[i]) st.pop();
		R[i]=st.top()-1ll;
		st.push(i);
	}	
	
	f[0]=f[n+1]=-1ll;
	sort(t+1,t+n+1,[](PII x,PII y){return x.fi>y.fi;});
	for(int i=1;i<=n;i++){
		if(a[L[t[i].se]-1] < a[R[t[i].se]+1]) f[t[i].se]=f[L[t[i].se]-1]+1ll;
		else f[t[i].se]=f[R[t[i].se]+1]+1ll;
	}
	
	Seg1.build(1,0,n+1);
	Seg2.build(1,0,n+1);     //虽然查不到 0/n+1 但是可能要用 
}
void Swap(int x){
	if(a[x]==a[x+1]) return;
	if(a[x]<a[x+1]){
		int l = Seg1.ask1(1 , x-1 , a[x] , 0);
		if(l<=x-1 && a[l-1] != a[x]) Seg2.modify(1 , l , x-1 , -1ll);
		
		int r=Seg1.ask2(x+2 , n , a[x] , 0);
		if(r>=x+2 && a[r+1] != a[x]) Seg2.modify(1 , x+2 , r , 1ll);
		
		Seg1.change(1 , x , a[x+1]) , Seg1.change(1 , x+1 , a[x]);  
		int maxn=a[x+1],ming=a[x]; 
		swap(a[x],a[x+1]);  
		//先更新大的再更新小的 
		int L1 = Seg1.ask1(1 , x , maxn , 1) , R1 = Seg1.ask2(x , n , maxn , 1) , F;  //注意这个时候 a[x+1] 在 x 的位置
		if( a[L1-1] < a[R1+1] ) F = Seg2.ask2(1 , L1-1) + 1ll;
		else F = Seg2.ask2(1 , R1+1) + 1ll;
		Seg2.change(1 , x , F);
		L1 = Seg1.ask1(1 , x+1 , ming , 1) , R1 = Seg1.ask2(x+1 , n , ming , 1) , F;  //注意这个时候 a[x] 在 x+1 的位置
		if( a[L1-1] < a[R1+1] ) F = Seg2.ask2(1 , L1-1) + 1ll;
		else F = Seg2.ask2(1,R1+1) + 1ll;
		Seg2.change(1 , x+1 , F);
		
	}
	else{  //a[x]>a[x+1]
		int l = Seg1.ask1(1 , x-1 , a[x+1] , 0);   //此时可能多出来一个 a[x+1] 
		if(l<=x-1 && a[l-1] != a[x+1]) Seg2.modify(1 , l , x-1 , 1ll);
		
		int r = Seg1.ask2(x+2 , n , a[x+1] , 0);
		if(r>=x+2 && a[r+1] != a[x+1]) Seg2.modify(1 , x+2 , r , -1ll);
		
		Seg1.change(1 , x ,a[x+1]) , Seg1.change(1 , x+1 , a[x]); 
		int maxn=a[x],ming=a[x+1];
		swap(a[x],a[x+1]);  		
		int L1 = Seg1.ask1(1 , x+1 , maxn , 1) , R1 = Seg1.ask2(x+1 , n , maxn , 1) , F;  
		if( a[L1-1] < a[R1+1] ) F = Seg2.ask2(1 , L1-1) + 1ll;
		else F = Seg2.ask2(1 , R1+1) + 1ll;
		Seg2.change(1 , x+1 , F);
		L1 = Seg1.ask1(1 , x , ming , 1) , R1 = Seg1.ask2(x , n , ming , 1) , F; 
		if( a[L1-1] < a[R1+1] ) F = Seg2.ask2(1 , L1-1) + 1ll;
		else F = Seg2.ask2(1 , R1+1) + 1ll;
		Seg2.change(1 , x , F);
		
	}
}
signed main(){
	freopen("summer.in","r",stdin);
	freopen("summer.out","w",stdout);
	n=read(),k=read();
	for(int i=1;i<=n;i++) a[i]=read(),t[i].fi=a[i],t[i].se=i; 
	a[0]=a[n+1]=inf;
	Init();
	T=read();
	while(T--){
		int x=read(),l=read(),r=read();
		Swap(x);
		printf("%lld\n",Seg2.ask(1,l,r)*k + (n-1)*(r-l+1));
	}
	return 0;
}

标签：int,题单,long,times,getchar,&&,动态,规划,mod
From： https://www.cnblogs.com/FloatingLife/p/18396056