题目传送门
题目大意:
给定一个长度为 \(m\) 且只含 \(0\sim 9\) 的字符串 \(s\),求出所有长度为 \(n\) 的,只含 \(0\sim 9\) 且不含 \(s\) 字符串的数量,结果对 \(mod\) 取模。
数据范围:\(n\le 10^9,m\le 20,k\le 1000\)。
思路:
不难发现和 这道题 很像,只是 \(n\) 的数据范围被扩大到了 \(10^9\),\(m\) 的范围被缩小到了 \(20\)。
朴素 dp 思路在 状态机模型 dp 中写了,这里只讲优化。
朴素做法的时间复杂度为 \(O(nm)\),由于这道题的 \(n\) 很大,所以 TLE 无疑了。
观察一下状态转移方程:
\[f(i + 1, \delta(\pi (j), ch)) \leftarrow f(i, j) \]对于每个 \(j\),它有 \(10\) 种状态,分别是字符 \(0\sim 9\),而若 \(j\) 和将要填的字符 \(ch\) 一定,那么 \(\delta(\pi (j), ch)\) 显然也一定,即转移到的地方也相同,而这种转移对于每一个 \(i\) 都要做一次,所以应该优化这个过程。
把状态转移方程展开,以 \(f(i + 1,0\sim m - 1)\) 这一层为例:
\[\left\{\begin{matrix} f(i + 1, 0) = a_{0, 0}\times f(i, 0) + a_{1, 0}\times f(i, 1) + \cdots + a_{m - 1, 0}\times f(i, m - 1) & & \\ f(i + 1, 1) = a_{0, 1}\times f(i, 0) + a_{1, 1}\times f(i, 1) + \cdots + a_{m - 1, 1}\times f(i, m - 1) & & \\ \vdots & & \\ f(i + 1, m - 1) = a_{0, m - 1}\times f(i, 0) + a_{1, m - 1}\times f(i, 1) + \cdots + a_{m - 1, m -1}\times f(i, m - 1) & & \end{matrix}\right. \]这不就是矩阵乘法的形式吗?
根据上面的分析,我们构造的矩阵 \(A\) 与 \(i\) 无关,所以设 \(F(i) = \begin{bmatrix} f(i, 0) & f(i, 1) &\cdots & f(i, m - 1)\end{bmatrix}\),那么 \(F(i + 1) = F(i)\times A\),不难推出 \(F(n) = F(0)\times A^n\),然后就可以用矩阵快速幂算了。
现在的问题变成了如何构造矩阵 \(A\)。
根据状态转移方程,若 \(f(i, j)\rightarrow f(i + 1, p)\),那么说明要得到 \(f(i + 1, p)\) 要加上 \(f(i, j)\),即 \(A\) 矩阵中的第 \(j\) 行 \(p\) 列要加上 \(1\)。
为什么呢,看这张图就明白了:
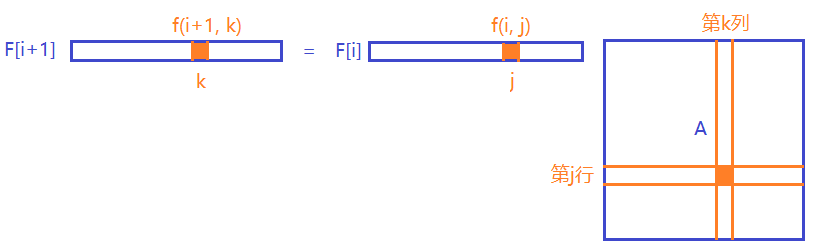
其实图是我偷的(
那么矩阵 \(A\) 就构造好了,这道题也做完了。
流程:
先预处理 KMP 的 \(ne\) 数组,然后预处理出 \(A\) 矩阵,最后直接矩阵快速幂输出答案即可。
时间复杂度:\(O(m^3\cdot \log n)\)。
\(\texttt{Code:}\)
#include <cstring>
#include <iostream>
using namespace std;
const int N = 25;
int n, m, mod;
char s[N];
int ne[N];
struct Matrix {
int mar[N][N];
Matrix() {memset(mar, 0, sizeof mar);}
void init() {
memset(mar, 0, sizeof mar);
for(int i = 0; i < m; i++)
mar[i][i] = 1;
}
Matrix operator *(const Matrix &o) const {
Matrix res;
for(int i = 0; i < m; i++)
for(int j = 0; j < m; j++)
for(int k = 0 ; k < m; k++)
res.mar[i][j] = (res.mar[i][j] + mar[i][k] * o.mar[k][j]) % mod;
return res;
}
}A;
int qpow(int k) {
Matrix res;
res.mar[0][0] = 1;
while(k) {
if(k & 1) res = res * A;
A = A * A;
k >>= 1;
}
int ans = 0;
for(int i = 0; i < m; i++)
ans = (ans + res.mar[0][i]) % mod;
return ans;
}
int main() {
scanf("%d%d%d%s", &n, &m, &mod, s + 1);
for(int i = 2, j = 0; i <= m; i++) {
while(j && s[j + 1] != s[i]) j = ne[j];
if(s[j + 1] == s[i]) j++;
ne[i] = j;
}
for(int j = 0; j < m; j++)
for(int k = '0'; k <= '9'; k++) {
int p = j;
while(p && s[p + 1] != k) p = ne[p];
if(s[p + 1] == k) p++;
if(p < m) A.mar[j][p]++;
}
printf("%d\n", qpow(n));
return 0;
}