蓝月の笔记——莫队篇
简介
莫队算法是由莫涛提出的算法。在莫涛提出莫队算法之前,莫队算法已经在 Codeforces 的高手圈里小范围流传,但是莫涛是第一个对莫队算法进行详细归纳总结的人。莫涛提出莫队算法时,只分析了普通莫队算法,但是经过 OIer 和 ACMer 的集体智慧改造,莫队有了多种扩展版本。
莫队算法可以解决一类离线区间询问问题,适用性极为广泛。同时将其加以扩展,便能轻松处理树上路径询问以及支持修改操作。但是我不会
这段话是抄的
摘要
暴力乱搞做法
Prob.
没有特别说明都是在讲这道题
Part 1 暴力搞法
很显然,可以使用 \(O(n^2)\) 来在线回复询问,开一个 vis[] 将区间扫一遍即可
代码:
// BLuemoon_
#include <bits/stdc++.h>
using namespace std;
const int kMaxN = 1e6 + 5;
int n, m, l, r, ans, a[kMaxN], vis[kMaxN];
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
for (cin >> m; m; m--, ans = 0) {
cin >> l >> r, fill(vis, vis + kMaxN, 0);
for (int i = l; i <= r; i++) {
ans += (vis[i] == 0), vis[i]++;
}
cout << ans << '\n';
}
return 0;
}
Part 2 普通莫队
有聪明的小朋友就要问了,不是你就一个傻逼暴力为什么要把在线标粗啊
我的评价是:感觉不如莫队
用 rzx 也想的出来莫队是一个离线算法,这明显就是一个铺垫啊
我们可以先把所有询问离线下来,进行排序,然后按照一定顺序进行拓展,就可以在 \(O(n\sqrt{n})\) 的时间复杂度内算出结果了
那又有聪明的小朋友要问了,那排序的顺序是什么呢
首先我们明显可以在 \(O(1)\) 将 \([l,r]\) 的询问拓展到相邻的 \([l,r+1],[l,r-1],[l-1,r],[l+1,r]\),那么我们可以以 \(l\) 为第一关键字,\(r\) 为第二关键字惊醒排序,这样就可以做到最优 \(O(n)\) 最坏 \(O(n^2)\) 了
为什么会被卡到 \(O(n^2)\) 呢,我们可以把询问 \([l,r]\) 抽象成平面上的点 \((l,r)\),两个询问之间的拓展次数就是他们的曼哈顿距离,有因为询问保证 \(l \le r\),所以这些点都在 \(y=x\) 之上,于是我们就可以用这样的图形来卡这种做法
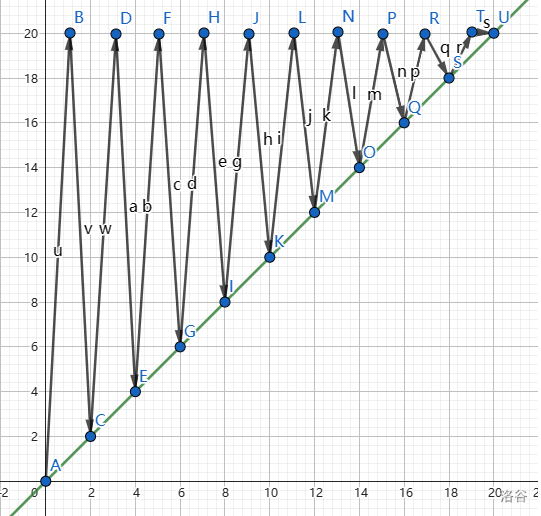
用 rzx 也看的出来这么算是 \(O(n^2)\) 的,那么我们怎么优化呢,当然使用卡常界最泛用的分块啦
我们可以按 \(x\) 坐标分成 \(B\) 块,按点所在块的编号最为第一关键字,\(y\) 坐标作为第二关键字进行排序
这当块长为 \(\sqrt{n}\) 时,可以将时间复杂度降到 \(O(n\sqrt{n})\) ,懒得证明了,自己看去吧

但是我们还可以进行常数优化,因为最坏情况下从前一个块跳到后一个块可能需要 \(O(n)\) 次拓展,所以我们可以对于奇数编号按 \(y\) 坐标从小到大排序,偶数编号从大到小排序,这样就可以稍微平缓的坐过山车了
代码:
// BLuemoon_
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int kMaxN = 1e6 + 5;
int n, m, s, L = 1, R;
LL ans, a[kMaxN], c[kMaxN];
struct Q {
int l, r, id;
LL ans;
const bool operator<(const Q& _) {
int lb = (l - 1) / s + 1, rb = (_.l / s + 1);
if (lb != rb) {
return lb < rb;
}
return (lb & 1 ? r < _.r : r > _.r);
}
const bool operator>(const Q& _) {
return id < _.id;
}
};
Q q[kMaxN];
void Insert(int x) {
c[a[x]]++, ans += (c[a[x]] == 1);
}
void Delete(int x) {
c[a[x]]--, ans -= (c[a[x]] == 0);
}
bool CMP(Q l, Q r) {
return l.id < r.id;
}
int main() {
cin >> n, s = sqrt(n);
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
cin >> m;
for (int i = 1; i <= m; i++) {
cin >> q[i].l >> q[i].r, q[i].id = i;
}
sort(q + 1, q + m + 1);
for (int i = 1; i <= m; i++) {
for (; R < q[i].r; Insert(++R)) {
}
for (; L > q[i].l; Insert(--L)) {
}
for (; R > q[i].r; Delete(R--)) {
}
for (; L < q[i].l; Delete(L++)) {
}
q[i].ans = ans;
}
sort(q + 1, q + m + 1, CMP);
for (int i = 1; i <= m; i++) {
cout << q[i].ans << '\n';
}
return 0;
}
你说的对,但是这份代码只有 \(36\) 分,因为 \(O(n\sqrt{n})\) 可能达到 \(10^9\),能过才怪,但是如果你卡卡常或许可以达到 \(50\sim 70\) 分,我在最多卡到了 \(52\),加油吧