定义
字符串
对于一个字符串 \(S\),\(S\) 由 \(n\) 个字符组成,其中 \(n\) 是 \(S\) 的长度,表示为 \(|S|\)。
子串
从一个字符串 \(S\) 中取出连续的一段 \(T\),则 \(T\) 为 \(S\) 的子串。
子序列
从一个字符串 \(S\) 中顺序取出一些字符,组成的新的字符串就是 \(S\) 的子序列。
前缀
从 \(S\) 的第一个字符开始取的子串。
后缀
以 \(S\) 的最后一个字符结束的子串。
回文串
正着和倒着都一样的字符串。
周期
我们定义,如果一个字符串是以一个或者一个以上的长度为 \(k\) 的重复字符串所连接成的,那么这个字符串就叫做周期为 \(k\) 的串。
\(\text C++\) 标准库
s.c_str()/s.data()返回一个指针,内容就是原来的字符串。s.size()返回字符个数。s.find(c, begin)查找并返回从begin开始的c的位置。s.substr(begin,len)从begin开始截取一段长度为len的字符。s.append(s',pos,len)将s'中从pos开始的len个字符接到s的末尾。s.replace(pos,n,s')将s中从pos开始的长为n的子串替换成s'。s.erase(pos,len)删除从pos开始的len个字符。s.insert(pos,s')在pos处插入s'。
哈希
定义
哈希其实就是一个映射,它通过一个函数将一些抽象的东西变成直观的数字,方便我们去比较信息。
字符串哈希
就是把字符串通过映射变成一个数,方便比较。一般把字符串看成一个多位数,进制取一个质数,然后选择一个大模数。
性质
- 哈希值不同的原来一定不同。
- 哈希值相同的原来不一定相同。
如果原来不同但是哈希值相同,我们称此为哈希冲突。
哈希冲突
我们设哈希后字符串取值范围为 \(mod\),字符串数量为 \(n\),则哈希冲突概率为:
\[p(n,mod)=1-\exp(-\frac{n(n-1)}{2mod}) \]证明:
先算哈希不冲突的概率为:
\[\overline{p}(n,mod)=1\times(1-\frac{1}{mod})\times(1-\frac{2}{mod})\times\dots\times(1-\frac{n-1}{mod}) \]然后根据泰勒公式:
\[\exp(x)=\sum_{i=0}^{\infty}\frac{x^i}{i!}=1+x+\frac{x^2}{2}+\frac{x^3}{6}+\dots \]当 \(x\) 非常小时,\(\exp(x)\) 趋近于 \(x+1\)。
所以之前的式子就可以写成:
\[\begin{array} \overline{p}(n,mod)&=1\times\exp(-\frac{1}{mod})\times\exp(-\frac{2}{mod})\dots\times\exp(-\frac{n-1}{mod})\\ &=\exp(-\frac{1}{mod}-\frac{2}{mod}-\dots-\frac{n-1}{mod})\\ &=\exp(-\frac{n(n-1)}{2mod}) \end{array} \]所以哈希冲突概率为:
\[p(n,mod)=1-\exp(-\frac{n(n-1)}{2mod}) \]那么,我们在实际写题的时候又应该如何避免呢?
双哈希
顾名思义,就是对于一个字符串分别设置两个函数,判断是否相等就看两个哈希值是否都相等即可。
例题
P3370 【模板】字符串哈希
板子题没啥好说的。
P2757 [国家集训队] 等差子序列 Problem - 452F - Codeforces 双倍经验
题解
转化题意,就是在序列中找到一个位置 \(i\),对于 \(a_i\) 找到一个 \(t\) 使得 \(a_i-t\) 和 \(a_i+t\) 分别在 \(a_i\) 的两侧。首先可以想到去枚举中间数,暴力去找。
如何优化呢?假设现在有一个数组 \(b\)。当我们枚举中间数,左侧的全部标记为1。对于枚举的数 \(x\),我们需要去判断每一个可能的 \(t\) 是否有 \(x-t\) 和 \(x+t\) 在数组 \(b\) 的值是否相等。这就像在序列中抓出一段子串去判断是否为回文串,然后还要支持单点修改。
到这里我们就用线段树做就行了。维护正序倒序两种哈希值,单点修改就做完了。
(由于没写所以代码就不放啦喵)
P3449 [POI2006] PAL-Palindromes
题解
先去寻找题目性质。首先能发现输入的都是回文串!然后想一想如果两个串要组成大的回文串需要什么条件?
我们先假设有两个回文串 \(s\) 和 \(t\),我们假设 \(s\) 的最小周期是 \(c\),那么 \(s\) 可以表示成 \(c^p\)。如果 \(s\) 和 \(t\) 能够拼成回文串,那么 \(t\) 一定也能写成 \(c^q\) 的形式。所以当两个回文串的最小周期相同的时候就能够拼成回文串。
我们就开一个 map 记一下每个最小周期相同的个数然后就做完了。时间复杂度小于调和级数所以是 \(\Theta(n\log n)\)。
代码
int n, m;
const int b1 = 133, b2 = 233, m1 = 1e9 + 7, m2 = 1e9 + 9;
ll h1[N], h2[N], s1[N], s2[N], ans;
char s[N];
map < pll , ll > mp;
pll aim;
pll geth(int l, int r){
ll x1 = (h1[r] - h1[l - 1] * s1[r - l + 1] % m1) + m1; x1 %= m1;
ll x2 = (h2[r] - h2[l - 1] * s2[r - l + 1] % m2) + m2; x2 %= m2;
return mkp(x1, x2);
}
bool eq(pll x, pll y){
return x.first == y.first and x.second == y.second;
}
bool chk(int len){
for(int i = len + 1; i <= m; i += len)if(! eq(geth(i, i + len - 1), aim))return false;
return true;
}
signed main(){
n = rd(); s1[0] = s2[0] = 1;
for(int i = 1; i < N; ++i)s1[i] = s1[i - 1] * b1 % m1, s2[i] = s2[i - 1] * b2 % m2;
while(n--){
m = rd(); scanf("%s", s + 1);
for(int i = 1; i <= m; ++i)h1[i] = (h1[i - 1] * b1 % m1 + s[i]) % m1, h2[i] = (h2[i - 1] * b2 % m2 + s[i]) % m2;
for(int i = 1; i <= m; ++i)if(m % i == 0){
aim = geth(1, i);
if(chk(i)){ans += (mp[aim]++ << 1) + 1; break;}
}
}
printf("%lld", ans);
return 0;
}
KMP
介绍
KMP 算法是解决字符串中的匹配问题的高效算法。最基本的问题是给你一个文本串和模式串,让你求出模式串在匹配串中出现的位置、次数等。
匹配问题
关于这个问题其实有很多的做法。
- 暴力做法:枚举文本串每个位置作为起点开始按位匹配,如果不行就换起点。
- 哈希做法:预处理出文本串与模式串的哈希值然后 \(O(|S|)\) 比较。
- KMP!
前言
虽然就一个模式串和一个匹配串的题看不出哈希和 KMP 的差距,但 KMP 的思想可以用于解决多模式串匹配串的题,这也就是学习 KMP 的意义。
字符串的 border
前言
border 是一个非常重要的概念,所以在介绍所有匹配的东西之前我们需要先了解 border 以及它的一些性质。
概念
如果字符串的一个真前缀和真后缀相等,那么我们称此为这个字符串的 border。
性质
周期有关
- 如果一个前缀 \(s[1\dots i]\) 是 \(s\) 的 border,那么 \(|s|-i\) 是 \(s\) 的周期。
- 若 \(p,q\) 都是 \(s\) 的周期,且 \(p+q≤|s|\),则 \(\gcd(p,q)\) 也是 \(s\) 的周期。
性质 1 很简单可以画图自证;
性质 2 证明:钦定 \(p<q\),设 \(d=q-p,n=|s|\)。
- 对于 \(i\in[p+1,n]\),我们能发现 \(s[i]=s[i-p]=s[i-p+q]=s[i+d]\);
- 对于 \(i\in[1,n-q]\),我们同样能发现 \(s[i]=s[i+q]=s[i+q-p]=s[i+d]\)。
\(\because p+q\le n,\therefore p\le n-q\),因此上述两种情况能够涵盖整个字符串,所以 \(d\) 也是 \(s\) 的一个周期,然后令 \(q=p,p=d\) 重复上面的过程(类似辗转相除法)就可以得到性质 2。
border 本身性质
- 对于一个字符串 \(s\),它的所有长度 \(\ge\frac{|s|}{2}\) 的 border 的长度是等差序列。
- 字符串的所有 border 组成 \(O(\log n)\) 个等差序列。
性质 3 证明:假设我们知道最大的 border 是 d,那么字符串的最小周期为 \(r=|s|-d\)。因为 \(r\) 是最小的周期,那么 \(2r,3r,4r\dots\) 也就一定是周期,所以这些周期对应的 border \(d-r,d-2r,d-3r\dots\) 也就为等差序列。
性质 4 证明:首先对于长度 \(\ge\frac{|s|}{2}\) 的 border 我们可以性质 3 处理,这里只讨论其余的 border。假设现在剩下的 border 中最长的为 \(B\)(如图),而对于其他任意的 border \(A\),都有 \(A\) 是 \(B\) 的 border。至于原因可以根据定义推一推,下图已经画得很不清晰了。
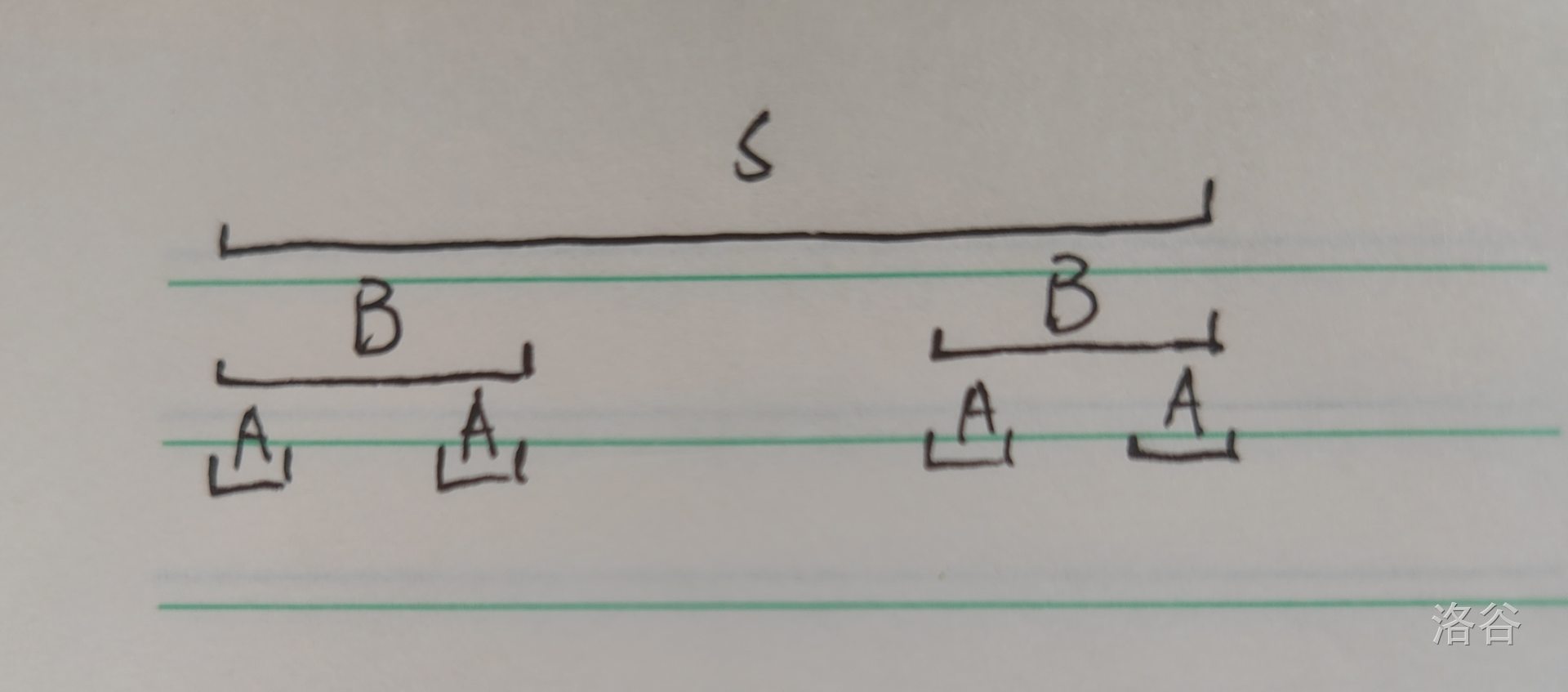
所以又可以根据性质 3 又分出一些长度 \(\ge\frac{|B|}{2}\) 的 border,然后以此类推。因为每次 \(|B|\) 都至少减半,所以是 \(\log n\) 的。
例题:WC2016 论战捆竹竿
题解
考虑一个串不同的贡献就是这个串的长度减去 border,然后可以将题意转化为给你一些数,问你可以凑出多少不超过 \(w-n\) 的数。如果凑出 \(\bmod n\) 余 \(0\dots n\) 的数,那么每次加 \(n\) 就可以凑出新的数,所以可以想到同余最短路。如果直接暴力连边就是 \(O(n^2)\) 的复杂度,所以考虑优化。
因为 border 的性质是 \(O(\log n)\) 的等差序列,我们可以分开考虑每一个等差序列,然后在转移两个不同的等差序列。对于一个等差序列 \(A_i=x+d\times i\),他们在 \(\bmod x\) 的意义下可以分成 \(\gcd(x,d)\) 个环,读者可自行画图证明。对于每一个点 \(i\) 向 \((i+d)\%x\) 连边,然后就有了转移方程:
\[f_i=\min(f_j+x+(id_i-id_j)\times d) \]转移时可以单调队列维护 \(f_j-id_j\times d\),我们就选出环上最小的 \(f_i\) 以它为起点转移。
最后考虑两个等差序列之间如何转换。对于一个点 \(i\),我一定是从前面一个数加上了若干倍的 \(x'\) 后在 \(\bmod x\) 的意义下为 \(i\)。然后就可以转化成 \(i\) 向 \((i+x')\%x\) 连边,转移就与上面的式子基本一模一样(就只是少了一个 \(x\))。
因为作者太菜了写不来所以就不放半成品了
前缀函数
在正式讲 KMP 前,我们需要学习前缀函数。
对于一个位置 \(i\),\(\pi(i)\) 表示 \(i\) 的前缀函数,而前缀函数记录的则是子串 \(s[1\dots i]\) 中最长且相等的真前缀与真后缀的长度,换句话说,前缀函数就是最大的 border。
举一个例子:若我现在有一个字符串 \(s=aabaaba\),则每一个位置对应的前缀函数 \(\pi\) 为:0,1,0,1,2,3,1。
如何去求前缀函数?
对于一个字符串,假设我们已经求出 \(\pi(1\dots i-1)\),那应该如何求出 \(\pi(i)\) 呢?
我们知道前缀函数是算的最长相等真前缀真后缀,所以我们可以先去比较 \(s[i]\) 与 \(s[\pi(i-1)+1]\) 的位置。因为 \(s[1\dots\pi(i-1)]=s[i-\pi(i-1)\dots i-1]\),如果它们的下一位相等,那么就可以直接更新 \(\pi(i)\)。
那如果它们不同呢?我们可以记录一个 \(j\),初始为 \(i-1\)。当上述情况不满足条件时,我们令 \(j=\pi[j]\),继续比较 \(s[1\dots\pi(j)]=s[i-\pi(j)\dots i-1]\)。
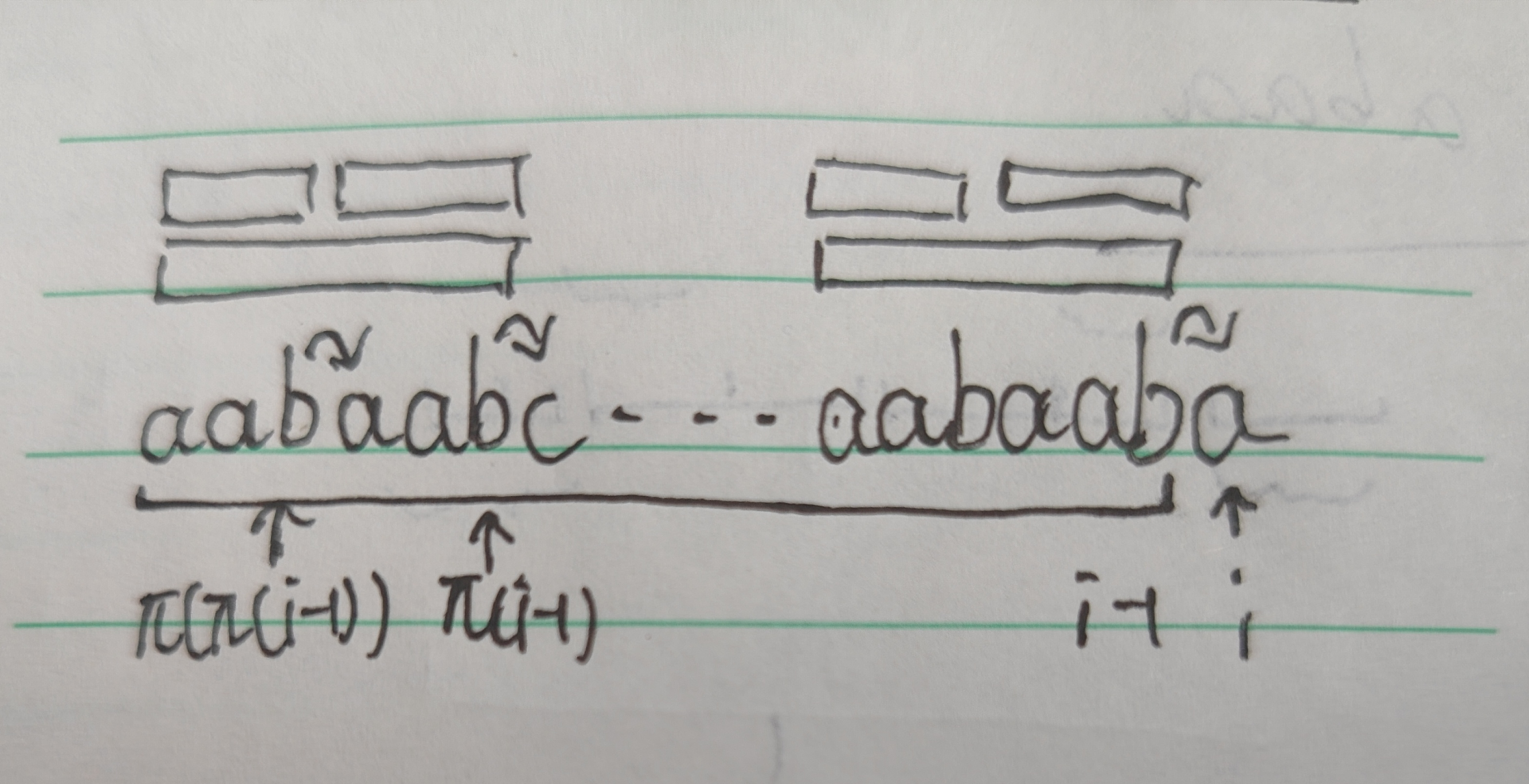
具体的可以参考上面我画的图(好丑)。如果两个大的部分( \(s[1\dots\pi(i-1)],s[i-\pi(i-1)\dots i-1]\))相等,就只用比较下一位;如果发现不等(如图中字符 \(c\) 与 \(a\) 不等),那么就继续回跳前缀函数。然后容易看出图中四个小长方形对应位置的子串相等,如果 \(s[1\dots\pi(j)]=s[i-\pi(j)\dots i-1]\) 那么我们就找到了 \(\pi(i)\)。
我们已经求出前缀函数,那么如何用前缀函数求解匹配问题呢?
KMP 算法
先放图qwq。

看完图我们能发现:这个流程与前面求前缀函数的过程非常类似。我们可以先求出模式串 \(t\) 的前缀函数,然后用类似求前缀函数的方法在匹配串 \(s\) 上扫一遍,如果对于当前的字符 \(s_i\) 与 \(t_{j+1}\) 不匹配,那么就从 \(j+1\) 往回跳。当指针 \(j\) 等于 \(|t|\) 时说明找到了 \(s\) 中一段子串能够匹配 \(t\)。
代码(我远古时期写的板子)
int n, m, j, k[N];
char a[N], b[N];
void solve(){
cin >> a + 1;
cin >> b + 1;
n = strlen(a + 1); m = strlen(b + 1);
FL(i, 2, m){
while(j and b[i] != b[j + 1])j = k[j];
if(b[i] == b[j + 1])j++;
k[i] = j;
}
j = 0;
FL(i, 1, n){
while(j > 0 and a[i] != b[j + 1])j = k[j];
if(a[i] == b[j + 1])j++;
if(j == m){
cout << i - m + 1 << '\n';
j = k[j];
}
}
FL(i, 1, m)cout << k[i] << ' ';
}
例题
USACO15FEB Censoring S
题解:
疑似板子?就是在匹配文本串时用栈代替数组,当找到一个匹配时就把这一段弹出去,然后维护一下前缀函数即可。
代码
int n, m, fail[N], j, top, cur[N];
char a[N], b[N], st[N];
signed main(){
// fileio(fil);
scanf("%s %s", a + 1, b + 1); n = strlen(a + 1), m = strlen(b + 1);
for(int i = 2; i <= m; ++i){
while(j and b[i] ^ b[j + 1])j = fail[j];
if(b[i] == b[j + 1])++j; fail[i] = j;
}
j = 0;
for(int i = 1; i <= n; ++i){
st[++top] = a[i];
while(j and st[top] ^ b[j + 1])j = fail[j];
if(st[top] == b[j + 1])++j;
if(j == m)top -= m, j = cur[top];
cur[top] = j;
}
for(int i = 1; i <= top; ++i)putchar(st[i]);
return 0;
}
P4391 BOI2009 Radio Transmission 无线传输
题解
找周期就直接用长度减去 \(\pi(|S|)\) 即可。
trie 树
介绍
顾名思义就是一颗朴实无华的树。有一个根,从根往下有一些子树,从根到某个点的路径就是一个字符串。

这里引用了 OI-wiki 上的一张图,以便读者能更直观地理解 trie 树。比如 12 号点就代表了一个字符串 \(\text caa\)。
这里先给出 trie 的板子。
int T, n, m;
char s[N];
map < char, int > mp;
struct trie{
int cnt, nex[N][63], ext[N];
void ins(char *s, int l){
int p = 0;
FL(i, 1, l){
int ch = mp[s[i]];
if(! nex[p][ch])nex[p][ch] = ++cnt;
p = nex[p][ch]; ext[p]++;
}
}
int query(char *s, int l){
int p = 0;
FL(i, 1, l){
int ch = mp[s[i]];
if(! nex[p][ch])return 0;
p = nex[p][ch];
}
return ext[p];
}
void clear(){
FL(i, 0, cnt){
ext[i] = 0;
FL(j, 0, 62)nex[i][j] = 0;
}cnt = 0;
}
}t;
void init(){
int tot = 0;
for(char i = 'a'; i <= 'z'; i++)mp[i] = ++tot;
for(char i = 'A'; i <= 'Z'; i++)mp[i] = ++tot;
for(char i = '0'; i <= '9'; i++)mp[i] = ++tot;
}
那么 trie 树又有什么用呢?
应用
- 查询字符串。直接沿着树边走就行,如果走到空节点就说明不存在这个字符串。
- 与 KMP 合体变成 ACAM!这个会在其他博客中讲。
- 01 trie
这里稍微讲一下 01 trie。
01 trie
01 trie 是一种特殊的 trie,它维护了一些由 0 和 1 组成的字符串。然后对于任意整数我们都可以把它写成二进制,这样我们就能够用 01 trie 维护一些数了,而且把这些数丢进 01 trie 中它会自动排好序,然后你也许会意识到它(01 trie)就类似一颗平衡树。然而作者数据结构学得西撇,所以不在此讲有关维护 01 trie 的内容,对于字符串只要知道 trie 能够查询字符串也许就行了。(逃
例题
P2580 于是他错误的点名开始了
题解
就是普通的在 trie 上做插入操作,然后每次查询后维护一下字符串是否被第一次询问即可。
P4551 最长异或路径
题解
首先要知道 \(\oplus\) 的性质。比如一些东西异或偶数次就会抵消。然后问题是找树上一条异或和最大的路,我们可以先求出从根节点到每个点的异或和 \(d_i\),然后对于任意两点 \(u,v\) 的路径异或和就能表示为 \(d_u\oplus d_v\)。我们就可以把所有 \(d_i\) 扔进一颗 01 trie 里,然后枚举每一个点,贪心去找最大异或。因为高位更大数值一定更大所以贪心是正确的,然后就做完了。
代码
int n, hd[N], cnt, dis[N], trie[N << 4][2], cnt_t = 1, ans;
bool ed[N << 4];
struct edge{int nxt, to, d;}e[N << 1];
void add(int x, int y, int z){e[++cnt] = (edge){hd[x], y, z}; hd[x] = cnt;}
void dfs(int u, int fa)
{
for(int i = hd[u]; i; i = e[i].nxt)
{
int v = e[i].to, val = e[i].d;
if(v == fa)continue;
dis[v] = dis[u] xor val; dfs(v, u);
}
}
void ins(int x)
{
int k = 1;
for(int i = 31; i > ~ i; i--)
{
int ret = (x >> i) & 1;
if(!trie[k][ret])trie[k][ret] = ++cnt_t;
k = trie[k][ret];
}
ed[k] = true;
}
int find(int x)
{
int k = 1, ans = 0;
for(int i = 31; i > ~ i; i--)
{
int ret = (x >> i) & 1;
if(trie[k][ret xor 1])k = trie[k][ret xor 1], ans += 1 << i;
else k = trie[k][ret];
}
return ans;
}
signed main()
{
cin >> n;
for(int i = 1, x, y, z; i < n; i++)
{
scanf("%d %d %d", &x, &y, &z);
add(x, y, z); add(y, x, z);
}
dfs(1, 0);
for(int i = 1; i <= n; i++)ins(dis[i]);
for(int i = 1; i <= n; i++)ans = max(ans, find(dis[i]));
cout << ans; return 0;
}
最后
以上就是这篇博客的全部内容了,这篇博客以讲基础为主(hash、KMP、trie),加了一点稍难的题目。后面还会写三篇字符串的博客然后结束字符串所有内容,请敬请期待。
参考资料
【算法图文动画详解系列】KMP 字串匹配搜索算法-腾讯云开发者社区-腾讯云
Border / 回文 Border 理论小记 - Lgx_Q - 博客园
标签:frac,int,基础知识,trie,哈希,字符串,border From: https://www.cnblogs.com/Nekopedia/p/18383964