思想
我先给出一些定义:
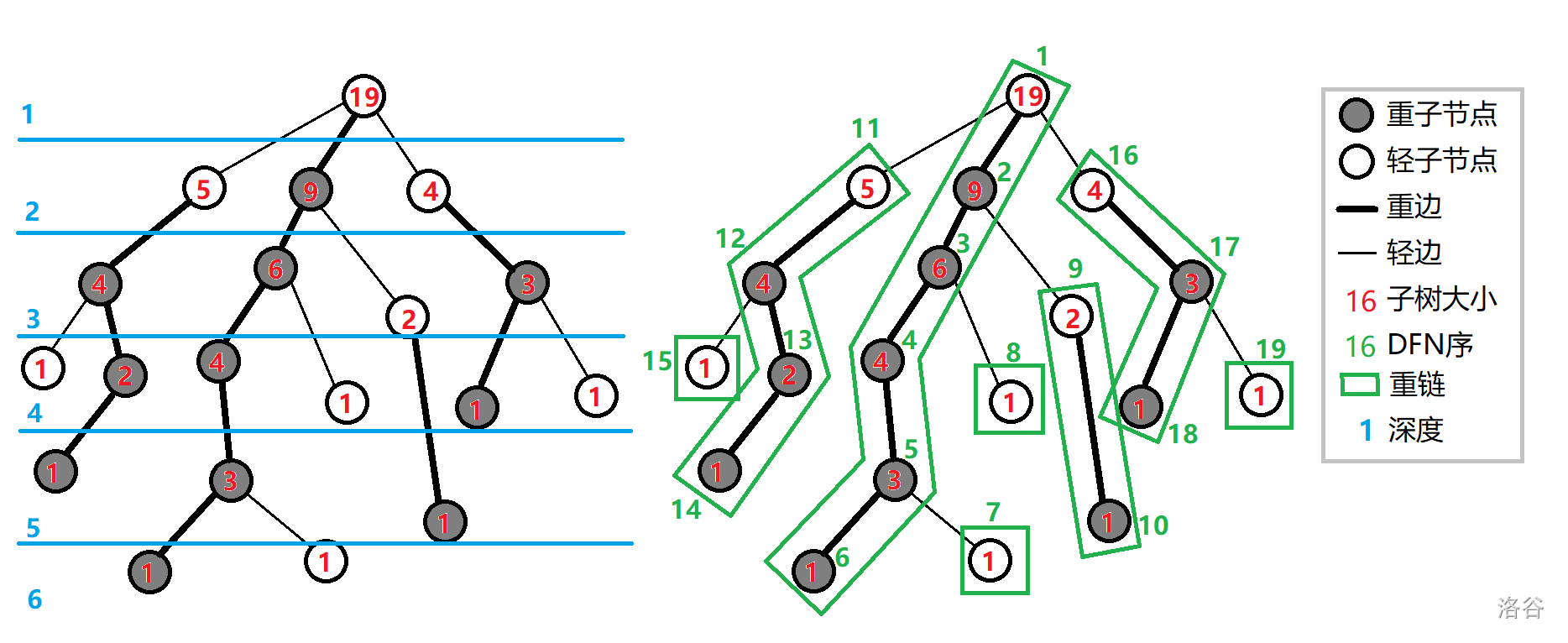
定义一个结点的重子节点为其子节点中子树节点数最大的子节点,如有多个,随便取一个作为重儿子,如果没有子节点,就没有重儿子。
定义一个结点的轻子节点为其除重子节点外的子节点。
从这个节点到重子节点的边为重边,到其他子节点的边为轻边。
由重边首位相连的链称为重链。
把落单的结点也当作重链,那么整棵树就被剖分成若干条重链,可以证明,树上每条路径最多会被分成 \(O(\log{n})\) 条重链。
如图:
预处理
树剖的预处理分为两步。
我们先给出一些定义:
- \(fa(u)\) 表示节点 \(u\) 的父节点
- \(dep(u)\) 表示节点 \(u\) 的深度
- \(siz(u)\) 表示节点 \(u\) 的子树结点个数
- \(son(u)\) 表示节点 \(u\) 的重儿子
- \(top(u)\) 表示节点 \(u\) 所在 重链 的顶部节点(深度最小)
- \(dfn(u)\) 表示节点 \(u\) 的 \(dfs\) 序,也是其在线段树中的编号
- \(rnk(x)\) 表示 \(dfs\) 序所对应的节点编号,有 \(rnk(dfn(u))=u\)
我们进行两遍 \(dfs\) 预处理这些值,第一遍预处理出 \(fa\),\(son\),\(siz\),\(dep\) ,第二遍预处理出 \(top\),\(dfn\),\(rnk\)。
void dfs1(int u){
son[u]=-1;
siz[u]=1;
for(int i=head[u];i;i=g[i].nxt){
int v=g[i].to;
if(!dep[v]){
dep[v]=dep[u]+1;
fa[v]=u;
dfs1(v);
siz[u]+=siz[v];
if(son[u]==-1||siz[v]>siz[son[u]]){
son[u]=v;
}
}
}
return;
}
int cnt=0;
void dfs2(int u,int t){
top[u]=t;
cnt++;
dfn[u]=cnt;
rnk[cnt]=u;
if(son[u]==-1)return;
dfs2(son[u],t);//先访问重儿子使重链上的点dfn序连续
for(int i=head[u];i;i=g[i].nxt){
int v=g[i].to;
if(v!=son[u]&&v!=fa[u]){
dfs2(v,v);
}
}
return;
}
LCA
题面
如题,给定一棵有根多叉树,请求出指定两个点直接最近的公共祖先。
思路
这题做法很多,什么倍增,\(RMQ\),\(tarjan\) 之类的。今天我们来讲用重链剖分做。其实很简单,我们只需要让两个节点不断按一条一条重链跳直到两点处于一条重链时取深度低的即可。
代码
#include<iostream>
#include<cstdio>
using namespace std;
struct edge{
int to;
int nxt;
}g[1000100];
int head[500100],tot;
void addedge(int x,int y){
tot++;
g[tot].to=y;
g[tot].nxt=head[x];
head[x]=tot;
return;
}
int son[500010],top[500010],fa[500010],siz[500010],dep[500010],dfn[500010],rnk[500010];
void dfs1(int u){
son[u]=-1;
siz[u]=1;
for(int i=head[u];i;i=g[i].nxt){
int v=g[i].to;
if(!dep[v]){
dep[v]=dep[u]+1;
fa[v]=u;
dfs1(v);
siz[u]+=siz[v];
if(son[u]==-1||siz[v]>siz[son[u]]){
son[u]=v;
}
}
}
return;
}
int cnt=0;
void dfs2(int u,int t){
top[u]=t;
cnt++;
dfn[u]=cnt;
rnk[cnt]=u;
if(son[u]==-1)return;
dfs2(son[u],t);
for(int i=head[u];i;i=g[i].nxt){
int v=g[i].to;
if(v!=son[u]&&v!=fa[u]){
dfs2(v,v);
}
}
return;
}
inline int lca(int u,int v){
while(top[u]!=top[v]){
if(dep[top[u]]>dep[top[v]]){
u=fa[top[u]];
}else{
v=fa[top[v]];
}
}
return dep[u]>dep[v]?v:u;
}
int main(){
cin.tie(0);
ios::sync_with_stdio(false);
int n,m,s;
cin>>n>>m>>s;
for(int i=1;i<n;++i){
int x,y;
cin>>x>>y;
addedge(x,y);
addedge(y,x);
}
dep[s]=1;
dfs1(s);
dfs2(s,s);
for(int i=1;i<=m;i++){
int x,y;
cin>>x>>y;
cout<<lca(x,y)<<"\n";
}
cout<<flush;
return 0;
}
【模板】重链剖分/树链剖分
题面
如题,已知一棵包含 \(N\) 个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
-
1 x y z,表示将树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值都加上 \(z\)。 -
2 x y,表示求树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值之和。 -
3 x z,表示将以 \(x\) 为根节点的子树内所有节点值都加上 \(z\)。 -
4 x表示求以 \(x\) 为根节点的子树内所有节点值之和
思路
我们先说路径的修改查询,其实很简单,我们可以像跑 \(LCA\) 一样遍历 \(x\) 到 \(y\) 的路径上的每条重链,由于前面我们预处理时已经保证了一条重链的 \(dfn\) 序连续,我们可以将每个点用其 \(dfn\) 序表示,再维护一个 \(nw\) 数组用来存对应 \(dfn\) 序的初始值,用线段树进行区间修改,区间查询即可。再说子树修改查询,这个更简单,由于子树 \(dfn\) 序连续,直接用线段树修改查询即可。
代码
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
struct edge{
int to;
int nxt;
}g[1000100];
int head[500100],tot;
int n,m,r,p;
inline void addedge(int x,int y){
tot++;
g[tot].to=y;
g[tot].nxt=head[x];
head[x]=tot;
return;
}
ll a[100010];
int son[100010],top[100010],fa[100010],siz[100010],dep[100010],dfn[100010];
ll nw[100010];
void dfs1(int u){
son[u]=-1;
siz[u]=1;
for(int i=head[u];i;i=g[i].nxt){
int v=g[i].to;
if(!dep[v]){
dep[v]=dep[u]+1;
fa[v]=u;
dfs1(v);
siz[u]+=siz[v];
if(son[u]==-1||siz[v]>siz[son[u]]){
son[u]=v;
}
}
}
return;
}
int cnt=0;
void dfs2(int u,int t){
top[u]=t;
cnt++;
dfn[u]=cnt;
nw[cnt]=a[u];
if(son[u]==-1)return;
dfs2(son[u],t);
for(int i=head[u];i;i=g[i].nxt){
int v=g[i].to;
if(v!=son[u]&&v!=fa[u]){
dfs2(v,v);
}
}
return;
}
struct node{
ll tag;
ll val;
ll l;
ll r;
}tree[400100];
inline void maketag(int u,ll k){
tree[u].val+=k*(tree[u].r-tree[u].l+1)%p;
tree[u].val%=p;
tree[u].tag+=k;
return;
}
inline void pushup(int u){
tree[u].val=(tree[u<<1].val+tree[u<<1|1].val)%p;
return;
}
inline void pushdown(int u){
maketag(u<<1,tree[u].tag);
maketag(u<<1|1,tree[u].tag);
tree[u].tag=0;
return;
}
void build(int u,int l,int r){
tree[u].l=l;
tree[u].r=r;
tree[u].tag=0;
if(l==r){
tree[u].val=nw[l]%p;
return;
}
int mid=(l+r)>>1;
build(u<<1,l,mid);
build(u<<1|1,mid+1,r);
pushup(u);
return;
}
void modify(int u,int l,int r,ll k){
if(l<=tree[u].l&&tree[u].r<=r){
maketag(u,k);
return;
}
pushdown(u);
int mid=(tree[u].l+tree[u].r)>>1;
if(l<=mid){
modify(u<<1,l,r,k);
}
if(mid<r){
modify(u<<1|1,l,r,k);
}
pushup(u);
return;
}
ll query(int u,int l,int r){
if(l<=tree[u].l&&tree[u].r<=r){
return tree[u].val;
}
pushdown(u);
ll ans=0;
int mid=(tree[u].l+tree[u].r)>>1;
if(l<=mid){
ans+=query(u<<1,l,r);
}
if(mid<r){
ans+=query(u<<1|1,l,r);
}
return ans%p;
}
void mdfpath(int u,int v,ll k){
k%=p;
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]])swap(u,v);
modify(1,dfn[top[u]],dfn[u],k);
u=fa[top[u]];
}
if(dep[u]>dep[v]){
swap(u,v);
}
modify(1,dfn[u],dfn[v],k);
return;
}
ll qrypath(int u,int v){
ll ans=0;
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]])swap(u,v);
ans+=query(1,dfn[top[u]],dfn[u]);
ans%=p;
u=fa[top[u]];
}
if(dep[u]>dep[v])swap(u,v);
ans+=query(1,dfn[u],dfn[v]);
ans%=p;
return ans;
}
void mdftree(int u,int k){
modify(1,dfn[u],dfn[u]+siz[u]-1,k%p);
return;
}
ll qrytree(int u){
return query(1,dfn[u],dfn[u]+siz[u]-1);
}
int main(){
cin.tie(0);
ios::sync_with_stdio(false);
cin>>n>>m>>r>>p;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<n;i++){
int x,y;
cin>>x>>y;
addedge(x,y);
addedge(y,x);
}
dep[r]=1;
dfs1(r);
dfs2(r,r);
build(1,1,n);
while(m--){
int op,x,y,z;
cin>>op>>x;
if(op==1){
cin>>y>>z;
mdfpath(x,y,z%p);
}
if(op==2){
cin>>y;
cout<<qrypath(x,y)<<"\n";
}
if(op==3){
cin>>z;
mdftree(x,z%p);
}
if(op==4){
cout<<qrytree(x)<<"\n";
}
}
cout<<flush;
return 0;
}