前置
单调队列(没学过或忘了点这里)
简化题意
有一块牛排,要求对它烹饪 \(2n\) 秒,可在给定的 \(k\) 个时间段中将它翻转任意次,使得牛排两面都受到了 \(n\) 秒的烹饪。
状态设计
-
可以发现当总共煮了 \(i\) 秒,其中一面如果煮了 \(j\) 秒,自然可以求出另一面为 \(i-j\) 秒,所以我们可以设状态为 前 \(i\) 秒没在烤的面煮了 \(j\) 秒的最小翻转次数,但由于时间 \(n\) 最大为 \(10^5\) ,所以这个状态必然是 开不下 的。
-
不过,可以发现题目要求必须在 给定的 \(k\) 个区间内才能翻转 ,所以可以以每个区间作为一个状态。设 \(dp_{i,j}\) 表示第 \(i\) 个区间结束时,没烤的面煮了 \(j\) 秒的最小翻转次数。最终答案为 \(dp_{k,n}\) 。
转移
考虑有哪些情况会构成转移:
-
一种情况是不翻转,这时没煮的面煮的 时间没有增加 ,所以直接继承上一个区间的状态。
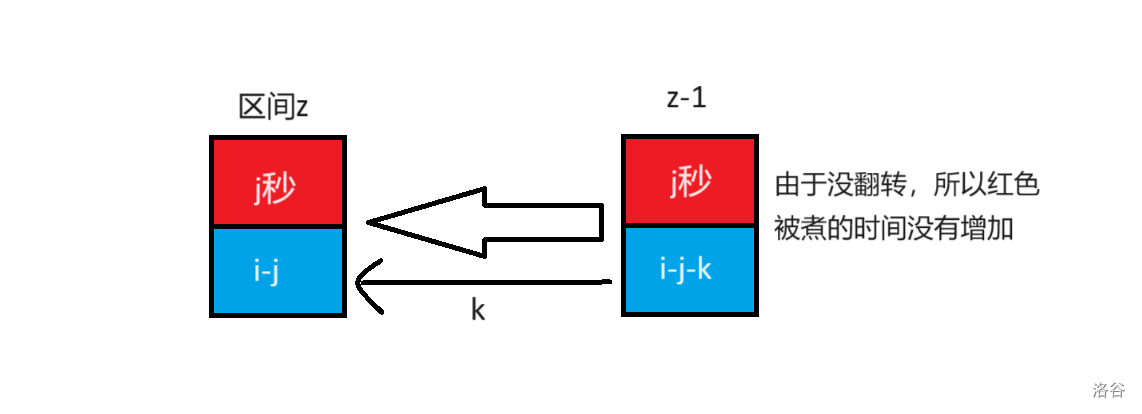
则转移方程为 \(dp_{z,j}=dp_{z-1,j}\) 。
-
考虑在一个区间内翻转多次(钦定每次翻转都在 \(z-1\) 区间结束后):
-
如图所示,翻转很多次可以转换为翻转 一次 或翻转 两次 的情况。(附:每个区间 \(z-1\) 到下一个区间 \(z\) 都看作在区间 \(z-1\) 结束时 立刻翻转 )
- 翻转 一次 :
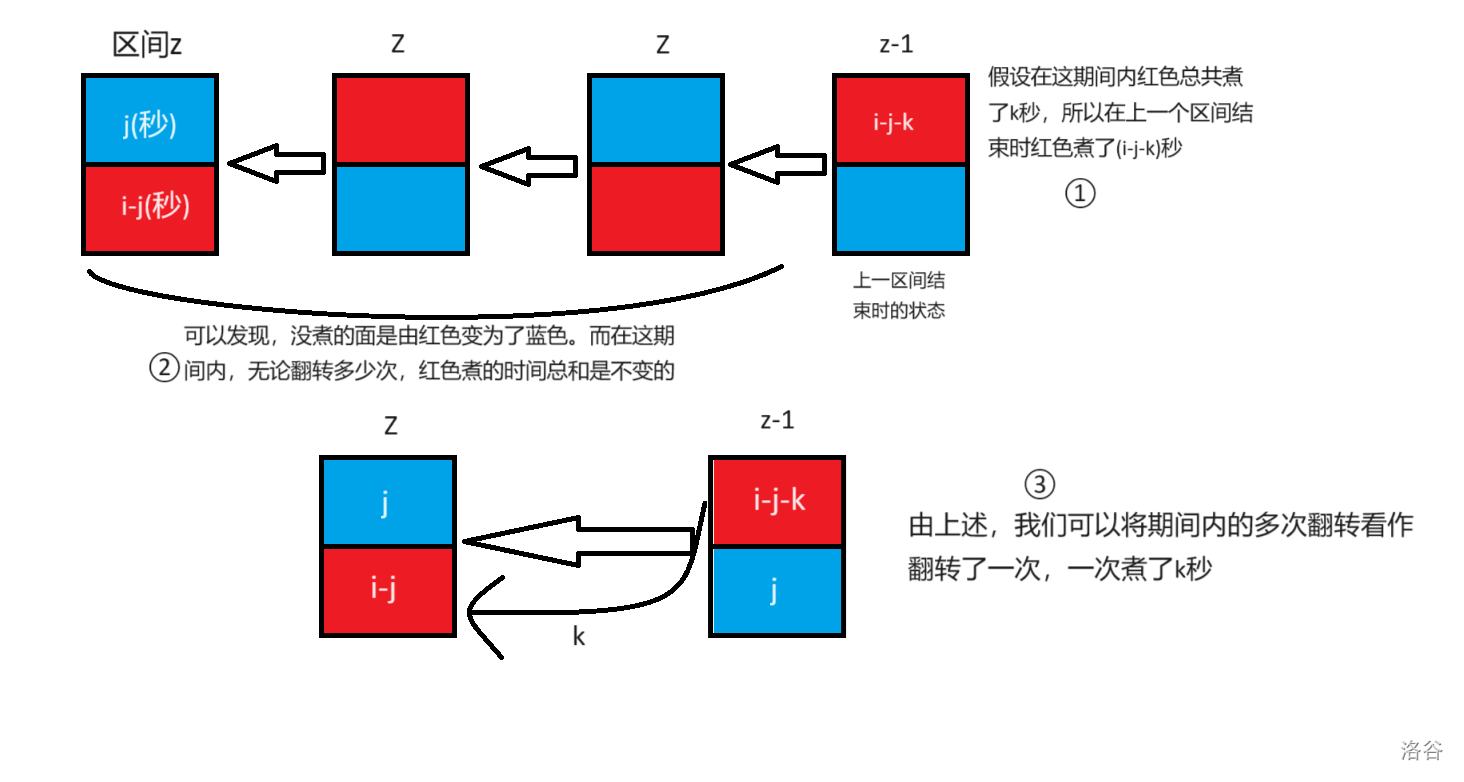
-
由图,可以得出转移 \(dp_{z,j} = \min ( dp_{z-1,i-j-k} ) +1\) 。
-
因为只能在区间 \(r_z\) 至 \(l_z\) 之内翻转,且结束时间为 \(r_{z}\) ,所以 $( r_{z}-k \ge l_{z} ) \to ( 0\le k\le r_{z}-l_{z}) $ ,并且满足 \(( r_{z} - j - k \ge l_{z} )\) 。
-
至于 \(j\) ,我们可以发现蓝色的枚举范围 $( 0 \le j \le r_{z} ) $ ,但如果再算上 \(k\) ,且两者都取最大值,那么 \(i-j-k\) 很可能会得到负数,造成越界,所以想用 暴力 拿部分分也是较为 困难 的。
-
因为所设状态为 区间结束时间 ,所以 \(i\) 无需枚举,为 \(r_z\) ,方程则变为 $ dp_{z,j} = \min \limits_{ 0 \le k \le r_{z} - l_{z} } ( dp_{ z-1,r_{z}-j-k } )+1$ 。
- 翻转 两次 :
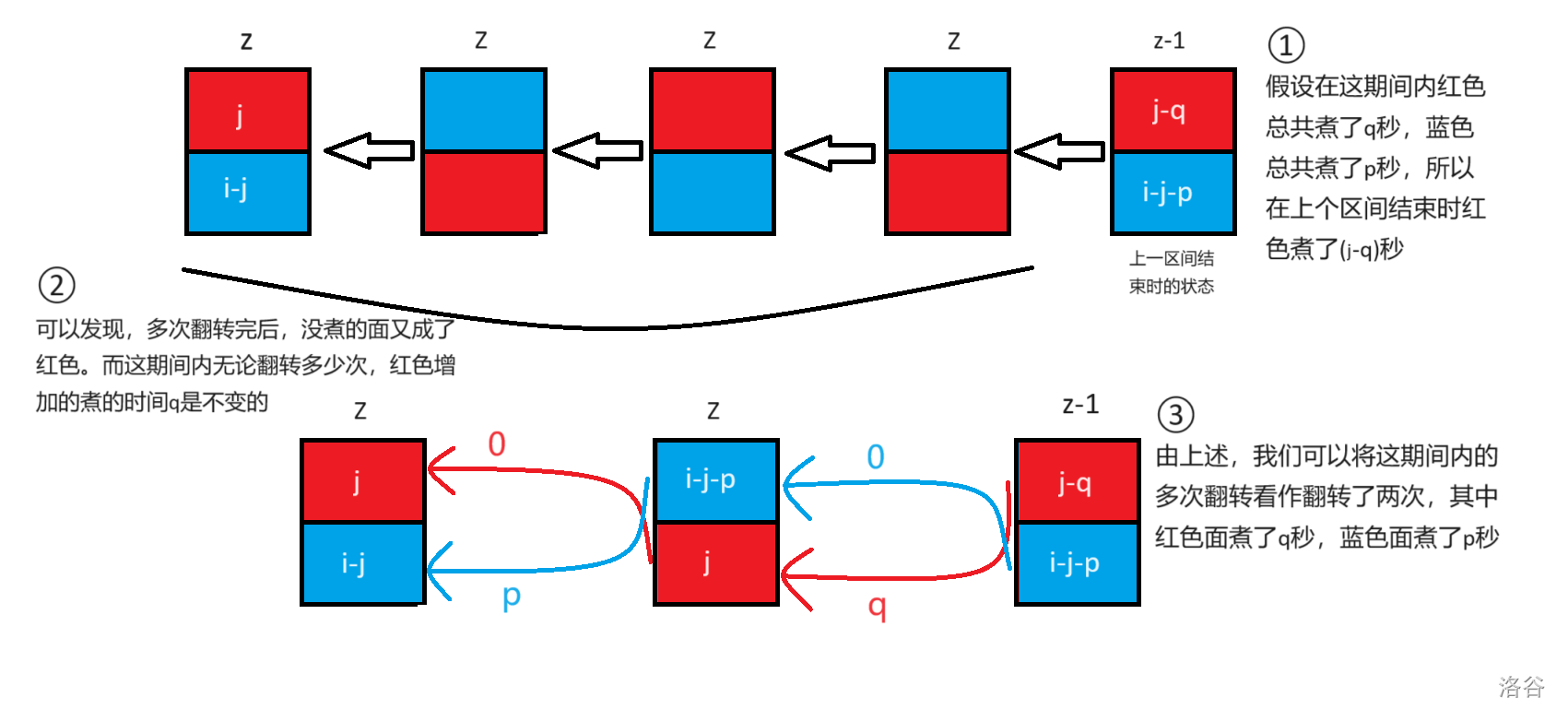
- 由图,可以得出转移 $ dp_{z,j} = \min ( dp_{z-1,j-q} )+2 $ ,同上 \(({ 0 \le q \le r_{z} - l_{z} })\) ,且满足 \(( l_{z} \le j-q \le r_{z} )\) 。
则所有 转移方程 如下(为了方便这里 \(i\) 为第 \(i\) 个区间):
\[dp_{i,j}=\begin{cases}dp_{i-1,j}&{0\le j\le r_{i}}\\ \min(dp_{i-1,r_{i}-j-k})+1&{0\le k\le r_{i}-l_{i}}\\ \min{(dp_{i-1,j-q})+2}&{0\le q\le r_{i}-l_{i}}\end{cases} \] -
优化
- 在分析翻转 一次 的方程时,我们发现用暴力跑 \(dp\) 是会越界的,且 \(( 0 \le n \le 10^5 )\) ,且枚举 \(j\) 与 \(k\) 也会 \(TLE\) 。那么,怎么办呢?
- 根据翻转 一次 和 两次 的方程中,我们可以发现,每当枚举到一个新的值,都会和原来的值取更小值,最终会取得这一区间内的最小值。每次更新,都会更新更小值,这是符合 单调性 的,所以可以使用 单调队列 进行优化。
- 由于变成在一个范围内取最小值,所以 \(k\) 和 \(q\) 取 最大范围 \(r_{i}-l_{i}\) 。
- 具体的,我们可以将翻转 一次 的方程看作在 $ dp_{ i-1,r_{i}-j-k } $ 到 \(dp_{ i-1,r_{i} }\) 之间取最小值,将翻转 两次 的方程看作在 $ dp_{i-1,j-q} $ 到 $ dp_{i-1,j} $ 之间取最小值(这里 $ r_{i}-j-k $ 化简后为 $ l_{i}-j $ ,它作为 出队条件 ,所以不用担心越界)。
- 则最终方程如下:
到了这,这题就解完了,欢迎指出题解中错误,如需代码也可以私我。
标签:方程,le,min,题解,Cutlet,区间,CF939F,dp,翻转 From: https://www.cnblogs.com/Kx-Triumphs/p/18377888