动态规划

总所周知，动态规划是一个肥肠重要的一个东西（对于算法竞赛而言）……
So，我们开始讲动态规划。

用的是 Luogu 官方题单：
https://www.luogu.com.cn/training/211#problems
以下也会依此顺序来讲解。。。

引子

Problem 1

https://www.luogu.com.cn/problem/P1216

[USACO1.5] [IOI1994]数字三角形 Number Triangles

题目描述

观察下面的数字金字塔。

写一个程序来查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。

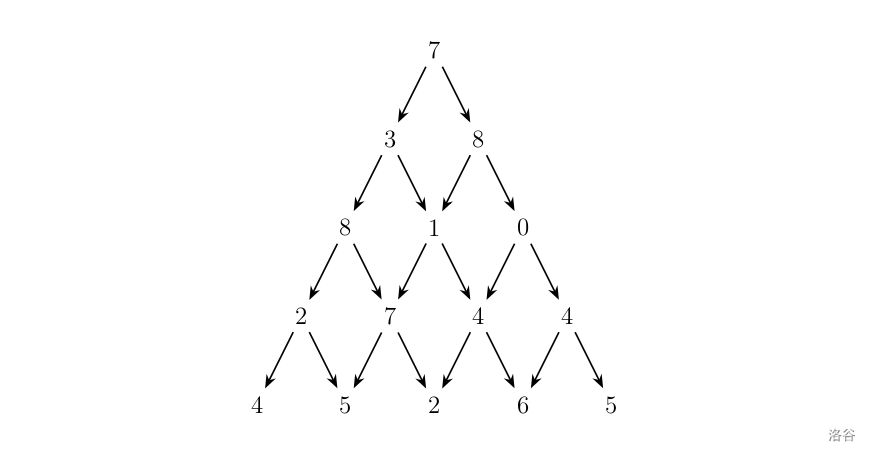
在上面的样例中，从 \(7 \to 3 \to 8 \to 7 \to 5\) 的路径产生了最大权值。

输入格式

第一个行一个正整数 \(r\) ,表示行的数目。

后面每行为这个数字金字塔特定行包含的整数。

输出格式

单独的一行,包含那个可能得到的最大的和。

样例 #1

样例输入 #1

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

样例输出 #1

30

提示

【数据范围】
对于 \(100\%\) 的数据，\(1\le r \le 1000\)，所有输入在 \([0,100]\) 范围内。

题目翻译来自NOCOW。

USACO Training Section 1.5

IOI1994 Day1T1

solve 1

Main idea--逆向求解。
正向难弄，就反向求解。

从下往上推，从倒数第二行开始，每一项的 \(f\) 数组记为到达此点的最大值

a[i][j]+=max(a[i-1][j-1],a[i-1][j]);//本题最重要的步骤 

So,\(ans\)就是\(f[1][1]\),输出即可。

code 1

#include<iostream>
using namespace std;
int n;
const int N=1000+5;
int a[N][N];
int f[N][N];
#define FOR(i,_l,_r) for(int i=_l;i<=_r;i++)
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cin>>n;
	FOR(i,1,n)
		FOR(j,1,i){
			cin>>a[i][j];
			f[i][j]=a[i][j];
		}
	for(int i=n-1;i;i--){
		for(int j=1;j<=i;j++){
			f[i][j]=max(a[i][j]+f[i+1][j],a[i][j]+f[i+1][j+1]);
		}
	}
	cout<<f[1][1]<<endl;
	return 0;	
}

So easy,right?
这只是一个小热身。

problem 2

https://www.luogu.com.cn/problem/P1048

[NOIP2005 普及组] 采药

题目描述

辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”

如果你是辰辰，你能完成这个任务吗？

输入格式

第一行有 \(2\) 个整数 \(T\)（\(1 \le T \le 1000\)）和 \(M\)（\(1 \le M \le 100\)），用一个空格隔开，\(T\) 代表总共能够用来采药的时间，\(M\) 代表山洞里的草药的数目。

接下来的 \(M\) 行每行包括两个在 \(1\) 到 \(100\) 之间（包括 \(1\) 和 \(100\)）的整数，分别表示采摘某株草药的时间和这株草药的价值。

输出格式

输出在规定的时间内可以采到的草药的最大总价值。

样例 #1

样例输入 #1

70 3
71 100
69 1
1 2

样例输出 #1

3

提示

【数据范围】

• 对于 \(30\%\) 的数据，\(M \le 10\)；
• 对于全部的数据，\(M \le 100\)。

【题目来源】

NOIP 2005 普及组第三题

solve 2

思路1：
1.定义二维数组 , \(f[i][j]\)表示采第i株药,花费时间\(j\)可以采到的草药的最大总价值。
2.输入采摘某株草药的时间和这株草药的价值。
3.判断是否采摘这株草药
if 不摘

    f[i][j]=f[i-1][j];

else if 摘

f[i][j] = f[i - 1][j - ti[i]] + val[i] ;

这里需要注意 : 如果当前采摘这株草药获得的价值比采摘i-1株草药的价值低的话也不摘。
所以需要比较。
因此无论摘不摘这一株草药,一开始的价值都应该是采摘i-1株草药的价值。
So

f[i][j] = max(f[i][j], f[i - 1][j - ti[i]] + val[i]) ;

相当于初始化当前可以获得的价值为采摘i-1株草药的价值，只有背包容量足够采摘当前这一株草药的时候,才判断是否采摘当前的这一株草药。
After that

	f[i][j] = f[i - 1][j] ;
	if(j >= ti[i]) 
		f[i][j] = max(f[i][j], f[i - 1][j - ti[i]] + pri[i]) ;

4.输出答案

code 2-1

#include<bits/stdc++.h>
using namespace std;
int T;
int M;
const int N=105;
int f[N][(int)1000+5];
int ti[N];
int val[N];
#define FOR(i,_l,_r) for(int i=_l;i<=_r;i++) 
int main()
{
	cin>>T>>M;
	FOR(i,1,M){
		cin>>ti[i]>>val[i];
		FOR(j,1,T){
			f[i][j]=f[i-1][j];
			if(j>=ti[i])
				f[i][j]=max(f[i][j],f[i-1][j-ti[i]]+val[i]);
		} 
	}
	cout<<f[M][T]<<endl;
	return 0;
}

思路2

相比于第一种思路,最大的不同就是使用的是一维数组而不是二维数组,不记录\(i\)，只记录花费的时间\(j\)，其他的都与二维数组的思路没有什么太大的不同(这就是滚动数组呢……)
注意，是从后往前滚的。。。
贴code啦

code 2-2

#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int f[N];
int ti[N];
int val[N];
int T,M;
#define FOR(i,_l,_r) for(int i=_l;i<=_r;i++)
int main()
{
	cin>>T>>M;
	FOR(i,1,M)  cin>>ti[i]>>val[i];
	FOR(i,1,M)
		for(int j=T;j;j--){
			if(j>=ti[i]){
				f[j]=max(f[j],f[j-ti[i]]+val[i]);
			}
		}
	cout<<f[T]<<endl;
	return 0;	
}

做完了吧，是不是很简单，其实这就是一个01背包的板子……

这是第一天，讲累了，剩下的以后再讲吧。