本题题意
小 A 和小 B 在一个 \(n \times n\) 的棋盘里下柯基棋,当一个人不能再放下棋子时,他就输了。问谁会有必胜策略。
思路
先不考虑小 C 的捣乱。
分类讨论
- 当 \(n\) 为奇数时,不难得出:当小 A 第一步放在棋盘的正中心时,以后不管小 B 放在哪里,小 A 只要放在它的对称处就行了。这样子,当棋盘上下不了棋子时,正好是小 B 的回合。
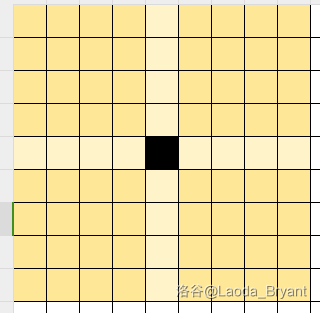
第一步,小 A 下在正中心,其所在行和列为该棋盘的对角线。
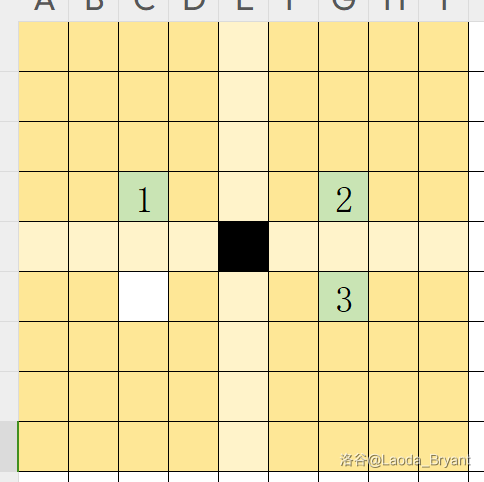
第二步,小 B 下。到第三步时,小 A 可以下在图中标注的位置,这里我们选择 \(1\) 号位置。
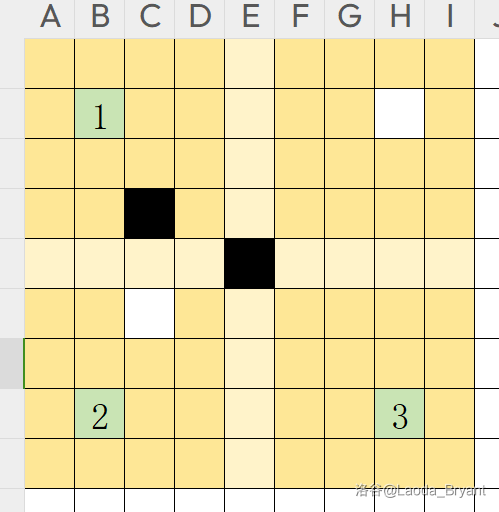
第四步,小 B 下。由于其对称性,小 B 可以放在标注的地方。但由于刚才确定了对称轴是第五列,所以放在 \(3\) 号位置。
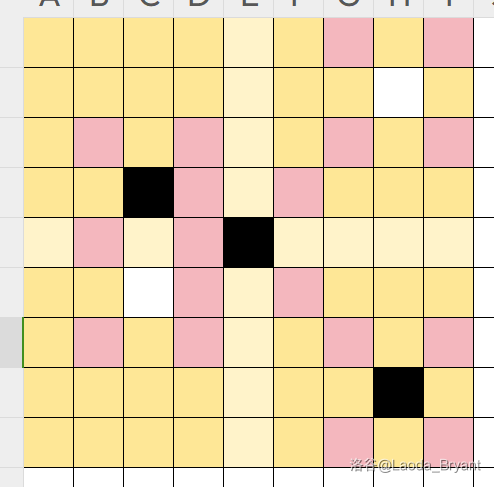
这里我们把未放置棋子但不能放棋子的格子用红色标记出来。

接着走。

最后,在棋盘不能放置棋子时,是偶数步,小 B 的回合,因此小 B 输了,小 A 赢了。
- 当 \(n\) 为偶数时,不管小 A 下在哪里,小 B 也只要它的放在对称处。这样子,当棋盘上下不了棋子时,正好是小 A 的回合。
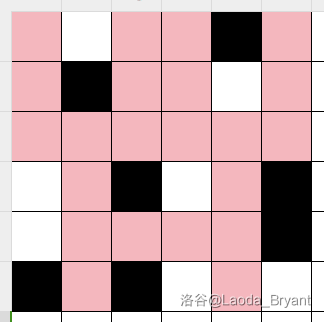
这里,对称轴是第 \(3\) 个格子和第 \(4\) 个格子之间的边界线。由于现在是奇数步,是小 A 的回合,故此小 B 获胜。
再来说小 C
根据小 C 每次捣乱的之后棋盘边长增加 \(2\),可得知 \(n\) 的奇偶性性是不变的。又因为 x[i]=x[i-1]+((xor_shift(seed)%(unsigned long long)(2*2)+1))*2;,可知每次捣乱时是都是在偶数步,所以先后顺序不变。
AC code
#include<bits/stdc++.h>
//#define endl '\n'
using namespace std;
int main(){
int T;
cin>>T;
while(T--){
int n,q,seed;
cin>>n>>q>>seed; 虽然q和seed没有对棋盘产生任何变化,但该输的还是要输
if(n%2==1) cout<<"A won"<<endl; A可以放在正中间则可以嬴
else cout<<"B won"<<endl;
}
return 0;
}