题解：CF644A Parliament of Berland

本题题意

有 \(n\) 个议员，编号为 \(1 \sim n\)，就坐在 \(a \times b\) 的礼堂里，求如何安排座位能够使得任意两个相邻的座位上的议员奇偶性不相同。

思路

无解情况

当 \(n > a \times b\) 时，必定无法满足，则直接输出 -1。

有解情况

打表找规律。


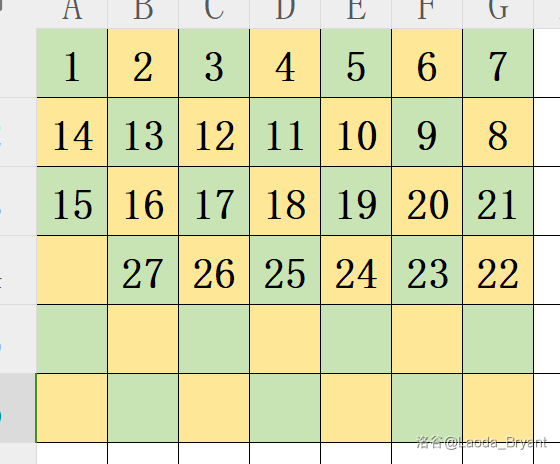
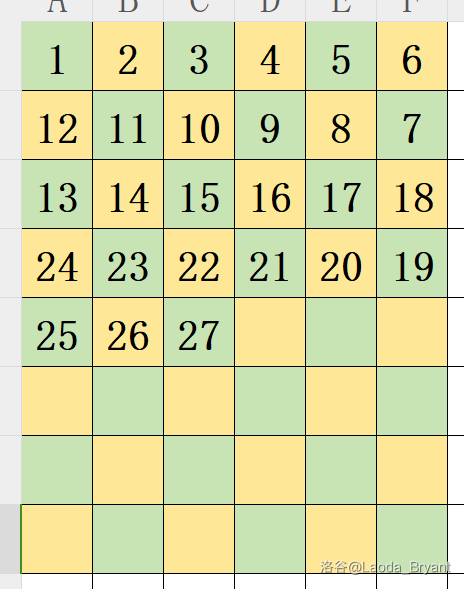
我们发现，只要让奇数行正着就坐，偶数行反着就坐，即可安排完全部议员。

AC code

#include<bits/stdc++.h>
using namespace std;
int n,a,b,s[105][105],g;
int main(){
	cin>>n>>a>>b;
	if(n>a*b){
		cout<<-1;
		return 0;
	}
	g=1;
	for(int i=1;i<=a;i++){
		if(g>n) break; 
		if(i%2==1){ //正着安排 
			for(int j=1;j<=b;j++){
				if(g>n) break;
				s[i][j]=g;
				g++;
			}
		}else{
			for(int j=b;j>=1;j--){ //反着安排
				if(g>n) break;
				s[i][j]=g;
				g++;
			}
		}
	}
	for(int i=1;i<=a;i++){
		for(int j=1;j<=b;j++){
			cout<<s[i][j]<<" ";
		}
		cout<<endl;
	}
	return 0;
}