P1543 [POI2004] SZP 题解
题目简述
有 \(n\) 个人,每个人都会监视另一个人,要求选出尽可能多的同学,使得选出的每一名同学都必定会被监视到。且选出的同学不可再监视其他人。
思路简述
因为任意一个人只能被另一个人管,那么就想到,如果没人管的同学就不能被选(不被监视)。
若某个人有多个人监视,且监视他的有至少一个专门监视(监视他的那个人没人监视)则他不得不去。
那么再看看如果出现环咋办。
不如画个图理解。
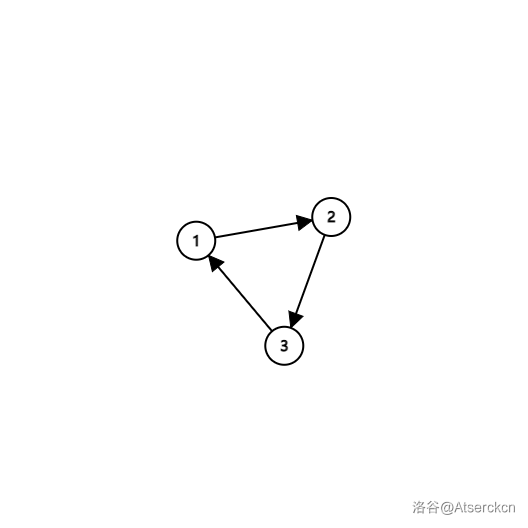
上图即为一个环:\(1\) 监视 \(2\),\(2\) 监视 \(3\),\(3\) 监视 \(1\)。
那么不妨枚举一下。
如果派出 \(1\),则 \(3\) 可以监视到,而 \(2\) 也可以监视到 \(3\),完美符合题意。
但是,若取出了 \(1\) 和 \(2\),\(2\) 则会没人监视(本来监视他的 \(1\) 号走了)。
所以可以得出结论:若遇到环,设 \(s\) 为环的节点个数,则取出的个数为 \(\lfloor\frac{s}{2}\rfloor\)。
代码实现
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int n,to[N],ans,cnt_ring,in[N];
bool gone[N]/*被选中了吗*/,vis_ring[N]/*遍历过了吗*/;
queue<int > q;//注意:这里的q可不是说进队列了就得被选中
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&to[i]);
++in[to[i]];//入度+1
}
for(int i=1;i<=n;i++)
if(!in[i])//拓扑排序老板子
q.push(i);
while(!q.empty())
{
int t=q.front();q.pop();
vis_ring[t]=true;//判断是否遍历过
if(gone[t])//他走了,他监视的同学就看看情况
{
if((--in[to[t]])==0)
q.push(to[t]);
}
else//他没走,他监视的孩子可就遭老罪喽
{
if(!gone[to[t]])//孩子没走
{
++ans;
gone[to[t]]=true;//给我走
q.push(to[t]);
}
}
}
for(int i=1;i<=n;i++)//开始判环
{
if(!vis_ring[i]&&in[i])
{
cnt_ring=0;//作用如其名
for(int j=i;!vis_ring[j];j=to[j])
{
++cnt_ring;
vis_ring[j]=true;
}
ans+=cnt_ring/2;//刚说的,不过C++自动向下取整
}
}
printf("%d\n",ans);
return 0;
}