Update Data

• \(\mathrm{Update} \ 2024.8.19\) : 因为 \(\KaTeX\) 打不出异或及逻辑与的符号，所以用单行代码块来代替，如 ^ ，&& 等。

4.计算机的信息编码和基本运算

4.1 计算机的信息编码

4.1.1 ASCII码

• ASCII 码，即美国标准信息交换吗，用于表示常见的英文字母，数字和常用符号。
• ASCII 码的取值范围是 \(0-127\) , 可以用 \(7\) 个 bit 表示。

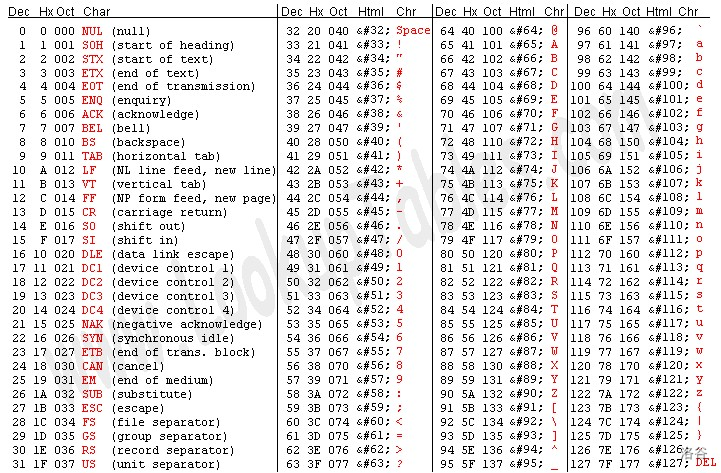
• 这张表看上去似乎很复杂，但是我们只需记住三个点：
  • \(0-9\) 对应数字 \(48-57\) ；
  • \(a-z\) 对应数字 \(97-122\) ；
  • \(A-Z\) 对应数字 \(65-90\) ；
  • 所以如果你要快速知道字符的 ASCII 码，以小写字母为例，只需要将小写字母的字典序 \(x+97-1\) 即为所求字母的 ASCII 码，其余同理。
  • 另外，空格键的 ASCII 码是 \(32\) ，换行符的 ASCII 码是 \(13\) 。
  • 外码和内码：
    • 外码即为计算机现实的字符，如 \(A\) ；
    • 内码是计算机内部存储的代码，如 \(a\) 对应的 ASCII 码为 \(97\) ；

4.1.2 国标码（GB码）

• GB码是中文在计算机中用的编码。现时中华人民共和国官方强制使用 GB18030 标准，但较旧的计算机仍然使用 GB 2312。

• 在之前的 GB1312标准中，采用 \(2\) 个字节对汉字进行编码，并根据使用拼读将汉字分为一级汉字（按拼音排序）和二级汉字（按部首排序）。

• 另外，中文字符的标点分为全角标点（占 \(2\) 个字节）和半角标点（占 \(1\) 个字节）。

• 中文的输出方法是字形码。

  

  为了将汉字显示或打印出来，我们将汉字按图形符号设计成点阵图（一个点是一个 bit），就得到了字形码，一般采用 \(16 \times 16\) 点阵或 \(24 \times 24\) 点阵或 \(48 \times 48\) 点阵，由此可以计算出一个汉字所占的空间。

4.1.3 统一码（Unicode）

• 统一码是为了解决传统字符编码方案的局限而产生的，它为每种语言中的每个字符设定了同意并且唯一的二进制编码以满足跨语言、跨平台进行文本转换的需求。
• Unicode字符集可以简写成 UCS，UCS-2 用两个字符编码，UCS-4 用4个字节编码。现在常见的方案有 UTF-8、UTF-16等等。

4.2 计算机逻辑运算

4.2.1 与、或、非、异或（ 对于二进制 \(0\) 和 \(1\) ）

• 非运算：
  • 非运算可以写作 \(!\) ， \(\lnot\) ， $\mathrm{not} $ 。
  • 非运算就是取反，如 \(! \ 0=1\) , \(! \ 1=0\) 。
• 与运算
  • 与运算可以写作 \(\&\) ， \(\cap\) ， $\wedge $ ， $\mathrm{and} $ .
  • 进行与运算的两个数，如果数值都为 \(1\) 结果为 \(1\) ；
  • 如果数值都为 \(0\) 结果为 \(0\) ；
  • 如果数值不相同，则结果为 \(0\) ；
• 或运算
  • 或运算可以写作 \(|\) ， $\mathrm{or} $ ， \(\vee\) ，$\cup $ ；
  • 进行与运算的两个数，如果数值都为 \(1\) 结果为 \(1\) ；
  • 如果数值都为 \(0\) 结果为 \(0\) ；
  • 如果数值不相同，则结果为 \(1\) ；
• 异或运算
  • 异或运算可以写作 \(\mathrm{xor}\) , \(\oplus\) , ^ ;
  • 进行与运算的两个数，如果数值都相同结果为 \(0\) ；
  • 如果数值不同结果为 \(1\) 。
• 注意区分异或运算 ^ 和与运算 $\wedge $ 。
• 另外，在 C++ 语言中，我们把 \(\mathrm{true}\) 标记为 \(1\) , 把 \(\mathrm{false}\) 标记为 \(0\) 。
• 还有，在 C++ 语言中，运算优先级为：括号 \(>\) 非 \(>\) 乘除模 \(>\) 加减 \(>\) 左移右移 \(>\) 大于小于判断 \(>\) 等于判断 \(>\) \(\&\) \(>\) ^ \(>\) \(|\) \(>\) && (逻辑与) \(>\) \(||\) (逻辑或)同级别从左往右依次计算。
  注意在 C++ 中，基本运算中的 \(\&\) 和逻辑与是不一样的。

4.2.2 进制

• 进制即进位计数制。我们一般用的是十进制。使用 \(0-9\) 这些符号，满足逢十进一。
• 计算机采用二进制，只使用 \(0\) 和 \(1\) 两种符号，逢二进一，可以用 \((X)_2\) 表示一个二进制数 \(X\) 。
• 除了十进制和二进制，常见的还有八进制和十六进制，八进制使用 \(0-7\) 这些符号，逢八进一；十六进制不但使用 \(0-9\) 这些符号，还用字母 \(A\)，\(B\)，\(C\)，\(D\)，\(E\)，\(F\) 来表示十进制下的 \(11\)，\(12\)，\(13\)， \(14\)，\(15\) ，满足逢十六进一 。一般用 \((X)_8\) 和 \((X)_{16}\) 表示八进制和十六进制。
• 因此，一般地，对于 \(N\) 进制，满足逢 \(N\) 进一，可以用 \((X)_N\) 表示 \(N\) 进制下的数字 \(X\) 。
• 此外，还有其他表达方法：
  • \(BIN\) 或 \(B\) ：表示二进制；
  • \(OCT\) 或 \(O\) ：表示八进制；
  • \(DEC\) 或 \(D\) ：表示十进制；
  • \(HEX\) 或 \(H\) ：表示十六进制。
  • 有些时候会用数字 \(0\) 开头表示一个八进制数，比如 \(077=(77)_8\)
  • 用 \(0x\) 或 \(0X\) 开头表示一个十六进制数，如 \(0xff\)， \(0X3F\) 。

4.2.3 进制转换

• 整数部分 \(X\) 进制转换为 \(10\) 进制：

  • 按位展开求和：如 \((1011)_2\) :

    1	0	1	1
    \(2^3\)	\(2^2\)	\(2^1\)	\(2^0\)

    所以 \((1011)_2=1 \times 2^0+1 \times 2^1+0 \times 2^2+1 \times 2^3=11\) .
    因此，一般的，按位展开求和的公式写作 ( 把最低位看成 \(X_1\) )：

    \((X_i)_N=X_1 \cdot N^0+X_2 \cdot N^1+X_3 \cdot N^2+\cdot\cdot\cdot+X_i \cdot N^{i-1}\ (i>=0)\) .

  • 从高位到低位逐位运算：
    如： \((1011)_2=((1 \times 2+0) \times2+1) \times 2+1=11\) .
    因此，一般地，从高位到低位逐位运算公式可以写成 ( 把最高位看作 \(X_i\) )：

  \[(X_i)_N=((((X_i \cdot N+X_{i-1})\cdot N+X_{i-2}) \cdot N+X_{i-3}) \times\dots+\dots) \cdot N+X_{i-(i-1)} \]

• 十进制转 \(X\) 进制 ：除 \(X\) 取余法（不停地\(\mod X\) , 然后倒序输出）。

• 小数部分 \(X\) 进制转换为 \(10\) 进制：

  • 按位展开求和：

  1	0 .	1	1
  \(2^1\)	\(2^0\)	\(2^{-1}\)	\(2^{-2}\)

  所以 \((10.11)_2=1 \times 2^1+0 \times 2^0+1\times 2^{-1}+1 \times 2^{-2}=2.75\)
  因此，一般的，对于小数部分的按位展开求和公式为 (把小数点最后一位看做 \(X_1\) )：

  \[(X_i)_N=X_1 \cdot N^i+X_2 \cdot N^{i+1}+X_3 \cdot N^{i+2}+ \cdot\cdot\cdot+X_i \cdot N^{i+(i+1)}\ (i<0) \]

• 小数部分 \(10\) 进制转换为 \(X\) 进制：

  • 乘 \(X\) 取整法：
    即小数部分不停地乘 \(X\) ，结果保留整数，然后顺序输出。
  • 注意，小数部分 \(10\) 进制转换为 \(X\) 进制的结果可能不是一个有限小数。

• 部分特殊情况：

  • 八进制和十六进制转二进制：
    因为 \(8=2^3\) , 所以八进制转二进制的方法就是每一位拆成三位。
    因为 \(16=2^4\) , 所以十六进制转二进制的方法就是每一位拆四位。
  • 二进制转八进制或十六进制：
    同理，因为 \(8=2^3\) , 所以二进制转八进制的方法就是每三位合成一位。
    因为 \(16=2^4\) , 所以二进制转十六进制的方法就是每四位合成一位。

• 所以为了方便运算，我们需要记住 \((1-15)_{10}\) 转换为二进制的值。

  \(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)	\(8\)	\(9\)	\(10(A)\)	\(11(B)\)	\(12(C)\)	\(13(D)\)	\(14(E)\)	\(15(F)\)
  \(1\)	\(10\)	\(11\)	\(100\)	\(101\)	\(110\)	\(111\)	\(1000\)	\(1001\)	\(1010\)	\(1011\)	\(1100\)	\(1101\)	\(1110\)	\(1111\)

• 注意，对于二进制转八进制，如果整数部分（或小数部分）的位数不是 \(3\) 及三的倍数，需要在最高位（小数部分是最低位）前补上 \(1-2\) 个 \(0\) 。如 \((1011101.10111)_2=(001\ 011\ 101.101\ 110)_2=(135.56)_{10}\)

• 对于二进制转十六进制则同理。如 \((1011101.10111)_2=(0101 \ 1101.1011\ 1000)=(5D.B8)\)

• 以上是一些简便方法，对于一般情况下， \((A)_X\) 转换为 \((A)_Y\) , 需要十进制作为桥梁来进行进制之间的转换。

4.2.4 进制的运算

• 相同进制 \((X)\) 下的运算：
  • 对于加法，满 \(X\) 进一；
  • 对于减法，借一还 \(X\) 。
• 不同进制下的运算：
  • 把不同进制的数转化为十进制，再按十进制运算法则运算即可。

4.2.5 位运算

• 一个非负整数进行与、或、异或运算方法：
  • 把非负整数转换为二进制数（它的源码，复数要转换成补码），然后逐位进行运算即可。

4.2.6 源码、补码和反码

• 在 C++ 中，对于 int 型的变量在计算机中会用 \(32\) 个 bit 来进行存储。其中第一位（符号位）代表数字的正负（ \(0\) 表示正数， \(1\) 表示负数），其余 \(31\) 位用来记录数字的绝对值。
• 一个数字直接转换成二进制后得到的 \(01\) 序列成为它的源码。
• 将原码的每一位取反即为反码，正数源码的反码是它本身。
• 用源码计算十分复杂，因此计算机存储的是一个数字的补码。
• 对于正数，它的补码就是源码。
• 对于负数，它的补码是再付号位不变的情况下，取反剩下的序列在加 \(1\) 得到的。
• 另外，位运算是对补码的每一位进行运算。因此负数的位运算要单独考虑。要得到负数的源码并转换成补码参与运算，并将运算之后的补码转化成源码在转换成 \(10\) 进制。