标签：增广 int 网络笔记最小学习 dep 流量 rightarrow

网络流学习笔记

一、定义

网络（network）是指一个特殊的有向图 \(G=(V,E)\)，其与一般有向图的不同之处在于有容量和源汇点。

\(E\) 中的每条边 \((u, v)\) 都有一个被称为容量 (capacity) 的权值，记作 \(c(u, v\))。当 \((u,v)\notin E\) 时，可以假定 \(c(u,v)=0\)。

这句话的意思是对于网络流中的反向边，流量应为 \(0\)。

\(V\) 中有两个特殊的点：源点（source）\(s\) 和汇点（sink）\(t\)（\(s \neq t\)）。
对于网络 \(G=(V, E)\)，流（flow）是一个从边集 E 到整数集或实数集的函数，其满足以下性质。

容量限制：对于每条边，流经该边的流量不得超过该边的容量，即 \(0 \leq f(u,v) \leq c(u,v)\)。

流守恒性：除源汇点外，任意结点 \(u\) 的净流量为 \(0\)。其中，我们定义 u 的净流量为 \(f(u) = \sum_{x \in V} f(u, x) - \sum_{x \in V} f(x, u)\)。

流出多少，也应该流入多少。

对于网络 \(G = (V, E)\) 和其上的流 \(f\)，我们定义 \(f\) 的流量 \(|f|\) 为 \(s\) 的净流量 \(f(s)\)。作为流守恒性的推论，这也等于 \(t\) 的净流量的相反数 \(-f(t)\)。

\(s\) 是源点， \(f(s)\) 是 \(s\) 流出的流量，就等于 \(t\) 流入的流量 \(f(t)\)。

斜对称性：对于每条边，\(f(u,v)=-f(v,u)\)。

这是后文反向边与反悔策略需要用到的。

对于网络 \(G = (V, E)\)，如果 \(\{S, T\}\) 是 \(V\) 的划分（即 \(S \cup T = V 且 S \cap T = \varnothing\)），且满足 \(s \in S, t \in T\)，则我们称 \(\{S, T\}\) 是 \(G\) 的一个 \(s-t\) 割（cut）。我们定义 s-t 割 \(\{S, T\}\) 的容量为 \(||S, T|| = \sum_{u \in S} \sum_{v \in T} c(u, v)\)。

割通俗来讲就是将一张网络断掉一些边使得其不再连通的的边集。割的容量就是这个边集的流量和。

二、最大流问题

1. 最大流算法

(1) 增广路

增广路指的是原图中一条 \(s\rightarrow t\) 且沿途 \(c(u,v)\) 均 \(>0\) 的路径。

(2) FF 算法

在原图中每一次找到一条增广路进行增广，直到原图中不存在增广路。

(3) 反向边与撤销影响

是对上面的算法正确性的一个证明。显然每一次增广路的选择是偶然的。

考虑这样一张网络：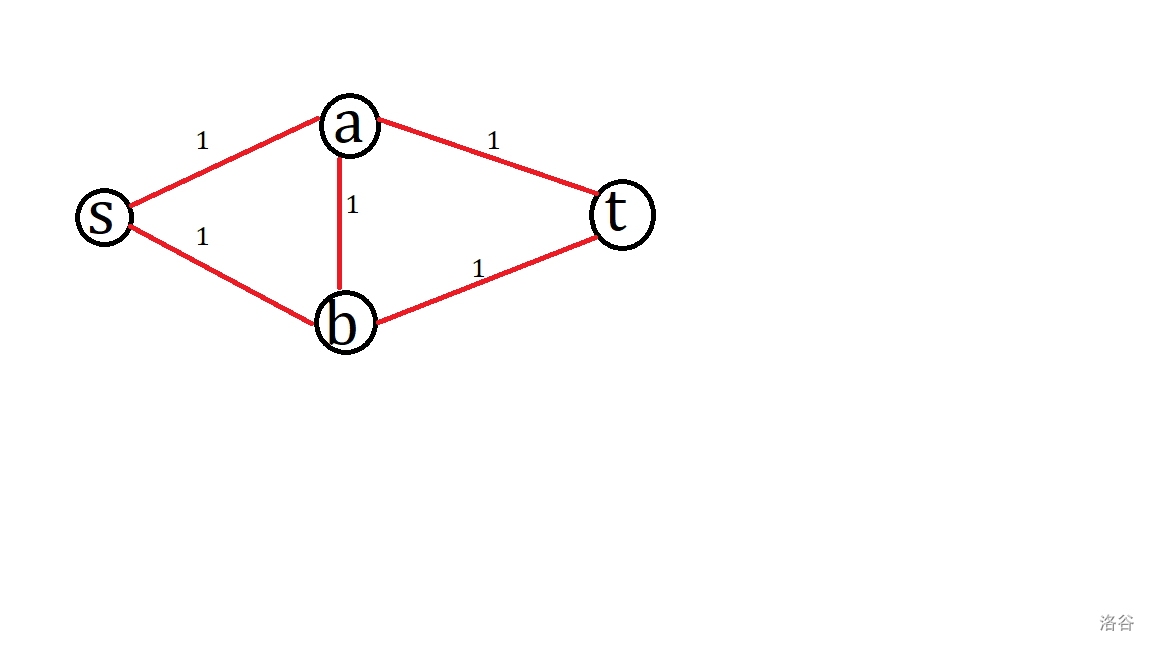
显然最优方案是 \(s\rightarrow a \rightarrow t,s\rightarrow b\rightarrow t\)。但如果找到的增广路是 \(s\rightarrow a \rightarrow b \rightarrow t\) 呢？

由于网络流斜对称性质，此时的流量 \(f(a,b)=1,\) 则 \(f(b,a)=-1\)。那么剩余流量 \(c(b,a)'=c(b,a)-f(b,a)=1\)，不难发现此时原图有一条 \(s\rightarrow b \rightarrow a \rightarrow t\) 的增广路。

考虑这样做的实际意义：\(b\rightarrow t\) 的流量实际由 \(s\rightarrow b\) 来最终承担了，而 \(a\rightarrow t\) 的流量实际由 \(s\rightarrow a\) 承担。\(a\rightarrow b\) 本身不承担任何意义，只是过渡使用。

于是我们证明了 FF 算法的正确性。

(4) EK 算法

每次通过 bfs 找到一条增广路，进行增广。是对 FF 算法的一个具体实现。

(5) Dinic 算法

最大流问题中最常用的算法，下面描述该算法的步骤。

对原图依据每个点到源点的距离 \(dep_x\) 进行 bfs 分层，暂时删除 \(dep_v<dep_u\) 的边 \((u, v)\)。
对原图进行 dfs 找到增广路
重复上面算法直到源汇点不再连通。

考虑上面算法的正确性：显然。本质上是通过临时删边的方式使得每一次找到一个流使得原图不再连通，而找到流的顺序并不影响最大流的大小。

(6) Dinic 算法的优化

无用节点删除：若从一个点 \(x\) 出发无法继续增广，令 \(dep_x=\infty\)，即变相删除 \(x\)。
当前弧优化：从一个点 \(x\) 增广后可能有很多点 \(y\) 有\(c(x,y)=0\)，显然这些点在后续中无用，那么我们每次增广时标记 \(x\) 点之后第一个有用的点记为 \(cur_y\)，下次增广时从它开始遍历即可。

经过优化后的 Dinic 时间复杂度上界是 \(O(V^2E)\)，但实际运用中往往远远不可达这个上界，因此引用 Dyc780511 的一句话：

我们通常认为 Dinic 的时间复杂度是 \(O(玄学)\)。

参考代码：

int cur[N], dep[N];
int bfs() {
	for (int i = 1; i <= n; i++)
		dep[i] = inf;
	queue<int>q;
	q.push(s);
	cur[s] = head[s];
	dep[s] = 0;
	while (!q.empty()) {
		int x = q.front();
		q.pop();
		for (int i = head[x]; i; i = e[i].nxt) {
			int y = e[i].to;
			if (e[i].val > 0 && dep[y] == inf) {
				q.push(y);
				cur[y] = head[y];
				dep[y] = dep[x] + 1;
				if (y == t)
					return 1;
			}
		}
	}
	return 0;
}
int dfs(int x, int sum) {
	if (x == t)
		return sum;
	int k, flow = 0;
	for (int i = cur[x]; i && sum; i = e[i].nxt) {
		int y = e[i].to;
		if (e[i].val > 0 && dep[y] == dep[x] + 1) {
			k = dfs(y, min(sum, e[i].val));
			if (k == 0)
				dep[y] = inf;
			e[i].val -= k;
			e[i ^ 1].val += k;
			sum -= k;
			flow += k;
		}
	}
	return flow;
}
int dinic() {
	int ans = 0;
	while (bfs())
		ans += dfs(s, inf);
	return ans;
}

2. 最大流建模技巧

(1) 拆点

例1：[SCOI2007] 蜥蜴

显然 \(ans=\) 总蜥蜴数 \(-\) 最大流。考虑如何限制每个石柱的高度。将石柱拆成入点和出点，在两点之间连流量为石柱高度的边即可。

路径问题拆出入点是一个常用的思路。

例2：[HNOI2007] 紧急疏散

考虑如何处理“每一秒只能有一个人离开”。将每个门 按照时间 拆成一些个点，把这些个点和汇点 \(t\) 连边权为 \(1\) 的边，每个人向到达门所用时间的那个点连边权为 \(1\) 的边，同一个门每个时间之间连流量为 \(\infty\) 的边即可。

按照时间拆点不常见，但是要掌握这个 \(\text{trick.}\)

(2) 二分图

例1：SDOI2015 星际战争

考虑二分时间，将机器人放在一边，武器放在一边，相互连边描述每一个状态即可。

例2：SCOI2012 奇怪的游戏

方格题考虑 黑白染色。黑白染色的目的是把点分为两类，构成一个二分图来网络流。然后按照奇偶性分类，用网络流来 \(\text{check}\) 即可。

注意数学问题 按照奇偶性分类是一个极为常用的做法，本质目的是为了构成一个二分图好跑网络流。

三、最小割问题

1. 最大流最小割定理

(1) 内容

对于任意一张网络，其最大流等于最小割。

(2) 证明

引理：对于一张网络，其任意一个割均 \(\ge\) 最大流。

证明：假设该网络有一个割 \(<\) 最大流。那么这个网络不再连通，无法找到增广路。由最大流的定义，该网络的最大流就是这个割。结合假设，这个假设是矛盾的，原命题成立。那么最小割一定 \(\ge\) 最大流。

现在考虑如何证明其能取到最大流。

当原图跑到最大流时，原图不存在增广路。那么在最大流的每一个流中总有流量最小的边为 该流的流量限制，这些边流量相加即为最大流，同时这些边也可以组成一个最小割。

于是当我们想求出最小割时，求出原网络最大流即可。

2. 最小割建模技巧

(1) 环式建模

以我所见，最小割的建模通常是环式建模，而环式建模通常有两种。我称一种为“双环式”，另一种为“单环式”，其中“双环式”较为简单暴力，好想但时间复杂度高；“单环式”需要解方程，时间复杂度更优。以我所见，选择“双环式”建模的人更多一些。

两种建模我均选择 [国家集训队] happiness 讲解。这道题的基本思路是先假设全部满足，一边为文科，一边为理科建出二分网络，求出最小割使得每个人只能选择其中一边。

a. 双环建模

双环建模大多数长这个样子：

其中 \(i,j\) 是原图中需要建的点，\(p,q\) 是辅助点，用来描述 \(i,j\) 之间处于同一侧的权值。具体地，\(s\rightarrow i,i\rightarrow t,s\rightarrow j,j\rightarrow t\) 分别赋予 \(i,j\) 不处于 \(s\) 或 \(t\) 集合的流量，\(s\rightarrow p,q\rightarrow t\) 连流量为 \(i,j\) 不同时属于 \(s\) 或 \(t\) 集合的损失的边，\(p\rightarrow i,i\rightarrow q,p\rightarrow j,j\rightarrow q\) 赋予 \(\infty\) 的流量，这样建图 一目了然，十分直观，不容易出锅 ；但缺点是若原先就有 \(n\) 个点，这样建图之后会有约 \(n^2\) 级别的点，复杂度不优。

注意根据题意分析，有时有些边是不用连的。

b. 单环建模

单环建模大多数长这个样子：

我们分别计算切断每组边的损失。令 \(s\) 为文科，\(t\) 为理科，选文科的收益分别为 \(p_i,p_j\)，选理科的收益分别为 \(q_i,q_j\)，都选理科的收益为 \(m\)，都选文科的收益为 \(n\)。

由题意可以列出方程：

\[\begin{cases} a+c&=q_i+q_j+m \\ b+d&=p_i+p_j+n \\ a+e+d&=q_i+p_j+m+n \\ b+e+c&=p_i+q_j+m+n \end{cases} \]

结合不难得到

\[\begin{cases} a=q_i+\frac{m}{2}\\ b=p_i+\frac{n}{2}\\ c=q_i+\frac{m}{2}\\ d=p_i+\frac{n}{2}\\ e=\frac{m+n}{2} \end{cases} \]

于是建图时将所有权值全部 \(\times2\)，计算答案时除回去即可。这样做看上去较为复杂，但套路化之后就不难了。

(2) 切糕模型

给出 \(n\) 个变量 \(x_i\)，其中每个变量的取值范围是\([1,m]\)。对于一个变量 \(x_i\)，取 \(j\) 的代价为 \(a_{i,j}\)。同时，给出若干限制条件 \((u,v,w)\)，表示 \(x_u-x_v\le w\) 或 \(x_u-x_v\ge w\)。

请求出一种合法的赋值方案，使得代价总和最小。

将每个变量 \(x_i\) 拆成 \(p_{i,1},p_{i,2}\cdots p_{i,m}\)，表示每个变量选 \([1,m]\) 的情况。对于每个变量建出一条链，\(S\rightarrow p_{i,1}\rightarrow p_{i,2}\rightarrow \cdots \rightarrow p_{i,m}\rightarrow T\)，相邻两点之间的流量是 \(a_{i,j}\)，连接源汇点的边流量为 \(\infty\)。那么断掉哪一条边，就表示该变量选择了哪个取值。

同时对于 \(x_u-x_v\ge w\)，连接边 \(p_{v,i}\rightarrow p_{u,i+w}\)，流量为 \(\infty\)。一般地，最小割中流量为 \(\infty\) 的边表示改变无法断开。具体到本题，表示若选择违背了限制，显然 \(S,T\) 仍然可以连通，无法产生最小割。

3. 最小割的推论

将跑完最大流的残量网络进行缩点，流量为 \(0\) 的边视为不连通，得到一个 DAG。现在分析这个 DAG 的性质。

\(S,T\) 必然不连通

如果 \(S,T\) 仍连通，原图上仍有增广路，并未跑满最大流。

对于满流边 \((u,v)\)，若 \(S,u\) 在同一 SCC， \(v,T\) 在同一 SCC，则 \((u,v)\) 必然在原图最小割上。

若 \((u,v)\) 的流量增加，原图重新连通，则最大流流量增加，最小割容量增加，因此 \((u,v)\) 必然出现在最小割中。

若 \((u,v)\) 不在同一 SCC，\((u,v)\) 可能在原图最小割中。

显然原图缩点之后得到的新图只有满流边，原图的任意一个割都是最小割，都可出现在最小割中。

4. 最小割树

求出网络上任意两点的最小割，如果暴力来求，复杂度是 \(O(V^4E)\) 的。采用最小割树可优化到 \(O(V^3E)\)。

下面介绍最小割树的构建方法。

选择任意两个点 \(u,v\)，求出最小割，并在新图中将 \(u,v\) 之间连接一条边权为最小割的边。
将整张图的节点分为两部分 \(U\) 集合和 \(V\) 集合，使得割后一部分与 \(u\) 联通，一部分与 \(v\) 联通。
分别递归调用与 \(u\) 联通的部分和与 \(v\) 联通的部分，即 \(U\) 集合和 \(V\) 集合。

于是任意两点的最小割，就是它们在最小割树上的简单路径的最小值。具体代码的实现上，将 \(U\) 集合放在序列的左端，\(V\) 集合放在序列的右端，由于最小割树的性质，对于 \(\forall a\in U,b\in V,c(a,b)=\min(c(a,u),c(u,v),c(v,b))\)。显然 \(c(a,u)\) 和 \(c(v,b)\) 在我们递归调用的过程中已知， \(c(u,v)\) 我们刚刚求得，于是将两点间最小割存储到数组中，复杂度为 \(O(V^3+Q)\)。

代码：

#include <iostream>
#include <queue>
#include <unordered_map>
#define N 855
#define M 17505
#define inf 1000000000
using namespace std;
unordered_map<int, int>mp;
int n, m;
struct Netflow {
	int s, t;
	struct Node {
		int to, nxt, val, fval;
	}e[M];
	int head[N], cnt = 1;
	void add(int u, int v, int w) {
		e[++cnt].to = v;
		e[cnt].fval = w;
		e[cnt].nxt = head[u];
		head[u] = cnt;
	} 
	void build() {
		scanf("%d%d", &n, &m);
		for (int i = 1; i <= m; i++) {
			int x, y, w;
			scanf("%d%d%d", &x, &y, &w);
			add(x, y, w);
			add(y, x, w);
		}
	}
	int cur[N], dep[N];
	int bfs() {
		for (int i = 1; i <= n; i++)
			dep[i] = inf;
		queue<int>q;		
		q.push(s);
		dep[s] = 0;
		cur[s] = head[s];
		while (!q.empty()) {
			int x = q.front();
			q.pop();
			for (int i = head[x]; i; i = e[i].nxt) {
				int y = e[i].to;
				if (e[i].val > 0 && dep[y] == inf) {
					q.push(y);
					dep[y] = dep[x] + 1;
					cur[y] = head[y];
					if (y == t)
						return 19260817;
				}
			} 
		}
		return 0;
	}
	int dfs(int x, int sum) {
		if (x == t)
			return sum;
		int k, flow = 0;
		for (int i = cur[x]; i && sum; i = e[i].nxt) {
			int y = e[i].to;
			if (e[i].val > 0 && dep[y] == dep[x] + 1) {
				k = dfs(y, min(e[i].val, sum));
				e[i].val -= k;
				e[i ^ 1].val -= k;
				sum -= k;
				flow += k; 
			}
		}
		return flow;
	}
	int dinic() {
		for (int i = 2; i <= cnt; i++)
			e[i].val = e[i].fval;
		int res = 0;
		while (bfs())
			res += dfs(s, inf);
		return res;
	}
} Nf;

struct GHT {
	int node[N], tmp[N];
	int cut[N][N];
	void solve(int l, int r) {
		if (l == r)
			return;
		Nf.s = node[l];
		Nf.t = node[r];
		int k = Nf.dinic(), s = node[l], t = node[r];
		cut[s][t] = cut[t][s] = k;
		int L = l, R = r;
		for (int i = l; i <= r; i++) {
			if (Nf.dep[node[i]] < inf)
				tmp[L++] = node[i];
			else
				tmp[R--] = node[i];
		}
		for (int i = l; i <= r; i++)
			node[i] = tmp[i];
		solve(l, L - 1);
		solve(L, r);
		for (int i = l; i < L; i++)
			for (int j = L; j <= r; j++) {
				cut[node[i]][node[j]] = cut[node[j]][node[i]] = min(min(cut[node[i]][s], cut[node[j]][t]), cut[s][t]);
				mp[cut[node[i]][node[j]]] = 1;
			}
	}
	void build() {
		for (int i = 1; i <= n; i++)
			node[i] = i, cut[i][i] = inf;
		solve(1, n);
		cout << mp.size() << "\n";
	}
} Ght;

int main() {
	Nf.build();
	Ght.build();
	return 0;
}

四、费用流

(1) 最小费用最大流

显然，一张网络的最大流不一定只有一个。若每条边的单位流量都有费用，考虑寻找一个流使得在流量最大的前提下费用最小。

考虑费用流中反向边的问题。撤回流量的同时费用要同时撤回，因此反向边的费用为正向边的相反数。

显然 对于费用和最小的增广路，我们想让它的流量最大，因此要尽早走。于是我们需要求最短路。考虑到有负边权，我们使用 SPFA。一般地，我们使用 EK 单源增广寻找增广路，因此我们通常使用 EK+SPFA 的费用流。复杂度为 \(O(V^2E^2)\)，但显然这只是上界。

注意求出一条流之后将所有边的流量恢复为原值。

代码：

int dis[N];
int inr[N];
int vis[N];
int pre[N];
int s, t;
int SPFA() {
	for (int i = 1; i <= n; i++) {
		dis[i] = inf;
		vis[i] = 0;
	}
	queue<int>q;
	q.push(s);
	dis[s] = 0;
	inr[s] = inf;
	vis[s] = 1;
	while (!q.empty()) {
		int x = q.front();
		q.pop();
		vis[x] = 0;
		for (int i = head[x]; i; i = e[i].nxt) {
			int y = e[i].to;
			if (e[i].flow > 0 && dis[x] + e[i].val < dis[y]) {
				dis[y] = dis[x] + e[i].val;
				inr[y] = min(inr[x], e[i].flow);
				pre[y] = i;
				if (!vis[y])
					vis[y] = 1, q.push(y);
			}
		}
	}
	return dis[t] < inf;
}
int maxflow, mincost;
void MCMF() {
	while (SPFA()) {
		mincost += dis[t] * inr[t];
		if (mincost > 0) {
			mincost -= dis[t] * inr[t];
			mincost = -mincost;
			maxflow += mincost / dis[t];
			return;
		}
		maxflow += inr[t];
		int i;
		for (int x = t; x != s; x = e[i ^ 1].to) {
			i = pre[x];
			e[i].flow -= inr[t];
			e[i ^ 1].flow += inr[t];
		}
	} 
}

(2) 费用流常见建模

其实费用流的建模没什么好讲的，掌握好最大流的建模套路其实就差不多了。

未完待续~~~

标签：增广,int,网络,笔记,最小,学习,dep,流量,rightarrow
From： https://www.cnblogs.com/Rock-N-Roll/p/18364972

网络流学习笔记

网络流学习笔记

一、定义

二、最大流问题

1. 最大流算法

(1) 增广路

(2) FF 算法

(3) 反向边与撤销影响

(4) EK 算法

(5) Dinic 算法

(6) Dinic 算法的优化

2. 最大流建模技巧

(1) 拆点

(2) 二分图

三、最小割问题

1. 最大流最小割定理

(1) 内容

(2) 证明

2. 最小割建模技巧

(1) 环式建模

a. 双环建模

b. 单环建模

(2) 切糕模型

3. 最小割的推论

4. 最小割树

四、费用流

(1) 最小费用最大流

(2) 费用流常见建模

相关文章

赞助商

阅读排行

网络流学习笔记

网络流学习笔记

一、定义

二、 最大流问题

1. 最大流算法

(1) 增广路

(2) FF 算法

(3) 反向边与撤销影响

(4) EK 算法

(5) Dinic 算法

(6) Dinic 算法的优化

2. 最大流建模技巧

(1) 拆点

(2) 二分图

三、最小割问题

1. 最大流最小割定理

(1) 内容

(2) 证明

2. 最小割建模技巧

(1) 环式建模

a. 双环建模

b. 单环建模

(2) 切糕模型

3. 最小割的推论

4. 最小割树

四、费用流

(1) 最小费用最大流

(2) 费用流常见建模

相关文章

赞助商

阅读排行

二、最大流问题