内心
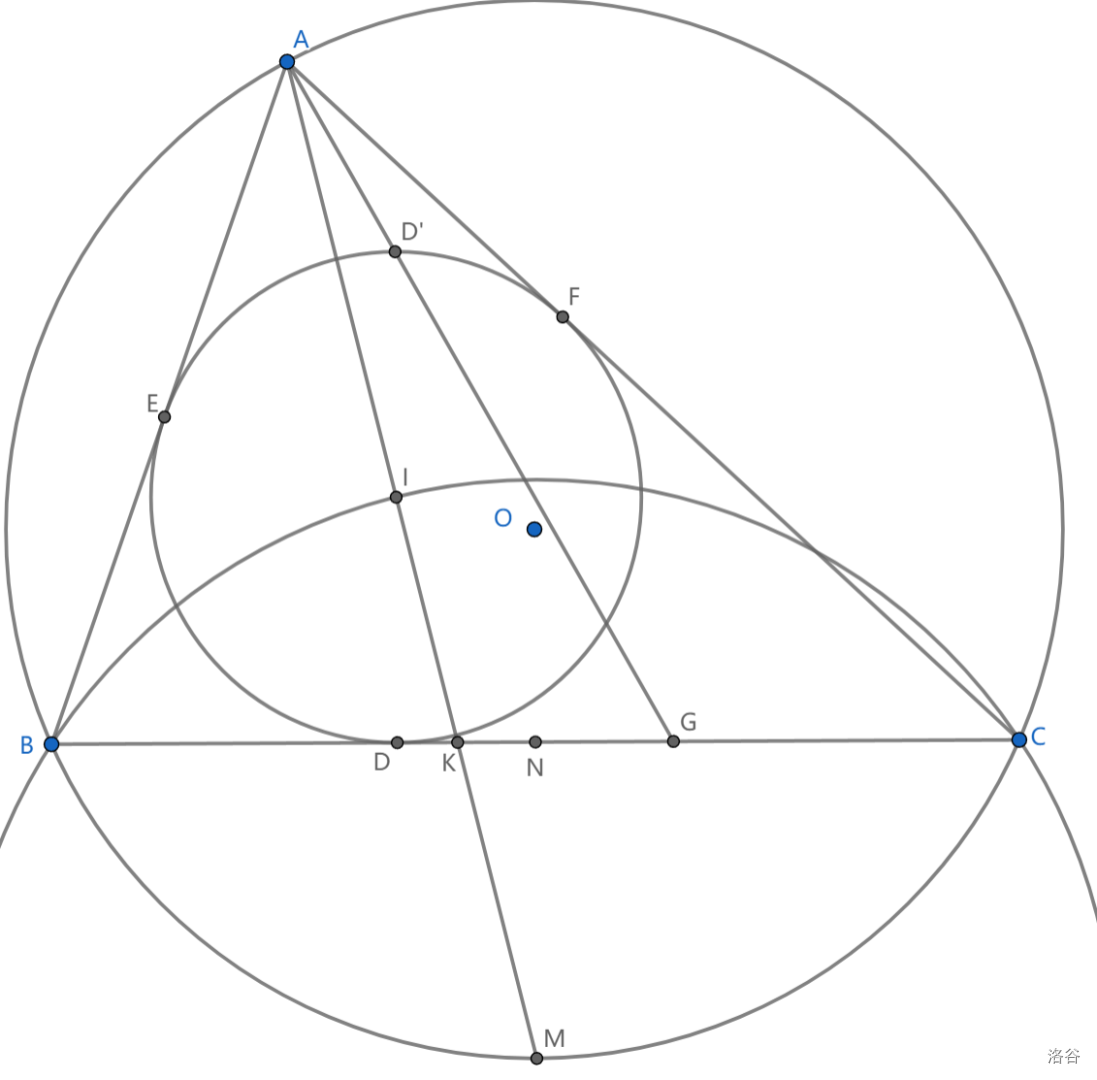
1、三条角平分线
2、在 \(\odot M\) 上(鸡爪圆上)
3、\(AI\cdot IM=AM\cdot IK=2Rr\) ,即 \(OI^2=R^2-2Rr\)
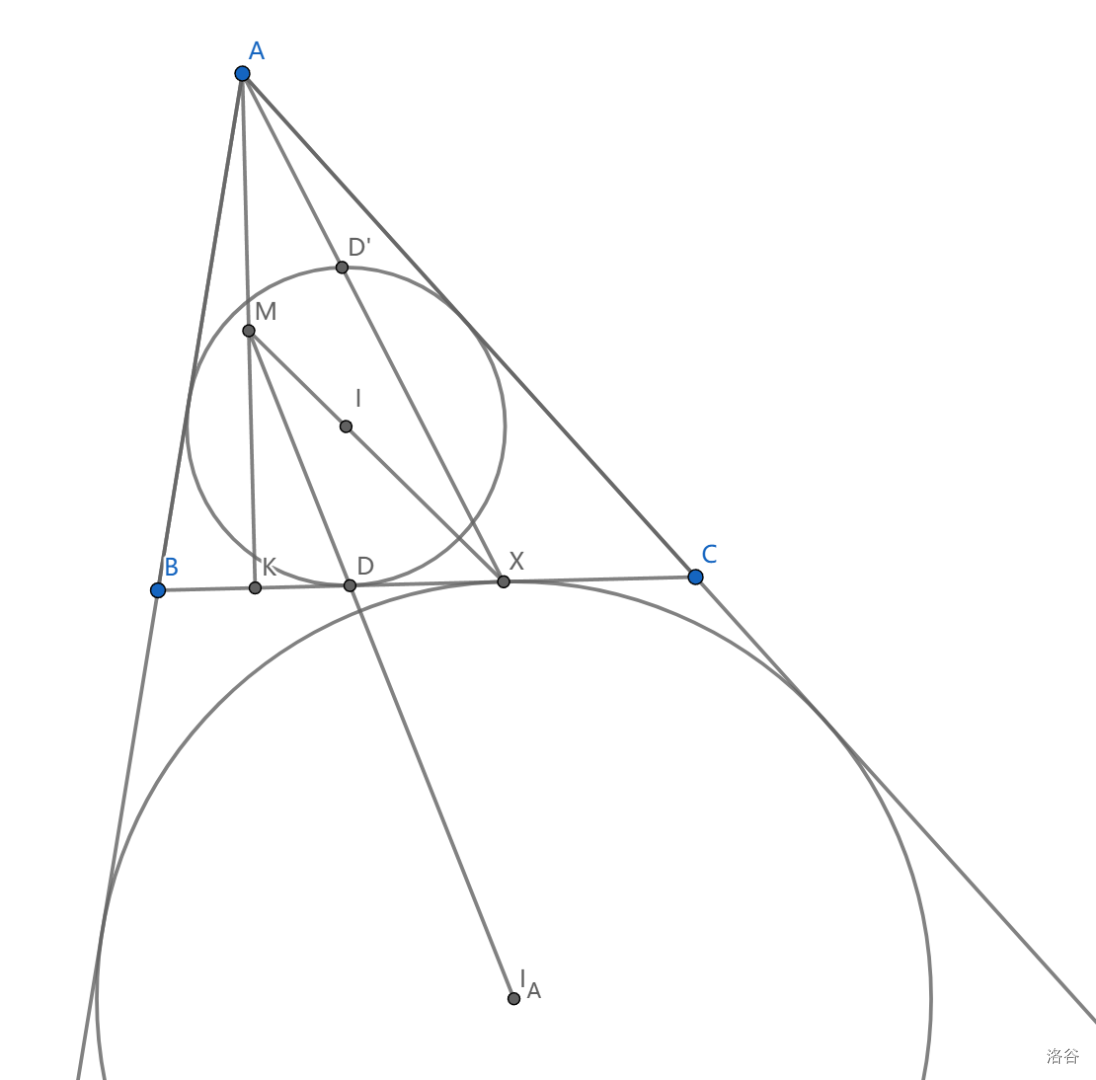
4、\(\odot I\) 与 \(\odot I_A\) 关于点 \(A\) 位似,所以 \(D\) 的对径点 \(D'\) 满足 \(AD'X\) 共线(两个圆过这两个点的切线平行),同理 \(AD\) 过 \(X\) 的对径点
必须要指出,关于 \(A\) 的位似还能给出鸡爪圆
5、设 \(N\) 是 \(BC\) 中点,则 \(IN//AX\) (利用中位线即可)
6、\(XI,I_AD\) 交于 \(AK\) 的中点
利用 \(\triangle XDE\) 与 \(\triangle XKA\) 位似,其中 \(I,M\) 都是中点,所以是位似对应点, \(XIM\) 共线, \(I_ADM\) 同理。
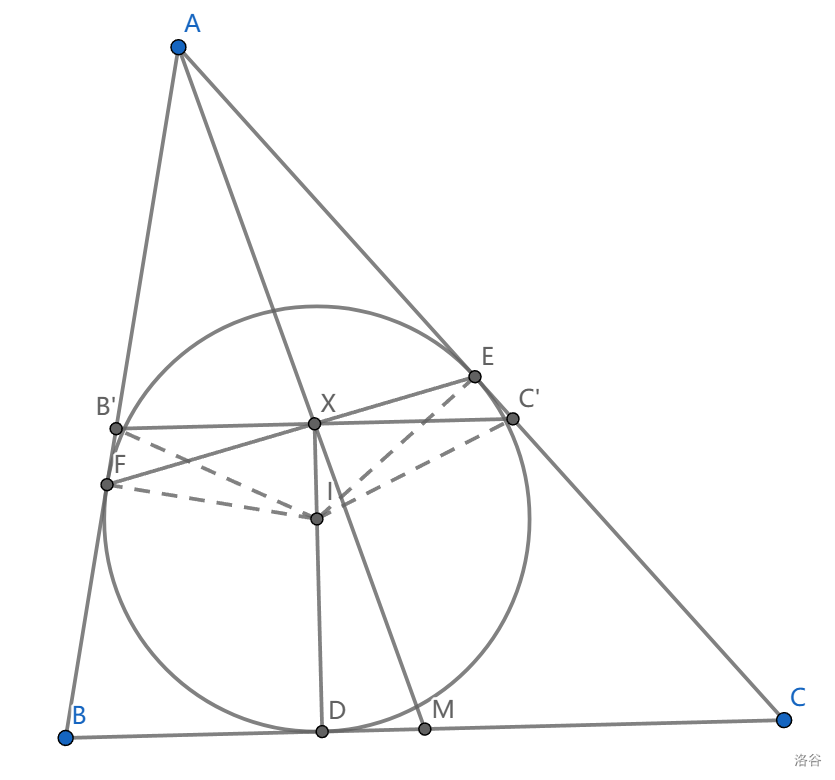
7、\(AM,ID,EF\) 共点
这个证明有点难度。我们要构造过 \(X=DI\cap EF\) 平行于 \(BC\) 的直线,假设它是 \(B'C'\) 。然后我们看到 \(B'FIX,C'EXI\) 共圆
所以 \(\angle FB'I=\angle FXI=\pi-\angle EXI=\angle IC'E\) ,说明 \(\triangle IB'F\cong \triangle IC'E\)
并且 \(\angle IB'X=\angle IFX=\angle IEX=\angle IC'X\) ,也就是 \(IB'=IC'\) ,而 \(\angle B'XI=Rt\angle\) ,所以 \(B'X=XC'\)
现在 \(X,M\) 是 \(\triangle AB'C',\triangle ABC\) 的相似对应点,所以 \(AXM\) 共线
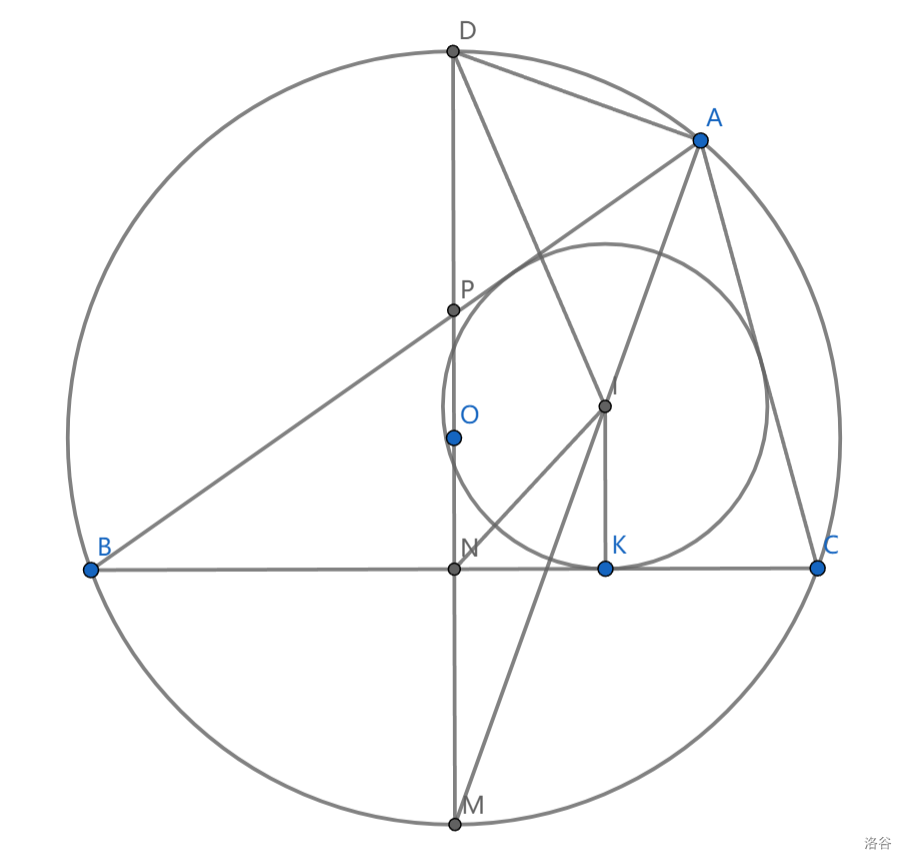
5、\(AI\) 为 \(\triangle DNI\) 外接圆的切线 (可用圆的弧中点性质证明)
6、\(\triangle INK \sim \triangle IDA\)
7、\(ND\) 中点 \(P\) 满足 \(PA=PK\)
8、取 \(\overset{\frown}{AB}\) 与 \(\overset{\frown}{AC}\) 的中点可构成平行四边形,且对角线垂直于 \(AI\)
9、\(\triangle MNI \sim \triangle MID\)
根据弧中点的性质和鸡爪定理 \(MN\cdot MD=MB^2=MI^2\)
例1
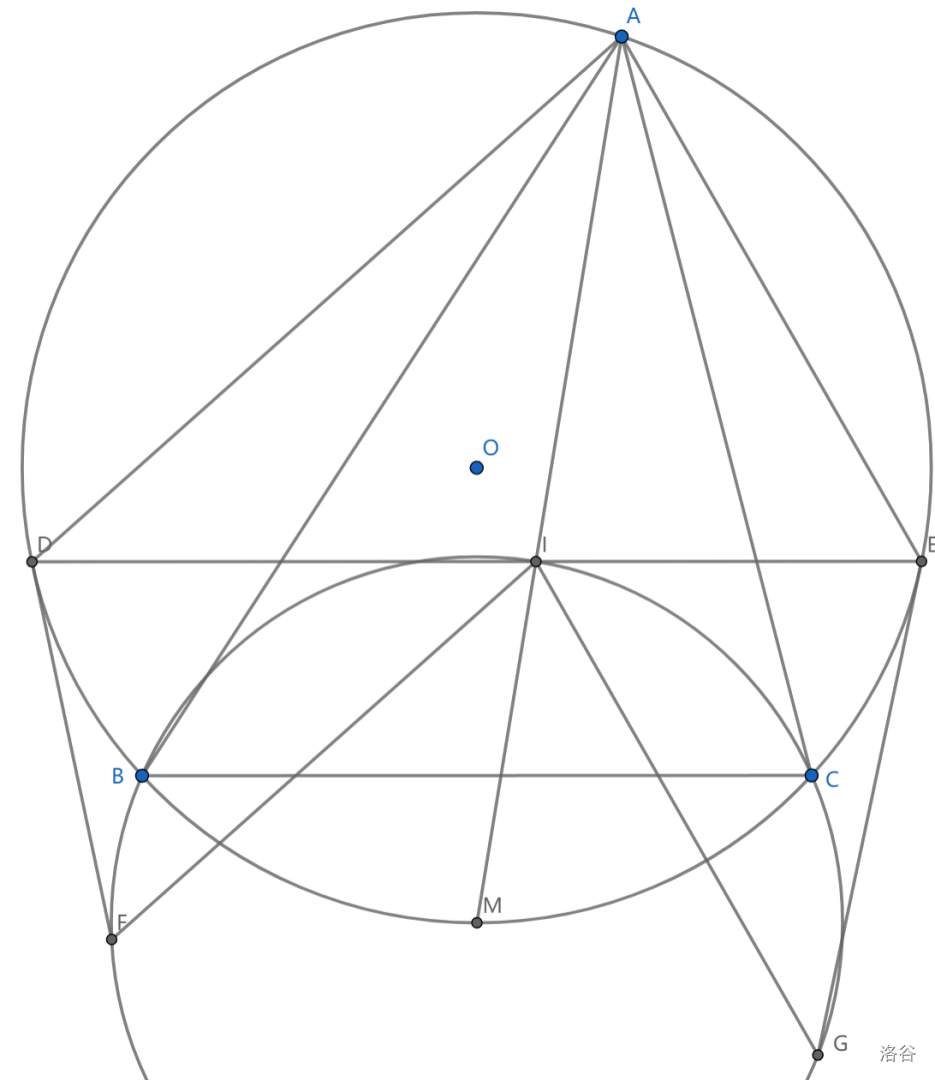
如图, \(I\) 为 \(\triangle ABC\) 内心,过 \(I\) 作 \(BC\) 平行线交外接圆 \(O\) 于 \(D,E\) ,过 \(D,E\) 作外接圆切线,分别与 \(IG // AE\) 交于 \(G\) , \(IF// AD\) 交于 \(F\) ,求证:\(B,C,F,G\) 共圆
先画出这个圆,就可以注意到 \(I\) 也在这个圆上,即该圆为鸡爪圆
不难注意到本题中的 \(IF//AD\) 构成了 \(Reim\) 引理(平行+共圆=共圆!)的模型(\(DF\) 为切线)
从而 \(IMFD\) 共圆,接下来知道了是鸡爪圆,我们就会考虑处理点 \(M\)
实际上 \(\angle MFI=\angle MDI=\angle MDF=\angle MIF\) ,从而 \(MF=MI\)
同理可证 \(MG=MI\) ,这就证毕。
例2
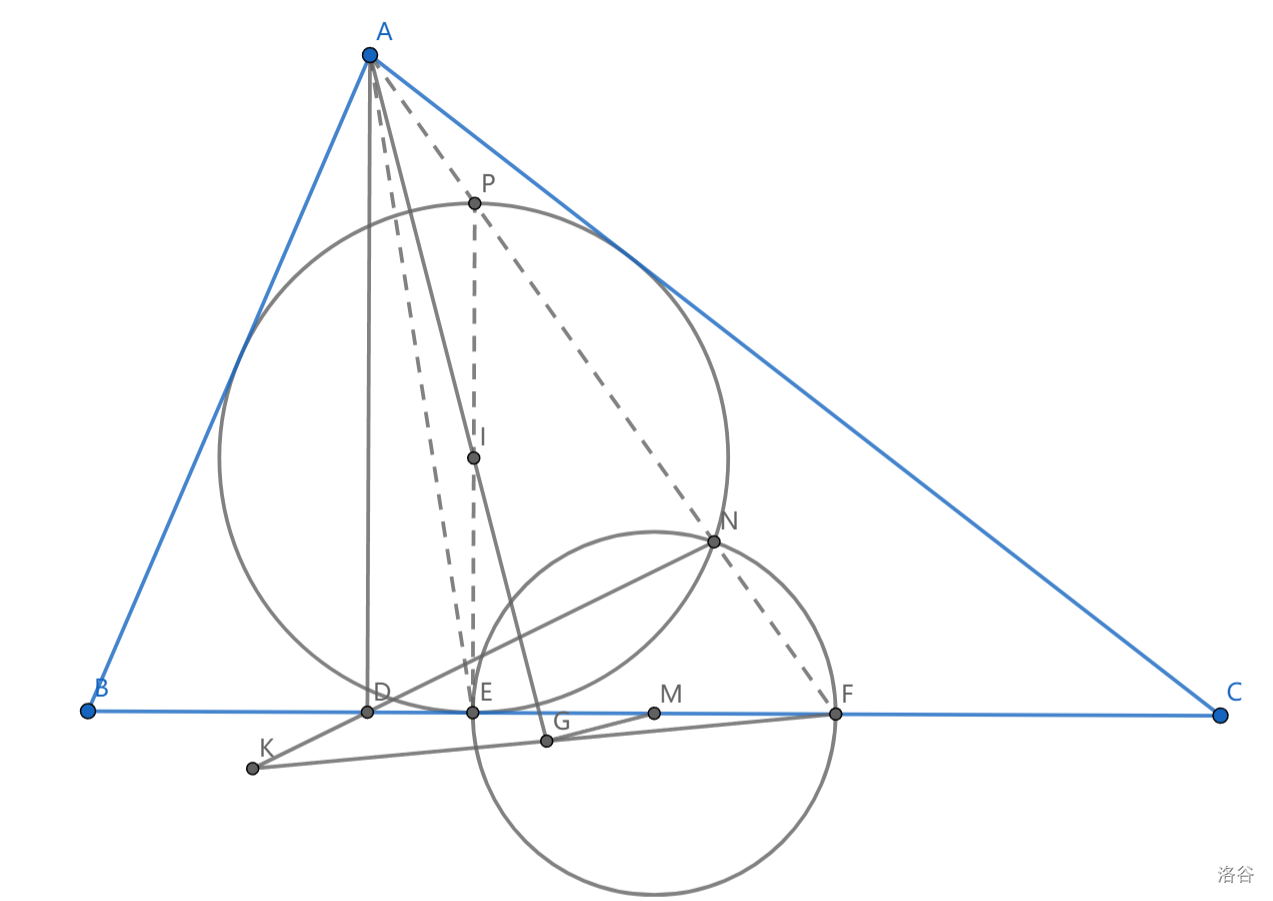
如图,\(AD\perp BC\) 于点 \(D\) , \(\triangle ABC\) 内切圆 \(I\) 切 \(BC\) 于点 \(F\) ,\(M\) 为 \(BC\) 中点,以 \(M\) 为圆心, \(ME\) 为半径画圆交圆 \(I\) 与 \(BC\) 于 \(N,F\) ,作 \(MG\perp AI\) 于点 \(G\) ,延长 \(FG,ND\) 交于点 \(K\) ,求证: \(D,E,K,G\) 共圆
分析:\(E,F\) 关于 \(M\) 对称,不难想到构造 \(E\) 的对径点,可以发现 \(A,P,N,F\) 共圆,这是因为 \(MI\) 垂直平分 \(EN\) 且为 \(PF\) 对应中位线
借助 \(ANED\) 共圆,由 \(FD\cdot FE=FN\cdot FA\) ,从而只需证 \(ANKG\) 共圆即可
那么只需证 \(\angle AND=\angle AGK\), 消点 \(K\) 并尽量转移,得到 \(\angle FGM(=)\angle DNE=\angle DAE=\angle APE\) ,可用 \(SAS\) 证明 \(\triangle PAE\sim \triangle MGF\) ,即证
也可用 \(IM//PF\) 和 \(Reim\) 引理得到 \(AEGF\) 共圆,然后导角
例3
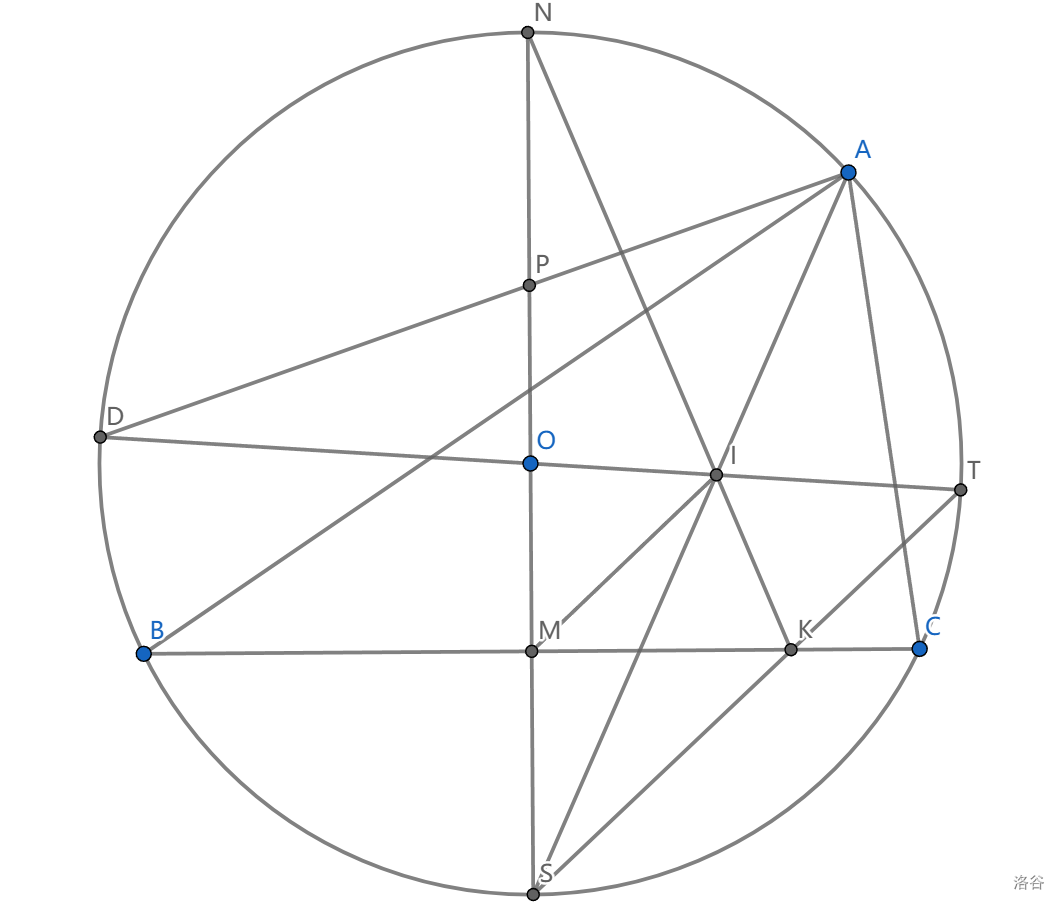
如图, \(O,I\) 分别为 \(\triangle ABC\) 的外心与内心, \(S\) 是弧 \(BC\) 的中点, \(N\) 是弧 \(BAC\) 的中点。延长 \(NI\) 与 \(BC\) 交于点 \(K\) ,直线 \(IO\) 与 \(\odot O\) 交于 \(D,T\) 两点, 已知 \(AD\) 平分线段 \(NI\) ,求证: \(S,K,T\) 共线。
可以用同一法做,会简单一些。
令 \(M=NS\bigcap BC,P=AD\bigcap NI\)
平分的条件如何利用?我们看到一个直角三角形, \(\angle NAS=Rt\angle => PN=PI=PA\)
根据性质 \(9\) , \(\triangle SMI \sim \triangle SIN\) ,有 \(\angle NIA=\pi -\angle NIS=\pi -\angle IMS\)
由于 \(NS,DT\) 为直径,有 \(\angle PAI=\angle DAS=\angle NST\)
又 \(PA=PI=>\angle PAI=\angle PIA\)
有 \(\angle PIA=\angle NST\)
即 \(\angle MST+\angle IMS=\pi\)
即 \(ST//MI\)
而 \(MI//SK\iff \frac{MS}{NS}=\frac{IK}{NK} \iff R^2-OI^2=2Rr\) 成立
即证。