标签：limits 题解 sum cap leq ABC366D left

Solution

题意简述

给你一个正整数 \(N\) 和 \(N^3\) 个非负整数，表示为 \(A_{x,y,z}\) 其中 \(1 \leq x, y, z \leq N\) 。

您将得到以下格式的 \(Q\) 个查询，必须按顺序处理。

对于第 \(i\) 次查询 \((1 \leq i \leq Q)\) ，您将得到一个整数元组 \((Lx_i, Rx_i, Ly_i, Ry_i, Lz_i, Rz_i)\) ，其中 \(1 \leq Lx_i \leq Rx_i \leq N\) , \(1 \leq Ly_i \leq Ry_i \leq N\) , 和 \(1 \leq Lz_i \leq Rz_i \leq N\) 。求

\[\sum\limits_{x=Lx_i}^{Rx_i} \sum\limits_{y=Ly_i}^{Ry_i} \sum\limits_{z=Lz_i}^{Rz_i} A_{x,y,z} \]

题解

简单三维前缀和。考虑一下容斥关系就好了。

code

容斥知识补充

既然题解写都写了，写详细一点。

首先引入容斥的最经典的就是这张韦恩图（来自 OI-wiki）：

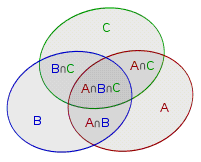
现在我想知道 \(|A\cup B\cup C|\)，并不是简单粗暴的三个集合大小相加，因为互相有重叠部分。正确答案是：\(|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|\)。相信还是很好理解的这里不赘述了。

把它推广到一般情况，就是我们熟悉的容斥原理了。

定义

\[\left|\bigcup_{i=1}^nS_i\right|=\sum\limits_i\left|S_i\right|-\sum\limits_{i<j}\left|S_i\cap S_j\right|+\sum\limits_{i<j<k}\left|S_i\cap S_j\cap S_k\right|-\dots\\ +(-1)^{m-1}\sum\limits_{a_i<a_{i+1}}\left|\bigcap_{i=1}^mS_{a_i}\right|+\dots+(-1)^{n-1}\left|S_1\cap\dots\cap S_n\right| \]

整理，得

\[\left|\bigcup_{i=1}^nS_i\right|=\sum\limits_{m=1}^n(-1)^{m-1}\sum\limits_{a_i<a_{i+1}}\left|\bigcap_{i=1}^mS_{a_i}\right| \]

证明

我们计算每个元素出现的次数，对于 \(x\)，假设它出现在 \(T_1,\dots,T_m\) 的集合中。

\[\begin{aligned} Cnt&=|\{T_i\}|+\dots+(-1)^{k-1}\left|\left\{\bigcap_{i=1}^kT_{a_i}|a_i<a_{i+1}\right\}\right|+\dots+(-1)^{m-1}|\{T_1\cap\dots\cap T_m\}|\\ &=\binom{m}{1}-\binom{m}{2}+\dots+(-1)^{m-1}\binom{m}{m}\\ &=\binom{m}{0}-\sum\limits_{i=0}^m(-1)^i\binom{m}{i}\\ &=1-(1-1)^m=1 \end{aligned} \]

每个元素出现次数为 \(1\)，合并起来就是并集了，证毕。

标签：limits,题解,sum,cap,leq,ABC366D,left
From： https://www.cnblogs.com/WerChange/p/18354670