CF1674G
给出一个 \(n\) 点 \(m\) 边的有向无环图,你需要从中移除一些边,使得对于每一个点,其入度减少(如果原来有入边),出度也减少(如果原来有出边)。
当删完边以后,如果有一个点集,满足对于任两点 \((i,j)\) 可以从 \(i\) 走到 \(j\) 或可以从 \(j\) 走到 \(i\),那就称其为可爱的。
现在要构造一种删边方案,使得删边后其中一个可爱的点集最大,输出这个点集大小。
\(1 \leq n \leq 2 \cdot 10^5, 0 \leq m \leq 2 \cdot 10^5\)
-
这题无论对于删边操作和可爱的点集操作咋一看都完全没有思路
-
当没有思路的时候,考虑把原问题转化成数学语言解释
-
发现可爱的点集在强连通分量缩点后一定是一条链
-
但这个性质不太好看,咋一看还是毫无思路
-
为了让他更好看,我们可以发现,那些被我们缩的点考虑更严格的限制住他
-
换言之,我们考虑直接把要缩的点拆成一条链,则一个可爱的点集就可以直接描述成一条链
-
感性的猜测结束,我们来理性证明一下一个可爱的点集是一条链是一个充要条件
-
必要性:
- 非常显然,对于点集中的两点 \(u,v\),顺着链走一定满足条件
-
充分性:
-
考虑把原图中任两点 \(u,v\) 满足可以从 \(u,v\) 的在新图上连一条有向边 \((u,v)\),则这张图变成一张竞赛图,我们只需要证明这张竞赛图可以有一种方法划分出一条哈密顿路径即可
-
实际上这是一个比较重要的结论,与之同等重要的结论是强连通的竞赛图一定有一种方法划分出一条哈密顿回路
-
具体证明的话,可以考虑从这张竞赛图的某个入度为 \(0\) 的点跑出一棵 \(dfs\) 树,按便利顺序给根节点的所有儿子按续编号,可以注意到从编号高的子树中一定有横插边连入编号低的子树。为了方便考虑,我们先考虑只有两个儿子的情况
-
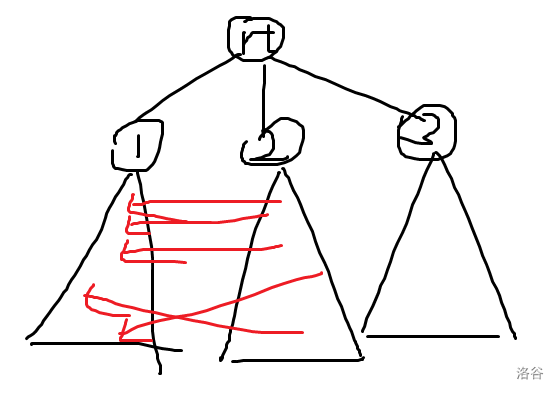
-
因为原图是竞赛图,这两个儿子中的每个节点都有从 \(2\) 到 \(1\) 的横插边相连,也就是说,我们交换 \(dfs\) 顺序,从第 \(2\) 个儿子先便利,一定可以把第 \(1\) 个儿子消掉
-
考虑重复这一操作,我们从第 \(3,4,\cdots,k\) 个儿子一次便利,每次都可以消去前一个儿子,最终就只会把根节点削成只有一个儿子
-
因此,我们可以递归到这一个儿子,重复上述过程,最终可以把整张竞赛图缩成一条链
-
我们按照这张图中链的连接方式在原图中连接点集中节点,得到的点集一定是可爱的
-
拓展
-
虽然证明强连通竞赛图有哈密顿回路和这题没有一点关系,但还是在这里拓展一一下
-
我们在竞赛图有哈密顿路径的基础上抽出这条链,按从左向右的方向拜访链路这上面一定存在很多除链路外向前向后的道路
-
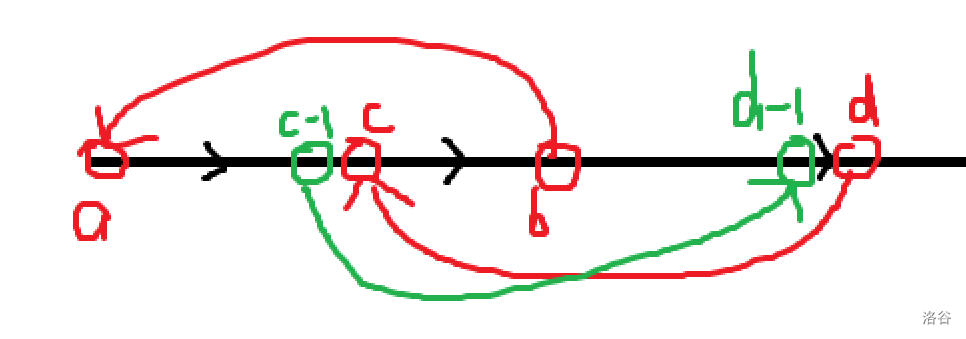
-
如图,我们找到从后面连向第一个点的一条边 \((b,a)\),因为原图是强连通的,一定可以找到这样一条边。同理,我们找 \(b\) 后一点 \(c\) 是的他是第一个在 \((a,b)\) 之间有一个 \(c\) 有连边 \((d,c)\) 的
-
因为 \(d\) 是第一个有向前连边的,所以 \(d-1\) 一定是向后连边的,我们取 \((c-1,d-1)\) 这条边
-
那么我们就可以注意到我们连成了 \(d \to c \to b \to a \to c-1 \to d-1 \to d\) 这条道路
-
同样的构造可以在之间穿插,最终构成了一个哈密顿回路
-
-
-
接下来我们考虑这条链需要满足什么条件,容易发现:
-
如果链上的中间某一个点入度为 \(1\) 或者出度为 \(1\),则不合法
-
如果链头的出度为 \(1\) 或者链尾的入度为 \(1\),则不合法。
-
-
转化为一个多源最长路的模型 \((DAG)\),可以扫一遍 \(dp\) 线性求解
-
最终复杂度 \(O(n)\)