笛卡尔树
1.权值 \(\text{pos}\) 满足二叉搜索树的性质,通常用序列的下标作为权值;
2.权值 \(\text{val}\) 满足二叉堆的性质。
实现方法
我们考虑将元素按照键值 \(k\) 排序。然后一个一个插入到当前的笛卡尔树中。那么每次我们插入的元素必然在这个树的右链(右链:即从根结点一直往右子树走,经过的结点形成的链)的末端。于是我们执行这样一个过程,从下往上比较右链结点与当前结点 \(u\) 的 \(w\),如果找到了一个右链上的结点 \(x\) 满足 \(x_w<u_w\),就把 \(u\) 接到 \(x\) 的右儿子上,而 \(x\) 原本的右子树就变成 \(u\) 的左子树。
具体如图所示,图中红框部分就是我们始终维护的右链:
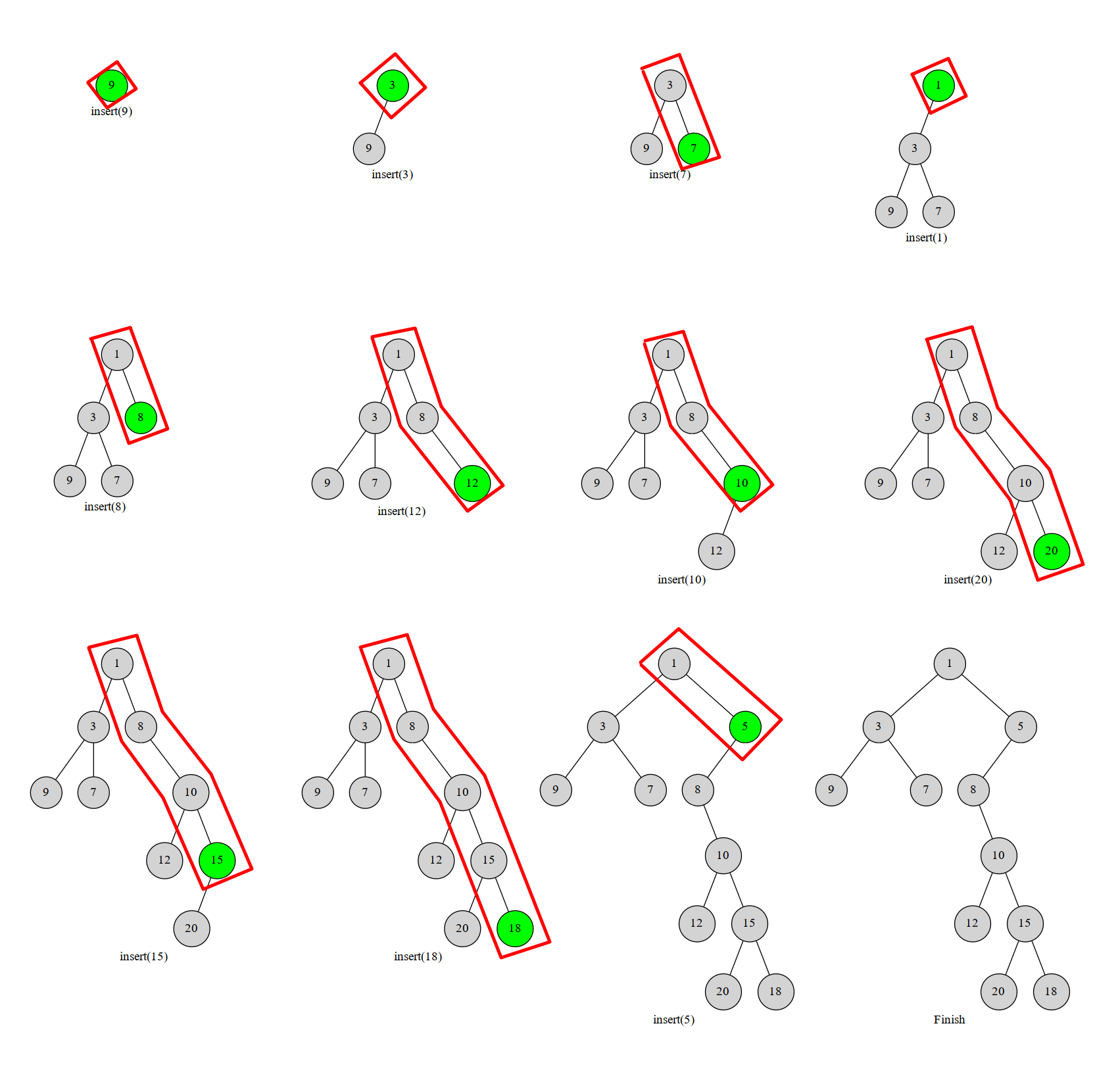
显然每个数最多进出右链一次(或者说每个点在右链中存在的是一段连续的时间)。这个过程我们可以用栈维护,栈中维护当前笛卡尔树的右链上的结点。一个点不在右链上了就把它弹掉。这样每个点最多进出一次,复杂度 \(O(n)\)。
典型例题
P5854 笛卡尔树
笛卡尔树模板题。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e7+5;
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(!isdigit(ch))
{
if(ch=='-')f=-1;
ch=getchar();
}
while(isdigit(ch))
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*f;
}
struct node
{
int l,r,pos,val;
}e[MAXN];
int n;
int s[MAXN],top;
int main()
{
n=read();
for(register int i=1;i<=n;i++)
{
e[i].val=read();
e[i].l=e[i].r=0;
e[i].pos=i;
}
for(register int i=1;i<=n;i++)
{
int k=top;
while(k>0&&e[s[k]].val>e[i].val)k--;
if(k)e[s[k]].r=i;
if(k<top)e[i].l=s[k+1];
s[++k]=i;
top=k;
}
long long ans1=0,ans2=0;
for(register int i=1;i<=n;i++)
{
ans1^=(long long)i*(e[i].l+1);
ans2^=(long long)i*(e[i].r+1);
}
printf("%lld %lld",ans1,ans2);
return 0;
}