思路分析
分析样例:
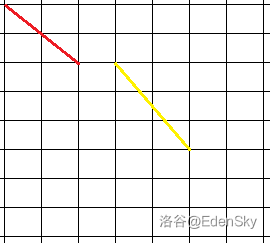
见红线,长宽各为 2,存在格点;黄线长 2 宽 3,没有格点。
考虑延长黄线使得长 4 宽 6,发现有格点。思考格点,如果长和宽都可以被分成 \(p\times l\) 的格式,则存在格点。那么,就能想出:
推论 1:对于 \((0 \ , \ 0)\) 和 \((x \ , \ y)\) 之间没有格点,当且仅当 \(\gcd(x \ , \ y )=1\)。
对推论 1 的证明:
若存在格点 \(A\),其坐标为 \((a \ , \ b)\),由于在同一直线上,斜率 \(k\) 相同,则有 \(k=\dfrac{a}{b}=\dfrac{x}{y}\),即 \(b=\dfrac{a\times y}{x}\)。由于 \(b\) 为整数,则有 \(x \ | \ a\times y\)。
采用反证法,\(\gcd(x \ , \ y )=1\) 时存在格点。
由于互质,\(x=\prod\limits_{i=1}^{s1}p_i^{c_i} \ , \ y=\prod\limits_{i=1}^{s2}q_i^{d_i}\),假设 \(x \ | \ y\),\(y\) 必然有因子 \(\prod\limits_{i=1}^{s1}p_i^{c_i}\),而实际上没有,所以 \(y\) 对该式没有贡献。即:$x \ | \ a\times y \Leftrightarrow x \ | \ a $。
而 \(A\) 是线段上一点,有 \(a<x\),则 \(b\) 一定不属于 \(\mathbb{Z^+}\),与原有条件冲突,由此可证。
得出推论 1 后,我们就能判断两点之间是否有格点了。那么如何得出最短答案呢?
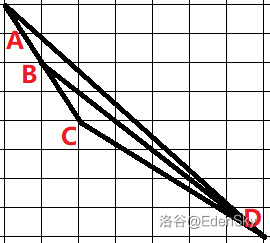
(图是随手画的,具体有的性质以下文所述为准。)
见上,假设 \(AD\) 之间存在格点(在之后称为不合法),于是我们找到任意一点 \(C\) 进行更新。
假设 \(C\) 为不合法,以图为例,在 \(AC\) 上可以取一格点 \(B\),根据三角形定则 \(| \ BD \ |>| \ BC \ |+| \ CD \ |\),则 \(B\) 更优。假设无法在 \(AB\) 和 \(BD\) 上取格点,那么 \(B\) 的取点是合法的,可以得出:
推论 2:对于任意不合法的取点,必然可以在原线段取到更优的合法方案。
那么就有:
推论 2.1:最优方案必然是合法的。
对推论 2.1 的证明:
假设最优方案不合法,根据推论 2,则有更优方案可以更新,与原有条件冲突,由此可得。
以上是一个转折点的情况,那如果有多个转折点呢?
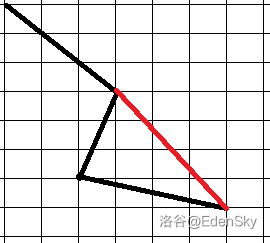
如图,多个转折点的情况是不需要考虑的,见图,由于三角形定则,红色线的长度小于另外两条边之和。换句话说:
推论 3:最优方案只转折一次或零次。
于是我们只要枚举一个点就可以了,如果在整个 \(n\times m\) 的范围枚举,寻找最优方案,但这个时间复杂度显然是不合理的。其实我们只需要枚举线段附近的点就可以,这样复杂度就可以变成 \(\mathcal{O}(n)\)。
代码实现
#define by_wanguan
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
int t,n,m,y11,y2,y3,g; double dn,dm,nowm,ans,k;
double dis(double a,double b,double x,double y){
return sqrt((x-a)*(x-a)+(y-b)*(y-b));
}
void solve(){
k=(double)m/n;//斜率
if((g=__gcd(n,m))==1)
{printf("%.15lf\n",dis(0,0,n,m)); return ;}
dn=n,dm=m;
for(int i=1;i<n;i++){
nowm=k*i;
y11=(int)(nowm),y2=y11+1,y3=y11-1;//x坐标为i时附近的点的y坐标
if(__gcd(n-i,m-y11)==1&&__gcd(i,y11)==1&&abs(y11-k*i)>1e-10)
//判断是否合法,abs()是在判断是否为原线段上的点
ans=min(ans,dis(i,y11,n,m)+dis(0,0,i,y11));
if(__gcd(n-i,m-y2)==1&&__gcd(i,y2)==1&&abs(y2-k*i)>1e-10)
ans=min(ans,dis(i,y2,n,m)+dis(0,0,i,y2));
if(__gcd(n-i,m-y3)==1&&__gcd(i,y3)==1&&abs(y3-k*i)>1e-10)
ans=min(ans,dis(i,y3,n,m)+dis(0,0,i,y3));
}
printf("%.15lf\n",ans);
}
int main(){
scanf("%d",&t); while(t--){
scanf("%d%d",&n,&m);
ans=1e9;
solve();
}
}