4.一次函数

4.1 函数的认识

函数的定义：

一般地，如果在一个变化过程中有两个变量 $x$ 和 $y$ ，并且对于变量 $x$ 的每一个值，变量 $y$ 者都有唯一的值与它对应，那么我们称 $y$ 是 $x$ 的函数，其中 $x$ 是自变量 .
表示函数的方法：

事实上，表示函数的方法与我们上学期学的表示变量间的关系大致相同。一般有：列表法，关系式法和图像法。
判断关系式或图像是不是函数关系或函数图像：
- 例题：判断下列关系式是不是函数关系：
  $(1).$ $y=2x$ , $y=x^2$ , $y=\sqrt x$ , $y=\sqrt [3]{x}$ ;
  $(2).$ $y^2=x$ , $y=\pm\sqrt x$ ;
显然，第一组的关系式都是函数关系，而第二组却相反。拿 $y=\pm\sqrt x$ 来说，对于变量 $x$ 的每一个值，变量 $y$ 者都有两个值与它对应，所以在这个关系式中， $y$ 并不是 $x$ 的函数。
- 例题：判断下列图像是不是函数图像；
  
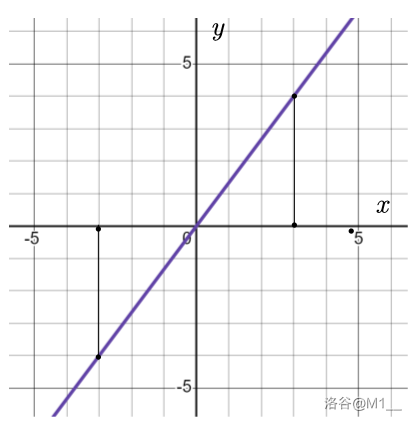
  我们做一条铅垂线，得出对于变量 $x$ 的每一个值，变量 $y$ 者都有唯一的值与之相对应，所以这个图像是函数图像。
再看这张图：

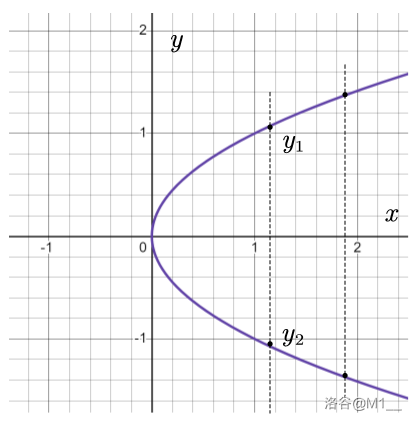
对于变量 $x$ 的每一个值，变量 $y$ 者都有两个值与它对应，所以在这个图像中， $y$ 并不是 $x$ 的函数。

4.2 番外篇：平面直角坐标系

同一平面内，画出两条具有公共原点的数轴并使他们相互垂直，就是平面直角坐标系。如图 $2-1$ ，其中水平的数轴叫做横轴，而另一条垂直的数轴则称之为纵轴。横轴和纵轴上的坐标分别称为横坐标和纵坐标。

平面直角坐标系中的点用数对表示。写作 $(a,b)$ , 其中第一个数是横坐标上的数。如横坐标为 $2$ ，纵坐标为 $3$ 的坐标表示为 $(2,3)$ .

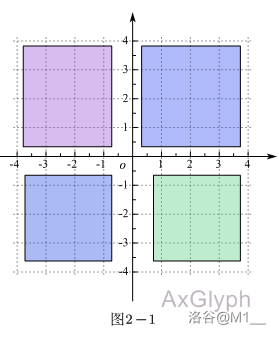
我们会发现，这两条数轴把整个坐标系分成了四个部分，我们把它称之为象限。如图 $2-2$ ：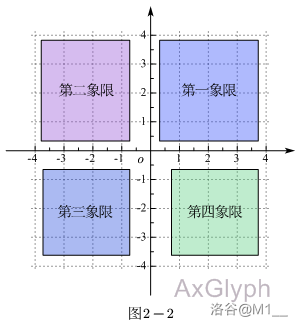
横轴或纵轴坐标特点以及各个象限坐标特点：
横轴上的坐标特点：即纵坐标为 $0$ ，写作 $(x,0)$ ;
纵轴上的坐标特点：即横坐标为 $0$ ，写作 $(0,y)$ ;
各个象限坐标特点如图 $2-3$ ：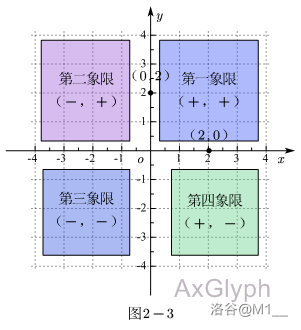

4.3 一次函数和正比例函数

一次函数和正比例函数的定义：

形如 $y=kx+b$ $(k\neq 0)$ 其中 $b$ 为任意实数，即 $x$ 的次数为 $1$ 且 $x$ 的系数不为 $0$ 。这时我们称 $y$ 是 $x$ 的一次函数。
当 $b=0$ 时，称 $y$ 是 $x$ 的正比例函数。

因此函数，一次函数，正比例函数的关系如图所示：
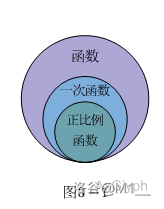
- 例题：已知 $x$ 是 $y$ 的一次函数， $y=(k-1)x^{k+2}+5$ ，求 $k$ 的值。
  $\therefore y$ 是 $x$ 的一次函数，
  $\because \left\{\begin{matrix} k+2=1 \\ k-1\neq 0 \\ \end{matrix}\right. \ 解得k=-1$ ;
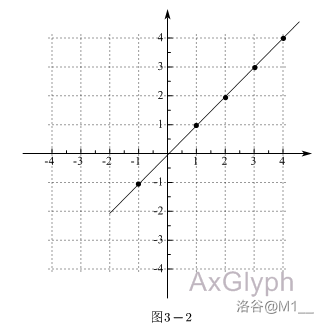
利用坐标系画一次函数，如 $y=x$ ;

1.列出表格，注意自变量在上。

$x$	$-1$	$0$	$1$	$2$	$3$	$4$	...
$y$	$-1$	$0$	$1$	$2$	$3$	$4$	...

2.根据表格中的数据确定坐标
3.连接即可。

4.4 一次函数的图像

4.4.1 正比例函数的图像

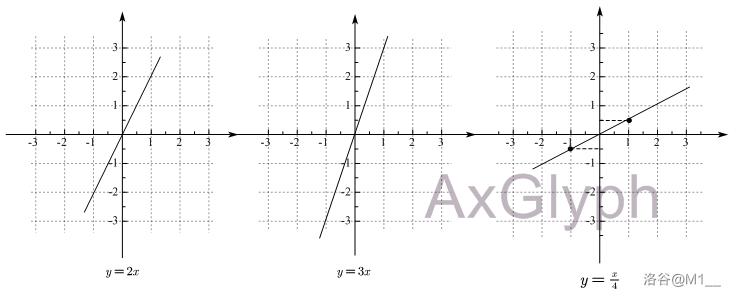
观察上图函数图象的特点，得出正比例函数 $y=kx+b\ (k \neq 0)$ 的函数图象是一条过原点的直线。
也就是说，只需描两个点 $(0,0),(1,k)$ 就可以画出正比例函数。
函数的增减性：
$y$ 随 $x$ 的增大而增大，（随 $x$ 的减小而减小），称 $y$ 为递增函数。
反之，$y$ 随 $x$ 的增大而减小，（随 $x$ 的减小而增大），称 $y$ 为递减函数。
判断一个函数增减性的方法：
- 具体求值法：
  若 $x_1>x_2$ , 则 $y_1>y_2$ , $y$ 是递增函数。
  若 $x_1<x_2$ , 则 $y_1<y_2$, $y$ 是递增函数。
  若 $x_1>x_2$ , 则 $y_1<y_2$ , $y$ 是递减函数。
  若 $x_1<x_2$ , 则 $y_1>y_2$, $y$ 是递减函数。
- 例如: 判断 $y=3x$ 的增减性；
  当 $x_1=1$ 时， $y_1=3$ ;
  当 $x_2=2$ 时， $y_2=3 \times 2=6$ ;
  $\therefore1<2,3<6 $ ,
  $\because y=3x$ 是递增函数。
- 观察函数图像的变化趋势
  
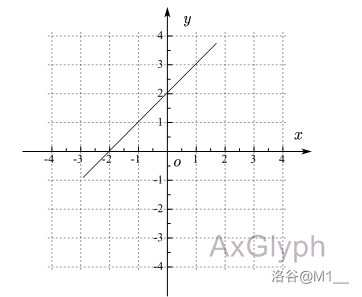
  据图可知， $y$ 随 $x$ 的增大而增大，（随 $x$ 的减小而减小），所以 $y$ 为递增函数。
- 正比例函数 $k$ 的正负性判定增减性：
  
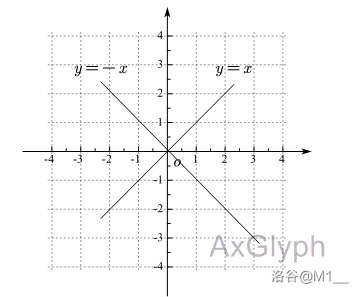
  根据上图我们可以发现，正比例函数 $y=kx\ (k\neq 0)$ 的函数增减性由 $k$ 的正负性决定。
  当 $k>0$ 时， $y$ 递增；
  当 $k<0$ 时， $y$ 递减。
函数的象限性：

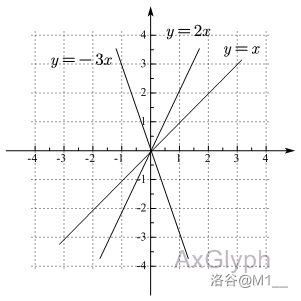
根据上图我们可以发现，正比例函数 $y=kx\ (k \neq 0)$ 的函数图像与 $k$ 的正负性有关。
- 当 $k>0$ 时，函数图像经过一，三象限；
- 当 $k<0$ 时，函数图像经过二，四象限；
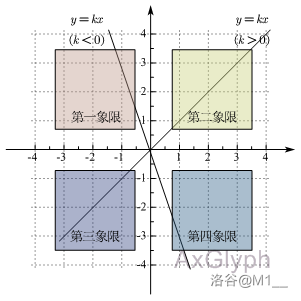
函数的倾斜度

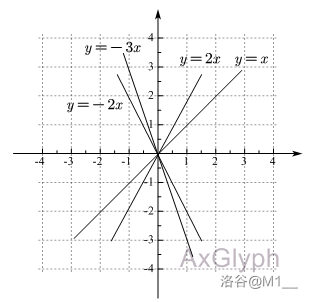
根据上图我们可以发现，正比例函数 $y=kx\ (k \neq 0)$ 的函数图像与 $|k|$ 有关。
$|k|$ 越大，函数图像越陡，函数图像越靠近 $y$ 轴， $y$ 随 $x$ 的变化速度越快。

4.4.2 一次函数的图像

一次函数的特点

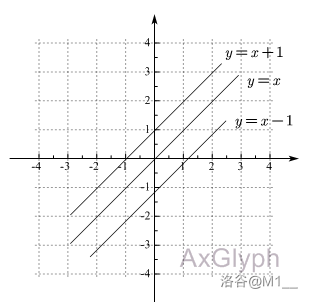
如图，在 $y=kx+b\ (k \neq 0)$ 中可得结论：
- 当 $b=0$ 时， $y=kx+b\ (k \neq 0)$ 时正比例函数；
- 当 $b>0$ 时，一次函数 $y=kx+b\ (k \neq 0)$ 的图像是由正比例函数 $y=kx\ (k \neq 0)$ 的图像向上平移 $b$ 个单位得到的。
- 当 $b<0$ 时，一次函数 $y=kx+b\ (k \neq 0)$ 的图像是由正比例函数 $y=kx\ (k \neq 0)$ 的图像向下平移 $b$ 个单位得到的。
一次函数的增减性
同理，一次函数 $y=kx+b\ (k \neq 0)$ 的增减性与 $k$ 的正负性有关。
当 $k>0$ 时，$y$ 递增；当 $k<0$ 时，$y$ 递减；
一次函数的象限性

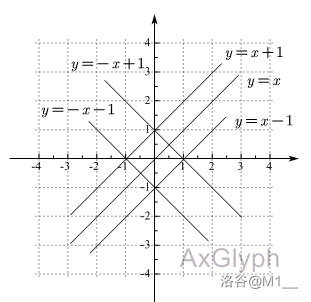
如图可知，一次函数 $y=kx+b\ (k \neq 0)$ 的象限性由 $k,b$ 的正负性共同决定。因此便有四种情况；
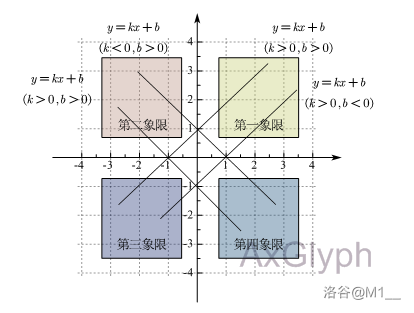
一次函数的倾斜度：
同理，一次函数 $y=kx+b\ (k \neq 0)$ 的倾斜度与 $|k|$ 的绝对值大小有关。
$|k|$ 越大，函数图像越靠近 $y$ 轴，函数图像越陡， $y$ 随 $x$ 的变化速度越快。
一次函数图像的平行条件

当 $y_1=k_1x+b_1\ (k_1 \neq 0)$ ;
$y_2=k_2x+b_2\ (k_2 \neq 0) $且 $k_1=k_2$ 时，两个函数图像互相平行。
一次函数图像的平移规律：
- 上下平移：
  即得到直线 $y=kx+b\ (k \neq 0)$ 向上平移 $n (n> 0)$ 个单位长度得到直线 $y=kx+b+n$ ，向下平移 $n (n>0)$ 个单位长度得到直线 $y=kx+b-n$ .
  因为上文涉及过，所以此处不再赘述。
- 左右平移：
  这个理解起来似乎有点反人类，具体如下：
  拿最简单的函数图像 $y=x$ 来讲，如下图，将直线向左平移 $1$ 个单位长度；
  
  在七年级上册，我们就已经学过点动成线，线动成面，面动成体的思想。所以直线的平移就可以看成直线上所有点的平移。
  
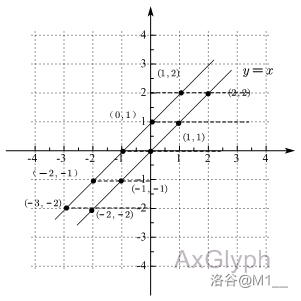
  结合上述语句和图像上标出的坐标来看，当函数图像整体向左平移 $1$ 个单位长度时，平移后点坐标与对应的原本点坐标相比，横坐标（即 $x$ 的值）减少了 $1$ 个单位长度，纵坐标（即 $y$ 的值）没有变化。
  因此，我们设平移后的函数图像为 $y=x_1$ , 则 $x_1$ 就是原函数表达式中的 $x$ 减去 $1$ 得来的。为了使 $y=x$ 这个式子成立，要用 $x_1$ 加上 $1$ 表示 $x$ ，就可以得到 $y=x_1+1$ 。这样以来，函数图像 $y=x$ 和 $y=x_1-1$ 的点坐标中，虽然 $x_1$ 和 $x$ 的值不同，但 $y$ 的值是相同的。
  
  所以直线 $y=kx+b\ (k \neq 0)$ 向左平移 $m (m> 0)$ 个单位长度得到直线 $y=k(x+m)+b\ (k \neq 0)$ , 向右平移 $m (m> 0)$ 个单位长度得到直线 $y=k(x-m)+b\ (k \neq 0)$ 。简称“左加右减自变量”。
  如果理解起来仍有困难，可以去听「这个视频」。
  
  注：上文中虽然平移后的图像是一次函数图像，需要设成 $y=kx+b \ (k \neq 0)$ 的形式。但是因为平移且方向是左右，因此要变的是 $x$ 的值，与 $k$ 和 $b$ 无关，又因为在平移前函数表达式中 $b=0$ , 所以就省略了 $b$ 。
快速求一次函数图像与 $x$ 轴，$y$ 轴的交点坐标方法
- 当函数图像 $y=kx+b \ (k \neq 0)$ 中 $y=0$ , $b,k$ 为常数时， $x$ 的值就是函数图像与 $x$ 轴交点的横坐标。
- 当函数图像 $y=kx+b \ (k \neq 0)$ 中 $b$ 的值就是函数图像与 $y$ 轴交点的纵坐标。
  - 所以一般情况下图像与 $x$ 轴的交点坐标为 $(-\frac{b}{k},0)$ ;
  - 与 $y$ 轴交点坐标为 $(0,b)$ ;
$x$ 轴，$y$ 轴的函数关系式及平行于$x$ 轴，$y$ 轴的函数关系式：
- $x$ 轴上的函数关系式为：$y=0$ ；
  设平行于$x$ 轴的直线上点的坐标为 $b$，
  则此直线上的函数关系式为 $y=b \ (b \neq 0)$ ;
- $y$ 轴上的函数关系式为：$x=0$ ；
  设平行于$y$ 轴的直线上点的坐标为 $z$，
  则此直线上的函数关系式为 $y=a \ (a \neq 0)$ ;

4.5 一次函数的应用

4.5.1 正比例函数解析式的求法：

待定系数法：知道一个横纵坐标不为 $0$ 的坐标，代入求得系数 $k$ 的值，就能求出函数解析式。

4.5.2 求一次函数解析式的方法：

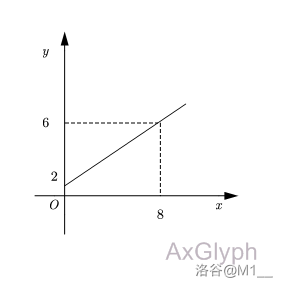
如图，因为两点确定一条直线，所以求一次函数 $y=kx+b \ (k \neq 0)(b \neq 0)$ 就需要两个坐标。上图的是坐标 $(0,2)$ 和 $(8,6)$ ，
把两组坐标代入求值即可。

具体过程：
解：设 $y$ 与 $x$ 的函数关系为 $y=kx+b \ (k \neq 0)$ ;
$\because $ 函数图像 $y=kx+b \ (k \neq 0) $ 经过坐标 $(0,2)(8,6)$ ;
$\therefore \left\{\begin{matrix} b=2\\ 8k+b=6 \end{matrix}\right.$

解得$\left\{\begin{matrix} b=2\\ k=\frac{1}{2} \end{matrix}\right.$
$\therefore \ y$ 与 $x$ 的函数关系式为 $y= \frac{1}{2}x+2 .$

4.5.3 一次函数与图形面积

坐标轴上任意两点的距离求法:
- $x$ 轴上任意两点 $A(x_1,0),B(x_2,0)$ ;
  则 $AB=|x_1-x_2|$
- $y$ 轴上任意两点 $C(0,y_1),D(0,y_2)$ ;
  则 $CD=|y_1-y_2|$ .
象限内任意一点到坐标轴的垂直距离求法：
- 象限内任意一点到 $x$ 轴的垂直距离求法是它纵坐标的绝对值；
- 象限内任意一点到 $y$ 轴的垂直距离求法是它横坐标的绝对值；
  借助上面的方法可以求出有一边在坐标轴上的图形面积（就目前题型来看三角形居多）。
求所有边都不在坐标轴上的图形面积：
一个模型，如下面的例题：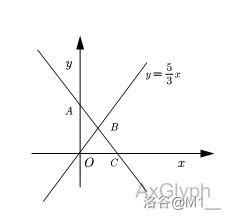

如图，在平面直角坐标系中，一次函数 $y=-\frac{4}{3}x+9$ 的图像与 $y$ 轴相交于点 $A(0,9)$ 与 $x$ 轴相交于点 $C$ ，并与直线 $y=\frac{5}{3}x$相交于点 $B(3,5)$.
当 $Q$ 为直线 $y=-\frac{4}{3}x+9$ 上一动点，当点 $Q$ 运动到何位置时， $\triangle OBQ$ 的面积等于 $\frac{27}{4}$ ? 请求出点 $Q$ 的坐标。
$\because A(0,9),B(3,5)$
$OA=|9|=9$ , $|x_B|=|3|=3$
根据题意分析得三种情况：
- 当 $x_Q<0$ 时，如下图：
  
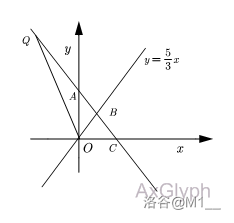
  $S_{\triangle OBQ}=S_{\triangle OAQ}+S_{\triangle OAB}$
  
  ${\frac{1}{2}AO \cdot |x_Q|}+ {\frac{1}{2}AO \cdot |x_B|}=\frac{27}{4}$
  
  $\frac{1}{2}AO(|x_B|+|x_Q|)=\frac{27}{4}$
  
  $\frac{1}{2}AO(3+|x_Q|)=\frac{27}{4}$
  
  解得 $|x_Q|=-\frac{3}{2}$ ;
  $\because |x_Q|>0$
  $\therefore $ 舍去；
- 当 $0 \le x_Q \le 3$ 时，如下图：
  
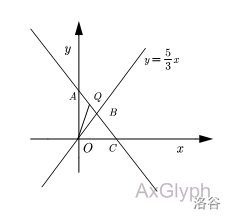
  $S_{\triangle OBQ}=S_{\triangle OAB}-S_{\triangle OAQ}$
  
  $ {\frac{1}{2}AO \cdot x_B}-{\frac{1}{2}AO \cdot x_Q}=\frac{27}{4}$
  
  $\frac{1}{2}AO(x_B-x_Q)=\frac{27}{4}$
  
  $\frac{1}{2}AO(3-x_Q)=\frac{27}{4}$
  
  解得 $x_Q=\frac{3}{2}$ ;
- 当 $x_Q<3$ 时，如下图：
  
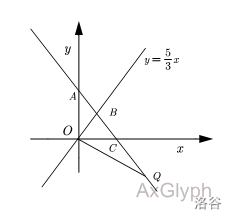
  $S_{\triangle OBQ}=S_{\triangle OAQ}-S_{\triangle OAB}$
  
  $ {\frac{1}{2}AO \cdot x_Q}-{\frac{1}{2}AO \cdot x_B}=\frac{27}{4}$
  
  $\frac{1}{2}AO(x_Q-x_B)=\frac{27}{4}$
  
  $\frac{1}{2}AO(x_Q-3)=\frac{27}{4}$
  
  解得 $x_Q=\frac{9}{2}$ ;
  综上，点 $Q$ 的坐标为 $(\frac{3}{2},7)$ 或 $(\frac{9}{2},3)$ .
通过以上情况的推导，我们可以发现只有两种情况符合题意。所以我们可以概括地这样表示：
$S_{\triangle OBQ}=\frac{1}{2}AO\cdot|x_B-x_Q|$

解得 $x_Q=\frac{3}{2}$ 或 $x_Q=\frac{9}{2}$；

综上，点 $Q$ 的坐标为 $(\frac{3}{2},7)$ 或 $(\frac{9}{2},3)$ .