哈夫曼树学习笔记
定义
设二叉树具有 \(n\) 个带权叶结点,从根结点到各叶结点的路径长度与相应叶节点权值的乘积之和称为 树的带权路径长度(Weighted Path Length of Tree,WPL)。
设 \(w_i\) 为二叉树第 \(i\) 个叶结点的权值,\(l_i\) 为从根结点到第 \(i\) 个叶结点的路径长度,则 WPL 计算公式如下:
\[WPL = \sum_{i = 1}^{n} w_i l_i \]WPL 有什么用呢?我们可以用两种方式理解 WPL。
-
(合并果子)考虑这样的一棵二叉树:它每个节点的权值都是两个子节点的权值之和。我们可以证明:这棵二叉树的 WPL 就是它所有非叶节点的权值之和。而这棵二叉树又可以和这样的情景对应:假设你有 \(n\) 堆苹果,每堆苹果有 \(w_i\) 个。你可以进行 \((n-1)\) 次操作,每次操作把相邻的两堆苹果合并成一堆,消耗的体力是两堆苹果的数量之和。不难看出,经过 \((n-1)\) 次操作后,恰好剩下一堆苹果。
可以发现,每个合并苹果的操作序列,都可以和一棵上述的二叉树对应:二叉树的 \(n\) 个叶节点的权值分别对应一开始每堆苹果的个数,非叶节点的权值代表合并两个子节点消耗的体力。一开始,每堆苹果可以看作是只有一个节点的二叉树。选择两堆苹果合并,就相当于把两颗二叉树的根节点连到一个新建的父节点上,这个父节点的权值就是它两个子节点的权值之和。这样,操作消耗的总体力就是二叉树所有非叶节点的权值之和。上文已经说明,这个值就是二叉树的 WPL。所以,想要最小化消耗的体力,就是要在给定的权值序列上建立一棵二叉树,使得该树的叶节点的权值与原序列的权值一一对应,并且该树的 WPL 最小。(实际上就是这道题:P1090 合并果子)
-
(最优前缀编码)略
这样的 WPL 最小的树,就是哈夫曼树。注意,哈夫曼树的定义是基于某个权值序列来说的:我们是在某个权值序列上构建哈夫曼树。
哈夫曼树的构建及最优性证明
构建
- 初始化:由给定的 \(n\) 个权值构造 \(n\) 棵只有一个根节点的二叉树,得到一个二叉树集合 \(\mathcal{F}\)。
- 选取与合并:从二叉树集合 \(\mathcal{F}\) 中选取根节点权值 最小的两棵 二叉树分别作为左右子树构造一棵新的二叉树,这棵新二叉树的根节点的权值为其左、右子树根结点的权值和。
- 删除与加入:从 \(\mathcal{F}\) 中删除作为左、右子树的两棵二叉树,并将新建立的二叉树加入到 \(\mathcal{F}\) 中。
- 重复 2、3 步,当集合中只剩下一棵二叉树时,这棵二叉树就是霍夫曼树。
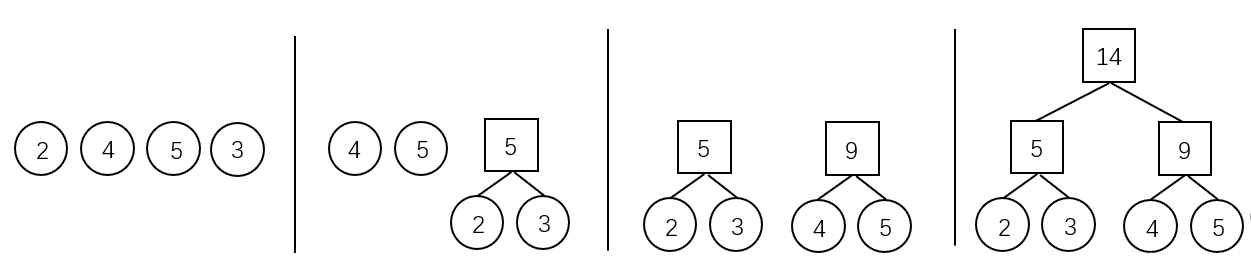
最优性证明
咕咕咕……
代码实现
这里,我们不建树,只求 WPL。
\(O(n \log n)\) 方法
使用一个优先队列维护每棵二叉树的根节点的权值,每次弹出堆顶的两个元素,把这两个元素的和加入队列,同时统计答案。
这个方法比较简单,不再赘述。
cin >> n;
for(int i = 1, x; i <= n; i++)
{
cin >> x;
que.push(x);
}
while(que.size() >= 2)
{
ll a, b;
a = que.top(); que.pop();
b = que.top(); que.pop();
ans += a + b;
que.push(a + b);
}
cout << ans << endl;
\(O(n)\) 方法
上一种方法中的时间复杂度瓶颈来自优先队列,这次我们不用它了,而用两个队列来代替它。
没有优先队列,怎么保证每次取出的元素是两个最小的元素呢?
先考虑初始化的问题。显然,一开始我们还是要保证队列中的元素是递增的。在值域较小时,我们可以采用桶排,这样就做到了 \(O(n)\) 排序。(值域很大怎么办?可以使用基数排序,但我还不会)
然后我们采用如下算法:
-
把排序后的初始元素依次插入队列 1 中。此时队列 2 为空。
-
每次从队列 1 和队列 2 首共弹出两个元素,使得这两个元素的和最小。分三种情况:
- 从队列 1 首弹出两个元素。
- 从队列 2 首弹出两个元素。
- 从队列 1 首和队列 2 首分别弹出一个元素。
分类讨论即可。
-
计算这两个元素的和,并插入队列 2 尾。同时答案加上这个和。
-
重复步骤 2、3 \((n-1)\) 次。
这个算法与 \(O(n \log n)\) 的算法的区别主要在于第 2 步。要证明它的正确性,只需证明第 2 步中弹出的两个元素就是最小的两个元素即可。
由于一开始,我们就已将元素排序再插入进队列 1 中,而之后我们不会向队列 1 中插入任何元素,所以队列 1 中元素时刻都是递增的。而由于我们每次弹出的是最小的两个元素,所以越往后,弹出元素的和是递增的。我们把弹出元素的和插入到队列 2 中,所以队列 2 中元素也是时刻保持递增的。加上第 2 步中我们讨论了三种情况,这就保证了弹出的两个元素一定是最小的两个元素。故算法的正确性得证。
cin >> n;
for(int i = 1, x; i <= n; i++)
{
read(x);
cnt[x]++;
}
for(int i = 1; i < MAXV; i++)
while(cnt[i]) que1.push(i), cnt[i]--;
for(int i = 1; i < n; i++)
{
ll a, b;
if((!que1.empty() && que1.front() < que2.front()) || que2.empty())
a = que1.front(), que1.pop();
else a = que2.front(), que2.pop();
if((!que1.empty() && que1.front() < que2.front()) || que2.empty())
b = que1.front(), que1.pop();
else b = que2.front(), que2.pop();
que2.push(a + b), ans += a + b;
}
cout << ans << endl;
\(k\) 叉哈夫曼树
哈夫曼树也可以推广到 \(k\) 叉的情况。
考虑 \(k\) 进制下的最优前缀编码问题:每个单词用一个 \(k\) 进制代码表示,求出最短的编码方案。这等价于在一个权值序列上建立一棵 \(k\) 叉树,使得 WPL 最小。
这个问题几乎可以完全套用二叉哈夫曼树的构建方法,只需要把每次合并两棵树改成每次合并 \(k\) 棵树即可。但有个小问题:合并到最后,可能只剩下不到 \(k\) 棵树,于是最终的树的根节点度数小于 \(k\),这是不优的:任取某个叶节点改为根的子节点,都会使 WPL 变小。
解决这个问题的方法是在权值序列中加入若干个 \(0\),使得最后恰好剩下 \(k\) 棵树。加入多少个 \(0\) 呢?我们每次弹出 \(k\) 棵树,加入 \(1\) 棵树,相当于每次操作后树的数量减少了 \(k-1\)。而最后恰好留下一棵树,所以一开始应该满足 \((n - 1) \bmod (k-1) = 0\)。
如果在满足 WPL 最小的情况下,还要让最深的叶节点的深度尽可能小,应该怎么办?
在优先队列中,还要根据每棵树的深度排序:如果根节点权值不同,优先合并权值小的;如果权值相同,优先合并深度小的。但我还没搞懂为什么……