首页 > 其他分享 >单调队列优化 && 斜率优化

单调队列优化 && 斜率优化

时间：2024-07-23 15:07:13浏览次数：16  
标签：int sumc tt tr 斜率 && 优化 dp

单调队列优化 dp 浅学

1. 概念

单调队列优化的本质是借助单调性，及时排除不可能的决策，保持候选集合的秩序性。

2. 例题

P1714 切蛋糕

题目大意：

给定一个序列，找出长度不超过 \(m\) 的连续子序列，使得子序列中所有数的和最大。

思路：

要求区间和，首先求出前缀和，然后考虑朴素 dp，不难想到用 \(dp[i]\) 表示包含 \(a[i]\) 的连续子序列中的最大和，那么状态转移方程为：

\[dp[i] = \max\limits_{i - m\le j\le i - 1} \{sum[i] - sum[j]\} \]

所以朴素代码很快就能出炉：

#include <cstring>
#include <iostream>

using namespace std;

const int N = 500010;

int n, m;
int sum[N], dp[N];
int ans;

int main() {
    scanf("%d%d", &n, &m);
    int x;
    for(int i = 1; i <= n; i++) {
        scanf("%d", &x);
        sum[i] = sum[i - 1] + x;
    }   
    memset(dp, -0x3f, sizeof dp);
    for(int i = 1; i <= n; i++) {
        for(int j = max(i - m + 1, 0); j <= i; j++)
            dp[i] = max(dp[i], sum[i] - sum[j - 1]);
        ans = max(ans, dp[i]);
    }
    printf("%d\n", ans);
    return 0;
}

时间复杂度为 \(O(n^2)\)，不能够通过此题，考虑优化。

顺便提一句动态规划的优化思路：

一个原则：

在朴素代码上做等价变形。

三个方向：

  1. 优化状态设计，阶段和状态转移方程；
  2. 若有状态被多次计算或调用，则考虑加上记忆化搜索；
  3. 若有多层循环，考虑将与外层循环相关的变量看作定值，及时排除内层循环中的不可能决策或利用数据结构等方法优化找最值的过程，从而优化掉内层循环。

很显然，这道题我们选择方向 \(3\)。

容易发现，在外层循环到 \(i\) 时，\(sum[i]\) 是确定的，改变的只是 \(sum[j]\)，所以，我们将状态转移方程整理一下，得：

\[dp[i] = sum[i] - \min\limits_{i - m\le j\le i - 1} \{sum[j]\} \]

所以，内层循环的作用其实是寻找 \(sum\) 数组中区间 \([i - m,i - 1]\) 的最小值，且当外层 \(i\) 变为 \(i+ 1\) 时，区间变成 \([i - m + 1,i]\)，这意味着只需要将 \(j = i\) 加入候选决策集合并将 \(j = i - m\) 从决策集合中移除即可。

是不是和滑动窗口如出一辙？

所以我们可以用单调队列来优化这个找最小值的过程。

\(\texttt{Code:}\)

#include <cstring>
#include <iostream>

using namespace std;

const int N = 500010;

int n, m;
int sum[N];
int q[N], hh, tt = -1;
int ans = -0x3f3f3f3f;

int main() {
    scanf("%d%d", &n, &m);
    int x;
    for(int i = 1; i <= n; i++) {
        scanf("%d", &x);
        sum[i] = sum[i - 1] + x;
    }
    for(int i = 1; i <= n; i++) {
        if(hh <= tt && i - m - 1 >= q[hh]) hh++;
        while(hh <= tt && sum[i - 1] <= sum[q[tt]]) tt--;
        q[++tt] = i - 1;
        ans = max(ans, sum[i] - sum[q[hh]]);
    }
    printf("%d\n", ans);
    return 0;
}

总结：

在状态转移方程中当前状态的所有值可以从上一个状态的某个连续的段的值得到，要对这个连续的段进行 RMQ 操作，相邻状态的段的左右区间满足非降的关系时，就可以使用单调队列优化 dp。

斜率优化浅学

1. 基本形式

\[dp[i] = \min\limits_{L(i)\le j\le R(i)} \text{(或max)}\{dp[j] + val(i,j)\} \]

其中与单调队列优化不同的是，单调队列优化的针对对象是多项式 \(val(i,j)\) 的每一项仅与 \(i\) 或 \(j\) 有关的情况。

斜率优化针对的是多项式 \(val(i,j)\) 包含 \(i,j\) 的乘积项的情况。

2. 例题

P2365 任务安排

思路

可见这是个序列问题，考虑将目前处理到第几位作为阶段来划分，即令 \(dp[i]\) 表示把前 \(i\) 个任务处理完的最小花费。

枚举最后一次分批在哪个位置，设为 \(j\)，$0\le j < i $。

所以最后一批任务即为 \(j + 1\sim i\)。

所以状态转移方程为：

\[dp[i] = \min\limits_{0\le j < i}\{dp[j] + val(j + 1,i)\} \]

其中 \(val(j + 1,i)\) 表示第 \(j + 1\sim i\) 个任务带来的花费。

前 \(j\) 个任务的最小花费即为 \(dp[j]\)，所以只需计算 \(val(j + 1, i)\)。

难点在于花费的计算和完成任务的时间有关，机器启动时间 \(S\) 会对后面的阶段造成影响，所以这里需要用到 “费用提前计算” 的思想，提前算出启动时间 \(S\) 带来的额外花费。

用 \(sumt[i]\) 来表示要完成前 \(i\) 个任务所需的时间和，\(sumc[i]\) 表示前 \(i\) 个任务的费用系数总和，都可以用前缀和提前求出。

综上所述：状态转移方程为：

\[dp[i] = \min\limits_{0\le j < i}\{dp[j] + sumt[i] * (sumc[i] - sumc[j]) + S * (sumc[n] - sumc[j])\} \]

时间复杂度为 \(O(n^2)\)，可以通过此题。

\(\texttt{Code:}\)

#include <cstring>
#include <iostream>

using namespace std;

const int N = 5010;
typedef long long ll;

int n, S;
ll sumt[N], sumc[N];
ll dp[N];

int main() {
    scanf("%d%d", &n, &S);
    for(int i = 1; i <= n; i++) {
        scanf("%d%d", &sumt[i], &sumc[i]);
        sumt[i] += sumt[i - 1];
        sumc[i] += sumc[i - 1];
    }
    memset(dp, 0x3f, sizeof dp);
    dp[0] = 0;
    for(int i = 1; i <= n; i++)
        for(int j = 0; j < i; j++)
            dp[i] = min(dp[i], dp[j] + sumt[i] * (sumc[i] - sumc[j]) + S * (sumc[n] - sumc[j]));
    printf("%lld", dp[n]);
    return 0;
}

加强版：

AcWing 301. 任务安排2

题目描述一样，但 \(n\le 3 * 10^5\)，考虑优化。

对状态转移方程进行整理，合并同类项，得：

\[dp[i] = \min\limits_{0\le j < i}\{dp[j] - (S + sumt[i]) * sumc[j]\} + sumt[i] * sumc[i] + S * sumc[n] \]

对于每个 \(j\)，去掉 \(\min\)，得：

\[dp[i] = dp[j] - (S + sumt[i]) * sumc[j] + sumt[i] * sumc[i] + S * sumc[n] \]

根据上文提到的方向 \(3\)，和外层循环 \(i\) 相关的值可以暂时看成常量，所以原式的变量就只有 \(dp[j]\) 和 \(sumc[j]\)，分别看成 \(y\) 和 \(x\)，整理得：

\[y = (S + sumt[i]) * x + dp[i] - sumt[i] * sumc[i] - S * sumc[n] \]

有点眼熟……再多看一眼……这不是直线斜截式 \(y = kx + b\) 吗？

以 \(sumc[j]\) 为横坐标， \(dp[j]\) 为纵坐标，建立平面直角坐标系，所以这是一条斜率为 \(S + sumt[i]\)，截距为 \(dp[i] - sumt[i] * sumc[i] - S * sumc[n]\) 的直线。

也就是说，决策候选集合是坐标系的一个点集，每个决策 \(j\) 都对应一个点 \((sumc[j], dp[j])\)。

这样一来，状态转移方程就变为了 \(b_i = \min\limits_{0\le j < i}\{y_i - k_ix_i\}\)

因为要求的 \(dp[i]\) 是 \(b_i\) 中一个系数为正的项，所以问题转化成了：坐标系中有一些点 \((x_j,y_j)\)，从中选出一个点，使得经过它，且斜率为 \(k_i\) 的直线的截距最小。

形象一点来说就是有一根斜率为 \(k_i\) 的直线从负无穷开始逐渐上移，直到它碰到点集中的点。

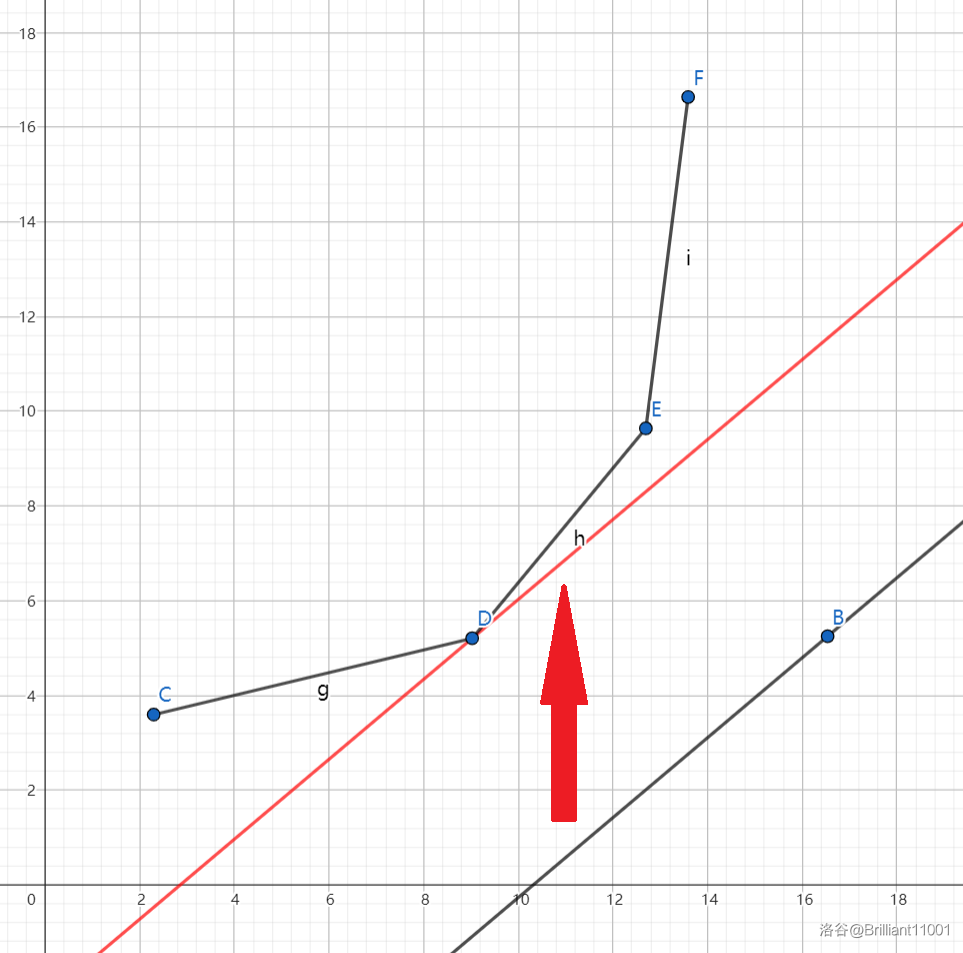
如图所示，点 \(D\) 就是我们要找的最佳决策点。

观察图像不难发现，只有当 \((x_j,y_j)\) 位于下凸壳时，\(j\) 才可能被作为最优决策，所以我们不需要维护整个点集，只需要维护一个下凸壳就行了。

算完 \(dp[i]\) 我们就要把点 \((x_i,y_i)\) 插入点集中，那么如何维护点集才能使我们能快速地找到最优决策呢？

解法一：

首先想到：可以用二分。观察，思考什么时候 \((x_j,y_j)\) 可以作为最优决策呢？

可以发现，当 \((x_j,y_j)\) 与它的上一个点 \((x_{j-1},y_{j-1})\) 构成的直线的斜率小于 \(k_i\)，且与它的下一个点 \((x_{j+1},y_{j+1})\) 构成的直线的斜率大于 \(k_i\) 时，\(j\) 为最优决策点。

我们先用一个容器（这里选用队列）来存储目前的点集，然后二分求第一个和上一个点构成的直线斜率小于 \(k_i\) 且和后一个点构成的直线斜率大于 \(k_i\) 的点。

然后用二分出的答案来计算 \(dp[i]\)。

再插入决策 \(i\)，这时要维护下凸壳，检查队尾 \(q[tt]\)、 \(q[tt - 1]\) 和要加入的 \(i\) 是否构成一个下凸壳，具体地，当

\[\frac{dp[q[tt]] - dp[q[tt - 1]]}{sumc[q[tt]] - sumc[q[tt - 1]]} \ge \frac{dp[i] - dp[q[tt]]}{sumc[i] - sumc[q[tt]]} \]

时，就应该将队尾弹出。

这样就可以将时间复杂度优化到 \(O(n\log n)\)。

\(\texttt{Code:}\)

#include <iostream>

using namespace std;

const int N = 300010;
typedef long long ll;
int n, S;
ll sumt[N], sumc[N];
ll dp[N];
int q[N], hh, tt = -1;

int main() {
    scanf("%d%d", &n, &S);
    for(int i = 1; i <= n; i++) {
        scanf("%lld%lld", &sumt[i], &sumc[i]);
        sumt[i] += sumt[i - 1];
        sumc[i] += sumc[i - 1];
    }
    q[++tt] = 0;
    for(int i = 1; i <= n; i++) {
        int l = hh, r = tt;
        while(l < r) {
            int mid = l + r >> 1;
            if(dp[q[mid + 1]] - dp[q[mid]] > (sumt[i] + S) * (sumc[q[mid + 1]] - sumc[q[mid]])) r = mid;
            else l = mid + 1;
        }
        dp[i] = dp[q[l]] - (S + sumt[i]) * sumc[q[l]] + sumt[i] * sumc[i] + S * sumc[n];
        while(hh < tt && (__int128)(dp[q[tt]] - dp[q[tt - 1]]) * (sumc[i] - sumc[q[tt]]) >= (__int128)(dp[i] - dp[q[tt]]) * (sumc[q[tt]] - sumc[q[tt - 1]])) tt--;
        q[++tt] = i;
    }
    printf("%lld", dp[n]);
    return 0;
}

解法二

注意到这道题有个特殊条件：\(T_i,C_i\) 都是正整数，意思就是说 \(sumt\) 和 \(sumc\) 数组一定是单调递增的，所以我们只会不断地在右边加点，而且 \(k_i\) 是单调递增的。

外层循环每增加 \(1\)，就会新加入一个决策点，同时由于斜率会变大，就可能导致前面的一些决策没用了，要及时排除，只保留凸包上相邻两点连线斜率大于 \(k_i\) 的部分，那么凸包最左端的点一定就是最优决策点。

这启示我们可以用单调队列来维护凸包。

建立一个单调队列 \(q\)，当外层循环 \(i\) 增加 \(1\) 后：

  1. 排除无用决策，检查队头元素 \(q[hh]\) 和 \(q[hh + 1]\) 构成的直线的斜率是否小于等于当前斜率，具体地，当

\[\frac{dp[q[hh + 1]] - dp[q[hh]]}{sumc[q[hh + 1]] - sumc[q[hh]]} \le sumt[i] + S \]

时，就应该将队头弹出；

  1. 取出队头 \(j = q[hh]\) 为最优决策，用它来计算 \(dp[i]\)；

  2. 即将要把 \(i\) 插入队尾，检查队尾 \(q[tt]\)、 \(q[tt - 1]\) 和要加入的 \(i\) 是否构成一个下凸包，具体地，当

\[\frac{dp[q[tt]] - dp[q[tt - 1]]}{sumc[q[tt]] - sumc[q[tt - 1]]} \ge \frac{dp[i] - dp[q[tt]]}{sumc[i] - sumc[q[tt]]} \]

时，就应该将队尾弹出。

时间复杂度为 \(O(n)\)。

\(\texttt{Code:}\)

#include <cstring>
#include <iostream>

using namespace std;

const int N = 300010;
typedef long long ll;

int n, S;
ll sumt[N], sumc[N];
int q[N], hh, tt = -1;
ll dp[N];

int main() {
    scanf("%d%d", &n, &S);
    for(int i = 1; i <= n; i++) {
        scanf("%lld%lld", &sumt[i], &sumc[i]);
        sumt[i] += sumt[i - 1];
        sumc[i] += sumc[i - 1];
    }
    q[++tt] = 0;
    for(int i = 1; i <= n; i++) {
      	//为防止浮点除法导致精度丢失，故交叉相乘，但要注意极端数据会爆 long long，需使用 __int128
        while(hh < tt && (__int128)(dp[q[hh + 1]] - dp[q[hh]]) <= (__int128)(sumt[i] + S) * (sumc[q[hh + 1]] - sumc[q[hh]])) hh++;
        int j = q[hh];
        dp[i] = dp[j] - sumc[j] * (sumt[i] + S) + sumt[i] * sumc[i] + sumc[n] * S;
        while(hh < tt && (__int128)(dp[q[tt]] - dp[q[tt - 1]]) * (sumc[i] - sumc[q[tt]]) >= (__int128)(dp[i] - dp[q[tt]]) * (sumc[q[tt]] - sumc[q[tt - 1]])) tt--;
        q[++tt] = i;
    }
    printf("%lld", dp[n]);
    return 0;
}

然鹅，对于一些数据及其毒瘤的题，不仅斜率可能不单调递增，而且横坐标也可能不单调递增，我们分别来看一下这两种情况。

1. 横坐标单增，斜率不单增

P5785 [SDOI2012] 任务安排

题意相同，但 \(T_i\) 可能为负数，也就是说 \(sumt\) 数组不一定单调递增，也就导致斜率可能一会儿大，一会儿小，单调队列的方法行不通了，就只能采用解法一：二分来做。

2. 横坐标不单增，斜率单增

目前没有遇到这种题。

横坐标不单增，意味着可能需要在中间某个地方插入点，但单调队列还是可以用的，这时可以在单调队列中二分插入，但这样单调队列就要写成“单调链表”了，感觉不太好写。

3. 横坐标不单增，斜率也不单增

P4655 [CEOI2017] Building Bridges

不得不说这种题真的毒瘤。

首先推柿子，令 \(dp[i]\) 表示第 \(i\) 根柱子和一号柱子连通的最小花费，那么状态转移方程就可以一眼顶针为：

\[dp[i] = \min\limits_{1\le j < i}\{dp[j] + (h[i] - h[j])^2 + sumw[i - 1] - sumw[j]\} \]

其中 \(sumw[i]\) 表示前 \(i\) 根柱子的拆除代价之和。

将柿子展开整理，得：

\[dp[j] + (h[j])^2 - sumw[j] = 2 * h[i] * h[j] - (h[i])^2 - sumw[i - 1] \]

于是就是很明显的斜率优化，令 \(Y = dp[j] + (h[j])^2 - sumw[j],\space X = h[j]\)。

所以 \(Y = 2*h[i] * X + dp[i] - (h[i])^2 - sumw[i - 1]\)

但是发现斜率 \(2 * h[i]\) 不单调，\(X\) 也不单调，之前的方法都没法用了。

这时候就应该拿出斜率优化三件套了：李超线段树、cdq 分治、平衡树。

但是蒟蒻不会前两个，只能选择平衡树。

解释一下为什么是平衡树。

我们需要一个数据结构，支持以下操作：

  1. 插入一个点 \((x,y)\)；
  2. 查询第一个横坐标小于 \(x\) 的点的下标；
  3. 查询第一个横坐标大于 \(x\) 的点的下标；
  4. 删除一个点;
  5. 查询第一个 “和左边点组成的直线斜率小于 \(k\)，且和右边点组成的直线斜率大于 \(k\) 的点” 的下标。

综上所述，平衡树是最符合条件的数据结构。

我选择了最灵活的 Splay 来维护凸包。

\(\texttt{Code:}\)

#include <cmath>
#include <cstring>
#include <iostream>

using namespace std;

const int N = 100010;
const double eps = 1e-10, inf = 1e15; //注意精度
typedef long long ll;
int n;
ll h[N], sumw[N], dp[N];
struct node{
    int s[2], p;
    double xs, ys, lk, rk;
    void init(int p_, double xs_, double ys_) {p = p_, xs = xs_, ys = ys_;}
}tr[N];
int root, idx;
inline double X(int x) {return h[x];} //横坐标
inline double Y(int x) {return dp[x] + h[x] * h[x] - sumw[x];} //纵坐标
inline double slope(int i, int j) {
    if(fabs(tr[i].xs - tr[j].xs) < eps) return tr[i].ys < tr[j].ys ? inf : -inf; //特判直线垂直于 x 轴的情况
    return (tr[i].ys - tr[j].ys) / (tr[i].xs - tr[j].xs);
}

void rotate(int x) {
	int y = tr[x].p, z = tr[y].p;
	int k = x == tr[y].s[1];
	tr[z].s[y == tr[z].s[1]] = x, tr[x].p = z;
	tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
	tr[x].s[k ^ 1] = y, tr[y].p = x;
}

inline void splay(int x, int k) {
    while(tr[x].p != k) {
        int y = tr[x].p, z = tr[y].p;
        if(z != k) {
            if((x == tr[y].s[1]) ^ (y == tr[z].s[1])) rotate(x);
            else rotate(y);
        }
        rotate(x);
    }
    if(!k) root = x;
}

inline void insert(double xs, double ys) {
    int u = root, p = 0;
    while(u) p = u, u = tr[u].s[xs + eps > tr[u].xs];
    u = ++idx;
    if(p) tr[p].s[xs + eps > tr[p].xs] = u;
    tr[u].init(p, xs, ys);
    splay(u, 0);
}

inline int get_prev(int x) {
    int res = 0, u = tr[x].s[0];
    while(u) {
        if (tr[u].lk < slope(u, x) + eps) res = u, u = tr[u].s[1]; //只寻找满足凸包性质的点
        else u = tr[u].s[0];
    }
    return res;
}

inline int get_next(int x) {
    int res = 0, u = tr[x].s[1];
    while(u) {
        if (slope(x, u) < tr[u].rk + eps) res = u, u = tr[u].s[0]; //只寻找满足凸包性质的点
        else u = tr[u].s[1];
    }
    return res;
}
//以上为 Splay 模板

//维护凸壳
inline void update(int &rt, int x) {
    splay(x, 0);
    if (tr[x].s[0]) {
        int y = get_prev(x);
        if(y) { //有可能有左子树但左子树上的点都不满足凸包性质，所以要特判
            splay(y, x);
            tr[y].s[1] = 0; // 清空那些不满足凸包性质的点
            tr[y].rk = tr[x].lk = slope(y, x); //计算斜率
        }
        else tr[x].s[0] = 0, tr[x].lk = -inf; //左边没有点能满足凸包性质，全部删掉且斜率为负无穷
    } else tr[x].lk = -inf;
    if (tr[x].s[1]) { //同上
        int y = get_next(x);
        if(y) {
            splay(y, x);
            tr[y].s[0] = 0;
            tr[x].rk = tr[y].lk = slope(x, y);
        }
        else tr[x].s[1] = 0, tr[x].rk = inf;
    } else tr[x].rk = inf;
    if (tr[x].lk + eps > tr[x].rk) { //若左斜率大于右斜率，则说明不满足凸包性质，删掉
        int y = get_prev(x), z = get_next(x);
        splay(y, 0), splay(z, y);
        tr[z].s[0] = 0;
        tr[y].rk = tr[z].lk = slope(y, z); //重新更新斜率
    }
}

//寻找最优决策
//在 Splay 上二分求解
//若当前斜率在左右斜率之间，则找到
//若当前点的左斜率小于当前斜率，说明要求的点在左侧，递归左子树
//否则在右侧，递归右子树
int get_strategy(int u, double k) {
    if(!u) return 0;
    if(tr[u].lk < k + eps && k < tr[u].rk + eps) return u;
    if(tr[u].lk + eps > k) return get_strategy(tr[u].s[0], k);
    else return get_strategy(tr[u].s[1], k);
}

int main() {
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) scanf("%lld", &h[i]);
    for(int i = 1; i <= n; i++) {
        scanf("%lld", &sumw[i]);
        sumw[i] += sumw[i - 1];
    }
    dp[1] = 0;
    dp[2] = dp[1] + (h[2] - h[1]) * (h[2] - h[1]);
    insert(X(1), Y(1));
    update(root, 1);
    insert(X(2), Y(2));
    update(root, 2); //先插入两个基本决策点，方便计算斜率
    for(int i = 3; i <= n; i++) { 
        int j = get_strategy(root, 2.0 * h[i]); //获取最优决策
        dp[i] = dp[j] + (h[i] - h[j]) * (h[i] - h[j]) + sumw[i - 1] - sumw[j]; //更新
        insert(X(i), Y(i));
        update(root, i); //插入新决策并维护凸包
    }
    printf("%lld", dp[n]);
    return 0;
}

（纯纯毒瘤，调了一个上午 + 下午的一节课时间）

汇总一下各道斜率优化的题：

横坐标单增，斜率也单增

P3195 [HNOI2008] 玩具装箱
P4360 [CEOI2004] 锯木厂选址
P2120 [ZJOI2007] 仓库建设
P3648 [APIO2014] 序列分割
P2900 [USACO08MAR] Land Acquisition G
P4072 [SDOI2016] 征途
P3628 [APIO2010] 特别行动队

横坐标单增，斜率不单增

P5785 [SDOI2012] 任务安排

横坐标不单增，斜率也不单增

P4655 [CEOI2017] Building Bridges
P4027 [NOI2007] 货币兑换

标签：int,sumc,tt,tr,斜率,&&,优化,dp
From： https://www.cnblogs.com/Brilliant11001/p/18318473

相关文章

  • scanf、cin及其优化、快读性能测试
    为了让大家了解C++各种IO方式的性能，于是就有了这篇文章。本次测试采取的数据均为\(10^6\)个不超过\(10^8\)随机正整数。测试代码：#include<bits/stdc++.h>usingnamespacestd;intx;intmain(){ freopen("test.in","r",stdin); freopen("test.out","w",stdout......
  • 代码改进，代跑通，预测模型，模型优化
    代码改进，代跑通，预测模型，模型优化，增加模块，python代做，预测，微调，融合，强化学习，深度学习，机器学习程序代写，环境调试，代码调通，模型优化，模型修改，时间序列，机器学习数据处理等开发工程项目主攻:Pytorch,Tensorflow,Yolo,Unet,DNN,CNN,GAN,Transformer,matlab训练模型，优化，price代跑增......
  • P10480 可达性统计（拓扑，bitset 优化）
    link从数的角度来看，如果知道任意一个点能到达的点的数量，那么它的前驱节点一定也能到达，但是，只累加数的话无法处理可能存在重合点的情况。所以，考虑从集合的角度，设\(f(x)\)表示\(x\)能到达的点的集合如果\(x\)有邻点\(y_1,y_2,...,y_k\)，那么\(x\)能到达的点就是它的邻点......
  • Pandas：递归的性能优化
    我有一个代码，看起来像forindex,rowindata.iterrows():data.loc[index,"myCol"]=someFunc(data.loc[index-1,"myCol")该代码正在使用递归，因此我无法对其进行矢量化，因为在许多与iterrows性能相关的问题中都建议使用递归。我在性能方面优化它的最佳方法是什......
  • 魔改Transformer！9种提速又提效的模型优化方案
    Transformer目前已经成为人工智能领域的主流模型，应用非常广泛。然而Transformer中注意力机制计算代价较高，随着序列长度的增加，这个计算量还会持续上升。为了解决这个问题，业内出现了许多Transformer的魔改工作，以优化Transformer的运行效率。我这次就给大家分享9篇对Transform......
  • SQL批量插入的优化心得
    pkgRiskDataVOList=mapper.getBuyAndSaleFee(ImmutableMap.ofEntries(kv("iTradeDate",iTradeDate)));StringfnFmtNumber16=pkiPub.fnFmtNumber(pkgRiskDataVOList.getBuyFee(),6);StringfnFmtNumber17=pkiPub......
  • 【视频】Python遗传算法GA优化SVR、ANFIS预测证券指数ISE数据-CSDN博客
    全文链接：https://tecdat.cn/?p=37060本文旨在通过应用多种机器学习技术，对交易所的历史数据进行深入分析和预测。我们帮助客户使用了遗传算法GA优化的支持向量回归（SVR）、自适应神经模糊推理系统（ANFIS）等方法，对数据进行了特征选择、数据预处理、模型训练与评估。实验结果表明，这些方法......
  • Java中的虚拟线程与并发编程优化
    Java中的虚拟线程与并发编程优化大家好，我是微赚淘客系统3.0的小编，是个冬天不穿秋裤，天冷也要风度的程序猿！今天我们将深入探讨Java中的虚拟线程及其对并发编程的优化。虚拟线程是Java21引入的一个新特性，它可以显著提高应用的并发性能，并简化线程的管理。我们将介绍虚拟线程的基本概......
  • Luogu P4310 绝世好题 题解 [ 绿 ] [ 线性 dp ] [ 单调队列优化 ] [ 二进制优化 ]
    题目：绝世好题。暴力dp显然\(O(n^2)\)转移即可。单调队列优化观察到只有某二进制位两个数都为\(1\)时才能转移，因此我们把每个二进制位开一个单调队列，然后对于一个数\(a\)，找到它是\(1\)的二进制位并选其单调队列的队头进行转移，在这之后把这个数加入符合要求的单调队列......
  • Tomcat部署及优化（企业网站架构部署与优化）
    本章结构Tomcat三个容器Tomcat由一系列的组件构成,其中核心的组件有三个:1：web容器:完成web服务器的功能。2：Servlet容器:名字为catalina，用于处理Servlet代码。3：JSP容器:用于将JSP动态网页翻译成Servlet代码。JSP容器JSP全称JavaServerPages，是一种动态网页开......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99