文章有点长,都是由本人一点一点写出来的,公式加载需要一段时间。
CF1152E Neko and Flashback
思路来自 @apple365。
思路
任意一组 \(b_i, c_i\) 都是相邻的两条边,所以我们将 \(b_i\) 和 \(c_i\) 连起来,如果可以跑通一条欧拉路径,那么这条欧拉路径上的所有数字就可以组成数组 \(a\)。
具体步骤为:
- 将 \(b, c\) 离散化;
- 对于每一组 \(b_i, c_i\), 特判 \(b_i > c_i\) 为无解。
- 否则在 \(b_i\) 和 \(c_i\) 间连接一条双向边。
- 最后看看是否存在欧拉路径,如果存在欧拉路径还要判断路径长度是否为 \(n\),如果都满足则输出。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 200010;
struct edge {
int to, next;
} e[N * 2];
int head[N], idx = 1, d[N];
void add(int u, int v) {
idx++, e[idx].to = v, e[idx].next = head[u], head[u] = idx;
idx++, e[idx].to = u, e[idx].next = head[v], head[v] = idx;
d[u]++, d[v]++;
}
int n, a[N], b[N], c[N], cnt;
vector<int> ans;
void dfs(int u) {
for (int i = head[u]; i; i = head[u]) {
head[u] = e[i].next;
if (e[i].to) {
e[i ^ 1].to = 0;
dfs(e[i].to);
}
}
ans.push_back(u);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i < n; i++) cin >> a[i], c[i] = a[i];
for (int i = 1; i < n; i++) cin >> b[i], c[i + n - 1] = b[i];
for (int i = 1; i < n; i++) {
if (a[i] > b[i]) {
cout << "-1\n";
return 0;
}
}
sort(c + 1, c + 2 * n - 1);
cnt = unique(c + 1, c + 2 * n - 1) - c - 1;
for (int i = 1; i < n; i++) a[i] = lower_bound(c + 1, c + cnt + 1, a[i]) - c;
for (int i = 1; i < n; i++) b[i] = lower_bound(c + 1, c + cnt + 1, b[i]) - c;
for (int i = 1; i < n; i++) add(a[i], b[i]);
int x = 0, st = -1;
for (int i = 1; i <= cnt; i++) {
if (d[i] & 1) x++, st = i;
}
if (x != 0 && x != 2) {
cout << "-1\n";
return 0;
}
if (st == -1) st = 1;
dfs(st);
if (ans.size() != n) {
cout << "-1\n";
return 0;
}
reverse(ans.begin(), ans.end());
for (auto x : ans) cout << c[x] << ' ';
return 0;
}
P5752 [NOI1999] 棋盘分割
这个题解思路虽然与其他人的思路相同,
但力求使用清晰易懂的图片和文字,讲解最简洁的道理。
请大家耐心地看完,注意要结合图片一起哦~~
2022-8-24 更改了格式与错别字。
2022-8-28 更改了数学公式格式。
这是本蒟蒻第一次写题解,不足之处请多包涵。
题目大意:
读完题的可以跳过这一部分。
给定一个矩阵,每个位置上都有数字。
可以分割 \(n-1\) 次,每次分割为 \(2\) 个矩形,然后把一半放在一旁,然后在另外一半继续割。
像这样:
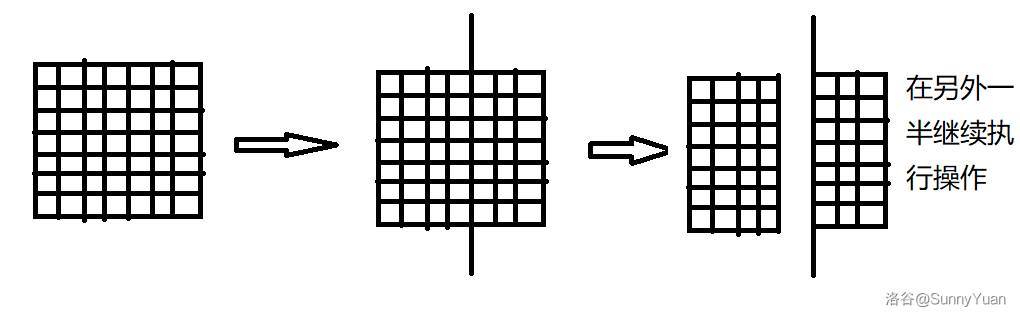
可以横切也可以纵切。
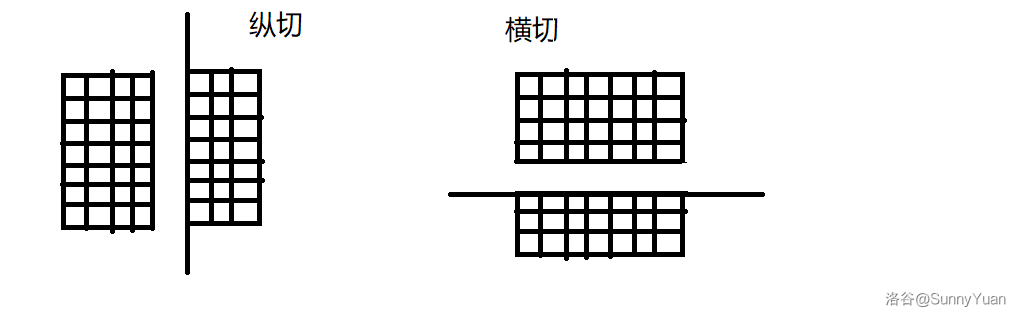
样例给的很好。
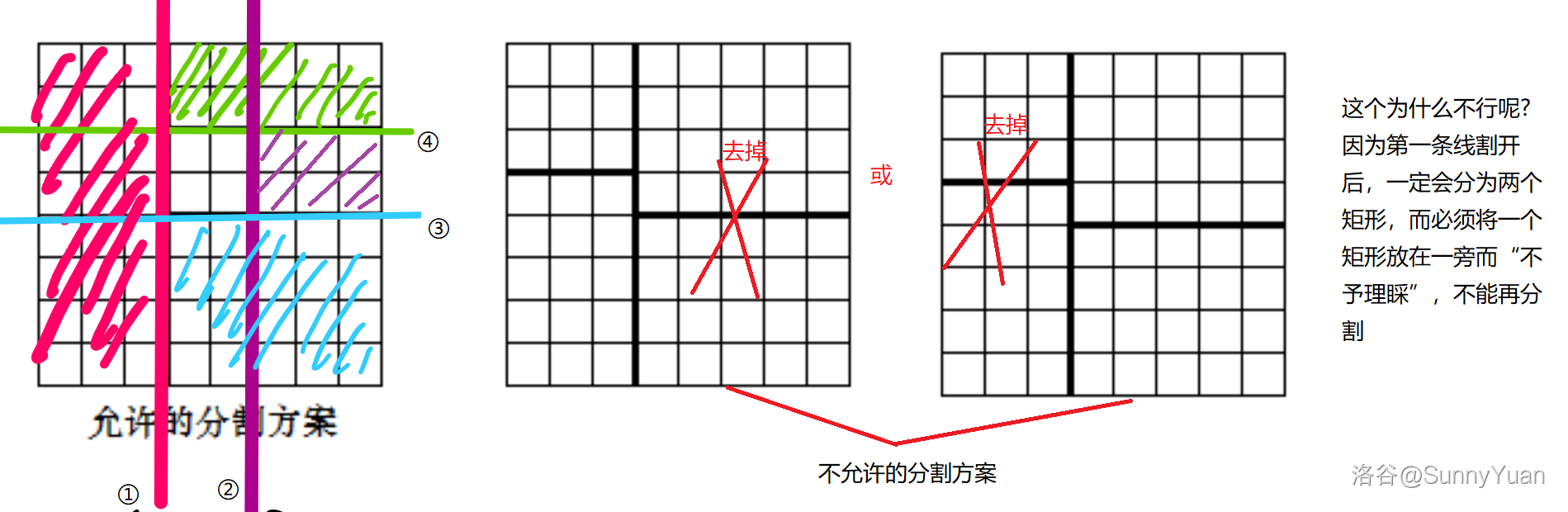
然后就分为 \(n\) 块(因为割了 \(n-1\) 次)。
记 \(X=\dfrac{s}{n}\),\(s\) 为矩阵中所有的数字之和。
设第 \(i\) 块的和为 \(x_i\),那么求出怎样割才能使 $\sum_{i=1}{n}(x_i-X)2 $ 更小。
分析问题:
我们看到这种分割问题,最后组合起来求总体最优值,便可以立马联想到区间 DP。这叫望梅止渴做 DP 问题的复杂反射。
毕竟区间 DP 的主要思想就是大区间包含小区间,
小区间汇集成大区间。
好了,废话不多说,我们先从如下几个角度思考:
- 状态表示
- 状态含义
- 目标状态
- 状态转移
一、状态表示:\(f(x1,y1,x2,y2,k)\)。
二、状态含义:\(f(x1,y1,x2,y2,k)\) 表示求解子矩阵 \((x1,y1)\sim(x2,y2)\) 割了 \(k\) 刀得来的最优解(即下图框住区域的最优解)。
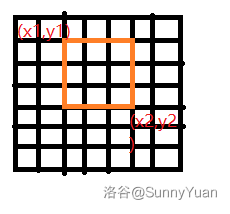
三、目标状态:\(f(1,1,8,8,n)\),即求解整个矩阵被割了 \(n\) 刀的最优解。
四、状态转移:
我们以下图为例,讲解 \(f(x1,y1,x2,y2,k)\) 是如何被拆分的。
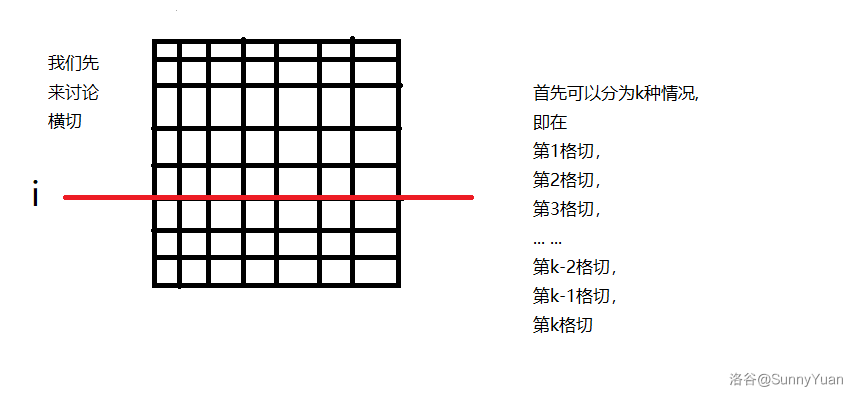
①:考虑选择上面继续割(如下图),丢掉下面的,其分界线为第 \(i\) 行。
所以应该取上面的最优值,同时少割一刀:\(f(x1,y1,i,y2,k-1)\),
而下面的部分为定值:\(\dfrac{(sum-X)^2}{n}\)。
\(sum\) 为下面的部分所有格子的和。
这两个部分合起来就是 \(f(x1,y1,x2,y2,k)\)。

②:考虑选择下面继续割(如上图)。
上面部分的定值:\(\dfrac{(sum-X)^2}{n}\)。
下面的最优值:\(f(i+1,y1,x2,y2,k-1)\)。
\(sum\) 为上面的部分所有格子的和。
下面考虑纵切。
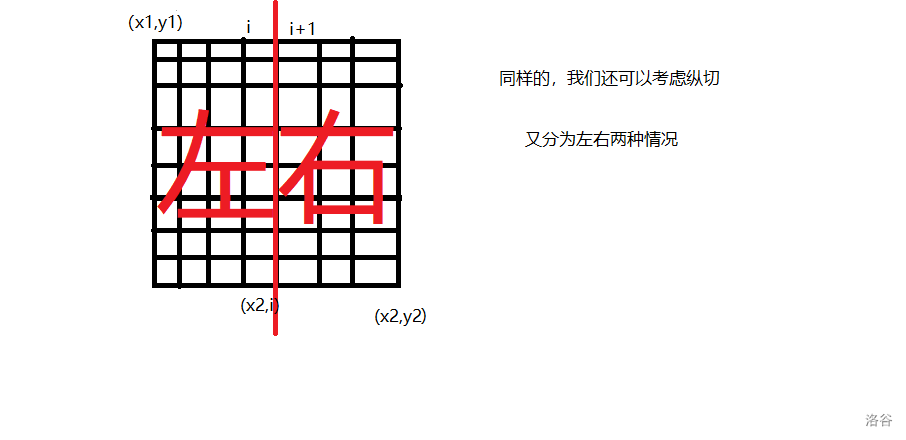
③:考虑选择左边继续割(如上图),分界线为第 \(i\) 列。
取左边的最优值:\(f(x1,y1,x2,i,k-1)\),
右边的部分为定值:\(\dfrac{(sum-X)^2}{n}\)。
\(sum\) 为右边的部分所有格子的和。
④:考虑选择右边继续割(如上图)。
取右边的最优值:\(f(x1,i+1,x2,y2,k-1)\),
左边的部分为定值:\((sum-X)\times(sum-X)/n\),
\(sum\) 为左边的部分所有格子的和。
我们每次取一个值,其实都是在将问题规模缩小。
情况考虑清楚了,那怎么从一个 \(f\) 到另一个 \(f\) 呢,如果是用普通的区间 DP,那估计要使用 \(5\) 层甚至更多的循环,所以,我们使用万能的记忆化搜索,免去繁琐的循环结构。
综上所述,
我们便实现了对大区间的拆分。
而我们不断提到 \(sum\),是一块区域的和,那么,我们可以使用二维前缀和来维护。相信大家一定会。
好了,上 AC 代码。
#include <bits/stdc++.h>
using namespace std;
const int N=15;
const double INF=1e10; //因为要求min,所以要定义INF
int n;
int m=8;
double X; //平均值
double s[N][N]; //记录每个格子的值
double f[N][N][N][N][N]; //状态
double GetSum(int x1,int y1,int x2,int y2)//求[x1,y1]~[x2,y2]的和,为下文的GetX服务
{
return s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1];
}
double GetX(int x1,int y1,int x2,int y2)// 计算上文的(sum−X)×(sum−X)/n。
{
return (GetSum(x1,y1,x2,y2)-X)*(GetSum(x1,y1,x2,y2)-X)/n;
}
double DFS(int x1,int y1,int x2,int y2,int k)//使用记忆化搜索进行递归调用
{
double& v=f[x1][y1][x2][y2][k];//因为太难写了,所以给f[x1][y1][x2][y2][k]建立引用
if(v>=0)return v; //已经访问过该点了,直接返回
if(k==1)return v=GetX(x1,y1,x2,y2);//最后一块,不可能再割了
v=INF; //为求最小值做准备
for(int i=x1;i<x2;i++) //下面是刚刚讨论的结果
{
v=min(v,DFS(x1,y1,i,y2,k-1)+GetX(i+1,y1,x2,y2));
v=min(v,DFS(i+1,y1,x2,y2,k-1)+GetX(x1,y1,i,y2));
}
for(int i=y1;i<y2;i++)
{
v=min(v,DFS(x1,y1,x2,i,k-1)+GetX(x1,i+1,x2,y2));
v=min(v,DFS(x1,i+1,x2,y2,k-1)+GetX(x1,y1,x2,i));
}
return v;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=m;i++)
{
for(int j=1;j<=m;j++)
{
double x;
scanf("%lf",&x);
s[i][j]=s[i-1][j]+s[i][j-1]+x-s[i-1][j-1]; //建立前缀和
}
}
X=s[m][m]/n; //求平均值
memset(f,0x80,sizeof f); //初始化
printf("%.3f\n",sqrt(DFS(1,1,m,m,n)));//注意,一定要根号啊啊啊!!!
return 0;
}
CF1728A Colored Balls: Revisited
修改时间:2022/9/11修改了格式与标点
修改时间:2022/9/13修改了个别不严谨的语句
题目大意
有 \(n\) 种颜色的球,颜色为 \(i\) 的球为 \(cnt_i\) 个(\(cnt_1+cnt_2+\dots+cnt_n\) 为奇数)。每次从球堆中取出 \(2\) 个颜色不相同的球,问最后可能剩下哪种颜色的球(输出任意一种即可)。
题目分析
其实只要找出序列中最大值所在位置 \(i\) 即可,那就是最后剩下的一种球。
理论证明(可以不看)
将 \(cnt\) 数组从小到大排序,先同时拿排在第一个位置和第二个位置的球,直到第一个位置没有球了(也就是排序后的第一个颜色被拿完了)。
此时第二个位置应该还有球,再同时拿第二个位置和第三个位置的球,直到第二个位置没有球了。
第三个位置应该还有球。
以此类推,最后在第 \(n-1\) 个位置的球拿完时,第 \(n\) 个位置的球一定是唯一的一种颜色的球。
常见问题
Q1:如果只有两个数字且个数相同怎么办?
A1:那它们的和为偶数违背了题意(\(cnt_1+cnt_2+\dots+cnt_n\) 为奇数)。
Q2:会不会到最后两个位置时,它们的数字相同?
A2:不可能。因为在两个数字的时候不成立(已证明)。那在多个数字的时候,第 \(n-1\) 个数字已经和第 \(n-2\) 个数字消掉一部分了,如果此时 \(cnt_{n-1}=cnt_{n-2}\),那么原先的 \(cnt_{n-1}\) 一定大于 \(cnt_{n-2}\),与排序矛盾。
代码实现
#include <bits/stdc++.h>
using namespace std;
const int N=25; //最大个数为25个
int T,n; //数据组数与数据个数
int a[N]; //存放数字
void solve()
{
int color_max=1; //记录最大值的那一位
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=2;i<=n;i++)
if(a[color_max]<a[i])//如果当前值比最大值还要大,更新最大值
color_max=i;
printf("%d\n",color_max);//输出最大值所在位置
}
int main()
{
scanf("%d",&T);
while(T--)solve();
return 0;
}
CF546E Soldier and Traveling
本文适合初学者阅读。dalao勿喷
对于这种类型的题目,又是增加,又是减少的,我们可以使用网络流进行转化。
说句废话:
网络流这个东西,趣味十足,上可顶替匈牙利算法,下可转化动态规划。它似水一般灵活,总是可以出乎意料地解决问题。
好了,说回来,看到这种题目,你有什么疑惑?
说说我的吧:
信息这么多(\(a_i\) 和 \(b_i\)),怎么保存?
这么多的点,无组织,无纪律,怎么办呢?
这情况也太多了吧,怎么
暴搜思考呢?即使知道可行,这题的输出怎么办呢?
真恶心
我们从网络最大流的角度一个一个来思考吧!
1. 信息这么多,怎么保存?
我们可以把一个点的信息一分为2,让他们整齐罗列。
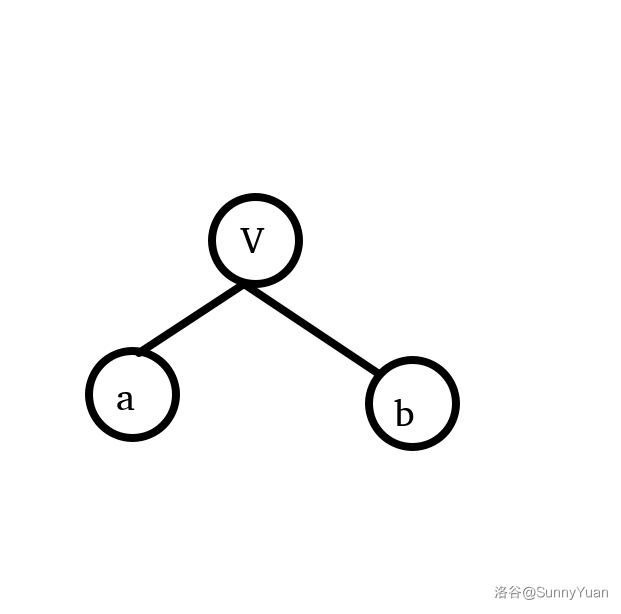
千万不要误以为 \(a_i\) 和 \(b_i\) 为节点,图中只是形象化地阐述“把一个点的信息一分为2”
2. 这么多的点,无组织,无纪律,怎么办呢?
那就找两个领导把他们汇总起来,这两个领导叫做源点以及汇点。
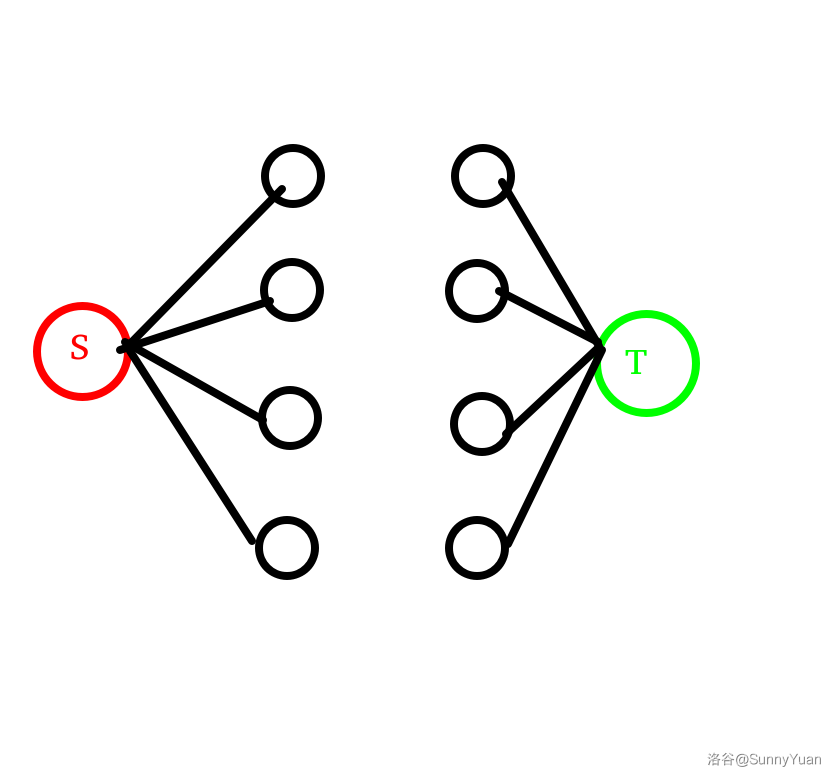
那流量是多少呢?
看图!
看左半部分,点 \(i\) 的流量为 \(a_i\)。
同理,右半部分流量为 \(b_i\)。
中间部分暂不考虑
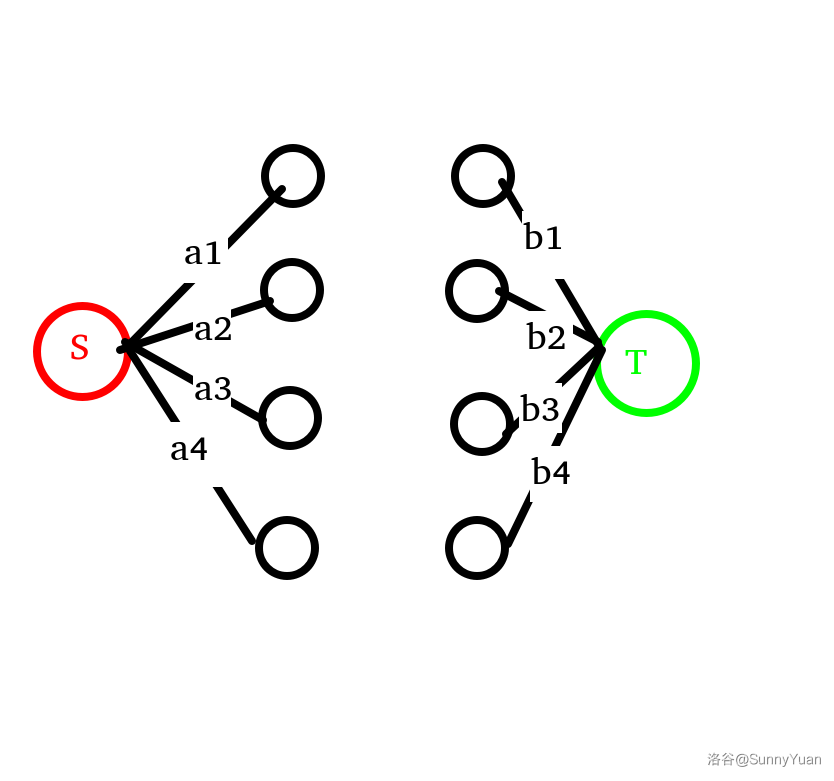
为什么要这样干呢?
现在假设 \(S\) 点有无穷无尽的水资源。
那么可以往每个左边的河道里塞满水,也就是对于左边的点 \(i\)(图中是靠近红点的四个点)的初始值为 \(a_i\)。
也就是对应题目中“每个点初始时有 \(a_i\) 个人”的条件。
同样的道理,经过中间一番乱七八糟的处理后,从右边流出的水应为 \(b_1,b_2,\dots,b_n\),表示最终处理后,对于右边的点 \(i\) (图中是靠近绿点的四个点)最终为 \(b_i\)。
也就是对应题目中“每个点最终有 \(b_i\) 个人”的条件。
3. 这情况也太多了吧,怎么思考呢?
也就是考虑中间部分。
首先,有些人可以选择留下。那么对于这些点的水,随它们流,连接 \(n\) 条边,流量为 \(+\infin\)。
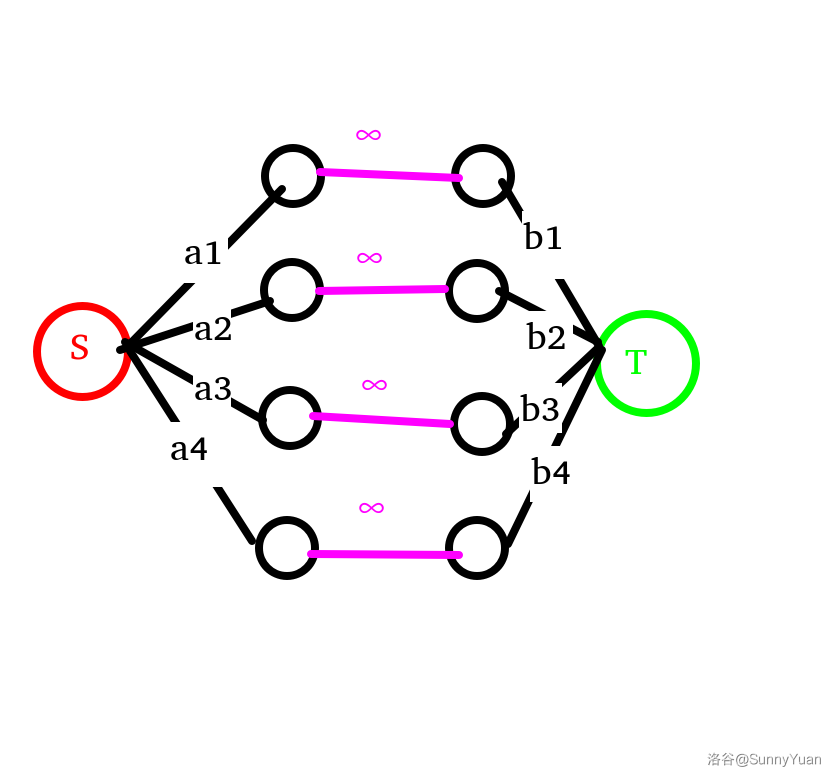
当然,如果有边相连,那也随便流,连接 \(m\) 条边(与题目中的 \(m\) 意义相同),如图(假设有这些边)。
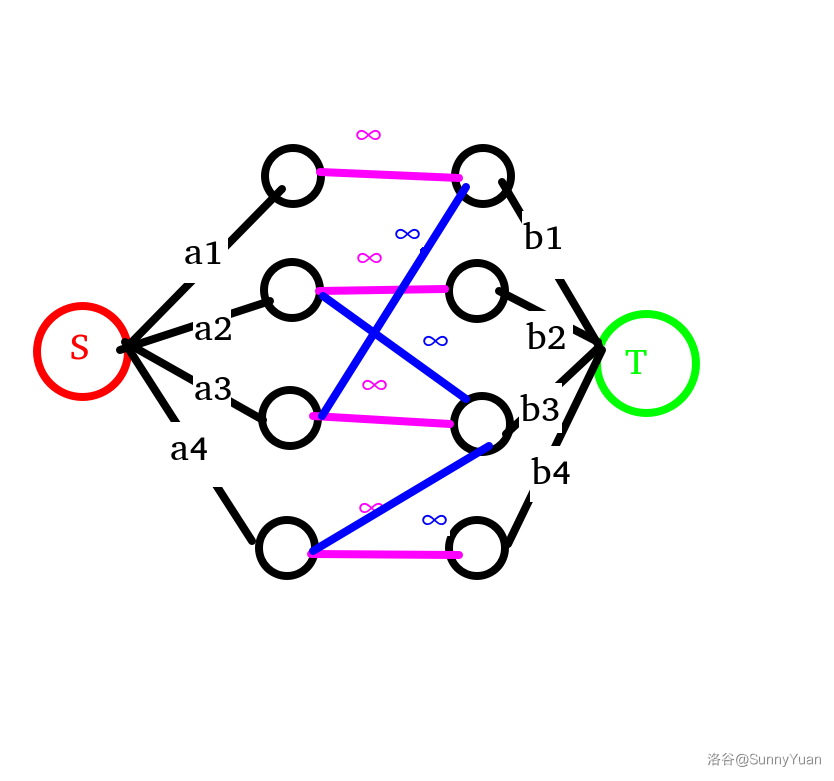
于是乎,跑一遍Dinic算法足矣!
- 即使知道可行,这题的输出怎么办呢?
真恶心
众所周知,Dinic会在找到增广路时,建立反边,以便反悔。
那么这些反边,就是我们利用的对象。
一条边的反边的权值不就是流过该边的流量吗?

把中间部分的每条反边揪出来,在保存到一个数组里即可。
AC Code
#include <iostream>
#include <cstring>
#include <algorithm>
#include <numeric>
const int N = 210, M = 1410, INF = 1e9;
struct Node
{
int to;
int next;
int w;
}e[M];
int head[N], cur[N], idx = 1;
void add(int a, int b, int c) // 加边
{
idx++;
e[idx].to = b;
e[idx].next = head[a];
e[idx].w = c;
head[a] = idx;
idx++;
e[idx].to = a;
e[idx].next = head[b];
e[idx].w = 0;
head[b] = idx;
}
int n, m;
int a[N];
int b[N];
int S, T;
int sum1, sum2; // sum1:a sum2:b
int d[N];
bool bfs()
{
static int q[N]; // 队列
int hh = 0, tt = 0;
memset(d, 0, sizeof(d));
q[0] = S;
cur[S] = head[S];
d[S] = 1;
while (hh <= tt)
{
int t = q[hh++];
for (int i = head[t]; i; i = e[i].next)
{
int to = e[i].to;
if (!d[to] && e[i].w)
{
cur[to] = head[to];
d[to] = d[t] + 1;
q[++tt] = to;
if (to == T) return true;
}
}
}
return false;
}
int dinic(int u, int limit)
{
if (u == T) return limit;
int rest = limit;
for (int i = cur[u]; i && rest; i = e[i].next)
{
cur[u] = i;
int to = e[i].to;
if (d[to] == d[u] + 1 && e[i].w)
{
int k = dinic(to, std::min(rest, e[i].w));
if (!k) d[to] = 0;
rest -= k;
e[i].w -= k;
e[i ^ 1].w += k;
}
}
return limit - rest;
}
int map[N][N]; // 记录反边信息,即结果
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin >> n >> m;
for (int i = 1; i <= n; i++)std::cin >> a[i];
for (int i = 1; i <= n; i++)std::cin >> b[i];
sum1 = std::accumulate(a + 1, a + n + 1, 0); // 求和
sum2 = std::accumulate(b + 1, b + n + 1, 0);
if(sum1 != sum2) //直接排除
{
std::cout << "NO" << '\n';
return 0;
}
for (int i = 1; i <= n; i++) add(0, i, a[i]); // 左
for (int i = n + 1; i <= n * 2; i++) add(i, n * 2 + 1, b[i - n]); // 右
for (int i = 1; i <= n; i++) add(i, i + n, INF); // 中1
for (int i = 1; i <= m; i++) // 中2
{
int a, b;
std::cin >> a >> b;
add(a, b + n, INF);
add(b, a + n, INF);
}
S = 0, T = n * 2 + 1;
auto query = [&]() // Dinic 模板
{
int maxflow = 0, flow = 0;
while (bfs())
{
while (flow = dinic(S, INF))
{
maxflow += flow;
}
}
return maxflow;
};
if (query() != sum1) // 直接排除
{
std::cout << "NO" << '\n';
return 0;
}
else // 扣反边
{
std::cout << "YES" << '\n';
int t = 4 * n + 2;
for (int i = 1; i <= 2 * m + n; i++)
{
map[e[t ^ 1].to][e[t].to - n] += e[t ^ 1].w; // 注意要 -n
t += 2;
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
std::cout << map[i][j] << ' ';
}
std::cout << '\n';
}
}
return 0;
}
Atcoder ABC244E - King Bombee
原题:
题意
给你一张图,从 \(S\) 到 \(T\),经过 \(k\) 条边, 经过 \(X\) 号点偶数次的方案数。
做法
设 \(f_{i, j, k}\) 表示经过 \(i\) 条边,现在在 \(j\),经过 \(X\) 的次数的奇偶。
初始状态:
\(f_{0, S, 0} = 1\)
状态转移:
\(f_{i, u, k} = \sum_{(u, v) \in E}f_{i - 1, v, k}(u \ne X)\)
\(f_{i, u, k} = \sum_{(u, v) \in E}f_{i - 1, v, 1 - k}(u = X)\)
即如果当前节点为 \(X\),那么从上一个节点到这个节点需要改变奇偶(因为到达 \(X\) 的点数会 \(+ 1\) 所以会改变奇偶性。
对应:
\(f_{i, u, k} = \sum_{(u, v) \in E}f_{i - 1, v, 1 - k}(u = X)\)
如果当前节点不为 \(X\),那么奇偶性不会变。
对应:
\(f_{i, u, k} = \sum_{(u, v) \in E}f_{i - 1, v, k}(u \ne X)\)
C++ 代码
记录:戳这里
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2010, M = 4010, mod = 998244353;
struct Edge {
int to;
int next;
}e[M];
int head[N], idx;
void add(int a, int b) {
idx++;
e[idx].to = b;
e[idx].next = head[a];
head[a] = idx;
}
int f[N][N][2];
int n, m, k, s, t, x;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m >> k >> s >> t >> x;
for (int i = 1; i <= m; i++) {
int u, v;
cin >> u >> v;
add(u, v);
add(v, u);
}
f[0][s][0] = 1;
for (int i = 1; i <= k; i++) {
for (int j = 1; j <= n; j++) {
for (int l = head[j]; l; l = e[l].next) {
int to = e[l].to;
for (int r = 0; r <= 1; r++) {
if (j == x) f[i][j][r] = (f[i][j][r] + f[i - 1][to][1 - r]) % mod;
else f[i][j][r] = (f[i][j][r] + f[i - 1][to][r]) % mod;
}
}
}
}
cout << f[k][t][0] << '\n';
return 0;
}
CF1799B Equalize by Divide
本蒟蒻学习了jiangly大佬的思想,来发一个题解。
大致题意:
给定一个 \(n\) 个元素的数组 \(a\),每次可以选择 \(a[i]\) 和 \(a[j]\),然后使 \(a[i] = \lceil \frac{a_i}{a_j} \rceil\),如果最后可以使数组中的所有元素都相等,那么输出
Yes,并输出每一个操作\(i, j\);否则输出No。
本人不擅长使用Markdown,详细思路写在代码里面了。
// 思路:
// 1. 如果所有数字都相等,那么什么也不用干。
// 接下来的所有判断都假定所有数字不相等
// 2. 如果数组中有1,一定不可行,因为任何数字除以它还是它自己,用1除以任何数字却还是1,所以数组中有了1,就妄图改变数组中的任何一个数字。
// 3. 固定a[1], 不断地用别的数字a[i]和a[1]如以下方式操作,直到整个数组变为a[1]或者出现了2。
// 3. 1. 如果a[1] < a[i],那么a[1] = a[1] / a[i] 上取整。
// 3. 2. 否则,a[i] = a[i] / a[1] 上取整。
// 4. 如果,整个数组变为a[1],直接输出当前处理的步骤。
// 5. 否则,就将数组中不是2的元素,一个一个与2进行操作,再输出所有步骤。
// C++新语法:
// count(a, b, c) (a, b)的区间内c的个数
// find(a, b, c) 在(a, b)区间内找c并返回其指针
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
using PII = pair<int, int>;
const int N = 110;
int n;
int a[N];
PII ans[N * 35];
int cnt;
void solve() {
cnt = 0;
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
if (count(a + 1, a + n + 1, a[1]) == n) {
cout << 0 << '\n';
return;
}
if (count(a + 1, a + n + 1, 1) >= 1) {
cout << -1 << '\n';
return;
}
while (count(a + 1, a + n + 1, a[1]) < n && count(a + 1, a + n + 1, 2) == 0) {
int pos = 2;
while (a[pos] == a[1]) {
pos++;
}
if (a[pos] > a[1]) {
if (a[pos] % a[1]) a[pos] = a[pos] / a[1] + 1;
else a[pos] = a[pos] / a[1];
ans[++cnt] = {pos, 1};
}
else {
if (a[1] % a[pos]) a[1] = a[1] / a[pos] + 1;
else a[1] = a[1] / a[pos];
ans[++cnt] = {1, pos};
}
}
if (count(a + 1, a + n + 1, a[1]) < n) {
int pos2 = find(a + 1, a + n + 1, 2) - a;
for (int i = 1; i <= n; i++) {
while (a[i] != 2) {
if (a[i] & 1) a[i] = a[i] / 2 + 1;
else a[i] = a[i] / 2;
ans[++cnt] = {i, pos2};
}
}
}
cout << cnt << '\n';
for (int i = 1; i <= cnt; i++) cout << ans[i].first << ' ' << ans[i].second << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) solve();
return 0;
}
CF1654E Arithmetic Operations
题目让我们求改变数字的最少次数,那我们转化一下,
求可以保留最多的数字个数 \(cnt\),再用 \(n\) 减一下就行,即 \(res = n - cnt\)。
我们先考虑两种暴力方法。
第一种暴力方法:
大体思路:因为要保留的最多,那么我们肯定要在众多等差数列中找能对应数字最多的那一个并保留下来。
首先,我们要知道一个概念。

对于这道题,那么我们可以暴力枚举公差 \(d\)(就是数组中相邻两项的差值都是 \(d\),并把题目中的每个 \(a[i]\) 对应的等差数列的最后一项 \(a[i] + d \times (n - i)\) 计算出来。
对于同一个公差 \(d\),如果不同位置计算出来的序列的最后一个值相同,那就说明它们属于同一个等差数列。

如果有 \(x\) 个数字计算出来的最后一个值都相同,那么采用其对应的等差数列作为修改后的数组,这 \(x\) 个数字是不需要改变的,只需要改变 \(n - x\) 个数字。
那我们可以想到,用桶记录计算出来的值 \(x\) 的出现次数 \(a[x]\)。如果某一次计算出来的值为 \(x\),那么可以将 \(a[x]\) 加 \(1\)。
如果 \(a[x]\) 是 \(a\) 中最大的元素,那么说明,以 \(a[x]\) 为结尾的等差数列中存在的元素数量最多,那么更改数字的数量也就减少了,只需要 \(n - a[x]\) 个元素。
这种方法的时间复杂度为 \(O(DN)\),\(D\) 为需要枚举的公差数量。
第二种暴力方法:
考虑动态规划,设 \(f[i][j]\) 表示以 \(a[i]\) 为等差数列最后一个元素的以 \(j\) 为公差的等差数列最多可以保留的数字个数。
我们可以枚举上一个数字 \(a[k]\),如果它与 \(a[i]\) 在同一等差数列,那么有 \(f[i][j] = f[k][j] + 1\),表示又可以多保存一个数字了。
那这个序列的公差是多少呢?
这样考虑,中间有 \(i - k\) 个公差,差了 \(a[i] - a[k]\),那么公差就是\(\frac{a[i] - a[k]}{i - k}\)。
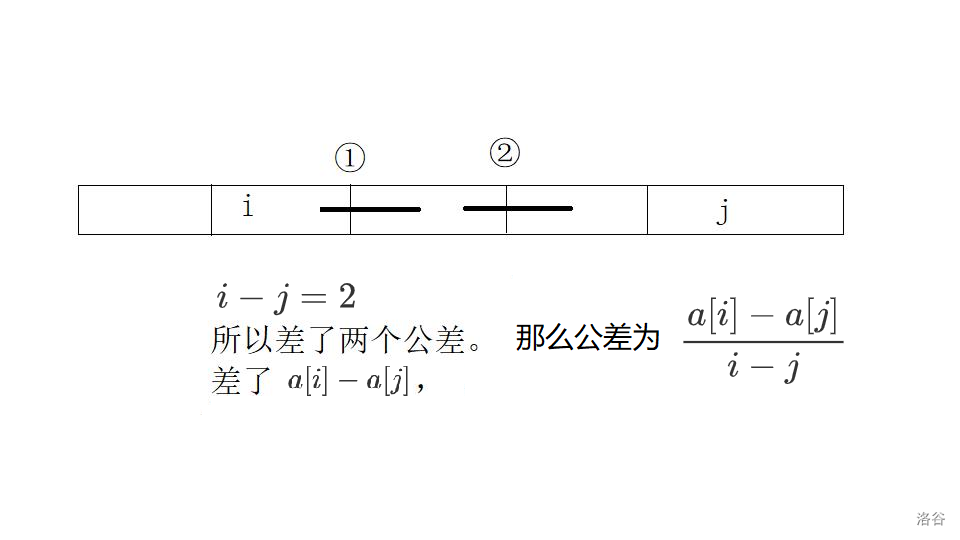
如果除不尽怎么办呢,那么这就说明 \(a[i]\) 和 \(a[k]\) 不能在同一个等差数列,不然公差为小数!
那 \(k\) 从哪里开始枚举呢?从 \(1\) 开始是不是太慢了?
这个等会儿讲。
那么为了平衡这两种暴力算法,我们可以这样办:
取输入的数列 \(a\) 的最大值 \(m\)。
我们只使用第一种方法枚举 \([0, \sqrt m]\) 的部分,时间复杂度为 \(O(n \sqrt m)\)。
我们使用第二种方法枚举 \([\sqrt m + 1, n]\) 的部分。
下面探讨第二种方法的时间复杂度,
首先回归到前面的问题,来探讨 \(k\)(\(i\) 的上一位数字在哪里) 从何处开始枚举,到哪里。
到哪里好解决,就是 \(i - 1\)。
而开始的地方,是 \(i - \sqrt m\)。为啥呢?
首先,因为公差 \(D\) 在 \([\sqrt m + 1, n]\) 之间,所以 \(D > \sqrt m\),那么我们计算差值 \(a[i] - a[k] = (a[k] + (i - k) \times D) - a[k] = (i - k) \times D > (i - k) \times \sqrt m\)。
首先假设 \(i, k\) 都在同一个等差数列中,如果 \(k+ \sqrt m < i\),那么\(a[i] - a[k] > (i - k) \times \sqrt m > \sqrt m \times \sqrt m = m\),这样的话,两数之差竟然比 \(m\) 还要大,不成立,
所以 \(k + \sqrt m \geq i\),也就是说 \(k\) 要从 \(i - \sqrt m\) 开始枚举。
所以,第二种方法的时间复杂度为 \(O(n \sqrt m)\)。
那么这个题的时间复杂度就为 \(O(n \sqrt m)\)。
代码:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <unordered_map>
using namespace std;
const int N = 100010;
int n;
int a[N], maxx, sqrtmaxx;
int u[(int)(N + N * sqrt(N))]; // 第一种暴力方法的桶
unordered_map<int, int> f[N]; // 第二种暴力方法的动态规划数组。
int max_keep() {
int ans = 0;
for (int d = 0; d <= sqrtmaxx; d++) { // 第一种暴力方法,枚举公差 D
for (int i = 1; i <= n; i++) {
ans = max(ans, ++u[a[i] + (n - i) * d]);
}
for (int i = 1; i <= n; i++) {
u[a[i] + (n - i) * d]--;
}
}
for (int i = 1; i <= n; i++) { // 第二种暴力方法,动态规划
for (int j = max(1, i - sqrtmaxx); j < i; j++) {// j只用从 i - sqrt(m) 开始枚举
if ((a[i] - a[j]) % (i - j) == 0) {
int x = (a[i] - a[j]) / (i - j);
if (x <= sqrtmaxx) continue;
f[i][x] = max(f[i][x], f[j][x] + 1);
ans = max(f[i][x] + 1, ans);
}
}
}
for (int i = 1; i <= n; i++) f[i].clear(); // 清空数组
return ans;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i], maxx = max(maxx, a[i]);
sqrtmaxx = sqrt(maxx);
int ans1 = 0, ans2 = 0;
ans1 = max_keep();
reverse(a + 1, a + n + 1); // 应对公差为负数的情况
ans2 = max_keep();
cout << n - max(ans1, ans2) << '\n';
return 0;
}
P3574 [POI2014] FAR-FarmCraft
洛谷上面的题解写的真的不太好,有很多错误,我来谈谈自己的理解。
设 \(f[i]\) 表示以 \(i\) 为根节点的子树中(包括节点 \(i\))的所有人安装好游戏所需要的时间(与下面的 \(g[i]\) 并没有包含关系,管理员也没有强制性要求要回到根节点,比如会出现下图情况)。
设 \(g[i]\) 表示从 \(i\) 开始往下走,兜一圈又回到 \(i\) 所需要的时间。
实际上 \(f[i]\) 可能 \(< g[i]\),比如当出现如下情况的时候:
假设下图中所有人的安装时间为 \(1\),
那么当管理员兜了一个圈,第二次到达 \(3\) 的时候,
所有人都已经安装完成了。
所以在此图中 \(f[1] < g[1]\)。
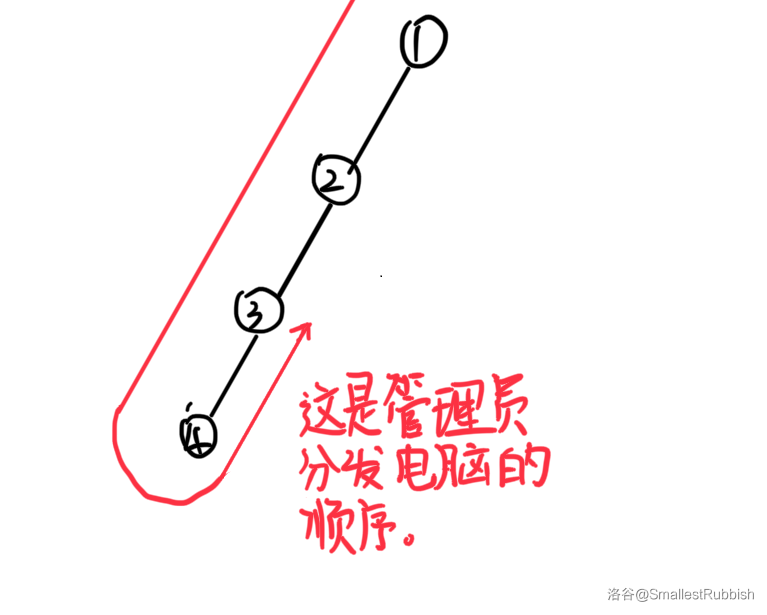
那我们先访问那个节点呢?
分为两种情况考虑,即 \(f[i] - g[i] \geq 0\) 和 \(f[i] - g[i] < 0\) 两种情况。
如果管理员回到了起点那些人还没有装完(即 \(f[i] - g[i] \geq 0\)),那么就需要等待 \(f[i] - g[i]\) 的时间所有人才能安装好。
根据常识,在等待的这段时间我们可以去下一家,以减少所需的总时间。
这里我们利用贪心,让需要等待时间最久的作为第一个访问的节点,
这样可以管理员在他漫长的安装时间内将电脑送给其他人。
而如果出现了像上图一样的情况(即 \(f[i] - g[i] < 0\)) 的情况,
根本就不需要等待,
也就不用排序,
随机访问即可,
但为了简单起见,
排了序也没有什么问题。
所以我们可以对 \(f[i] - g[i]\) 从大到小进行排序。
再挨个访问即可。
然后就是利用 \(f\) 和 \(g\) 来用子树信息更新父亲节点。
如下图:

先说结论:只安装到 \(i\) 点会需要 \(\sum (g[j] + 2) + 1 + f[i]\) 的时间能完成安装,其中 \(j\) 为比 \(i\) 先遍历到的同一层的节点(如上图)。
为什么是这样呢?
第一部分的 \(\sum (g[j] + 2)\) 表示遍历完所有 \(j\) 子树的节点,每次都回到根节点(所以要 \(+2\))。
第二部分的 \(+1\) 表示从根节点走到 \(i\) 所需要的步骤(即为 \(1\) 步)。
最后一部分的 \(f[i]\) 表示把 \(i\) 子树内所有的游戏装好了需要花的时间。
总时间取 \(\max\) 即可, 即 \(f[root] = \max\{\sum (g[j] + 2) + f[i] + 1\}\)。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 500010;
struct Edge {
int to, next;
}e[N * 2];
int head[N], idx;
void add(int a, int b) {
idx++;
e[idx].to = b;
e[idx].next = head[a];
head[a] = idx;
}
int n, t[N];
int f[N], g[N];
void dfs(int u, int fa) {
vector<int> wait;
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (to == fa) continue;
dfs(to, u);
wait.push_back(to);
}
sort(wait.begin(), wait.end(), [](const int& a, const int& b) { return f[a] - g[a] > f[b] - g[b]; });
for (int i = 0; i < wait.size(); i++) {
f[u] = max(f[u], g[u] + 1 + f[wait[i]]);
g[u] += g[wait[i]] + 2;
}
if (t[u] > g[u] && u != 1) f[u] = max(f[u], t[u]);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) cin >> t[i];
for (int i = 1; i < n; i++) {
int a, b;
cin >> a >> b;
add(a, b);
add(b, a);
}
dfs(1, 0);
cout << max(f[1], g[1] + t[1]) << '\n';
return 0;
}
P3755 [CQOI2017]老C的任务
如果询问 \(x_1, y_1, x_2, y_2\),
那么询问
\((x_2, y_2)\),
\((x_2, y_1 - 1)\),
\((x_1 - 1, y_2)\)
\((x_1 - 1, y_1 - 1\)),
这些点到原点(不一定是 \((0, 0)\),有可能有负数)的和。
设其结果分别为 \(a, b, c, d\),那么最后结果为 \(a - b - c + d\)(二维前缀和原理)。
问题成功转化。
设结构体
struct Node {
int x, y; // 位置
int z; // 值
};
为基本信息。
我们在此基础上加一个 \(type\) 和 \(res\),
如果 \(type\) 为 \(1\) 就表示要询问 \((x, y)\) 的二维前缀和,结果保存在 \(res\) 中。
如果 \(type\) 为 \(0\) 表示 \((x, y)\) 为一个基站,其功率为 \(z\)。
对于 \(type_i\) 为 \(1\) 的部分,
使用 CDQ 分治统计:
\(type_j < type_i\) (即 \(type_j\) 为 \(0\))
\(x_j \leq x_i\)
\(y_j \leq y_i\)
的各个位置的和即可。
注意开long long。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#define int long long
using namespace std;
const int N = 500010;
struct Node {
int x, y, z;
int type;
int res;
}a[N], tmp[N];
bool cmp(const Node a, const Node b) {
if (a.x != b.x) return a.x < b.x;
if (a.y != b.y) return a.y < b.y;
return a.type < b.type;
}
int n, m;
void cdq(int l, int r) {
if (l == r) return;
int mid = (l + r) / 2;
cdq(l, mid);
cdq(mid + 1, r);
int sum = 0;
int p = l, q = mid + 1, tot = l;
while (p <= mid && q <= r) {
if (a[p].y <= a[q].y) {
if (!a[p].type) sum += a[p].z;
tmp[tot++] = a[p++];
}
else {
if (a[q].type) a[q].res += sum;
tmp[tot++] = a[q++];
}
}
while (p <= mid) {
if (!a[p].type) sum += a[p].z;
tmp[tot++] = a[p++];
}
while (q <= r) {
if (a[q].type) a[q].res += sum;
tmp[tot++] = a[q++];
}
for (int i = l; i <= r; i++) a[i] = tmp[i];
}
struct Query {
int x1, y1;
int x2, y2;
}query[N];
unordered_map<int, unordered_map<int, int> > res_a;
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> a[i].x >> a[i].y >> a[i].z;
a[i].type = 0;
a[i].res = 0;
}
int tot = n;
for (int i = 1; i <= m; i++) {
cin >> query[i].x1 >> query[i].y1 >> query[i].x2 >> query[i].y2;
a[++tot] = {query[i].x1 - 1, query[i].y1 - 1, 0, 1, 0};
a[++tot] = {query[i].x2, query[i].y2, 0, 1, 0};
a[++tot] = {query[i].x2, query[i].y1 - 1, 0, 1, 0};
a[++tot] = {query[i].x1 - 1, query[i].y2, 0, 1, 0};
}
sort(a + 1, a + tot + 1, cmp);
cdq(1, tot);
for (int i = 1; i <= tot; i++) {
if (a[i].type) {
res_a[a[i].x][a[i].y] = a[i].res;
}
}
for (int i = 1; i <= m; i++) {
int x1 = query[i].x1, y1 = query[i].y1;
int x2 = query[i].x2, y2 = query[i].y2;
int ans = res_a[x2][y2] - res_a[x2][y1 - 1] - res_a[x1 - 1][y2] + res_a[x1 - 1][y1 - 1];
cout << ans << '\n';
}
return 0;
}
CF1810D Climbing the Tree
原题:

思路:
经典的小学数学奥数题。
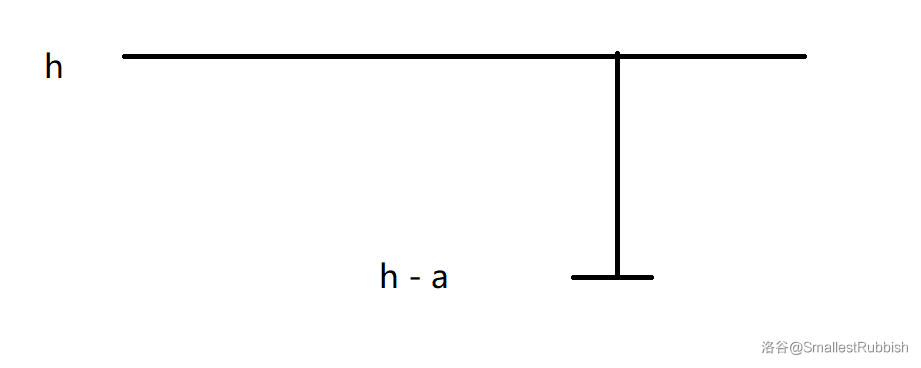
设 \(a\) 为每天往上爬的高度,\(b\) 为每天向下降的高度,\(n\) 为给定的需要爬上去的天数。
请注意,第 \(n\) 天爬上去了,就不会下降了。
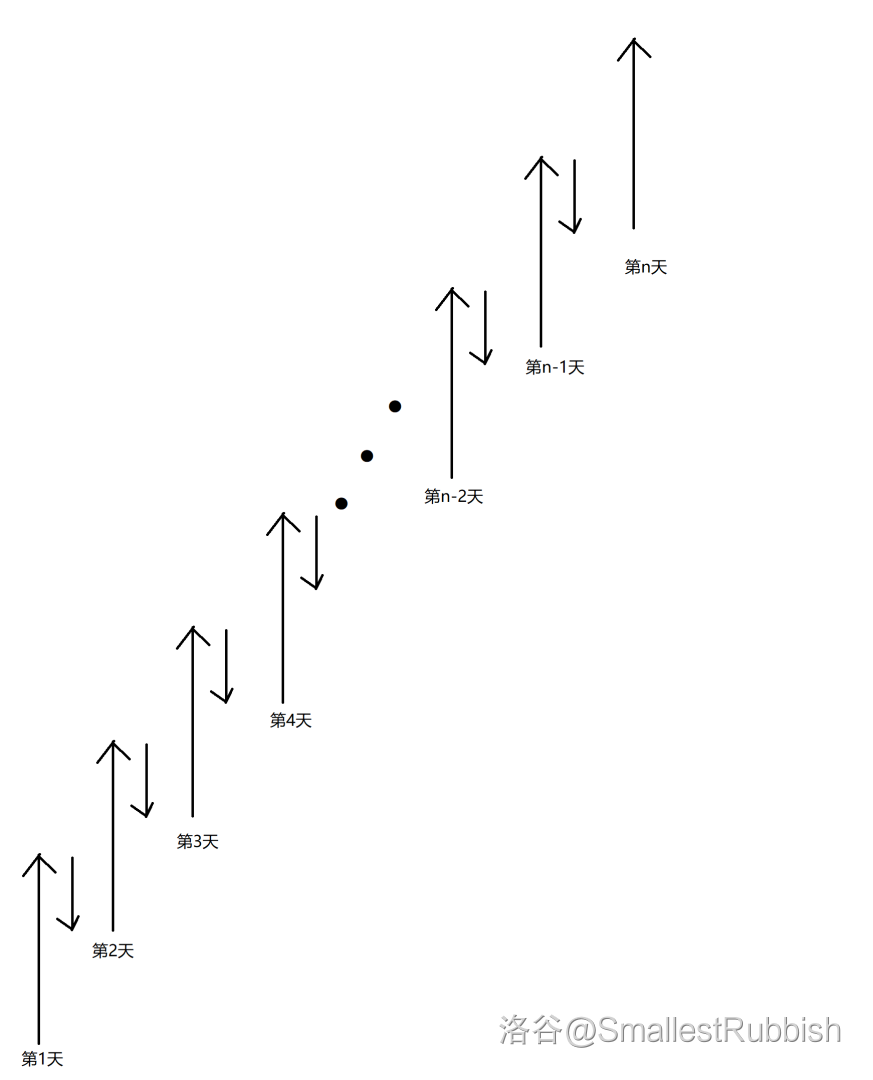
对于操作为 \(1\) 的,我们可以确定其范围。
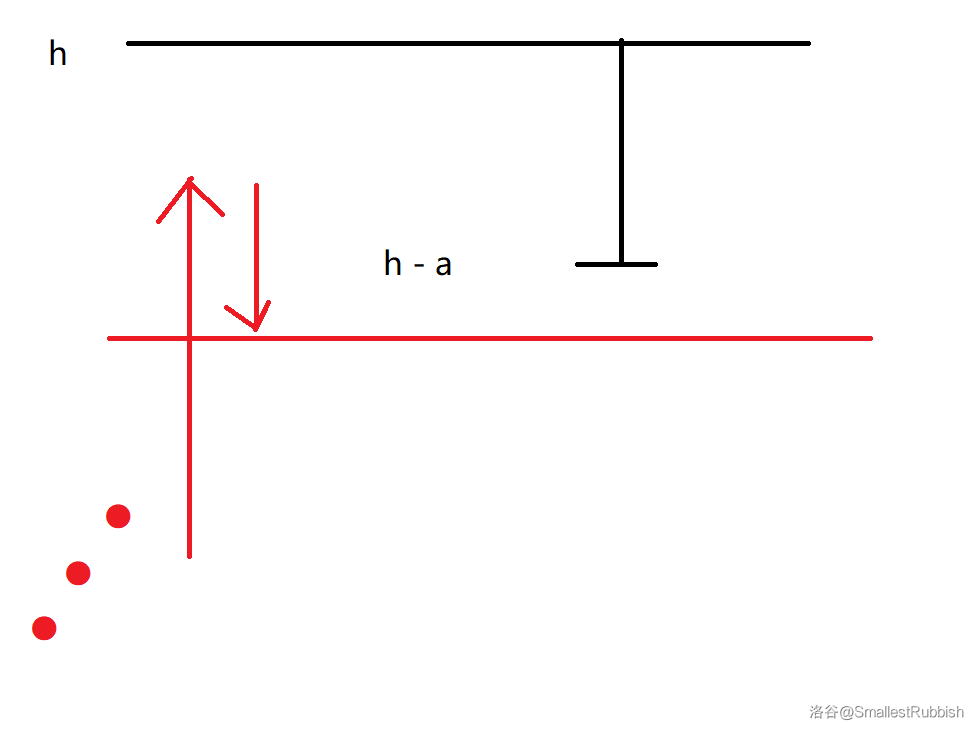
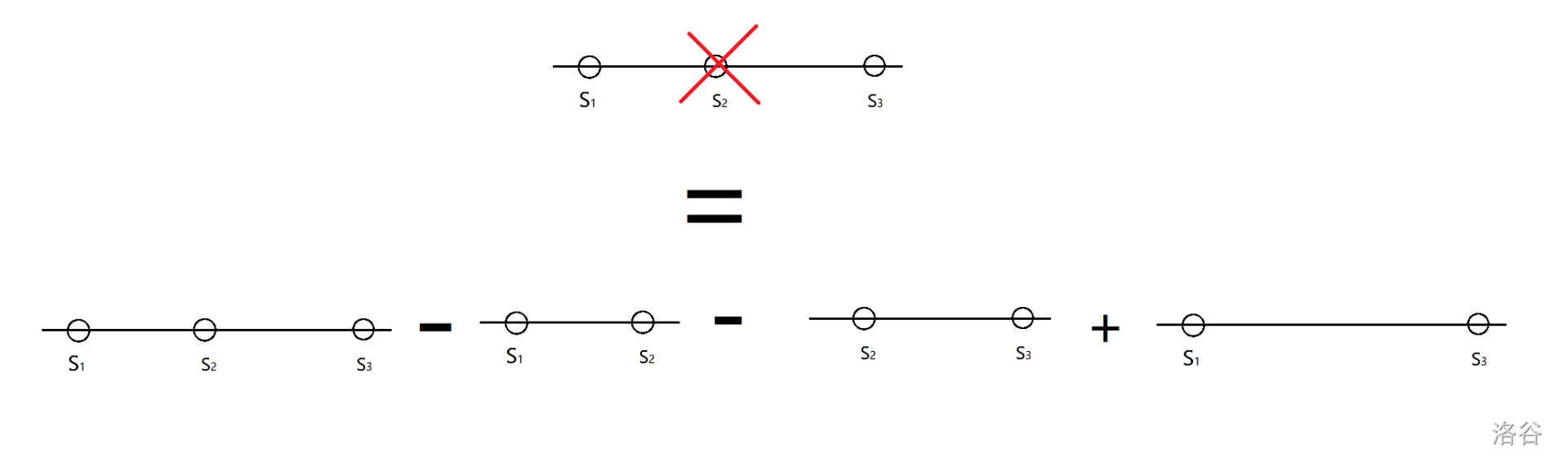
因为要保证第 \(n\) 天就可以到达,且第 \(n - 1\) 天不能到达,所以其范围为标红部分:
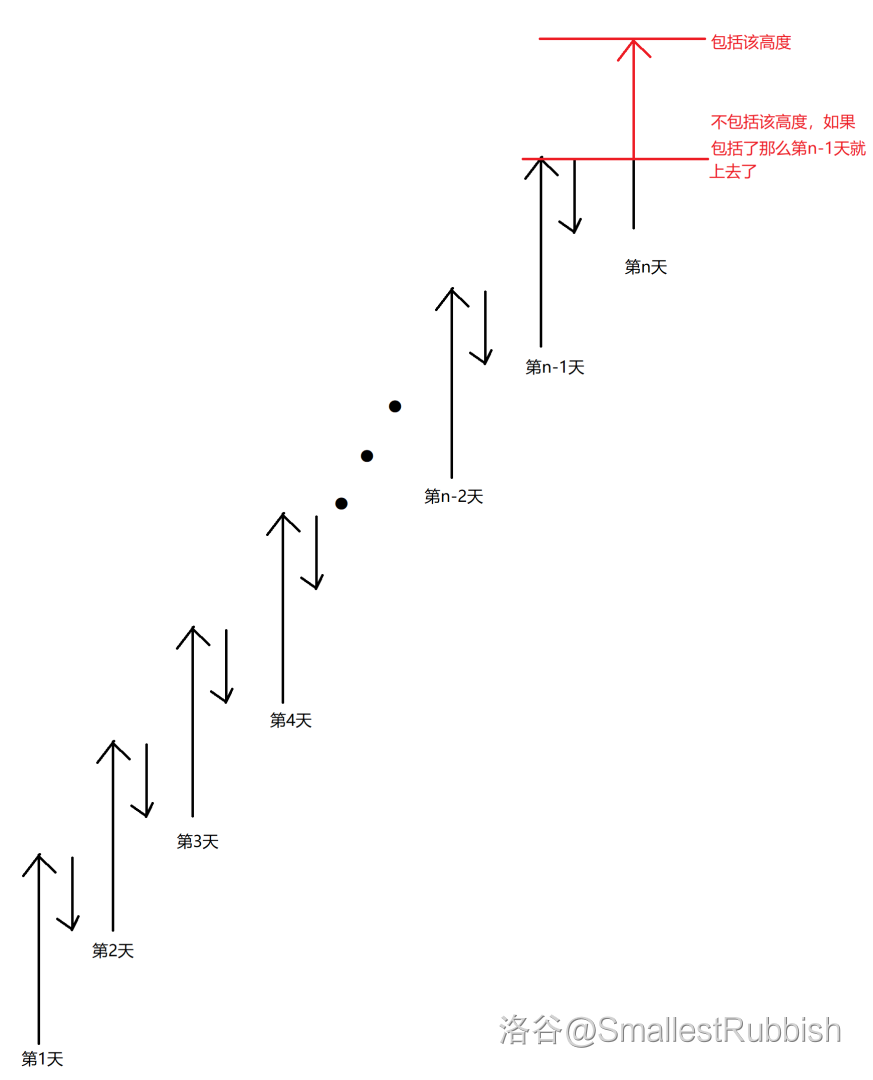
用表达式表示为 \([(a - b) \times (n - 2) + a + 1, (a - b) \times (n - 1) + a]\),其中 \((a - b) \times (n - 2) + a\) 为第 \(n - 1\) 天可以到达的最大高度 \(+1\) 才可以符合题意;\((a - b) \times (n - 1) + a\) 为第 \(n\) 天可以到达的最大高度。
需要特判 \(n = 1\) 的情况,此时其范围为 \([1, a]\)。
如果这个区间与之前之前计算的结果有交集,那么就是可以保留的,并更新区间,否则就丢弃之。
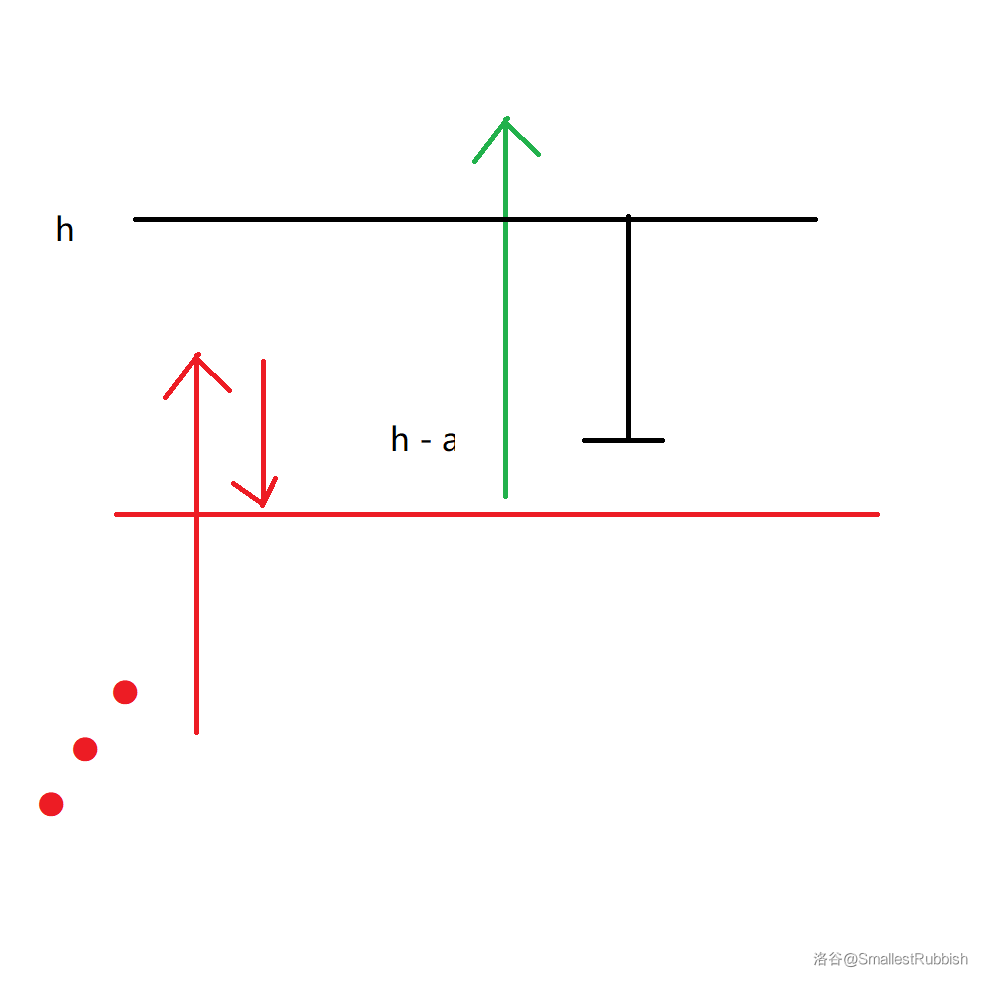
对于操作类型为 \(2\) 的,我们先计算出爬上 \(l\) 的高度需要的时间 \(t\),计算方法如下。
假设高度为 \(h\)。
- 首先要预留一个 \(a\)。
- 然后计算 \(\left\lfloor\frac{h - a}{a - b}\right\rfloor\) 表示到达小于等于 \(h - a\) 的位置所需要的时间。
- 如果刚好到达 \(h - a\) 的位置 \(+1\) 就可以了,否则 \(+2\)。
注意最好不要直接上取整,因为容易引起精度问题。
这样就计算出了 \(t\),然后计算出花 \(t + 1\) 天爬上的高度范围是否与已知范围 \([l, r]\) 有交集,计算方法与前面的操作 \(1\) 类似,如果有那么证明不能准确获取其天数,输出 \(-1\),否则输出天数。
注意我们不能直接判断已知范围 \(l\) 是否等于 \(r\),因为有可能对于这一组询问在该区间内只有一种可能性,也是满足题意的。
代码:
#include <bits/stdc++.h>
#define int long long
using namespace std;
bool check(int& l1, int& r1, int l2, int r2, bool flag) {
int ll = max(l1, l2);
int rr = min(r1, r2);
if (ll > rr) return false;
if (flag) {
l1 = ll;
r1 = rr;
}
return true;
}
void solve() {
int q;
cin >> q;
int opt, a, b, c;
int l = -1, r = 1e18;
while (q--) {
cin >> opt;
if (opt == 1) {
cin >> a >> b >> c;
int lnew = -1, rnew = -1;
if (c == 1) lnew = 1, rnew = a;
else lnew = (a - b) * (c - 2) + a + 1, rnew = (a - b) * (c - 1) + a;
if (check(l, r, lnew, rnew, true)) cout << "1 ";
else cout << "0 ";
}
else {
cin >> a >> b;
int x = l, res = 0;
if (a >= l) {
res = 1;
}
else {
x -= a;
res = x / (a - b);
x = res * (a - b);
if (x == l - a) res++;
else res += 2;
}
c = res + 1;
int lnew = -1, rnew = -1;
if (c == 1) lnew = 1, rnew = a;
else lnew = (a - b) * (c - 2) + a + 1, rnew = (a - b) * (c - 1) + a;
if (check(l, r, lnew, rnew, false)) res = -1;
cout << res << ' ';
}
}
cout << '\n';
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) solve();
return 0;
}
CF371D Vessels
思路:
定义一个权值并查集,权值保存这个集合还可以存下多少水。
如果这个集合可以存放的水已经小于要装入的水,就将这个集合与下一个集合合并。
否则,直接把这个集合可以存放的水减去要装入的水的体积。
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 200010;
int n, m;
int fa[N];
LL g[N], b[N];
int find(int x) {
if (x == fa[x]) return x;
return fa[x] = find(fa[x]);
}
int merge(int x, int y) {
int fx = find(x), fy = find(y);
if (fx == fy) return fx;
fa[fx] = fy;
g[fy] += g[fx];
return fy;
}
void init() {
for (int i = 1; i <= n; i++) fa[i] = i;
}
void modify(int x, LL v) {
x = find(x);
while (true) {
if (g[x] >= v || x >= n) break;
x = merge(x, x + 1);
}
g[x] = max(0ll, g[x] - v);
}
void query(int x) {
int fx = find(x);
if (fx == x) cout << b[x] - g[x] << '\n';
else cout << b[x] << '\n';
}
int main() {
#ifdef DEBUG
freopen("D:/Exercise/Test.in", "r", stdin);
clock_t st, ed;
cout << "===================START===================" << endl;
st = clock();
#endif
cin >> n;
for (int i = 1; i <= n; i++) cin >> g[i], b[i] = g[i];
init();
cin >> m;
int opt, a;
LL b;
for (int i = 1; i <= m; i++) {
cin >> opt;
if (opt == 1) { cin >> a >> b; modify(a, b); }
else { cin >> a; query(a); }
}
#ifdef DEBUG
ed = clock();
cout << "====================END====================" << endl;
cout << "Time:" << (ed - st) * 1.0 / CLOCKS_PER_SEC << " sec" << endl;
#endif
return 0;
}
CF1794B Not Dividing
如果 \(a_i\) 可以整除 \(a_{i - 1}\),只要在 \(a_i\) 上 \(+1\) 即可,这样 \(a_i \bmod a_{i - 1} = 1\) 就满足题目要求了,如果这样算来最多进行 \(n\) 次操作。
但同时要注意 \(a_{i - 1} = 1\) 的情况。如果 \(a_{i - 1}\) 为 \(1\),那么怎么 \(+1\) 都是 \(a_i \bmod a_{i - 1} = 0\) 的。
所以如果当前数字处理完了以后为 \(1\) ,一定要 \(+1\) 变为 \(2\),如此算来最多会进行 \(2n\) 个操作,与题目相符,可以 AC。
/*******************************
| Author: SunnyYuan
| Problem: B. Not Dividing
| Contest: Codeforces Round 856 (Div. 2)
| URL: https://codeforces.com/contest/1794/problem/B
| When: 2023-03-06 08:30:31
|
| Memory: 256 MB
| Time: 2000 ms
*******************************/
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
void solve() {
int n;
cin >> n;
vector<int> a(n);
for (auto& x : a) cin >> x;
if (a[0] == 1) a[0]++;
for (int i = 1; i < a.size(); i++) {
if (a[i] == 1) a[i]++;
if (a[i] % a[i - 1] == 0) {
a[i]++;
}
}
for (auto& x : a) cout << x << ' ';
cout << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) solve();
return 0;
}
CF1794C Scoring Subsequences
文中 \(a\) 为题目中给的 \(a\)。
如果我们要求 \(a_1, a_2, a_3, \dots, a_m\) 的结果,
那么我们可以把 \(a\) 数组从后往前依次除以 \(i\),\(i\) 从 \(1\) 到 \(n\),
即为 \(\frac{a_1}{m},\frac{a_2}{m - 1},\frac{a_3}{m - 2},\dots,\frac{a_{m - 1}}{2},\frac{a_m}{1}\),并将其保存在数组 \(s\) 中。
因为 \(a_1 \leq a_2 \leq a_3 \leq \dots \leq a_m\),且 \(\frac{1}{i}\) 单调递增,所以 \(s_1 \leq s_2 \leq s_3 \dots \leq s_m\)。
那么我们自然而然地可以想到,每一次的结果就是末尾的几个数字的乘积(因为 \(s\) 越大越好),即 \(s_k \times s_{k + 1} \times \dots \times s_m\)。
那么 \(k\) 取多少呢?
我们只取对自己有利的部分,所以当 \(s_k \geq 1\) 且 \(s_{k - 1} < 1\) 时,我们可以达到最大值 \(ans = s_k \times s_{k + 1} \times \dots \times s_m\)。
因为 \(s\) 单调不下降,所以可以使用二分来得出要保留的数字 \(m - k\)。
对每一个 \(m\) 进行操作,\(1 \leq m \leq n\)。
时间复杂度:\(O(n \log n)\)。
C++代码
/*******************************
| Author: SunnyYuan
| Problem: C. Scoring Subsequences
| Contest: Codeforces Round 856 (Div. 2)
| URL: https://codeforc.es/contest/1794/problem/C
| When: 2023-03-06 08:30:32
|
| Memory: 256 MB
| Time: 2500 ms
*******************************/
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 100010;
int n, a[N];
void solve() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++) {
int l = -1, r = i + 1;
while (l + 1 < r) {
int mid = (l + r) / 2;
if (a[i - mid + 1] >= mid) l = mid;
else r = mid;
}
cout << l << ' ';
}
cout << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) solve();
return 0;
}
CF961E Tufurama
-
我们维护一个存储下标数据的树状数组,先将 \(1\sim n\) 插入树状数组。
-
用 \(a\) 表示原数组,\(b\) 表示按照 \(a_i\) 排序后的数组。
-
我们从 \(1\) 开始统计,直到 \(n\),统计时:
-
将 \(i\) 删除,不能把自己算进去。
-
为了排除 \(a_j < i\) 的部分,可以从前往后扫描 \(b\),一直删,直到 \(b_{\text{cur}} \geq i\),
因为 \(b\) 单调不下降,所以 \(i\) 都用不着了, \(i + 1\) 也用不着了。
-
调查 \(a_i \geq j\) 的部分,调用 \(\text{query}(a_i)\) 即可。
-
注意:排除的时候用 \(b\),这样就不用遍历整个 \(a\) 数组来排除 \(a_j < i\) 的部分;
而询问的时候要用 \(a\),因为询问的是 \(a_i \geq j\) 的部分。
-
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
using i64 = long long;
const int N = 200010;
int tr[N];
void add(int x, int v) {
for (; x < N; x += x & -x) tr[x] += v;
}
int ask(int x) {
int res = 0;
for (; x; x -= x & -x) res += tr[x];
return res;
}
int n;
int a[N];
struct Node {
int id;
int v;
}b[N];
bool del[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
b[i].id = i;
b[i].v = a[i];
}
for (int i = 1; i <= n; i++) add(i, 1);
sort(b + 1, b + n + 1, [](const Node& a, const Node& b) { return a.v < b.v; });
int cur = 1;
i64 ans = 0;
for (int i = 1; i <= n; i++) {
if (!del[i]) del[i] ^= 1, add(i, -1);
while (b[cur].v < i && cur <= n) {
if (!del[b[cur].id]) del[b[cur].id] ^= 1, add(b[cur].id, -1);
cur++;
}
ans += ask(min(n, a[i]));
}
cout << ans << '\n';
return 0;
}
CF1580C Train Maintenance
我们以 \(\sqrt m\) 为分界点来进行平衡。
设当前在进行第 \(k\) 次操作,询问 \(i\)。
对于 \(x_i + y_i \leq \sqrt m\),可以在 \(last_{x_i + y_i,day \bmod (x_i + y_i)}\) 上 \(+1\),其中 \(day\) 表示维修的时间,\(k + x_i \leq day \leq k + x_i + y_i - 1\),输出时暴力统计即可。
对于 \(x_i + y_i > \sqrt m\) 的,可以在利用差分数组在 \(f_{day_1}\) 上 \(+ 1\),在 \(f_{day_2}\) 上 \(-1\),其中 \(day_1\) 表示所有的维修时间的开始时间,\(day_2\) 表示所有维修时间的结束时间的后面一天。
时间复杂度:\(O(m\sqrt m)\)。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 200010, V = 450;
int n, m, s;
int st[N];
int f[N];
int last[V][V];
int x[N], y[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
s = sqrt(m);
for (int i = 1; i <= n; i++) cin >> x[i] >> y[i];
int opt, a;
int sum = 0;
for (int i = 1; i <= m; i++) {
cin >> opt >> a;
if (opt == 1) {
if (x[a] + y[a] > s) {
for (int j = i + x[a]; j <= m; j += x[a] + y[a]) {
f[j] += 1;
if (j + y[a] <= m) f[j + y[a]] -= 1;
}
}
else {
int b = i + x[a], e = i + x[a] + y[a] - 1;
for (int j = b; j <= e; j++) {
last[x[a] + y[a]][j % (x[a] + y[a])]++;
}
}
st[a] = i;
}
else {
if (x[a] + y[a] > s) {
for (int j = st[a] + x[a]; j <= m; j += x[a] + y[a]) {
f[j] -= 1;
if (j < i) sum--;
if (j + y[a] <= m) {
f[j + y[a]] += 1;
if (j + y[a] < i) sum++;
}
}
}
else {
for (int j = st[a] + x[a]; j < st[a] + x[a] + y[a]; j++) {
last[x[a] + y[a]][j % (x[a] + y[a])]--;
}
}
}
sum += f[i];
int res = sum;
for (int j = 1; j <= s; j++) res += last[j][i % j];
cout << res << '\n';
}
return 0;
}
CF1829H Don't Blame Me
题意:
给定一个长度为 \(n\) 的数组,选择它的一个子序列(不一定要连续的),问有多少种选法使得它们 AND 的值的二进制表示法中有 \(k\) 个 \(1\)。
思路:
这个题就是一个简单的 DP,
设 \(f_{i,j}\) 表示选择到了第 \(i\) 个数字(但不一定是把前 \(i\) 个数字都选择了),所有被选择的数字的 AND 值等于 \(j\) 的方案数。
那么我可以不选择这个数字:\(f_{i,j} = f_{i,j} + f_{i-1,j}\),即与选择 \(i - 1\) 个数字,数字的 AND 的值为 \(j\) 的方案数一样。
那么我们也可以选择这个数字:\(f_{i,j\& a_i} = f_{i,j\& a_i} + f_{i - 1,j}\),即从前 \(i - 1\) 个数得到的 \(j\) 与上一个 \(a_i\) 就有前 \(i\) 个数字得到的 \(j\&a_i\)。
当然,我们为什么一定要让第 \(i\) 个数字受到前面的数字的影响呢?我们可以另起炉灶!即 \(f_{i, a_i}=1\)。
这就讨论完了所有情况。
归纳总结起来就是
\[\begin{cases} f_{i,j} = f_{i,j} + f_{i-1,j} \\ f_{i,j\& a_i} = f_{i,j\& a_i} + f_{i - 1,j} \\ f_{i, a_i}=1 \\ \end{cases} \]代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 200010, mod = 1e9 + 7;
int f[N][64];
int n, k;
int a[N];
void solve() {
cin >> n >> k;
for (int i = 1; i <= n; i++) memset(f[i], 0, sizeof(f[i]));
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++) {
f[i][a[i]] = 1;
for (int j = 0; j < 64; j++) {
f[i][j] = (1ll * f[i][j] + f[i - 1][j]) % mod;
f[i][j & a[i]] = (1ll * f[i][j & a[i]] + f[i - 1][j]) % mod;
}
}
int res = 0;
for (int i = 0; i < 64; i++) {
int cnt = 0;
for (int j = 0; j < 6; j++) {
if (i >> j & 1) cnt++;
}
if (cnt == k) res = (1ll * res + f[n][i]) % mod;
}
cout << res << '\n';
}
int main() {
#ifdef DEBUG
freopen("Test.in", "r", stdin);
cout << "===================START===================" << endl;
#endif
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) solve();
#ifdef DEBUG
cout << "====================END====================" << endl;
#endif
return 0;
}
CF1859B Olya and Game with Arrays
题意
给定 \(n\) 个长度为 \(m\) 的数组,每个数组可以向别的数组转移最多一个数字,任意一个数组都可以接受无穷多的数字,最大化每个数组的最小值之和。
做法
考虑贪心。
我们记第 \(i\) 个数组的第 \(j\) 个数字为 \(a_{i, j}\)。
我们先对每一个数组按照升序进行排序,那我们最不愿意看到的就是 \(a_{i, 1}\),因为整个数组的最小值取决于 \(a_{i, 1}\)。
那我们就把 \(n\) 个数组的最小值全部转移到一个数组里面去,假如这个“受害者”是第 \(r\) 个数组 \(a_r\),让它保存所有的最小值 \(a_{i, 1}\)。
这样就让除 \(a_r\) 以外的数组的第 \(2\) 项 \(a_{i, 2}\) 重见光明。
那我们也要榨干第 \(2\) 项,所以我们选择第 \(2\) 项最小的数组作为 \(a_r\)。
最后计算结果为 \(\min\limits_{i = 1}^{n}a_{i, 1} + \sum\limits_{i = 1}^{sz[i]}[i \ne r]a_{i, 2}\)。
可以证明这是最优解。
代码
注意要开 long long。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 25010;
int n;
vector<int> a[N];
void solve() {
cin >> n;
int minn = 0x3f3f3f3f3f3f3f3f, mins = 0x3f3f3f3f3f3f3f3f, ans = 0;
for (int i = 1; i <= n; i++) {
int sz;
cin >> sz;
a[i].resize(sz);
for (int& x : a[i]) cin >> x;
sort(a[i].begin(), a[i].end());
minn = min(minn, a[i][0]);
mins = min(mins, a[i][1]);
ans += a[i][1];
}
ans += minn;
ans -= mins;
cout << ans << '\n';
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) solve();
return 0;
}
CF1859C Another Permutation Problem
思路
我们实际上发现它计算的就是 \(p_i \cdot i\) 的和再减去一个 \(p_i \cdot i\) 中的最大值。
那我们可以枚举这个最大值 \(p_x \cdot x\),这个值就是最后和中需要删除的数值。
这里我们可以使用贪心。
我们可以从 \(n \sim 1\) 枚举除 \(p_i\) 的每个数字需要配的数字。
当然,越大的数字 \(p_i\),配的数字 \(i\) 也应该越大,这样才能使和最大。
我们还要注意选最大的 \(p_i \cdot i\) 一定不能超过 \(p_x \cdot x\)。
加一些剪枝就过了。
最坏时间复杂度:\(O(n^4)\),最多需要跑 \(4.6 \times 10^9\) 次。
因为时间限制有 \(3\) 秒(不要质疑 CF 的机子),所以放心跑。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 260;
bool vis[N];
void solve() {
int n, ans = 0;
cin >> n;
int res = 0;
for (int a = 1; a <= n; a++) {
for (int b = 1; b <= n; b++) {
int maxx = a * b, ans = 0;
if (maxx < n) continue;
if (a * b * n <= res) continue;
memset(vis, 0, sizeof(int) * (n + 10));
vis[b] = true;
for (int i = n; i >= 1; i--) {
if (i == a) continue;
int maxp = min(n, maxx / i);
while (maxp >= 1 && vis[maxp]) maxp--;
if (maxp == 0) {
ans = -0x3f3f3f3f;
break;
}
vis[maxp] = true;
ans += maxp * i;
}
// cout << a << ' ' << b << ' ' << ans << endl;
res = max(res, ans);
}
}
cout << res << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) solve();
return 0;
}
CF1858B The Walkway
思路
注意:所有变量名与原题面相同。
因为 \(1\) 号点必须吃一块饼干,所以我们可以在 \(1\) 立一个不可删除的商店,记为 \(s_0\)。
注意:如果 \(1\) 号附近本身就有一个商店,那就不用立。
然后我们可以在 \(n + 1\) 的位置立一个不可删除的商店,作为一个结束标志,记为 \(s_{m + 1}\)。
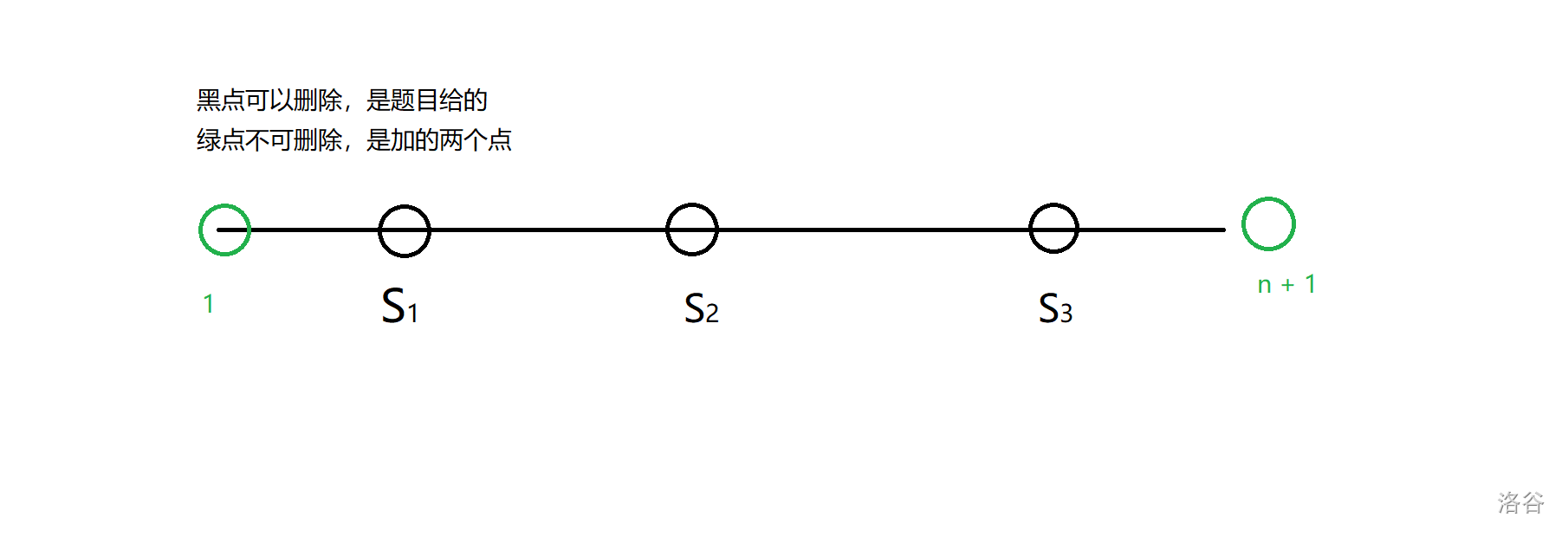
然后我们可以进行分段分为 \(m + 1\) 段,即 \([s_0,s_1),[s_1, s_2),[s_2, s_3),\dots,[s_{m - 1},s_m),[s_m, s_{m + 1})\),注意是左闭右开区间。
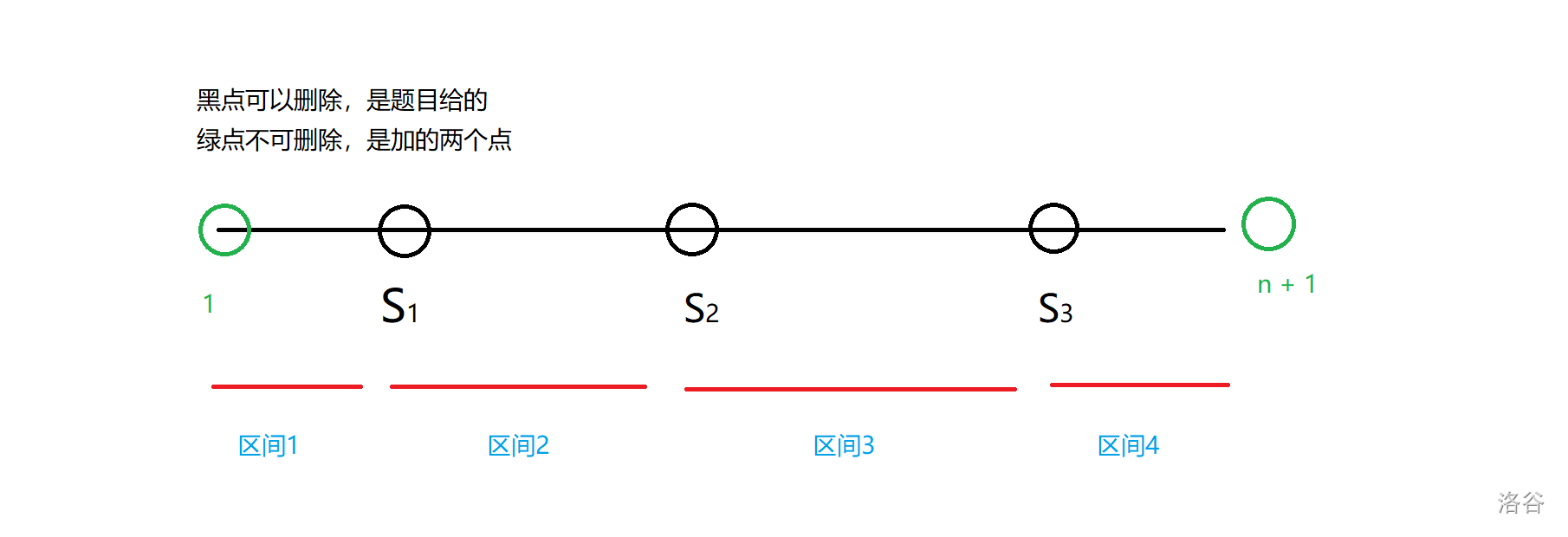
对于区间 \([l, r)\),我们要吃多少饼干呢?画一画就可以知道要吃 \({\left\lceil\frac{r - l}{d}\right\rceil}\) 。
利用这个公式,我们可以求出不删除商店要吃饼干的数量 \(\text{init}\),就是把每一段吃的饼干加起来。
即计算 \(\text{init} = \sum\limits_{i = [s_1 = 1]}^{m}\left\lceil\frac{s_{i + 1} - s_i}{d}\right\rceil\)。
实际上,如果要删掉 \(x\) 商店,
那么只要拿最初的 \(\text{init}\) 删除 \([s_{x - 1}, s_x)\) 和 \([s_x, s_{x + 1})\) 吃的饼干,这是在清除原有数据。
再加上 \([s_{x - 1}, s_{x + 1})\) ,这是在计算删除商店后这一段会吃掉的饼干。
即 \(ans = \text{init} - \left\lceil\frac{s_x - s_{x - 1}}{d}\right\rceil - \left\lceil\frac{s_{x + 1} - s_x}{d}\right\rceil + \left\lceil\frac{s_{x + 1} - s_{x - 1}}{d}\right\rceil\),就是删掉 \(x\) 商店要吃的饼干了。
最后我们求出所有 \(ans\) 的最小值并统计一下数量 \(cnt\) 就可以了。
同时,我们要注意,如果 \(1\) 号点附近本身就有一个商店,那么删掉该商店以后,答案还是 \(\text{init}\),也要参与统计。
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 200010;
int n, m, d;
int s[N];
inline int cnt(int l, int r) {
int sz = r - l;
if (sz % d == 0) return sz / d;
return sz / d + 1;
}
void solve() {
cin >> n >> m >> d;
for (int i = 1; i <= m; i++) cin >> s[i];
bool flag = true;
if (s[1] != 1) {
flag = false;
m++;
for (int i = m; i >= 2; i--) s[i] = s[i - 1];
s[1] = 1;
}
m++;
s[m] = n + 1;
int init = 0;
for (int i = 2; i <= m; i++) init += cnt(s[i - 1], s[i]);
int minn = 0x3f3f3f3f3f3f3f3f, ans = 0;
for (int i = 2; i < m; i++) {
int g = init - cnt(s[i - 1], s[i]) - cnt(s[i], s[i + 1]) + cnt(s[i - 1], s[i + 1]);
if (g < minn) {
minn = g;
ans = 1;
}
else if (g == minn) ans++;
}
if (init < minn && flag) minn = init, ans = 1;
else if (init == minn && flag) minn = init, ans++;
cout << minn << ' ' << ans << '\n';
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) solve();
return 0;
}
CF1858C Yet Another Permutation Problem
思路
这个题是一个简单的构造题。竟然比 T2 简单,也是少见
我们可以首先从 \(1\) 开始不断乘以 \(2\),像这样:\(1, 2, 4, 8, 16\cdots,2^x\),直到什么时候超过 \(n\) 就停止。
这样相邻两个数字的 \(\gcd\) 就可以凑出 \(1, 2, 4, 8, \cdots,2^{x- 1}\)。
\(2\) 已经出现在刚刚的序列中,我们可以选择忽略。
然后我们可以从 \(3\) 开始不断乘以 \(2\),像这样:\(3, 6, 12, 24, \dots, 3 \times 2^x\),直到什么时候超过 \(n\) 就停止。
这样相邻的连个数字就可以凑出 \(3, 9, 18, \cdots, 3\times 2^{x - 1}\)。
剩下的,您应该也明白了,从 \(5\) 开始继续造,然后是 \(7\),因为 \(9\) 已经在 \(3\) 的序列里了,所以 \(7\) 后面的是 \(11\),直到 \(x > n\) 就停止。
最后把剩下的按任意顺序输出就可以了。
可以证明这是最优解。
1 分钟出思路系列
代码
#include <bits/stdc++.h>
using namespace std;
void solve() {
int n;
cin >> n;
vector<bool> a(n + 1, 0);
for (int i = 1; i <= n; i++) {
if (a[i]) continue;
int j = i;
while (j <= n) {
cout << j << ' ';
a[j] = 1;
j <<= 1;
}
}
for (int i = 1; i <= n; i++) {
if (a[i]) continue;
cout << i << ' ';
}
cout << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) solve();
return 0;
}
P9236 [蓝桥杯 2023 省 A] 异或和之和
思路
题目给我们一个数组 \(a\),那么我们可以算出其异或前缀和 \(sum\)。
我们知道,算出 \([l, r]\) 的异或和可以这样计算:\(sum_r \oplus sum_{l - 1}\)。
那么问题就转换为了 \(sum_{0\sim n}\) 这 \(n + 1\) 个数字两两异或之和(当然 \(sum_i \oplus sum_j\) 和 \(sum_j\oplus sum_i\) 是一样的,不重复计算)。
那我们遍历 \(sum\) 数组,然后计算出 \(w_{i, j}\) 数组表示所有数字在二进制表示下第 \(i\) 位为 \(j\) 的数字个数(\(0 \le i \le 20, 0 \le j \le 1\))。
对于第 \(i\) 位,如果有两个数字的第 \(i\) 位分别为 \(0, 1\),那么就可以贡献 \(2^i\) 的和。
根据乘法原理,对于第 \(i\) 位可以凑出 \(w_{i, 0}\cdot w_{i, 1}\) 这么多对可以对答案有贡献的组合,它们的贡献都是 \(2 ^ i\),所以可以让 \(ans\) 加上 \(w_{i, 0}\cdot w_{i, 1}\cdot2^i\)。
代码
注意要开 long long。
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const int N = 100010, M = 25;
int n;
int a[N];
int w[M][2];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i], a[i] ^= a[i - 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j < M; j++) {
w[j][a[i] >> j & 1] ++;
}
}
i64 ans = 0;
for (int i = 0; i < M; i++) ans += (1ll * w[i][0] * w[i][1] * (1 << i));
cout << ans << '\n';
return 0;
}
参考文献:
https://www.luogu.com.cn/blog/w9095/solution-p9236
P1329 数列
思路
题解区的题解都多多少少有些错误。
我想写一写我的做法,是将题解区各大佬的做法综合起来的做法。
首先,假如每一个数字都比前面的一个数字大 \(1\),即数列为 \(0, 1, 2, 3, 4, 5, \dots, n - 1\),那么这个数列的和为 \(sum = \frac{n(n - 1)}{2}\),我们发现 \(n \le 100\),那么 \(sum \le 4950\),所以如果题目要求的 \(s > sum\),那么一定无解,因为这个数列再大也大不过 \(sum\),更不可能到达 \(s\) 了。
反过来,如果一个数字比前面一个数字小 \(1\),即数列为 \(0, -1, -2, -3, -4, -5, \dots, -(n - 1)\),那么这个数列的和为 \(sum = -\frac{n(n - 1)}{2}\),我们发现 \(n \le 100\),那么 \(sum \ge -4950\)。
所以 \(-2^{63} \le s \le 2^{63}\) 是吓你的,真正有用的 \(-4950 \le s \le 4950\)。
接下来,我们来探究一个位子 \(u\) 上的数字变化对数组的和 \(sum\) 的影响。
如果 \(a_u = a_{u - 1} + 1\),现在改成 \(a_{u} = a_{u - 1} - 1\),那么从 \(u\) 开始的每一个数字都会减去 \(2\)。

那么数组的和 \(sum\) 就会减去 \(2(n - u + 1)\)。
那么,我们可以想到让每一个数字都等于前面一个数字 \(+1\),那么和就是 \(\frac{n(n - 1)}{2}\)。
但是我们想让其变为题目要求的 \(s\),那么要减去的数字就是 \(k = \frac{n(n - 1)}{2} - s\)。
那么我们只能将有些数字间的 \(+1\),换成 \(-1\) 才能达到减去 \(k\) 的目的。
那么根据前面对数字间关系的讨论,我们知道,我们要凑出很多个 \(i\),使这些 \(i\) 对应的 \(2(n - i + 1)\) 加起来等于 \(k\) 就行了,即让所有的 \(n - i + 1\) 加起来等于 \(\frac{k}{2}\) 即可。
当然了,如果 \(k\) 是奇数,那么一定无解。
我们考虑 DP,设 \(f_{i, j}\) 表示已经凑到第 \(i\) 个数字,和为 \(j\) 的方案数。
开始时:\(f_{1, 0} = 1\),
目标:\(f_{n, \frac{k}{2}}\)。
我们可以不选择第 \(i\) 个数字,\(f_{i, j} = f_{i - 1, j}\)。
我们可以选择第 \(i\) 个数字,即在原有基础上加上 \((n - i + 1)\),\(f_{i, j} = f_{i - 1, j - (n - i + 1)}\)。
然后爆搜 + 剪枝输出方案就可以了,因为最多输出 \(100\) 项,所以不用担心会不会超时,当然不剪枝是过不了的。
(相信大家都会)
代码
注意取模!!!
因为要模的是 \(2^{64}\) 所以使用 unsigned long long 可以自动溢出。(感谢 @Remilia1023 大佬给的建议)
// Problem: P1329 数列
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1329
// Memory Limit: 128 MB
// Time Limit: 1000 ms
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
using ull = unsigned long long;
const int N = 1010, M = 5010;
ull f[N][M];
int n, k;
i64 s;
int cnt;
int m[N];
void dfs(int u, int sum) {
if (sum > (k >> 1)) return;
if (u > n) {
if (sum == (k >> 1)) {
cnt++;
i64 tmp = 0;
for (int i = 1; i <= n; i++) {
tmp += m[i];
cout << tmp << ' ';
}
cout << '\n';
}
if (cnt >= 100) {
exit(0);
}
return;
}
m[u] = -1;
dfs(u + 1, sum + (n - u + 1));
m[u] = 1;
dfs(u + 1, sum);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> s;
if (s > n * (n - 1) / 2) {
cout << 0 << '\n';
return 0;
}
k = n * (n - 1) / 2 - s;
if (k & 1) {
cout << 0 << '\n';
return 0;
}
f[1][0] = 1;
for (i64 i = 2; i <= n; i++) {
i64 x = (n - i + 1);
memcpy(f[i], f[i - 1], sizeof(f[i]));
for (int j = x; j < M; j++) {
f[i][j] = f[i][j] + f[i - 1][j - x];
}
}
cout << f[n][k >> 1] << '\n';
dfs(2, 0);
return 0;
}
[ABC317G] Rearranging
借鉴了官方题解思路。
思路
首先我们要建立一个二分图。
对于输入的 \(a_{i, j}\),我们可以连接 左侧的 \(i\) 和 右侧的 \(a_{i, j}\)。
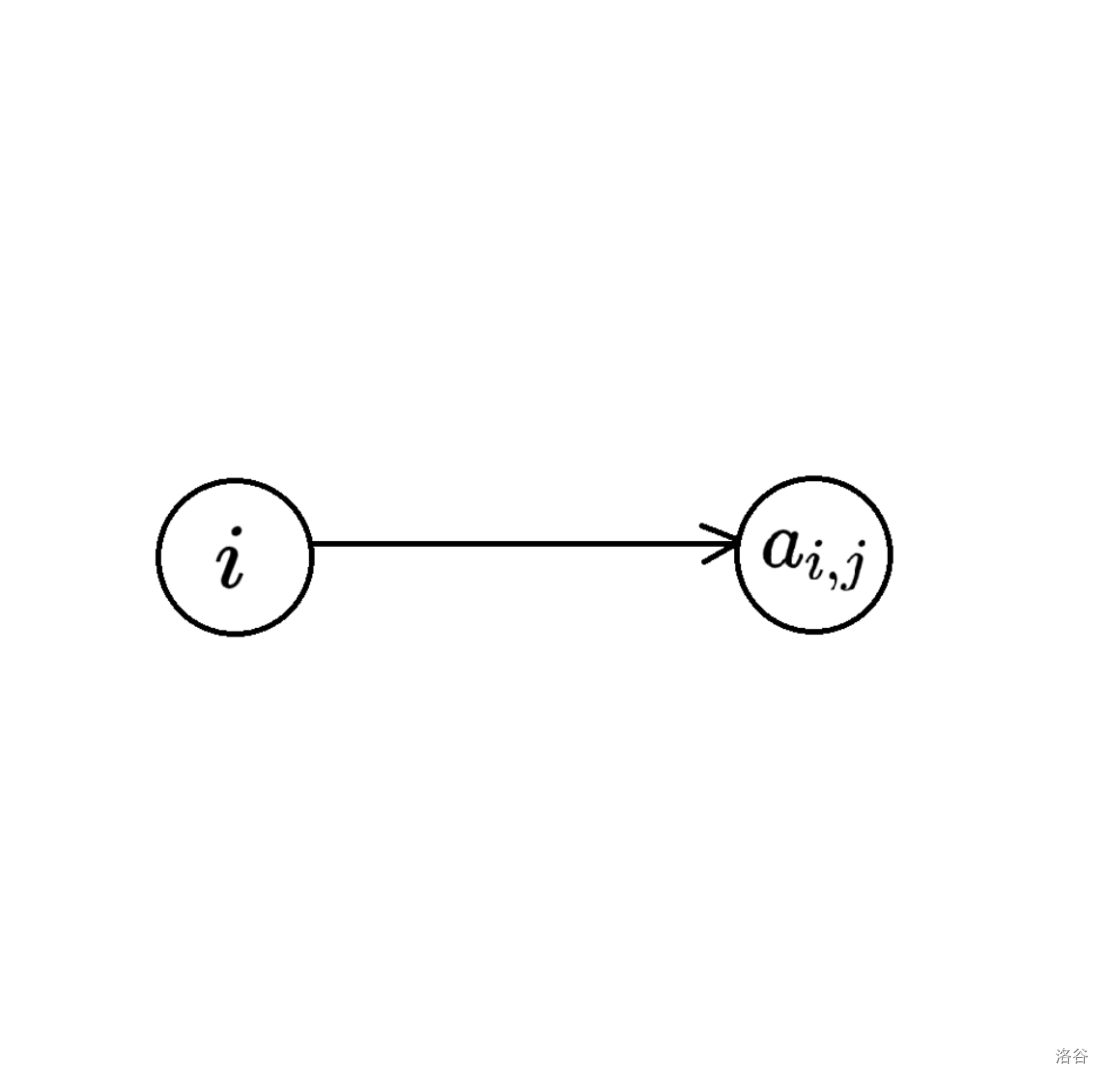
比如样例 \(1\):
注意:左边的 \(1, 2, 3\) 和 右边的 \(1, 2, 3\) 完全不一样,一个是行数,一个是数字。
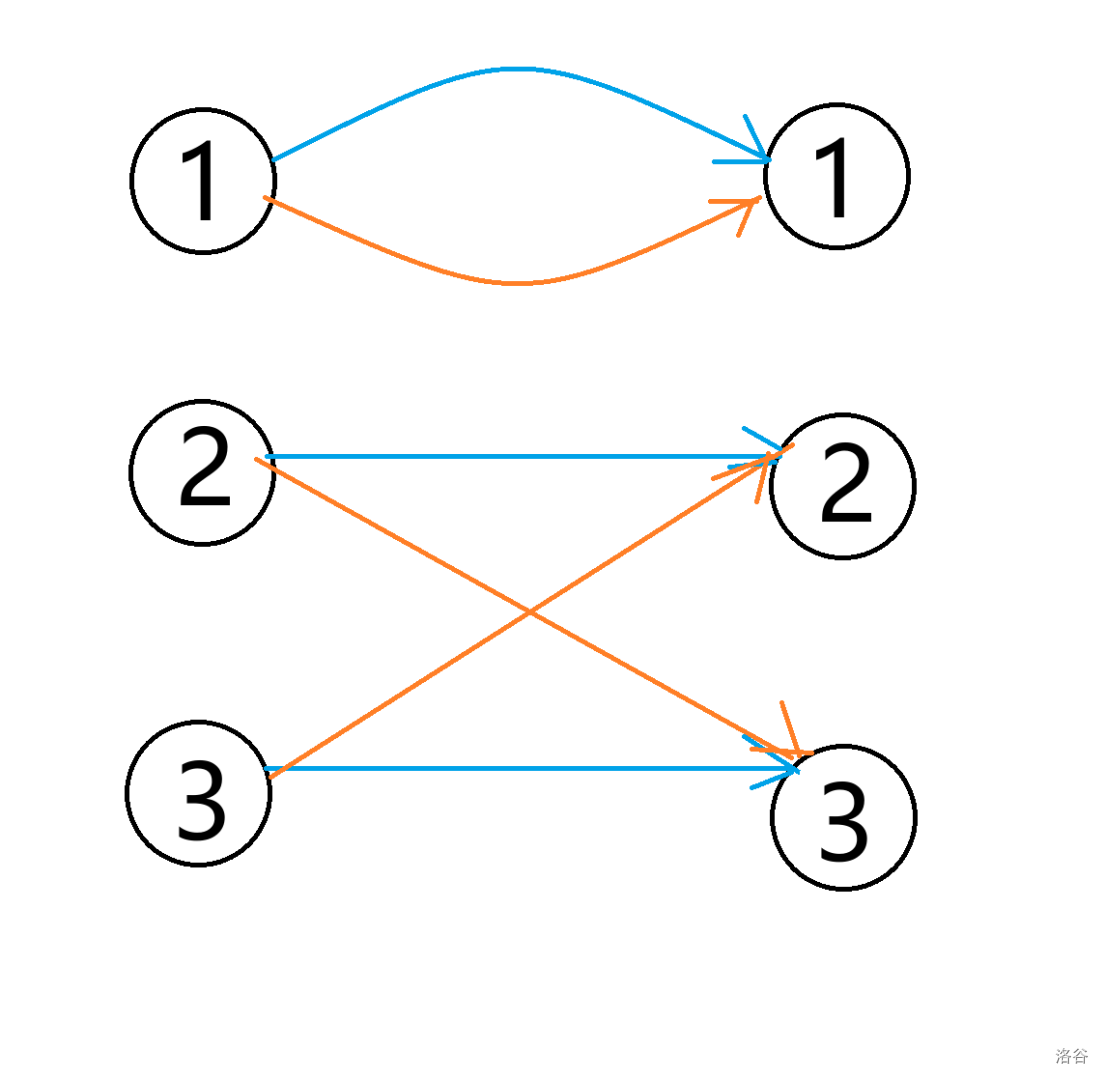
-
那我们现在找出一组二分图的最大匹配,那么就代表对于固定的一列,第 \(i\) 行的数字就可以确定了。
比如上图中橙色的边,它们就是一组二分图的最大匹配,我们可以通过其知道对于一列,可以这么填:
-
我们将已经匹配的边删去,然后再跑下一次的二分图,构建下一列的数字。就这样执行 \(m\) 遍,就可以做出答案。

可以得到最大匹配,然后构建出这一列数字:
- 最后将这么多列数字按任意顺序输出就可以了。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 210, M = 40010, INF = 0x3f3f3f3f;
struct edge {
int to, next, w;
} e[M];
int head[N], idx = 1;
void add(int u, int v, int w) {
idx++, e[idx].to = v, e[idx].next = head[u], e[idx].w = w, head[u] = idx;
idx++, e[idx].to = u, e[idx].next = head[v], e[idx].w = 0, head[v] = idx;
}
int S, T;
int n, m;
int q[N], hh, tt;
int d[N];
int ans[N][N];
bool bfs() {
memset(d, 0, sizeof(d));
hh = tt = 0;
q[0] = S;
d[S] = 1;
while (hh <= tt) {
int u = q[hh++];
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if ((!d[to]) && e[i].w) {
d[to] = d[u] + 1;
q[++tt] = to;
}
}
}
return d[T];
}
int dinic(int u, int limit) {
if (u == T) return limit;
int rest = limit;
for (int i = head[u]; i && rest; i = e[i].next) {
int to = e[i].to;
if (d[to] == d[u] + 1 && e[i].w) {
int k = dinic(to, min(rest, e[i].w));
if (!k) d[to] = INF;
rest -= k;
e[i].w -= k;
e[i ^ 1].w += k;
}
}
return limit - rest;
}
int maxflow() {
int ans = 0, flow = 0;
while (bfs()) while (flow = dinic(S, INF)) ans += flow;
return ans;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
S = 0, T = n << 1 | 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
int x;
cin >> x;
add(i, x + n, 1);
}
}
int tmp = idx;
for (int i = 1; i <= n; i++) add(S, i, 1), add(i + n, T, 1);
for (int j = 1; j <= m; j++) {
if (maxflow() != n) {
cout << "No\n";
return 0;
}
for (int i = 3; i <= tmp; i += 2) if (e[i].w == 1) {
int u = e[i].to, v = e[i ^ 1].to;
ans[u][j] = v - n;
e[i].w = e[i ^ 1].w = 0;
}
for (int i = tmp + 2; i <= idx; i += 2) {
if (e[i].w == 1) {
e[i ^ 1].w = 1;
e[i].w = 0;
}
}
}
cout << "Yes\n";
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cout << ans[i][j] << ' ';
}
cout << '\n';
}
return 0;
}
CF1863D. Two-Colored Dominoes
前言
一个普及组 T3 难度的题耗费了我近 40 分钟。
总的来说我太弱了。
思路
我们首先来想一想怎么满足让每一行的黑白数量相同。
我们发现,横着摆的多米诺骨牌对每一行的黑白数量没有影响,反正黑白数量都 \(+1\)。
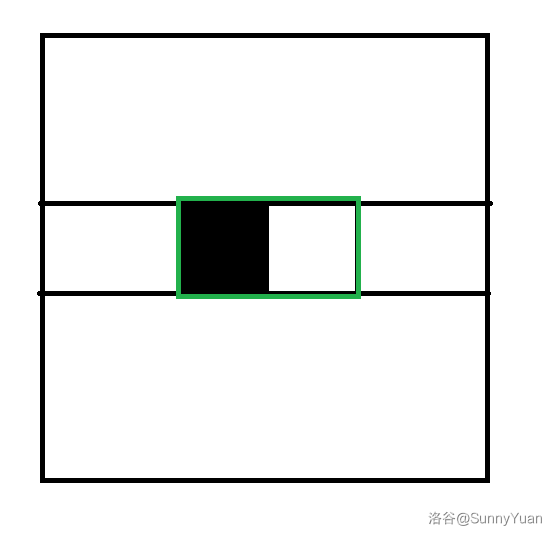
那么只有竖着摆(竖着摆指上面的方框在这一行)对这一行的黑白数量有影响,假设这一行竖着摆的有 \(cnt\) 个,如果 \(cnt\) 是奇数,那么肯定无解;否则,我们将 \(\frac{cnt}{2}\) 个染成上面黑下面白,将另外 \(\frac{cnt}{2}\) 个染成上面白下面黑。
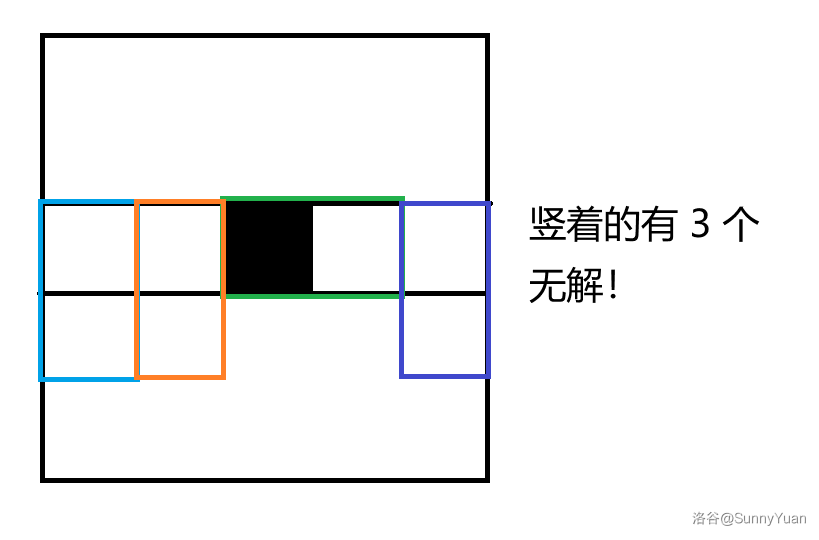
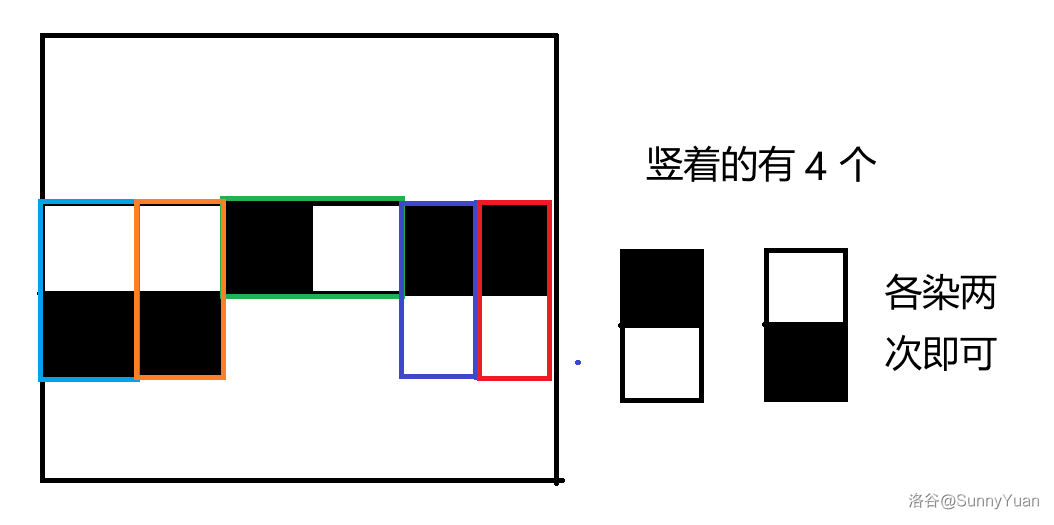
我们考虑了横着摆和竖着摆对每一行的黑白数量的影响。
那我们可以用相同的方法考虑横着摆和竖着摆对每一列的黑白数量的影响。
我们发现只有当横着摆(横着摆指左边的方框在这一行)的时候会对每一列的数量产生影响。
所以我们可以用刚刚同样的方法得出:假设这一列有 \(cnt\) 个横着摆的,如果 \(cnt\) 为奇数,那么无解,否则将 \(\frac{cnt}{2}\) 染成左边黑右边白,另外 \(\frac{cnt}{2}\) 染成左边白右边黑。
代码
/*******************************
| Author: SunnyYuan
| Problem: D. Two-Colored Dominoes
| Contest: Pinely Round 2 (Div. 1 + Div. 2)
| URL: https://codeforces.com/contest/1863/problem/D
| When: 2023-08-30 22:35:21
|
| Memory: 256 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
const int N = 510;
int n, m;
char g[N][N];
void solve() {
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> (g[i] + 1);
for (int i = 1; i <= n; i++) {
vector<int> s;
for (int j = 1; j <= m; j++) {
if (i < n && g[i][j] == 'U' && g[i + 1][j] == 'D') s.push_back(j);
}
int sz = s.size();
if (sz & 1) {
cout << -1 << '\n';
return;
}
for (int k = 0; k < (sz >> 1); k++) g[i][s[k]] = 'W', g[i + 1][s[k]] = 'B';
for (int k = (sz >> 1); k < sz; k++) g[i][s[k]] = 'B', g[i + 1][s[k]] = 'W';
}
for (int j = 1; j <= m; j++) {
vector<int> s;
for (int i = 1; i <= n; i++) {
if (j < m && g[i][j] == 'L' && g[i][j + 1] == 'R') s.push_back(i);
}
int sz = s.size();
if (sz & 1) {
cout << -1 << '\n';
return;
}
for (int k = 0; k < (sz >> 1); k++) g[s[k]][j] = 'W', g[s[k]][j + 1] = 'B';
for (int k = (sz >> 1); k < sz; k++) g[s[k]][j] = 'B', g[s[k]][j + 1] = 'W';
}
for (int i = 1; i <= n; i++) cout << (g[i] + 1) << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) solve();
return 0;
}
P4055 [JSOI2009] 游戏
思路
我主要讲一讲怎么找到可以让先手赢的点。
先说一说基本思路:
可以想到将该图黑白染色,让其成为二分图。
然后再在每个白点上连接其可以到达的点。
- 存在完美匹配,先手必败。
因为不论先手将棋子放在哪里,后手都可以走这个点的所在的最大匹配边,总能在先手移动完以后做出移动,所以先手必败。
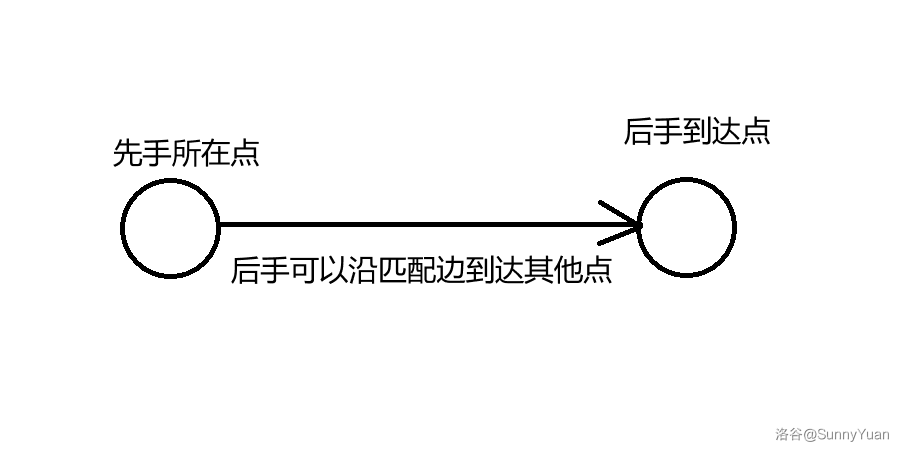
- 不存在完美匹配,先手必胜。
先手可以将棋子放在非匹配点,后手必走非匹配边来到匹配点,那么先手就可以一直走匹配边,所以先手必胜。
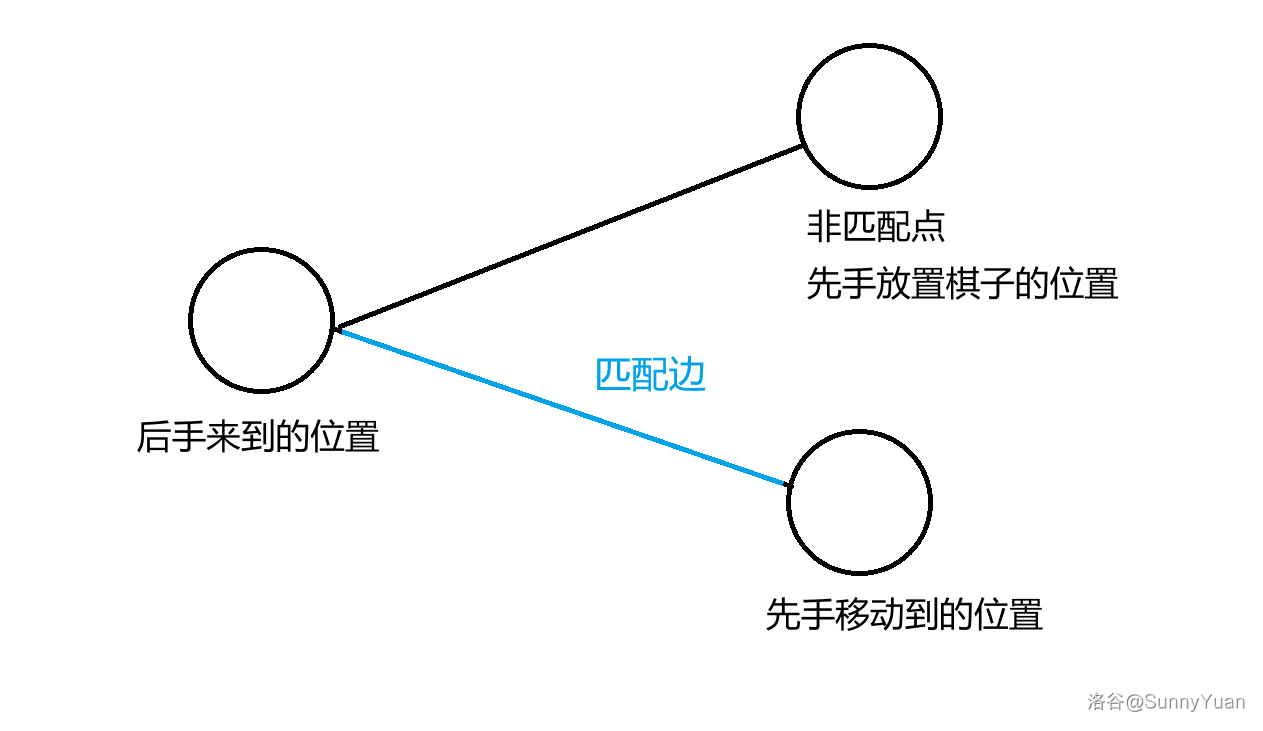
实际上非匹配点可以看作非必须点,删掉它也不会影响最大匹配数量。
所以实际上我们现在就要想一想怎样才能找到非必须点。
如果我们发现一个点 \(u\) 沿着一条边到达一个匹配点 \(v\),且该点的匹配点不是 \(u\),那么我们就可以将原来的一条匹配边换成 \(u-v\)。
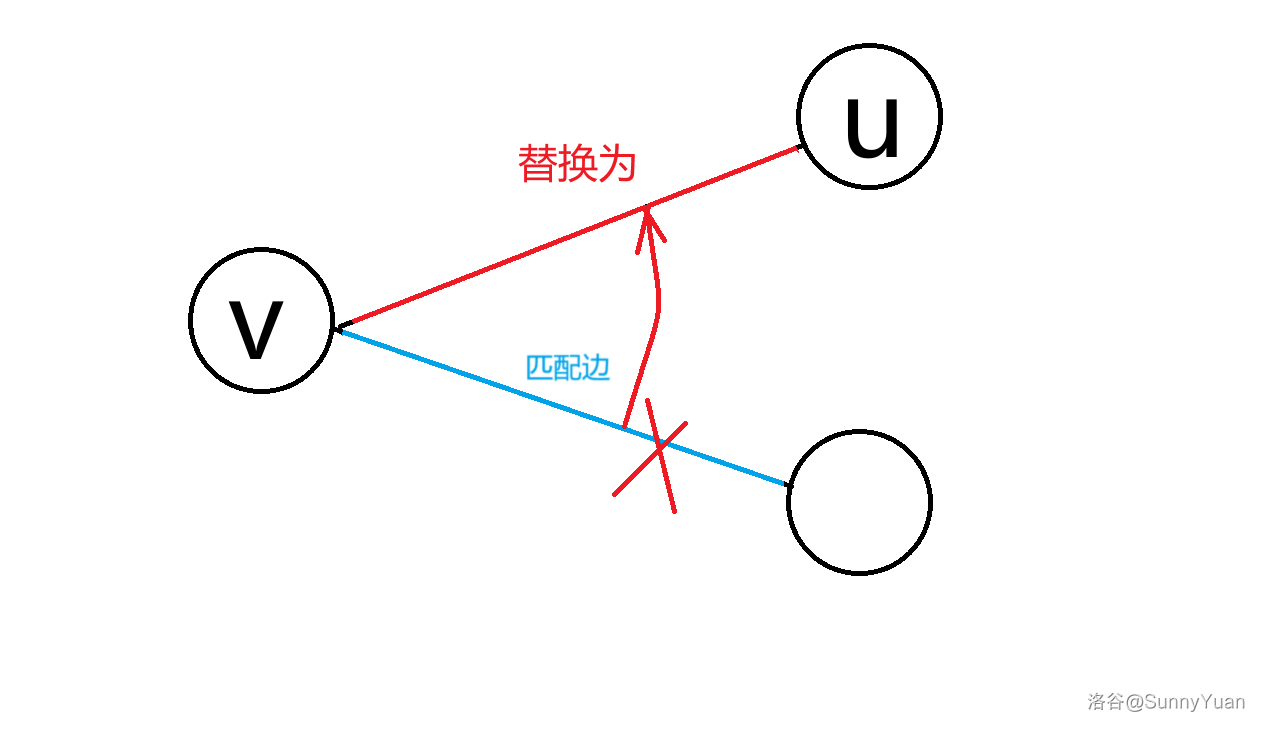
于是,我们只要从一个点 \(u\) 开始 dfs 如果还能回到同侧的一个匹配点,那么那个匹配点就是非必须点。
我们通过这种方法就可以找到所有可以让先手赢的点。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 110, K = N * N;
const int dx[4] = {1, 0, -1, 0};
const int dy[4] = {0, 1, 0, -1};
vector<int> e[K];
int n, m;
char g[N][N];
int a[N][N];
bool vis[K];
int match[K];
int dfs(int u) {
for (int to : e[u]) {
if (!vis[to]) {
vis[to] = true;
if ((!match[to]) || dfs(match[to])) {
match[to] = u;
match[u] = to;
return 1;
}
}
}
return 0;
}
int win[K];
void getwin(int u) {
vis[u] = true;
for (int to : e[u]) {
if ((!match[to]) || (match[to] == u) || vis[match[to]]) continue;
win[match[to]] = true;
getwin(match[to]);
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> (g[i] + 1);
for (int i = 1; i <= n; i++) iota(a[i] + 1, a[i] + m + 1, (i - 1) * m + 1);
int c = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (((i + j) & 1) && (g[i][j] != '#')) {
for (int k = 0; k < 4; k++) {
int nx = i + dx[k], ny = j + dy[k];
if (nx < 1 || ny < 1 || nx > n || ny > m || g[nx][ny] == '#') continue;
e[a[i][j]].push_back(a[nx][ny]);
e[a[nx][ny]].push_back(a[i][j]);
}
}
if (g[i][j] != '#') c++;
}
}
int cnt = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (((i + j) & 1) && (g[i][j] != '#')) {
memset(vis, 0, sizeof(vis));
cnt += dfs(a[i][j]);
}
}
}
if (cnt == (c >> 1) && (!(c & 1))) {
cout << "LOSE\n";
return 0;
}
cout << "WIN\n";
memset(vis, 0, sizeof(vis));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if ((!match[a[i][j]]) && (g[i][j] != '#')) {
win[a[i][j]] = 1;
getwin(a[i][j]);
}
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (win[a[i][j]]) {
cout << i << ' ' << j << '\n';
}
}
}
return 0;
}
UVA10004 Bicoloring
随机跳到的。
思路
这个是一个二分图的判定的模板题。
主要思路就是判断图中是否有奇环。
我们主要是对图进行染色。
相邻的两个点采取不同的颜色。
像这样:
如果染色染到中途发现点 \(u\) 和 点 \(v\) 之间右边相连且颜色相同,说明出现矛盾(就可以返回并输出 NOT BICOLORABLE.)。
如果到最后都没有遇到错误,那么输出 BICOLORABLE.。
代码
/*******************************
| Author: SunnyYuan
| Problem: In 1976 the \Four Color Map Theorem " was proven with the assistance of a computer. This theorem - states that every map can be colored using only four colors, in such a way that no region is colored
| Contest: UVa Online Judge
| URL: https://onlinejudge.org/external/100/p10004.pdf
| When: 2023-09-06 15:41:13
|
| Memory: 1024 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
const int N = 210;
int n, m;
vector<int> e[N];
int color[N];
bool dfs(int u, int col) {
color[u] = col;
for (int to : e[u]) {
if (!color[to]) {
if (!dfs(to, 3 - col)) return false;
}
else {
if (color[to] == color[u]) return false;
}
}
return true;
}
void solve() {
for (int i = 0; i < n; i++) {
color[i] = 0;
e[i].clear();
}
for (int i = 1; i <= m; i++) {
int u, v;
cin >> u >> v;
e[u].push_back(v);
e[v].push_back(u);
}
for (int i = 0; i < n; i++) {
if (!color[i]) {
if (!dfs(i, 1)) {
cout << "NOT BICOLORABLE.\n";
return;
}
}
}
cout << "BICOLORABLE.\n";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
while (cin >> n >> m, n) solve();
return 0;
}
P2065 [TJOI2011] 卡片
思路
我们只要将源点与每一个蓝点相连,将每一个红点与汇点相连。
然后将每个蓝点的数值进行质因数分解,然后将这个蓝点与质因数分解出来的每一个质数相连;
然后将每个红点的数值进行质因数分解,然后将质因数分解出来的质数与对应红点进行相连。
最后跑一边网络最大流就可以了。
字丑勿喷
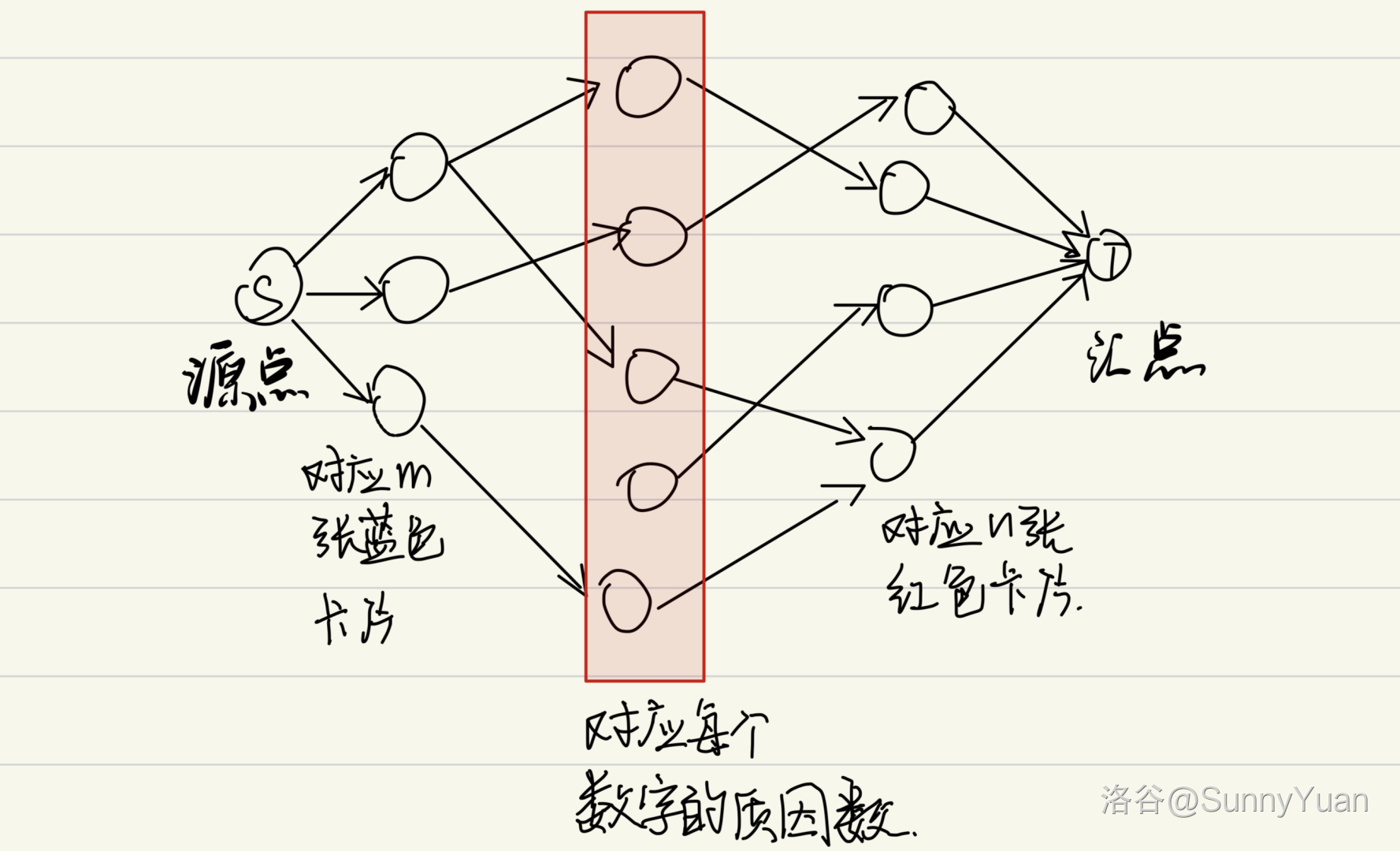
代码
/*******************************
| Author: SunnyYuan
| Problem: P2065 [TJOI2011] 卡片
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P2065
| When: 2023-09-05 20:26:40
|
| Memory: 125 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
const int N = 10010, M = 1000010, INF = 0x3f3f3f3f, K = 10000010;
bool inp[K];
int prime[K], cnt;
void getprime() {
inp[0] = inp[1] = 1;
for (int i = 2; i < K; i++) {
if (!inp[i]) prime[++cnt] = i;
for (int j = 1; j <= cnt && prime[j] * i < K; j++) {
inp[prime[j] * i] = true;
if (i % prime[j] == 0) break;
}
}
}
struct edge {
int to, next, w;
} e[M];
int head[N], idx = 1;
void add(int u, int v, int w) {
idx++, e[idx].to = v, e[idx].next = head[u], e[idx].w = w, head[u] = idx;
idx++, e[idx].to = u, e[idx].next = head[v], e[idx].w = 0, head[v] = idx;
}
int d[N], q[N], hh, tt;
int S, T;
bool bfs() {
hh = tt = 0;
q[0] = S;
memset(d, 0, sizeof(d));
d[S] = 1;
while (hh <= tt) {
int t = q[hh++];
for (int i = head[t]; i; i = e[i].next) {
int to = e[i].to;
if ((!d[to]) && e[i].w) {
d[to] = d[t] + 1;
q[++tt] = to;
}
}
}
return d[T];
}
int dinic(int u, int limit) {
if (u == T) return limit;
int rest = limit;
for (int i = head[u]; i && rest; i = e[i].next) {
int to = e[i].to;
if ((d[to] == d[u] + 1) && e[i].w) {
int k = dinic(to, min(rest, e[i].w));
if (!k) d[to] = INF;
rest -= k;
e[i].w -= k;
e[i ^ 1].w += k;
}
}
return limit - rest;
}
int n, m;
int a[N], b[N];
unordered_map<int, int> s;
int tot;
void solve() {
memset(head, 0, sizeof(head));
idx = 1;
cin >> n >> m;
S = 0, T = N - 1;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int j = 1; j <= m; j++) cin >> b[j];
for (int i = 1; i <= n; i++) add(S, i, 1);
for (int j = 1; j <= m; j++) add(j + n, T, 1);
s.clear();
tot = n + m;
for (int k = 1; k <= n; k++) {
int x = a[k];
for (int i = 1; prime[i] * prime[i] <= x; i++) {
if (x % prime[i] == 0) {
int sx = s[prime[i]];
if (!sx) sx = s[prime[i]] = ++tot;
add(k, sx, 1);
while (x % prime[i] == 0) x /= prime[i];
}
}
if (x > 1) {
if (!s[x]) s[x] = ++tot;
add(k, s[x], 1);
}
}
for (int k = 1; k <= m; k++) {
int x = b[k];
for (int i = 1; prime[i] * prime[i] <= x; i++) {
if (x % prime[i] == 0) {
int sx = s[prime[i]];
if (sx) add(sx, k + n, 1);
while (x % prime[i] == 0) x /= prime[i];
}
}
if (x > 1 && s[x]) add(s[x], k + n, 1);
}
int maxflow = 0, flow = 0;
while (bfs()) while (flow = dinic(S, INF)) maxflow += flow;
cout << maxflow << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
getprime();
int T;
cin >> T;
while (T--) solve();
return 0;
}
P5903 【模板】树上 k 级祖先
思路
长链剖分模板题。
长链剖分:
- 计算 \(f[i][j]\) 表示 \(i\) 的 \(2^j\) 级祖先;
- 计算 \(up[i][j]\) 表示 \(i\) 的 \(j\) 级祖先;
- 计算 \(down[i][j]\) 表示在长链上从 \(i\) 向下走 \(j\) 步到达的祖先。
- 计算 \(i\) 的 \(k\) 级祖先,先让 \(i\) 跳到 \(2^{\lfloor \log_2k\rfloor}\) 级祖先,\(k\) 减去 \(2^{\lfloor \log_2k \rfloor}\),再让 \(i\) 跳到长链顶端,\(k\) 减去 \(dep[i] - dep[top[i]]\),最后如果 \(k \ge 0\),那么答案就是 \(up[i][k]\),否则 \(k < 0\),答案就是 \(down[i][-k]\)。
代码
// Problem: P5903
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5903
// Memory Limit: 500 MB
// Time Limit: 3000 ms
#include <bits/stdc++.h>
using namespace std;
using uint = unsigned int;
#define int long long
const int N = 500010, M = 20;
struct edge {
int to, next;
} e[N];
int head[N], idx;
void add(int u, int v) {
idx++;
e[idx].to = v;
e[idx].next = head[u];
head[u] = idx;
}
int n, q, s;
uint get_rand(uint x) {
x ^= x << 13;
x ^= x >> 17;
x ^= x << 5;
return s = x;
}
int rt;
int fa[N][M];
void initfa() {
for (int j = 1; j < M; j++) {
for (int i = 1; i <= n; i++) {
fa[i][j] = fa[fa[i][j - 1]][j - 1];
}
}
}
int dep[N], ds[N], son[N];
void dfs(int u) {
dep[u] = ds[u] = dep[fa[u][0]] + 1;
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
dfs(to);
if (ds[to] > ds[u]) {
ds[u] = ds[to];
son[u] = to;
}
}
}
vector<int> up[N];
vector<int> down[N];
int belong[N];
void init(int u, int p) {
belong[u] = p;
if (u == p) {
int tmp = u;
for (int i = 0; i <= ds[u] - dep[u]; i++) {
up[u].push_back(tmp);
tmp = fa[tmp][0];
}
tmp = u;
for (int i = 0; i <= ds[u] - dep[u]; i++) {
down[u].push_back(tmp);
tmp = son[tmp];
}
}
if (son[u]) init(son[u], p);
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (to == son[u]) continue;
init(to, to);
}
}
int query(int u, int k) {
if (!k) return u;
u = fa[u][__lg(k)];
k -= 1 << (__lg(k));
k -= dep[u] - dep[belong[u]];
u = belong[u];
if (k >= 0) return up[u][k];
else return down[u][-k];
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> q >> s;
for (int i = 1; i <= n; i++) {
cin >> fa[i][0];
if (!fa[i][0]) rt = i;
if (fa[i][0]) add(fa[i][0], i);
}
initfa();
dfs(rt);
init(rt, rt);
int ans = 0, res = 0;
int x, k;
for (int i = 1; i <= q; i++) {
x = ((get_rand(s) ^ ans) % n) + 1;
k = ((get_rand(s) ^ ans) % dep[x]);
ans = query(x, k);
res ^= (i * ans);
}
cout << res << '\n';
return 0;
}
POJ 3071 Football
思路
这个题目可以使用概率 DP。
设 \(f_{i, j}\) 表示在第 \(i\) 轮第 \(j\) 个人获胜的概率是多少,答案就是在在 \(f_{n, 1\sim m}\) 中寻找最大值。
第 \(i\) 轮第 \(j\) 个人和第 \(k\) 个人对战时,第 \(j\) 个人可以赢的概率是 \(f_{i, j} = f_{i - 1, j} \times f_{i - 1, k} \times a_{j, k}\)。
然后只要根据位运算的规律就可以让我找出可以跟第 \(i\) 个人对战的人有哪些。
代码
/*******************************
| Author: SunnyYuan
| Problem: Football
| Contest: POJ - Stanford Local 2006
| URL: http://poj.org/problem?id=3071
| When: 2023-09-08 10:35:39
|
| Memory: 65 MB
| Time: 1000 ms
*******************************/
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 130;
int n;
double a[N][N], f[N][N];
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
while (cin >> n) {
if (n == -1) break;
int all = 1 << n;
for (int i = 0; i < all; i++)
for (int j = 0; j < all; j++)
cin >> a[i][j];
memset(f, 0, sizeof(f));
for (int i = 0; i < all; i++) f[0][i] = 1;
for (int k = 1; k <= n; k++) { // Round k
for (int i = 0; i < all; i++) { // person i
for (int j = 0; j < all; j++) { // calc p{win(i, j)}
if (((i >> (k - 1)) ^ 1) == (j >> (k - 1))) {
f[k][i] += f[k - 1][i] * f[k - 1][j] * a[i][j];
}
}
}
}
int pos = -1;
double maxx = -1.0;
for (int i = 0; i < all; i++) {
if (f[n][i] > maxx) {
maxx = f[n][i];
pos = i;
}
}
cout << pos + 1 << '\n';
}
return 0;
}
CF1658D2 388535 (Hard Version)
题意
原题面讲的很清楚了,我再来复述一下。
有一个长度为 \(r - l + 1\) 的排列 \(p\),满足 \(l \le p_i\le r\),让我们找一个 \(x\) 满足,对于每一个 \(a_i = p_i \oplus x\),现在给你 \(a\) 数组,让你找到一个可能的 \(x\)。
思路
异或有如下性质:\(a \oplus b = c\),那么 \(a \oplus c = b\)。
因为 \(a_i = p_i \oplus x\),所以 \(a_i \oplus x = p_i\)。
因为 \(l \le p_i\le r\),所以 \(l \le a_i \oplus x \le r\)。
自然而然地,我们可以想到,我们可以枚举 \(x\),在序列 \(a\) 中找到可以异或出来的最大值 \(\max\) 和最小值 \(\min\),如果 \(\max = r\) 且 \(\min = l\),那么现在枚举的 \(x\) 就是答案!
那么在一个序列中找到一个数字 \(x\) 可以异或出来的最大值和最小值,不就是妥妥的字典树吗?
不会的参见 Hydro H1002。
我们将 \(a\) 数组放入字典树,然后找出 \(x\) 可以异或出来的最大值和最小值,判断它是否分别等于 \(r\) 和 \(l\),相等则输出 \(x\),否则继续枚举 \(x\)。
那我们不能瞎枚举 \(x\) 啊,数字有千千万万个,我们还要进行优化。
因为一定存在 \(a_i \oplus x = l\),那么一定有 \(a_i \oplus l = x\)。
即答案 \(x\),一定存在这 \(n\) 个数字中:\(\{a_i \oplus l\}\)。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 3000010, M = 19;
int tr[N][2], idx;
void add(int x) { // 将 x 放入字典树
int p = 0;
for (int i = M - 1; i >= 0; i--) {
int g = (x >> i & 1);
if (!tr[p][g]) tr[p][g] = ++idx;
p = tr[p][g];
}
}
int getnum(int x, int type) { // type 为 1 表示取最小值,type 为 2 表示取最大值
int res = 0, p = 0;
for (int i = M - 1; i >= 0; i--) {
int g = x >> i & 1;
if (type == 1) { // min
if (tr[p][g]) p = tr[p][g];
else p = tr[p][g ^ 1], res ^= (1 << i);
}
else { // max
if (tr[p][g ^ 1]) p = tr[p][g ^ 1], res ^= (1 << i);
else p = tr[p][g];
}
}
return res;
}
int l, r, n;
void solve() {
memset(tr, 0, sizeof(tr[0]) * (idx + 10)); // 初始化
idx = 0;
cin >> l >> r;
n = r - l + 1;
vector<int> b;
for (int i = 0; i < n; i++) { // 输入 a[i](懒得用数组存了)
int x;
cin >> x;
b.push_back(x ^ l); // 记录每一个可能的 x。
add(x); // 将 x 放入字典树
}
for (int i = 0; i < n; i++) {
if (getnum(b[i], 1) == l && getnum(b[i], 2) == r) {// 判断
cout << b[i] << '\n'; // 答案
return;
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) solve();
return 0;
}
P8816 [CSP-J 2022] 上升点列
前言
水一水去年的 CSP-J。
思路
我们先对所有点进行排序,\(x\) 为第一关键字,\(y\) 为第二关键字。
设 \(f_{i, j}\) 表示考虑到第 \(i\) 个点,增加了 \(j\) 个点可以获得的序列的最大长度。
初始条件:\(f_{i, j} = j + 1\),表示本身有一个点,我们人为地加上 \(j\) 个点,可以构成长度为 \(j + 1\) 的序列。
对于从第 \(j\) 个点转移到第 \(i\) 个点需要增加 \(add_{i,j} = i_x - j_x + i_y - j_y - 1\) 个点,前提是满足 \(x_i > x_j, y_i > y_j\)。
状态转移:\(f_{i, k} = \max\limits_{j = 1}^{i - 1}\{f_{j, k - add_{i, j}} + add_{i, j} + 1\}\),注意第 \(j\) 个点还需满足 \(x_i > x_j, y_i > y_j\)。
代码
/*******************************
| Author: SunnyYuan
| Problem: P8816 [CSP-J 2022] 上升点列
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P8816
| When: 2023-09-08 20:02:18
|
| Memory: 512 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
using PII = pair<int, int>;
const int N = 510, M = 110;
int f[N][M];
PII p[N];
int n, m;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> p[i].first >> p[i].second;
sort(p + 1, p + n + 1);
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++)
f[i][j] = j + 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j < i; j++) {
if (p[j].second > p[i].second) continue;
int add = p[i].second - p[j].second + p[i].first - p[j].first - 1;
for (int k = add; k <= m; k++) f[i][k] = max(f[i][k], f[j][k - add] + add + 1);
}
}
int ans = m;
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++)
ans = max(ans, f[i][j] + m - j);
cout << ans << '\n';
return 0;
}
P8817 [CSP-S 2022] 假期计划
思路
我们可以使用 bfs 求出图上任意两点之间的最短路径。
对于每一个点 \(u\),处理出 \(v\) 表示 \(v\) 在 \(1\sim u\) 这段路径中(不包括 点 \(1\) 和点 \(u\))且到 \(1\) 和 \(u\) 的距离都小于题目规定的 \(k\),并将它们按照分数从大到小进行排序,只保留最大的,次大的,和第三大的,将其放入集合 \(S_u\) 中。
然后对于 \(A, B, C, D\) 四点,我们考虑只枚举 \(B, C\) 两点,首先要满足 \(B, C\) 两点间的距离 \(dis_{B, C} \le k\)。\(B\) 给我们带来了 \(S_B\) 这个集合,\(C\) 给我们带来了 \(S_C\) 这个集合,我们从 \(S_B\) 中选取一个点作为 \(A\),但是不能与 \(C, D\) 重合,也要从 \(S_C\) 中选取一个点作为 \(D\) ,但是不能与 \(A, B\) 相等(这也是为什么要储存 \(3\) 个点的原因:防止冲突)。
代码
/*******************************
| Author: SunnyYuan
| Problem: P8817 [CSP-S 2022] 假期计划
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P8817
| When: 2023-09-08 16:30:05
|
| Memory: 512 MB
| Time: 2000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
using PII = pair<i64, int>;
const int N = 2510, M = 20010;
const i64 INF = 4e18;
struct edge {
int to, next;
} e[M];
int head[N], idx = 1;
void add(int u, int v) {
idx++, e[idx].to = v, e[idx].next = head[u], head[u] = idx;
}
int n, m, s;
int q[N], hh, tt;
i64 a[N], dis[N][N];
void bfs(int u) {
hh = tt = 0;
q[0] = u;
for (int i = 1; i <= n; i++) dis[u][i] = INF;
dis[u][u] = 1;
while (hh <= tt) {
int t = q[hh++];
for (int i = head[t]; i; i = e[i].next) {
int to = e[i].to;
if (dis[u][to] == INF) {
dis[u][to] = dis[u][t] + 1;
q[++tt] = to;
}
}
}
}
set<PII> g[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m >> s;
s += 2;
for (int i = 2; i <= n; i++) cin >> a[i];
for (int i = 1; i <= m; i++) {
int u, v;
cin >> u >> v;
add(u, v), add(v, u);
}
for (int i = 1; i <= n; i++) bfs(i);
for (int i = 2; i <= n; i++)
for (int j = 2; j <= n; j++)
if (i != j && dis[i][j] <= s && dis[1][j] <= s)
g[i].insert({-a[j], j});
int t1[3], t2[3];
i64 ans = -4e18;
for (int b = 2; b <= n; b++) {
for (int c = b + 1; c <= n; c++) {
if (dis[b][c] > s) continue;
int c1 = 0, c2 = 0;
for (auto x : g[b]) {
t1[c1++] = x.second;
if (c1 == 3) break;
}
for (auto x : g[c]) {
t2[c2++] = x.second;
if (c2 == 3) break;
}
for (int i = 0; i < c1; i++) {
for (int j = 0; j < c2; j++) {
int x = t1[i], y = t2[j]; // a, d
if (x != b && x != c && x != y && y != b && y != c) {
ans = max(ans, 1ll * a[x] + a[b] + a[c] + a[y]);
}
}
}
}
}
cout << ans << '\n';
return 0;
}
P8818 [CSP-S 2022] 策略游戏
思路
这个题目很板,静态区间求最值。
我们可以建立 \(6\) 个 ST 表,分别存储:
- 数组 \(a\) 的区间最大值。
- 数组 \(a\) 的区间最小值。
- 数组 \(a\) 的区间非负最小值。
- 数组 \(a\) 的区间负数最大值。
- 数组 \(b\) 的区间最大值。
- 数组 \(b\) 的区间最小值。
然后,如果选择的 \(a\) 的数字 \(x\) 是正数,那么在 \(b\) 中肯定选择最小值与 \(x\) 相乘;如果选择的 \(a\) 是负数,那么在 \(b\) 中肯定选择最大值与 \(x\) 相乘。
代码
/*******************************
| Author: SunnyYuan
| Problem: P8818 [CSP-S 2022] 策略游戏
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P8818
| When: 2023-09-08 17:58:20
|
| Memory: 512 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const int N = 100010, L = 20, INF = 1e9;
int maxx[N][L], minn[N][L];
int maxf[N][L], minz[N][L];
int maxb[N][L], minb[N][L];
int n, m, q;
inline void init() {
for (int j = 1; j < L; j++) {
for (int i = 1; i + (1 << j) - 1 <= n; i++) {
maxx[i][j] = max(maxx[i][j - 1], maxx[i + (1 << (j - 1))][j - 1]);
minn[i][j] = min(minn[i][j - 1], minn[i + (1 << (j - 1))][j - 1]);
maxf[i][j] = max(maxf[i][j - 1], maxf[i + (1 << (j - 1))][j - 1]);
minz[i][j] = min(minz[i][j - 1], minz[i + (1 << (j - 1))][j - 1]);
}
}
for (int j = 1; j < L; j++) {
for (int i = 1; i + (1 << j) - 1 <= m; i++) {
maxb[i][j] = max(maxb[i][j - 1], maxb[i + (1 << (j - 1))][j - 1]);
minb[i][j] = min(minb[i][j - 1], minb[i + (1 << (j - 1))][j - 1]);
}
}
}
inline int query(int a[][20], int l, int r, int type) {
int len = r - l + 1;
int lg = __lg(len);
if (type == 1) return min(a[l][lg], a[r - (1 << lg) + 1][lg]);
else return max(a[l][lg], a[r - (1 << lg) + 1][lg]);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m >> q;
for (int i = 1; i <= n; i++) {
int x;
cin >> x;
maxx[i][0] = minn[i][0] = x;
if (x >= 0) minz[i][0] = x, maxf[i][0] = -INF;
else minz[i][0] = INF, maxf[i][0] = x;
}
for (int i = 1; i <= m; i++) {
int x;
cin >> x;
maxb[i][0] = minb[i][0] = x;
}
init();
int l1, r1, l2, r2;
while (q--) {
cin >> l1 >> r1 >> l2 >> r2;
i64 ans = -1e18;
int x1 = query(maxx, l1, r1, 2);
int x2 = query(minn, l1, r1, 1);
int x3 = query(maxf, l1, r1, 2);
int x4 = query(minz, l1, r1, 1);
int b1 = query(minb, l2, r2, 1);
int b2 = query(maxb, l2, r2, 2);
ans = max(ans, 1ll * x1 * (x1 >= 0 ? b1 : b2));
ans = max(ans, 1ll * x2 * (x2 >= 0 ? b1 : b2));
if (x3 > -INF) ans = max(ans, 1ll * x3 * (x3 >= 0 ? b1 : b2));
if (x4 < INF) ans = max(ans, 1ll * x4 * (x4 >= 0 ? b1 : b2));
cout << ans << '\n';
}
return 0;
}
P1971 [NOI2011] 兔兔与蛋蛋游戏
题解
我主要画几张图帮助大家理解。
思路
为了避免过于空虚,我先简述一下思路:
棋子太多,我们无法考虑这么多棋子的移动方式。
所以,我们可以想到用空格移动来代替棋子的移动,在移动过程中,空格的颜色也会变成棋子的颜色。比如一个白棋子移动到了空格里面,就可以理解为空格移动到了白棋子原有位置并变成了白空格,一个黑棋子移动到了空格里面就可以理解为空格移动到了黑棋子原有位置并变成了黑空格。
所以在空格的移动中,空格的颜色是黑-白-黑-白-黑-白这样交替的。
然后我们发现如果空格到过 \((x, y)\),就再也不会进入 \((x, y)\),且路径不会相交。
接着我们可以想到,将相邻的不同的颜色的点用边相连,形成二分图。
重点来了:
如果二分图的最大匹配覆盖了空格且空格是必须点,那么先手必胜。
因为先手总能根据最大匹配走到右边。
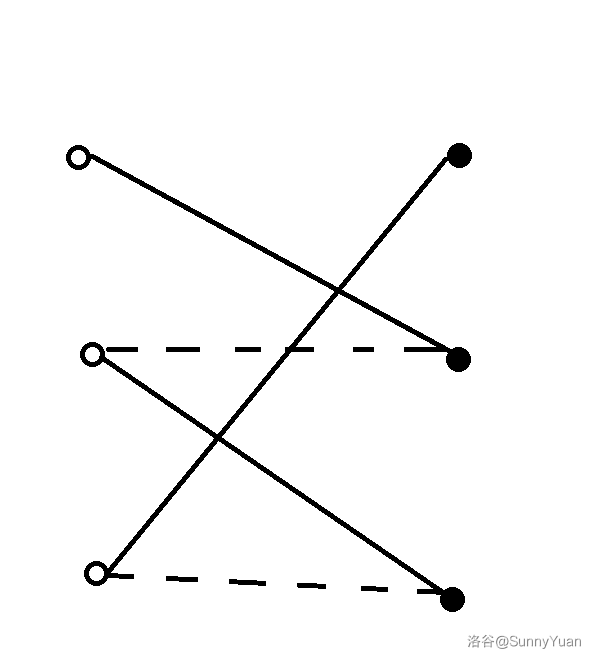
比如这张图,实线表示匹配边,虚线表示非匹配边。
空格不论在哪里,先手先操作,都可以沿着匹配边(实线)到达另一边,但是后手就不一定能沿着非匹配边回来了:
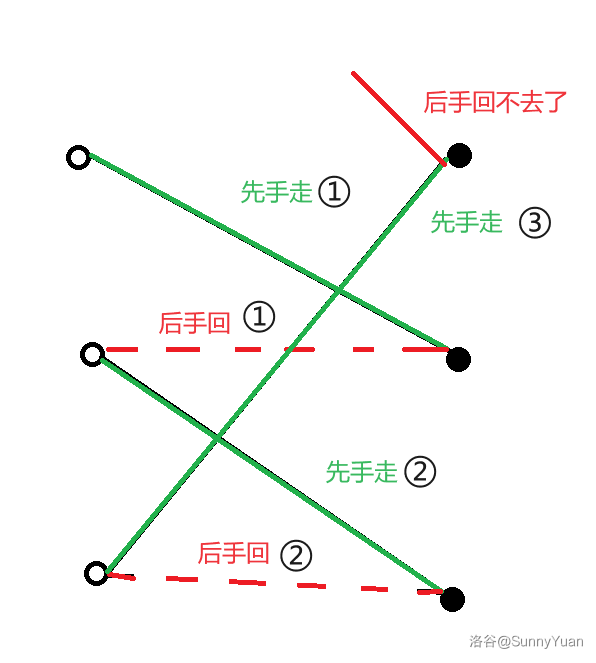
如果空格不是最大匹配的必须点,即失去这个点最大匹配不变。先手先操作,一定会沿着非匹配边到达匹配点,然后,后手就可以一直沿着匹配边到达另一边,先手就不一定能回来了。
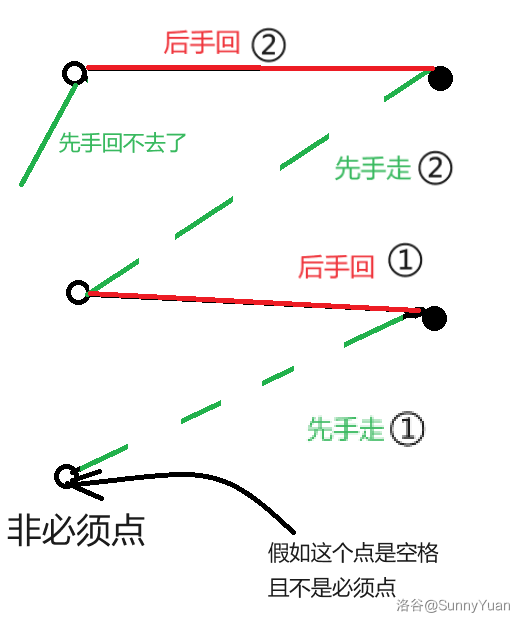
这个题目要求让你判断每个操作是否正确。
那我们就可以暴力跑二分图,如果去掉空格后的二分图的最大匹配不变,那么兔兔必败,说明它做错了。然后还要检查它的这个匹配是否是唯一的,假如空格所在点为 \(u\),那么它的匹配点 \(match[u]\) 如果还可以找到其他匹配边来替代当前匹配,也说明空格点是非必须点,兔兔必败,它做错了。
代码
代码主要的分为
- 二分图的最大匹配:匈牙利算法(
dfs函数)。 - 将一个点 \(u\) 删除并重新计算最大匹配(
cut函数)。 - 将点 \(u\) 进行匹配(
link函数)。 - 强制将 \(u, v\) 两点进行匹配(
connect函数)。 - 对每一步进行处理(
solve函数)。
/*******************************
| Author: SunnyYuan
| Problem: P1971 [NOI2011] 兔兔与蛋蛋游戏
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P1971
| When: 2023-09-04 23:30:45
|
| Memory: 125 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
const int N = 50, K = N * N;
const int dx[4] = {1, 0, -1, 0}, dy[4] = {0, 1, 0, -1};
vector<int> e[K];
int n, m, q;
char g[N][N];
int a[N][N];
int space_x, space_y;
int match[K];
bool vis[K], state[K];
vector<int> ans;
int match_cnt;
bool dfs(int u) {
for (int to : e[u]) {
if (vis[to]) continue;
vis[to] = true;
if ((!state[to]) && ((!match[to])||dfs(match[to]))) {
match[to] = u;
match[u] = to;
return true;
}
}
return false;
}
void cut(int u) {
if (!match[u]) return;
int mt = match[u];
match[u] = match[mt] = 0;
match_cnt--;
state[u] = true;
memset(vis, 0, sizeof(vis));
match_cnt += dfs(mt);
}
void link(int u) {
// if (match[u]) return;
state[u] = 0;
memset(vis, 0, sizeof(vis));
match_cnt += dfs(u);
}
void connect(int u, int v) {
if (match[u] == v) {
state[u] = state[v] = 1;
return;
}
// clear
int m1 = match[u], m2 = match[v];
if (m1) match[u] = match[m1] = 0, match_cnt--;
if (m2) match[v] = match[m2] = 0, match_cnt--;
match[u] = v, match[v] = u;
state[u] = state[v] = 1;
match_cnt++;
if (m1) {
memset(vis, 0, sizeof(vis));
match_cnt += dfs(m1);
}
if (m2 && (!match[m2])) {
memset(vis, 0, sizeof(vis));
match_cnt += dfs(m2);
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1; i <= n; i++) iota(a[i] + 1, a[i] + m + 1, (i - 1) * m + 1);
for (int i = 1; i <= n; i++) cin >> (g[i] + 1);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (g[i][j] == '.') space_x = i, space_y = j, g[i][j] = 'X';
if (g[i][j] == 'X') {
for (int k = 0; k < 4; k++) {
int nx = i + dx[k], ny = j + dy[k];
if (nx < 1 || ny < 1 || nx > n || ny > m || g[nx][ny] != 'O') continue;
e[a[i][j]].push_back(a[nx][ny]);
e[a[nx][ny]].push_back(a[i][j]);
}
}
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (g[i][j] == 'X') {
memset(vis, 0, sizeof(vis));
match_cnt += dfs(a[i][j]);
}
}
}
cin >> q;
for (int p = 1; p <= q; p++) {
int nx, ny;
cin >> nx >> ny;
int cur = a[space_x][space_y];
int nxt = a[nx][ny];
cut(cur);
int tmp = match_cnt;
link(cur);
int tmp2 = match_cnt;
connect(cur, nxt);
if (tmp != tmp2) {
bool f = true;
int ys = match_cnt;
for (int to : e[nxt]) {
if (state[to]) continue;
cut(to);
tmp = match_cnt;
link(to);
if (tmp == ys) {
f = false;
break;
}
}
if (!f) ans.push_back(p);
}
cin >> space_x >> space_y;
}
cout << ans.size() << '\n';
for (auto x : ans) cout << x << '\n';
return 0;
}
参考文献
CF1869C / CF1868A Fill in the Matrix
前言
感谢 @Ziqqurat 发现错别字。
思路
情况 1
如果 \(m \le n\),那么一定能构造出答案为 \(m\) 的数组。
我们让每一列凑出来的 \(\text{MEX}\) 合在一起为 \(0 \sim m - 1\) 即可,这样整个数组可以凑出来的 \(\text{MEX}\) 就为 \(m\) 了。
我们可以让 \(0 \sim m\) 组成一个长度为 \(m + 1\) 的数组,然后不断循环:
比如 \(m = 5\):
原始数组:\(0, 1, 2, 3, 4\)
不断循环:
\(0, 1, 2, 3, 4\)
\(1, 2, 3, 4, 0\)
\(2, 3, 4, 0, 1\)
\(3, 4, 0, 1, 2\)
\(4, 0, 1, 2, 3\)
然后我们将这一行行数字塞到每一列中(从第二个数字开始),将第一个数字看成 \(\text{MEX}\)。
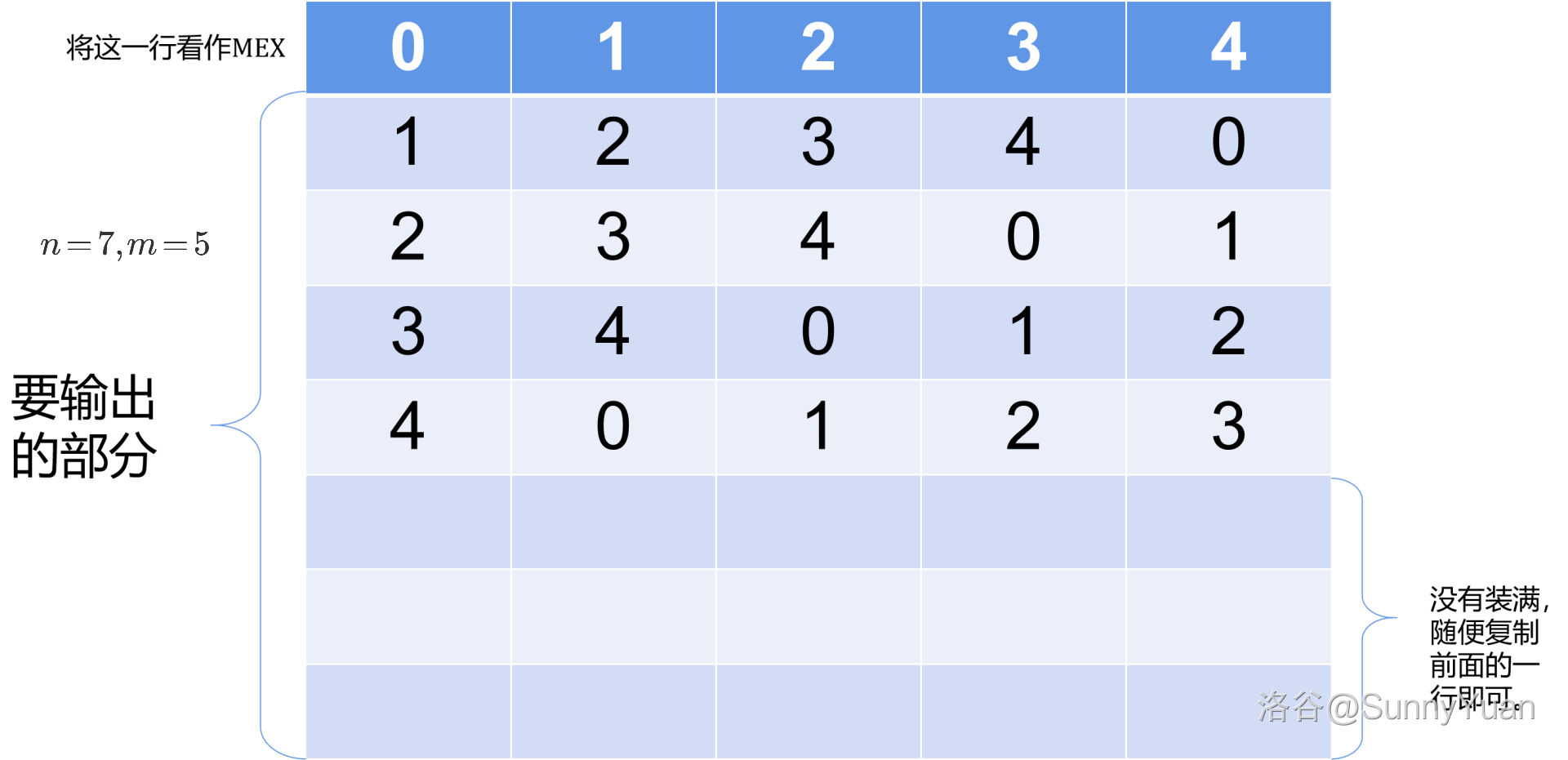
如果 \(n\) 行没有装满,我们就可以随便复制前面的一行。
将最上面一行的 \(\text{MEX}\) 再求 \(\text{MEX}\),就可以得到最终答案 \(m\)。
情况 2
如果 \(m > n\),那么我们就可以凑出 \(\text{MEX}\) 为 \(n + 1\)。
一样的,我们构造一个 \(0 \sim n + 1\) 的长度为 \(n + 2\) 的数组,然后不断循环。
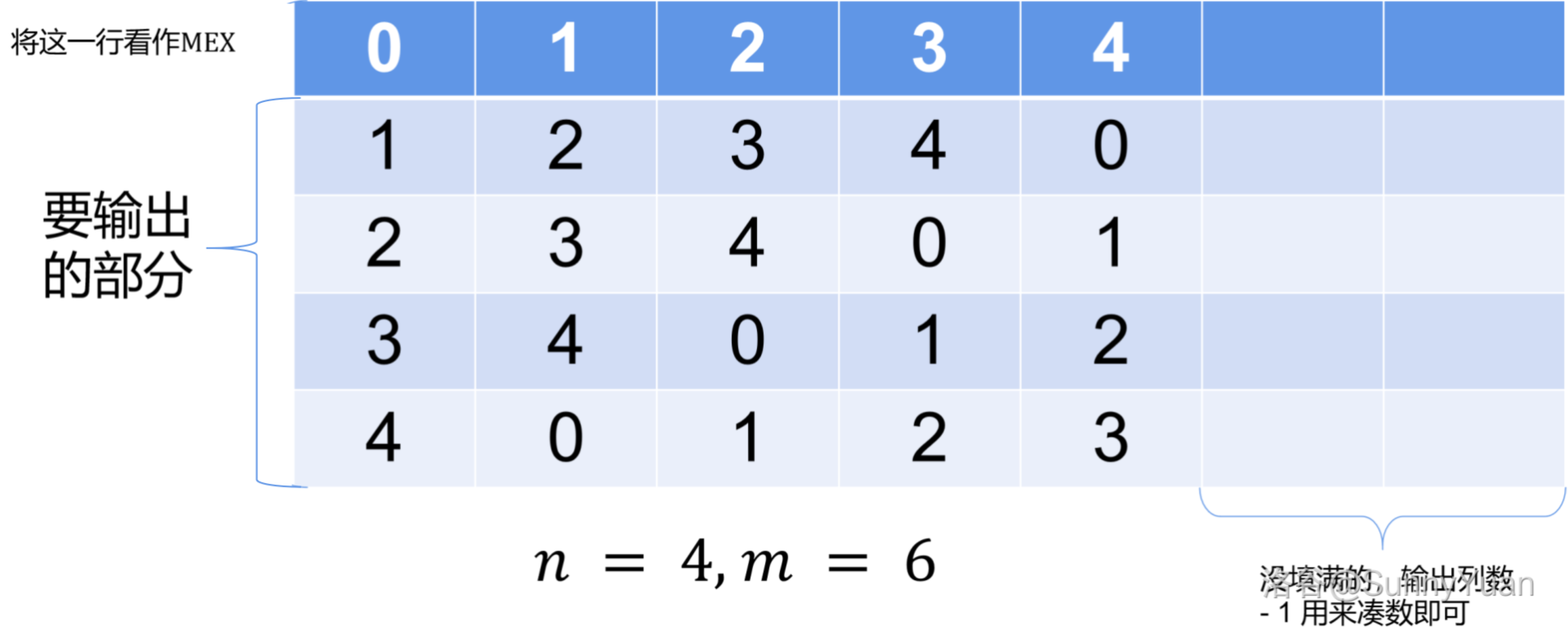
将最上面一行的 \(\text{MEX}\) 再求 \(\text{MEX}\),就可以得到最终答案 \(n + 1\)。
代码
#include <bits/stdc++.h>
using namespace std;
int n, m;
void solve() {
cin >> n >> m;
if (m == 1) {
cout << "0\n";
for (int i = 1; i <= n; i++) cout << "0\n";
return;
}
if (n == 1) {
cout << "2\n";
for (int i = 0; i < m; i++) cout << i << ' ';
cout << '\n';
return;
}
vector<vector<int> > a(n + 1);
for (int i = 0; i <= n; i++) {
for (int j = -1; j < m; j++) {
a[i].push_back(j);
}
}
if (n < m) {
for (int j = 1; j <= n + 1; j++) {
for (int i = 0, st = j; i <= n; i++, st++) {
a[i][j] = st % (n + 1);
}
}
cout << n + 1 << '\n';
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cout << a[i][j] << ' ';
}
cout << '\n';
}
}
else {
for (int j = 1; j <= m; j++) {
for (int i = 0, st = j; i < m; i++, st++) {
a[i][j] = st % m;
}
}
cout << m << '\n';
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cout << a[min(i, m - 1)][j] << ' ';
}
cout << '\n';
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) solve();
return 0;
}
CF1869B. 2D Traveling
思路
如果 \(a, b \le k\),那么从 \(a\) 直接到 \(b\) 不需要花钱。
然后我们来想一想如何应对 \(a, b\) 两个都不 \(\le k\)。
接下来就又分了 \(2\) 种情况:
- 从 \(a\) 直接到 \(b\),花费 \(|x_a - x_b| + |y_a - y_b|\)。
- 从 \(a\) 到离 \(a\) 最近的编号小于等于 \(k\) 的城市 \(v\),然后再免费到离 \(b\) 最近的编号小于等于 \(k\) 的城市 \(u\),再到 \(b\),花费 \(|x_v - x_a| + |y_v - y_a| + |x_u - x_b| + |y_u - y_b|\)。
最后我们再来想一想如何应对 \(a, b\) 有一个 \(\le k\) 的情况:
假设 \(b \le k\) 且 \(a > k\),如果不是这样,交换一下 \(a, b\) 对答案没有影响。
又分为 \(2\) 种情况:
- 从 \(b\) 直接到 \(a\),花费 \(|x_a - x_b| + |y_a - y_b|\)。
- 从 \(b\) 免费到离 \(a\) 最近的编号小于等于 \(k\) 的城市 \(u\),然后再到 \(b\),花费 \(|x_u - x_b| + |y_u - y_b|\)。
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 200010;
int n, k, a, b;
int x[N], y[N];
int dis(int a, int b) {
return llabs(x[a] - x[b]) + llabs(y[a] - y[b]);
}
void solve() {
cin >> n >> k >> a >> b;
for (int i = 1; i <= n; i++) cin >> x[i] >> y[i];
if (a <= k && b <= k) {
cout << "0\n";
return;
}
bool flag = false;
if ((a <= k) && (b > k)) swap(a, b);
if ((b <= k) && (a > k)) flag = true;
int mdis = 0x3f3f3f3f3f3f3f3f, xdis = 0x3f3f3f3f3f3f3f3f;
for (int i = 1; i <= k; i++) mdis = min(mdis, dis(i, a));
for (int i = 1; i <= k; i++) xdis = min(xdis, dis(i, b));
int ans = dis(a, b);
if (flag) ans = min(ans, mdis);
ans = min(ans, xdis + mdis);
cout << ans << '\n';
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) solve();
return 0;
}
P1311 [NOIP2011 提高组] 选择客栈
思路
据说有 \(O(n)\) 做法,但是这题可以用 \(O(n log n)\) 的做法。
首先我们处理一个前缀和 \(sum[c][i]\) 表示 \(1\sim i\) 中有多少个颜色为 \(c\) 的客栈。
然后我们处理一个 ST 表,记录价格,计算 \([l, r]\) 的区间最小值。
因为要住进两个颜色相同的客栈,所以我们可以先枚举左边的客栈,坐标为 \(u\),然后二分出编号最小的点 \(v\) 使得 \([u, v]\) 的最小值 \(k \le p\),这样就保证了 \(u\) 和 \(v\) 后面的(包括 \(u\))的所有客栈都能找到消费小于等于 \(p\) 的地方,同时要求颜色相同,所以只有 \(s[c][n] - s[c][\max(i + 1, v) - 1]\) 个。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 200010, M = 20, K = 55, INF = 0x3f3f3f3f;
int n, k, p;
int f[N][M];
int cost[N];
int color[N];
int s[K][N];
inline int sum(int c, int l, int r) {
return s[c][r] - s[c][l - 1];
}
inline void init() {
for (int j = 1; j < M; j++) {
for (int i = 1; i + (1 << j) - 1 <= n; i++) {
f[i][j] = min(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
}
}
}
inline int query(int l, int r) {
if (l < 1 || r < 1 || l > n || r > n) return INF;
int len = r - l + 1;
int lg = __lg(len);
return min(f[l][lg], f[r - (1 << lg) + 1][lg]);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> k >> p;
for (int i = 1; i <= n; i++) {
cin >> color[i] >> cost[i];
f[i][0] = cost[i];
s[color[i]][i] = 1;
}
for (int i = 0; i < k; i++) {
for (int j = 1; j <= n; j++) {
s[i][j] += s[i][j - 1];
}
}
init();
int ans = 0;
for (int i = 1; i <= n; i++) {
int l = i, r = n + 1;
while (l < r) {
int mid = l + r >> 1;
if (query(i, mid) <= p) r = mid;
else l = mid + 1;
}
if (l == n + 1) break;
ans += sum(color[i], max(l, i + 1), n);
}
cout << ans << '\n';
return 0;
}
P3467 [POI2008] PLA-Postering
思路
很有趣的一个题。
我们可以使用单调栈来维护高度。
当我们处理一个新的高度 \(h\) 比栈顶元素大时就弹出,然后不断重复此操作,直到小于等于 \(h\) 时停止弹出,因为原来比自己高度大的海报不能延申到这里,要开一个新的。
弹出完成以后,如果当前栈顶元素小于 \(h\),那么说明不能使用之前的海报,要加入新的海报了,否则等于 \(h\) 还可以使用原来的海报。
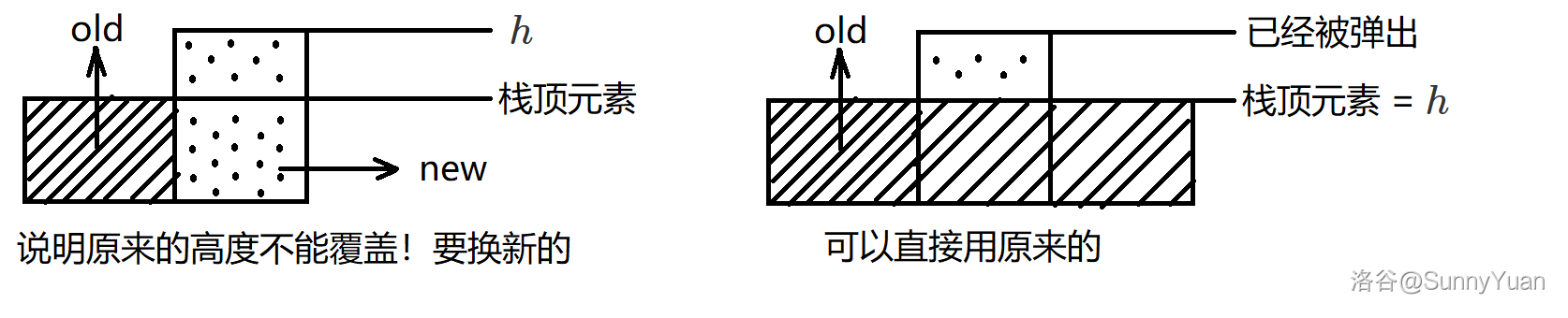
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 250010;
int n;
stack<int> s;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
int ans = 0;
for (int i = 1; i <= n; i++) {
int w, h;
cin >> w >> h;
while (s.size() && (s.top() > h)) s.pop();
if (s.empty() || s.top() != h) ans++;
s.push(h);
}
cout << ans << '\n';
return 0;
}
P6835 [Cnoi2020] 线形生物
思路
我们设 \(E_{x\rightarrow y}\) 为从 \(x\) 到 \(y\) 的期望长度。
那么 \(E_{x\rightarrow y} = E_{x->x + 1} + E_{x + 1\rightarrow x + 2} + E_{x + 2 \rightarrow x + 3} + \dots + E_{y - 1 \rightarrow y}\)。
那么从 \(1\) 号点到 \(n + 1\) 号点就是 \(E_{1\rightarrow n + 1} = \sum\limits_{i = 1}^{n} E_{i\rightarrow i + 1}\)
注意从 \(x\) 到 \(x + 1\) 不一定只走一条边,也有可能走到返祖边再回来。
设 \(out_u\) 表示点 \(u\) 的出度(不包括 \(u\rightarrow u + 1\) 这条边)。
我们发现,我们既可以从 \(u\) 到 \(u + 1\),也可以从 \(u\) 由返祖边回到之前的一个点然后再到 \(u + 1\),设返祖边构成的集合为 \(R\),有:
\[E_{u\rightarrow u + 1} = \frac{1}{out_u + 1}\times 1 + \frac{1}{out_u + 1}\sum\limits_{(u, v) \in R}{(1 + E_{v\rightarrow u + 1})} \]\(\frac{1}{out_u + 1}\times 1\) 表示有 \(\frac{1}{out_u + 1}\) 的概率从 \(u\) 直接走到 \(u + 1\),并且长度为 \(1\),期望为 \(\frac{1}{out_u + 1}\times 1\)。
\(\frac{1}{out_u + 1}\sum\limits_{(u, v) \in R}{(1 + E_{v\rightarrow u + 1})}\) 表示有 \(\frac{1}{out_u + 1}\) 的概率走到每一条返祖边里面,每次走的长度为从 \(u\) 到 \(v\) 的长度 \(1\) 加上 \(v\rightarrow u + 1\) 的期望长度 \(E_{v\rightarrow u + 1}\)。
然后我们发现 \(E_{v\rightarrow u + 1} = \sum\limits_{d = v}^{u} E_{d\rightarrow d + 1}\)。
带入原式得
\[E_{u\rightarrow u + 1} = \frac{1}{out_u + 1}\times 1 + \frac{1}{out_u + 1}\sum\limits_{(u, v) \in R}{(1 + \sum\limits_{d = v}^{u} E_{d\rightarrow d + 1})} \]继续化简,将 \(\sum\limits_{(u, v) \in R}{(1 + \sum\limits_{d = v}^{u} E_{d\rightarrow d + 1})}\) 继续化简得 \(out_u + \sum\limits_{(u, v) \in R}{\sum\limits_{d = v}^{u} E_{d\rightarrow d + 1}}\),放回到原式得
\[\begin{aligned} E_{u\rightarrow u + 1} &= \frac{1}{out_u + 1} + \frac{out_u}{out_u + 1} + \frac{1}{out_u + 1}\sum\limits_{(u, v) \in R}{\sum\limits_{d = v}^{u} E_{d\rightarrow d + 1}}\\ &= 1 + \frac{1}{out_u + 1}\sum\limits_{(u, v) \in R}{\sum\limits_{d = v}^{u} E_{d\rightarrow d + 1}} \end{aligned} \]现在我们设 \(f_i\) 为 \(E_{i\rightarrow i + 1}\),有:
\[f_u = 1 + \frac{1}{out_u + 1}\sum\limits_{(u, v) \in R}{\sum\limits_{d = v}^{u} f_d} \]我们再设 \(sum_i\) 表示 \(f_i\) 的前缀和,\(sum_i = \sum\limits_{j = 1}^{i} f_i\),有
\[f_u = 1 + \frac{1}{out_u + 1}\sum\limits_{(u, v) \in R}(sum_u - sum_{v - 1}) \]因为 \(sum_u = sum_{u - 1} + f_u\),左右两边都有 \(f_u\) 不好转移。
所以我们将所有右边的 \(f_u\) 调到左边去。
我们先将两边同时乘以 \(out_u + 1\):
\[\begin{aligned} (out_u + 1)f_u &= out_u + 1 + \sum\limits_{(u, v) \in R}(sum_u - sum_{v - 1})\\ &= out_u + 1 + \sum\limits_{(u, v) \in R}(f_u + sum_{u - 1} - sum_{v - 1})\\ &= out_u + 1 + out_uf_u + \sum\limits_{(u, v) \in R}(sum_{u - 1} - sum_{v - 1})\\ (out_u + 1)f_u - out_uf_u &= out_u + 1 + \sum\limits_{(u, v) \in R}(sum_{u - 1} - sum_{v - 1})\\ f_u &= out_u + 1 + \sum\limits_{(u, v) \in R}(sum_{u - 1} - sum_{v - 1})\\ \end{aligned} \]这就是递推式,最终的答案就是 \(E_{1\rightarrow n + 1} = \sum\limits_{i = 1}^{n}E_{i\rightarrow i + 1} = sum_n\)。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1000010, MOD = 998244353;
int id, n, m;
int d[N], f[N], sum[N];
vector<int> edge[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> id >> n >> m;
for (int i = 1; i <= m; i++) {
int u, v;
cin >> u >> v;
d[u]++;
edge[u].push_back(v);
}
for (int i = 1; i <= n; i++) {
f[i] = d[i] + 1;
for (auto x : edge[i]) f[i] = (1ll * f[i] + sum[i - 1] - sum[x - 1]) % MOD;
sum[i] = (1ll * sum[i - 1] + f[i]) % MOD;
}
cout << (sum[n] % MOD + MOD) % MOD << '\n';
return 0;
}
参考文献
P2516 [HAOI2010] 最长公共子序列
思路
设 \(f_{i, j}\) 表示在第一个串 \(s1\) 的前 \(i\) 个字符和第二个串 \(s2\) 的前 \(j\) 个字符可以构成的最长公共子序列,设 \(p_{i, j}\) 表示方案数。
如果 \(s1_i\) 与 \(s2_j\) 相等,那么 \(f_{i, j} = f_{i - 1, j - 1} + 1, p_{i, j} = p_{i - 1, j - 1}\)。
如果 \(f_{i - 1, j}\) 大于 \(f_{i, j}\),那么 \(f_{i - 1, j}\) 与 \(p_{i - 1, j}\) 覆盖 \(f_{i, j}\) 与 \(p_{i, j}\),如果相等则 \(p_{i, j}\) 加上 \(p_{i - 1, j}\)。
如果 \(f_{i, j - 1}\) 大于 \(f_{i, j}\),那么 \(f_{i, j - 1}\) 与 \(p_{i, j - 1}\) 覆盖 \(f_{i, j}\) 与 \(p_{i, j}\),如果相等则 \(p_{i, j}\) 加上 \(p_{i, j - 1}\)。
如果到最后 \(f_{i - 1, j - 1}\) 与 \(f_{i, j}\) 相等,那么 \(p_{i, j}\) 要减去 \(p_{i - 1, j - 1}\),因为算重了。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 5010, MOD = 100000000;
char s1[N], s2[N];
int f[2][N], p[2][N];
int n, m;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> (s1 + 1) >> (s2 + 1);
n = strlen(s1 + 1) - 1;
m = strlen(s2 + 1) - 1;
for (int j = 0; j <= m; j++) p[0][j] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= m; j++) f[1][j] = p[1][j] = 0;
p[1][0] = 1;
for (int j = 1; j <= m; j++) {
if (s1[i] == s2[j]) f[1][j] = f[0][j - 1] + 1, p[1][j] = p[0][j - 1];
if (f[0][j] > f[1][j]) f[1][j] = f[0][j], p[1][j] = p[0][j];
else if (f[0][j] == f[1][j]) p[1][j] += p[0][j];
if (f[1][j - 1] > f[1][j]) f[1][j] = f[1][j - 1], p[1][j] = p[1][j - 1];
else if (f[1][j - 1] == f[1][j]) p[1][j] += p[1][j - 1];
if (f[1][j] == f[0][j - 1]) p[1][j] -= p[0][j - 1];
f[1][j] %= MOD, p[1][j] %= MOD;
}
for (int j = 0; j <= m; j++) f[0][j] = f[1][j], p[0][j] = p[1][j];
}
cout << (f[1][m] + MOD) % MOD << '\n' << (p[1][m] + MOD) % MOD << '\n';
return 0;
}
P5322 [BJOI2019] 排兵布阵
思路
设 \(f_{i, j}\) 表示在第 \(i\) 个城堡,总共派出去 \(j\) 人可以获得的最大分值。
我们将每个城堡的派遣人数进行排序,我们只有派遣比某个派遣人数的 \(2\) 倍大 \(1\) 才最划算。
所以有 \(f_{i, j} = \max\{f_{i - 1, j - a[i][k] \times 2 - 1} + i \times k)\}\)。
当然也可以不派人,\(f_{i, j} = f_{i - 1, j}\)。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 110, M = 20010;
int f[N][M];
int a[N][N];
int s, n, m;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> s >> n >> m;
for (int j = 1; j <= s; j++)
for (int i = 1; i <= n; i++)
cin >> a[i][j];
for (int i = 1; i <= n; i++) sort(a[i] + 1, a[i] + s + 1);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) f[i][j] = f[i - 1][j];
for (int j = 1; j <= m; j++) {
for (int k = 1; k <= s; k++) {
if (j - a[i][k] * 2 - 1 >= 0) f[i][j] = max(f[i][j], f[i - 1][j - a[i][k] * 2 - 1] + i * k);
}
}
}
cout << f[n][m] << '\n';
return 0;
}
P2051 [AHOI2009] 中国象棋
思路
设 \(f_{i, j, k}\) 表示考虑到了第 \(i\) 行,有 \(j\) 个只放了一个棋子的列,有 \(k\) 个放了两个棋子的列。
然后我们根据棋子数量的变化就可以写出:
\[f_{i, j, k} = f_{i - 1, j, k} + f_{i - 1, j - 1, k} \times (m - (j - 1) - k) + f_{i - 1, j + 1, k - 1} \times (j + 1) + \]\[f_{i - 1, j, k - 1} \times (m - j - (k - 1)) \times j + f_{i - 1, j + 2, k - 2} \times C_{j + 2}^2 + f_{i - 1, j - 2, k} \times C_{m - (j - 2) - k}^2 \]是不是非常简单呢?
代码
/*******************************
| Author: SunnyYuan
| Problem: P2051 [AHOI2009] 中国象棋
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P2051
| When: 2023-09-14 14:52:55
|
| Memory: 125 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
const int N = 110, MOD = 9999973;
int n, m;
int f[N][N][N];
int c[N][N];
void init() {
c[0][0] = 1;
for (int i = 1; i < N; i++) {
c[i][0] = 1;
for (int j = 1; j <= i; j++) c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % MOD;
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
init();
cin >> n >> m;
int ans = 0;
f[0][0][0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= m; j++) {
for (int k = 0; j + k <= m; k++) {
f[i][j][k] = f[i - 1][j][k];
if (j > 0) f[i][j][k] = (f[i][j][k] + 1ll * f[i - 1][j - 1][k] * (m - (j - 1) - k)) % MOD;
if (k > 0) f[i][j][k] = (f[i][j][k] + 1ll * f[i - 1][j + 1][k - 1] * (j + 1)) % MOD;
if (k > 0) f[i][j][k] = (f[i][j][k] + 1ll * f[i - 1][j][k - 1] * (m - j - (k - 1)) * j) % MOD;
if (k > 1) f[i][j][k] = (f[i][j][k] + 1ll * f[i - 1][j + 2][k - 2] * c[(j + 2)][2]) % MOD;
if (j > 1) f[i][j][k] = (f[i][j][k] + 1ll * f[i - 1][j - 2][k] * c[(m - (j - 2) - k)][2]) % MOD;
if (i == n) ans = (ans + f[i][j][k]) % MOD;
}
}
}
cout << ans << '\n';
return 0;
}