定义
给定一个网络,最大流就是求出在这个网络的所有流中流量最大的流。
Frod-Fulkerson
增广路
如果一个路径满足以下要求,那么它就是一个增广路:
- 其起点与终点分别是源点 \(S\) 和汇点 \(T\)。
- 对于这个路径中所有边 \(x\to y\) 的流量剩余容量 \(C_{x\to y}-f(x\to y)\ne 0\)。
求解方法
对于一种暴力的方法,我们可以一直寻找增广路知道寻找不到为止。在找到一条增广路之后,计算出路径上剩余容量的最小值 \(k\)。接着将路径上所有的剩余容量减少 \(k\) 再将网络的总流量也就是答案增加 \(k\) 就好了。
但是有一个问题,这样在某些情况下只能找到一些较优解:
显而易见的,如果使用 \(1\to 3\to 4\) 和 \(1\to 2\to 4\) 可以得到的流是 \(2\)。
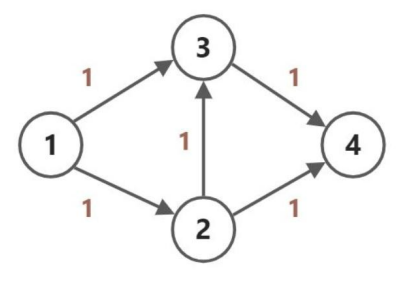
可是在使用直接 dfs 进行搜索之后,可能会得到一个为 \(1\to 2\to 3\to 4\) 的路径,这样得到的流就只有 \(1\) 了。
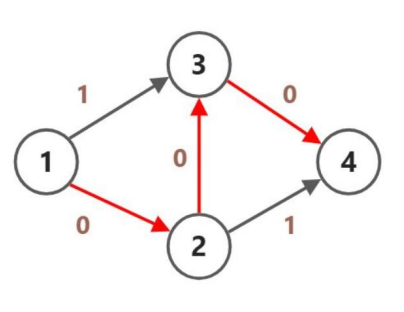
为了解决这个问题,我们可以考虑一种类似反悔贪心的手段避免上面情况发生。在每一次找到增广路时,在将这面走的剩余流量减少 \(k\) 的时候,同时将增广路的反边的剩余流量增加 \(k\)。
同样是上面的问题,在建出给定的网络之后我们又为每一条边建一个反边:
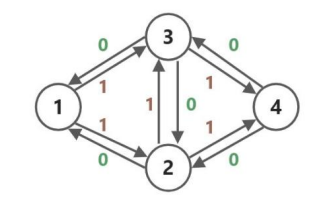
接着,在直接 dfs 得到一条增广路 \(1\to 2\to 3\to 4\) 之后,将原有的边与反边全部更新得到下图:
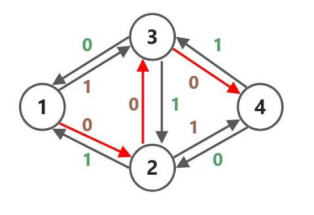
继续寻找新的增广路,得到 \(1\to 3\to 2\to 4\)。
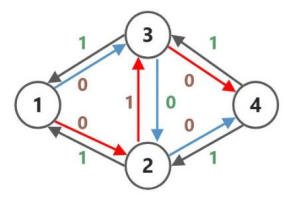
因为两次遍历及经过了 \(2\to 3\) 也经历的 \(3\to 2\) 所以它们的贡献就被抵消了,其效果与直接进行 \(1\to 3\to 4,1\to 2\to 4\) 是一样的。
在使用 dfs 不断寻找增广路知道不存在是,Frod-Fulkerson 算法就完成了,这个网络的最大流就是增广路的贡献。
假设流量为 \(\alpha\),那么其时间复杂度在最坏情况下为 \(O(\alpha\cdot (n+m))\),因为可能每一次增广路得到的 \(k\) 都是 \(1\)。
实现
bool bfs(int rGraph[V][V], int s, int t, int parent[])
{
bool visited[V];
memset(visited, 0, sizeof(visited))
queue<int> q;
q.push(s);
visited[s] = true;
parent[s] = -1;
// Standard BFS Loop
int u;
while (!q.empty())
{
// edge: u -> v
u = q.front(); // head point u
q.pop();
for (int v = 0; v < V; ++v) // tail point v
{
if (!visited[v] && rGraph[u][v] > 0) // find one linked vertex
{
q.push(v);
parent[v] = u; // find pre point
visited[v] = true;
}
}
}
return visited[t] == true;
}
int fordFulkerson(int graph[V][V], int s, int t)
{
int u, v,rGraph[V][V];
for (u = 0; u < V; ++u)
{
for (v = 0; v < V; ++v)
{
rGraph[u][v] = graph[u][v];
}
}
int parent[V],max_flow = 0;
while (bfs(rGraph, s, t, parent))
{
// edge: u -> v
int path_flow = INT_MAX;
for (v = t; v != s; v = parent[v])
{
// find the minimum flow
u = parent[v];
path_flow = min(path_flow, rGraph[u][v]);
}
// update residual capacities of the edges and reverse edges along the path
for (v = t; v != s; v = parent[v])
{
u = parent[v];
rGraph[u][v] -= path_flow;
rGraph[v][u] += path_flow; // assuming v->u weight is add path_flow
}
max_flow += path_flow;
}
return max_flow;
}
Edmonds-Karp
求解方法
简单的说,Edmonds-Karp 就是在 Frod-Fulkerson 的基础上,将栈改为了队列,或者说将 dfs 实现改为了 bfs 实现。虽然其表面上只是更改了实现方式,但是这也是为 Frod-Fulkerson 添加了一个优化:每次增广最短的增广路。这个优化其实很重要,因为在优化之后其最劣复杂度就被控制在了 \(O(nm^2)\)。
时间复杂度证明
在找到一条增广路之后,我们可定需要将可以压榨的全部榨干,也就是肯定有一条边被跑慢,我们定义这一条边为关键边。所以经过增广操作,这些边因为剩余流量为 \(0\) 所以在残余网络中就被无视掉了,也就是这一条增广路就断开了。所以我们每一次进行增广操作,其实就是破坏增广路。所以从 \(S\) 到 \(T\) 自然就会单调递增,也就保证了 bfs 搜索的正确性。
因为每一次将一条增广路破坏之后都至少有 \(1\) 条边被从残量网络中被删除,所以求解增广次数就可以与关键边的出现次数进行直接的联系。
因为关键边会从残量网络中消失,直到反向边上有了流量才会恢复成为关键边的可能性,而当反向边上有流量时最短路长度一定会增加。显而易见,增广路的长度肯定位于 \(1\) 到 \(m\) 之间,所以总共的增广次数为 \(nm\) 次。
因为在 Edmonds-Karp 中计算残量网络的方法为 bfs 其时间复杂度为 \(O(m)\),所以总共的时间复杂度就应该为 \(O(nm^2)\)。
实现
int Bfs() {
memset(pre, -1, sizeof(pre));
for(int i = 1 ; i <= n ; ++ i) flow[i] = INF;
queue <int> q;
pre[S] = 0, q.push(S);
while(!q.empty()) {
int op = q.front(); q.pop();
for(int i = 1 ; i <= n ; ++ i) {
if(i==S||pre[i]!=-1||c[op][i]==0) continue;
pre[i] = op; //找到未遍历过的点
flow[i] = min(flow[op], c[op][i]); // 更新路径上的最小值
q.push(i);
}
}
if(flow[T]==INF) return -1;
return flow[T];
}
int Solve() {
int ans = 0;
while(true) {
int k = Bfs();
if(k==-1) break;
ans += k;
int nw = T;
while(nw!=S) {//更新残余网络
c[pre[nw]][nw] -= k, c[nw][pre[nw]] += k;
nw = pre[nw];
}
}
return ans;
}
总结
虽然比起 Frod-Fulkerson 来说 Edmonds-Karp 已经优秀了许多,但是因为 \(m\) 一般为 \(n^2\) 级别,所以这个算法的之间复杂度其实是可以达到 \(O(n^5)\) 的级别,这依旧很难接受。
经过分析容易发现,在 Edmonds-Karp 求解了一次增广路之后它都要重新计算一次残量网络,十分耗费时间。如果可以将在一个网络中所有的增广矩阵在一次中全部求解出来在再进行增广操作,那么效果可能就会得到一个优化。
Dinic
分层图
我们可以定义一个叫分层图的概念:如果 \(S\) 到 \(x\) 的距离为 \(dis(S,x)=l\),那么点 \(x\) 位于第 \(l\) 层。
理论上的求解方法
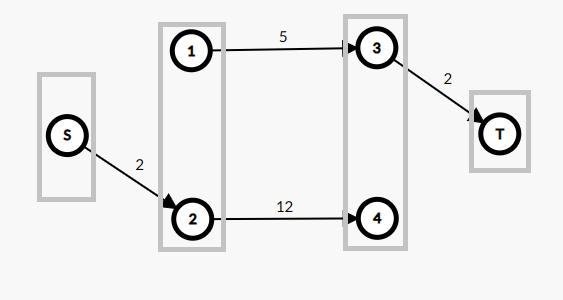
对于下方的这个网络,在所有边的边权均为 \(1\) 的情况下先跑一个最短路。
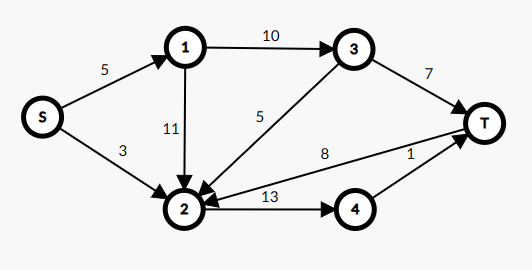
可以得到 \(dis(S,S)=0\),\(dis(S,1)=dis(S,2)=1\),\(dis(S,3)=dis(S,4)=2\),\(dis(S,T)=3\)。所以我们就把 \(S\) 分到第 \(0\) 层,\(1,2\) 分到第 \(1\) 层,\(3,4\) 分到第 \(2\) 层,\(T\) 单独分到第 \(3\) 层。
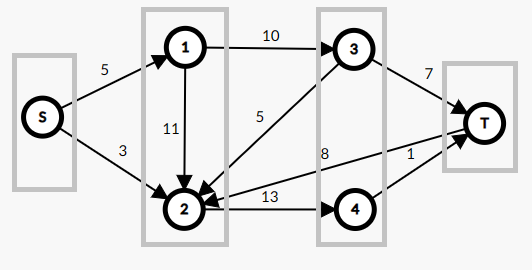
因为反向边都不在最短路上,所以我们可以将他们忽视。同时在一层中的路线对于最短路也是没有贡献的,所以将他们也删除。通过这些优化,得到下面的一张图。
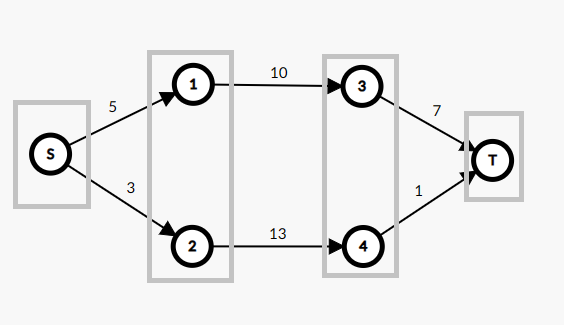
在分层结束之后,所有的剩余流量非 \(0\) 的边都在一个残量网络上,所以我们就可以使用 dfs 直接进行增广。但是反向边的剩余流量还是需要计算的,因为在将关键边的剩余流量设为 \(0\) 之后,dfs 可能还是会将贡献再次计算。
阻塞流
Dinic 的关键就是阻塞流,因为每次进行增广操作我们都会将所有的增广路,所以说与 Edmonds-Karp 算法一样,在进行了一次操作时候深度一样的所有增广路都被破坏了,就像下图。
先这样的破坏增广路,我们就称之为阻塞流。
理论上的时间复杂度
因为每一次操作都会将所有的增广路全部榨干,所以增广路的长度必然是严格递增的,所以一共只会进行 \(m\) 次增广操作。而对于 dfs,其时间复杂度为 \(O(n)\),所以总共的时间复杂度为 \(O(nm)\),十分优秀。
理论上的实现
int Dinic(int s,int t){
int ans=0;
while(BFS(s,t))
ans+=DFS(s,INF,t);
return ans;
}
int DFS(int s,int flow,int t){
if(s==t||flow<=0)
return flow;
int rest=flow;
for(Edge* i=head[s];i!=NULL&&rest>0;i=i->next){
if(i->flow>0&&depth[i->to]==depth[s]+1){
int k=DFS(i->to,std::min(rest,i->flow),t);
rest-=k;
i->flow-=k;
i->rev->flow+=k;
}
}
return flow-rest;
}
bool BFS(int s,int t){
memset(depth,0,sizeof(depth));
std::queue<int> q;
q.push(s);
depth[s]=1;
while(!q.empty()){
s=q.front();
q.pop();
for(Edge* i=head[s];i!=NULL;i=i->next){
if(i->flow>0&&depth[i->to]==0){
depth[i->to]=depth[s]+1;
if(i->to==t)
return true;
q.push(i->to);
}
}
}
return false;
}
dfs 函数中,\(s\) 表示现在的位置,\(t\) 表示汇点,而 \(flow\) 则表示因为上游所有流量的最小值,因为所有的流都满足 \(f(x\to y)\le C_{x\to y}\)。接着有一个局部变量 \(rest\),表示上游的流量限制还有 \(rest\) 单位没有下传。因为要满足流量守恒,我们只能把流入的流量分配到后面,所以这个 \(rest\) 实际上保存的就是最大可能的流入流量。最后返回的的 \(flow-rest\) 的意思就是在将所有的后继节点全部访问了之后一九无法排除的流,应该让答案减去这个这个贡献。
问题
在增广路的同时我们还面临了一个问题没使用阻塞 dfs 求解增广路其实与使用 bfs 求解的 Edmonds-Karp 完全不同,因为使用阻塞 dfs 会导致一些点需要重复计算,所以在写 dfs 的时候不可以打 \(vis\) 标记。
对于下图,在某些特定的流量设计下 \(3\) 好节点就一定需要多次访问。
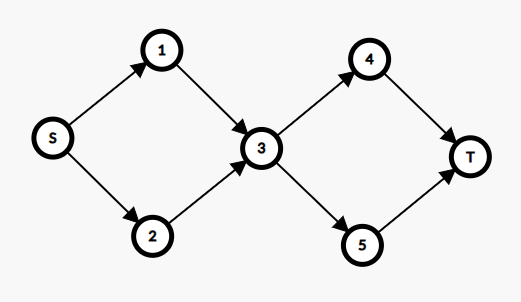
因为 dfs 不使用 \(vis\) 标记是指数级别的,所以我们需要进行一些优化。
实现
#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
#define int long long
using namespace std;
const int N=205,inf=0x3f3f3f3f3f3f3f3f;
struct node{int x,v,id;};
vector<node> v[N];
int n,m,s,t,dep[N],p[N];
void add(int x,int y,int val){
int sti=v[x].size(),edi=v[y].size();
v[x].push_back({y,val,edi});
v[y].push_back({x,0,sti});
}
bool bfs(){
queue<int> q;
memset(dep,-1,sizeof(dep));
memset(p,0,sizeof(p));
q.push(s),dep[s]=0;
while(!q.empty()){
int top=q.front();q.pop();
for(node i:v[top]){
if(dep[i.x]==-1&&i.v){
dep[i.x]=dep[top]+1;
q.push(i.x);
}
}
}
return dep[t]!=-1;
}
int dfs(int x,int flow){
if(x==t){
return flow;
}
for(int i=p[x];i<v[x].size();i++){
p[x]=i;
int to=v[x][i].x,len=v[x][i].v;
if(dep[x]+1==dep[to]&&len){
int t=dfs(to,min(len,flow));
if(t){
v[x][i].v-=t;
v[to][v[x][i].id].v+=t;
return t;
}
else{
dep[to]=-1;
}
}
}
return 0;
}
int dinic(){
int ans=0,flow;
while(bfs()){
while(flow=dfs(s,inf)){
ans+=flow;
}
}
return ans;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n>>m>>s>>t;
for(int i=1,x,y,val;i<=m;i++){
cin>>x>>y>>val;
add(x,y,val);
}
cout<<dinic()<<'\n';
return 0;
}
真实的求解
首先需要明确,将 \(dep_x\) 设置为 \(-1\) 就是将其删除的意思,因为不可能有 \(dep\) 为 \(-2\) 的节点。因为如果尝试给我们忽略掉的点推送一个非 \(0\) 的流量,那么他一定只会返回 \(0\),一点用都没有。
然后最关键的决定时间复杂度的优化是当前弧优化,我们每次向某条边的方向推流的时候,肯定要么把推送量用完了,么是把这个方向的容量榨干了。
除了最后一条因为推送量用完而无法继续增广的边之外其他的边一定无法继续传递流量给 \(t\) 了。这种无用边会在寻找出边的循环中增大时间复杂度,必须删除。
最后再看重新这一整个 DFS 的过程,如果当前路径的最后一个点可以继续扩展,则肯定是在层间向汇点前进了一步,最多走 \(V\) 步就会到达汇点. 在前进过程中,我们发现一个点无法再向 \(t\) 传递流量,我们就删掉它. 根据我们在分析EK算法时间复杂度的时候得到的结论,我们会找到 \(O(E)\) 条不同的增广路,每条增广路又会前进或后退 \(O(V)\) 步来更新流量,又因为我们加了当前弧优化所以查找一条增广路的时间是和前进次数同阶的,于是单次阻塞增广 DFS 的过程的时间上界是 \(O(VE)\) 的.
于是 Dinic 算法的总时间复杂度是 \(O(V^2E)\) 的。
标签:最大,增广,int,复杂度,flow,网络,流量,dfs From: https://www.cnblogs.com/liudagou/p/18298170