定义
上下界网络流就是在原本网络流的基础上添加了每一条边流量的上界 \(r(x\to y)\) 和下界 \(l(x\to y)\),也就是说 \(f(x\to y)\) 必须满足 \(l(x\to y)\le f(x\to y)\le r(x\to y)\)。
无源汇上下界可行流
无源汇界网指的是没有源点和汇点但是每一个点的出边与入边都满足流量守恒的网络。在这个网络的流量方案中,应使得第 \(i\) 条边的流量位于 \([l_i,r_i]\) 之间。
换而言之流量 \(f(x\to y)\) 必然满足 \(l(x\to y)\le f(x\to y)\le r(x\to y)\),而普通的网络流只满足 \(0\le f(x\to y)\le C_{x\to y}\)。
所以根据不等式的性质,我们可以得到 \(0\le f(x\to y)-l(x\to y)\le r(x\to y)-l(x\to y)\),于是上下界网络流就被转化为了普通网络流。
但是这样求解的网络的流量不一定是守恒的,就像下面的情况:
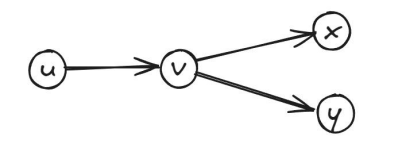
对于普通网络流,设 \(f_{in}(v)\) 表示流入 \(v\) 的流量,\(f_{out}(v)\) 表示流出 \(v\) 的流量,所以有 \(f_{in}(v)=f_{out}(v)\)。在经过修改之后,\(f_{in}(v)\) 变为了 \(f_{in}'(v)=f_{in}(v)-l(u\to v)\),而 \(f_{out}(v)\) 变为了 \(f_{out}'(v)=f_{out}-l(v\to x)-l(v\to y)\)。因为并不知道 \(l(v\to x)+l(v\to y)\) 是否等于 \(l(u\to v)\),所以无法确定流量是守恒的。
#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
#define int long long
using namespace std;
const int N=2e5+5,inf=0x3f3f3f3f3f3f3f3f;
struct node{int x,v,id;};
vector<node> v[N];
int n,m,s,t,dep[N],p[N];
void add(int x,int y,int val){
int sti=v[x].size(),edi=v[y].size();
v[x].push_back({y,val,edi});
v[y].push_back({x,0,sti});
}
bool bfs(){
queue<int> q;
memset(dep,-1,sizeof(dep));
memset(p,0,sizeof(p));
q.push(s),dep[s]=0;
while(!q.empty()){
int top=q.front();q.pop();
for(node i:v[top]){
if(dep[i.x]==-1&&i.v){
dep[i.x]=dep[top]+1;
q.push(i.x);
}
}
}
return dep[t]!=-1;
}
int dfs(int x,int flow){
if(x==t||!flow){
return flow;
}
for(int i=p[x];i<v[x].size();i++){
p[x]=i;
int to=v[x][i].x,len=v[x][i].v;
if(dep[x]+1==dep[to]&&len){
int t=dfs(to,min(len,flow));
if(t){
v[x][i].v-=t;
v[to][v[x][i].id].v+=t;
return t;
}
else{
dep[to]=-1;
}
}
}
return 0;
}
int dinic(){
int ans=0,flow;
while(bfs()){
ans+=dfs(s,inf);
}
return ans;
}
int a[N],f[N],cnt[N];
vector<int> ask;
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n>>m,t=n+1;
for(int i=1,x,y,l,r;i<=m;i++){
cin>>x>>y>>l>>r;
a[i]=l,f[x]-=l;f[y]+=l;
add(x,y,r-l),ask.push_back(x);
}
int sum=0;
for(int i=1;i<=n;i++){
if(f[i]>0){
add(s,i,f[i]),sum+=f[i];
}
if(f[i]<0){
add(i,t,-f[i]);
}
}
if(dinic()!=sum){
cout<<"NO\n";
}
else{
cout<<"YES\n";
for(int i=1;i<=m;i++){
cout<<a[i]+v[v[ask[i-1]][cnt[ask[i-1]]].x][v[ask[i-1]][cnt[ask[i-1]]].id].v<<'\n';
// cout<<ask[i-1]<<' '<<v[ask[i-1]][cnt[ask[i-1]]].x<<'\n';
cnt[v[ask[i-1]][cnt[ask[i-1]]].x]++;
cnt[ask[i-1]]++;
}
}
return 0;
}
有源汇上下界可行流
为了保证流量守恒,如果 \(f_{in}'(v)<f_{out}'(v)\),那么就新建一个源点 \(S\) 到 \(v\) 的容量为 \(f_{out}'(v)-f_{in}'(v)\) 来弥补流量的不足。反之如果 \(f_{in}'(v)>f_{out}'(v)\),那么就同理建一个从 \(v\) 到汇点 \(T\) 的容量为 \(f_{in}'(v)-f_{out}'(v)\) 来帮助 \(v\) 排除多出的流量。
因为流量守恒,所以我们新连的边一定要跑满,即求解新的网络的最大流是否等于所有 \(S\) 的出边的容量的和。定义可行流的流量是残留网络的反向边的大小加上减去的下界 \(l\),注意这是残留网络,反向边的流量大小是原图的流量。
在有源汇网络上求一个流量方案,使得第 \(i\) 条边的流量必须在 \([l_i,r_i]\) 之间,且除源汇外每个点流量守恒。
假设源点为 \(S\),汇点为 \(T\)。则入一条 \(T\) 到 \(S\) 的上界为无穷大,下界为 \(0\) 的边转化为无源汇上下界可行流问题。
若有解,则 \(S\) 到 \(T\) 的可行流流量等于T到S的附加边的流量。
有源汇上下界最大/小流
首先求出一个有源汇有上下界可行流,然后将附加边删除后,在残量网络上跑源点到汇点的最大流,\(\text{有源汇上下界最大流}=\text{可行流}+\text{第二次跑的源点到汇点的最大流}\)。
再跑一次最大流是因为附加网络上属于原图的边还有流量没被“榨干”。容易发现只要附加网络上不属于原图的边满流,那么属于原图的边怎么跑流量都是守恒的。因为第一次跑最大流已经保证所有点守恒,第二次跑最大流不会经过不属于原图的边,因此等价于对原图跑一次普通的最大流,除源汇外流量守恒。两次合起来总流量一定守恒,这就保证了正确性。
同理求最小流就跑一次汇点到源点的最大流,\(\text{有源汇上下界最大小流}=\text{可行流}-\text{第二次跑的汇点到源点的最大流}\)。这是因为反向边的流量增加等价于正向边的的流量减少。
#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
using namespace std;
const int N=3e5+5,inf=0x3f3f3f3f;
struct node{int x,v,id;};
vector<node> v[N];
int n,m,s,t,dep[N],p[N];
void add(int x,int y,int val){
int sti=v[x].size(),edi=v[y].size();
v[x].push_back({y,val,edi});
v[y].push_back({x,0,sti});
}
bool bfs(){
queue<int> q;
memset(dep,-1,sizeof(dep));
memset(p,0,sizeof(p));
q.push(s),dep[s]=0;
while(!q.empty()){
int top=q.front();q.pop();
for(node i:v[top]){
if(dep[i.x]==-1&&i.v){
dep[i.x]=dep[top]+1;
q.push(i.x);
}
}
}
return dep[t]!=-1;
}
int dfs(int x,int flow){
if(x==t){
return flow;
}
for(int i=p[x];i<v[x].size();i++){
p[x]=i;
int to=v[x][i].x,len=v[x][i].v;
if(dep[x]+1==dep[to]&&len){
int t=dfs(to,min(len,flow));
if(t){
v[x][i].v-=t;
v[to][v[x][i].id].v+=t;
return t;
}
else{
dep[to]=-1;
}
}
}
return 0;
}
int dinic(){
int ans=0,flow;
while(bfs()){
while(flow=dfs(s,inf)){
ans+=flow;
}
}
return ans;
}
int a[N],f[N],cnt[N],S,T;
vector<int> ask;
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n>>m>>S>>T;
t=n+1;
for(int i=1,x,y,l,r;i<=m;i++){
cin>>x>>y>>l>>r;
a[i]=l,f[x]-=l;f[y]+=l;
add(x,y,r-l),ask.push_back(x);
}
int sum=0;
for(int i=1;i<=n;i++){
if(f[i]>0){
add(s,i,f[i]),sum+=f[i];
}
if(f[i]<0){
add(i,t,-f[i]);
}
}
add(T,S,inf);
if(dinic()!=sum){
cout<<"please go home to sleep\n";
}
else{
int ans=v[S][v[S].size()-1].v;
for(int i=1;i<=n;i++){
if(f[i]>0){
v[s].pop_back();
v[i].pop_back();
}
if(f[i]<0){
v[i].pop_back();
v[t].pop_back();
}
}
v[S].pop_back();
v[T].pop_back();
s=T,t=S;
cout<<ans-dinic()<<'\n';
}
return 0;
}