最多限制相交路径
问题
已知一些路径,每一个节点可以属于多个路径,但是属于路径的数量不得超过一个给定的上限。
解决方法
将 \(1\) 个节点拆为 \(2\) 个,接着进行连边,其中容量代表可以经过的路径。
最大权闭合图
定义
如果一个点集满足其中任意元素可以到达的所有元素都在集合中,那么这个点集中的节点可以经过的边和节点构成的图被称为闭合图。最大权闭合图指对于所有的闭合图,点权和最大的图就是最大权闭合图。
对于下图,最大权闭合图为 \(\{2,4,5\}\),其权值为 \(6\)。
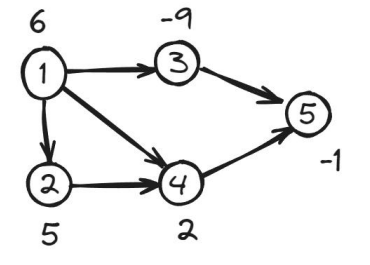
求解方法
新建源点 \(S\) 与汇点 \(T\),让 \(S\) 向所有点权为正的节点连一条容量为点权的边,接着让所有点权为负的点向 \(T\) 连一条容量为点权的绝对值的边。在将图中原有的边设为无穷大之后,求出最小割。
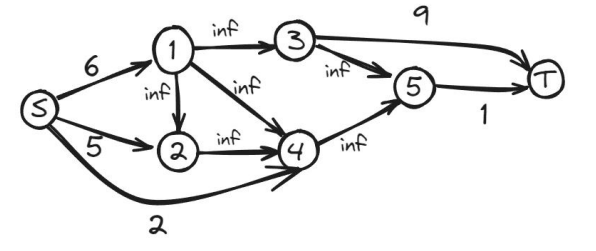
有定理:\(\text{最大权闭合图}=\text{所有正点权和}-\text{最小割}\)。
证明
通过上述方式构造,最小割中的所有边均与 \(S\) 或者 \(T\),因为其他的点均被设置为了无穷大,肯定不会选择。
假设在删除割之后,\(S\) 可以到大的点为图 \(A\),在图 \(A\) 中删除与 \(S\) 相连的边与 \(S\) 节点后构成的图 \(A'\) 就是一个最大权闭合图。
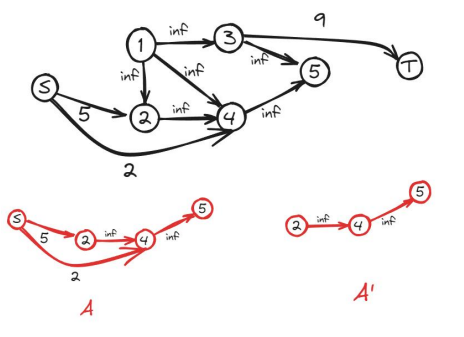
设割集中,连接到点 \(S\) 的点权和为 \(x_1\),连接到点 \(T\) 的点权和为 \(x_2\),割集的和为 \(X=1+x_2\)。设图 \(A'\) 所有点的点权和为 \(W\),其中正权和为\(w_1\),负权和为\(-w_2\),有\(W=w_1+w_2\)。
则 \(W+X=w_1-w_2+x_1+2\),其中 \(w_2=c_2\),因为图 \(A'\) 所有负权点都连接到 \(T\),而为了保证 \(A'\) 中的点都不与 \(T\) 连通,这些负权点与 \(T\) 相连的边都删除了,在割集中。
得到 \(W+X=w_1+1\),移项有 \(W=(w_1+x_1)-X\),其中 \(w_1+x_1\) 为所有正权点之和,要想 \(W\) 最大,那么 \(X\) 最小,则 \(X\) 为最小割。
最小点权覆盖集
问题
在图中选取一些点,满足图中每条边连接的两个点中,至少一个被选择,求所选取的点最小权值和。
求解方法
首先对图进行二分染色,将点分为左部分和右部分。新建源点 \(S\) 和汇点 \(T\),\(S\) 向左部节点连边,容量为点权,右部向 \(T\) 连边,容量为点权,图中原有边的容量设为无穷大。对新图求解最小割就是最小点权覆盖集。
证明
对于任意一条从 \(S\) 到 \(T\) 的路径,一定存在一条边被割断,而且因为原图对应的边容量为无穷大,因此割边必然存在于 \(S\) 与左部节点之间或者右部节点与 \(T\) 之间,对应的流量便是选取的最小点权。
在图中选取一些点,满足图中每条边连接的两个点中,至多一个被选择,求所选取的点最大权值和。
定理:\(\text{最大权独立集}=\text{所有点权值和}-\text{最小点权覆盖集}\)
标签:所有,text,模型,常见,最小,闭合,点权,节点 From: https://www.cnblogs.com/liudagou/p/18298173证明:因为点权覆盖集对于原图的点集的补集即为点权独立集,而点集的点权之和为常数,所以当点权覆盖集最小时,点权独立集最大,对应的答案即为所有点权值和-最小点权覆盖集。