论文提出了经典的Vision Transormer模型Swin Transformer,能够构建层级特征提高任务准确率,而且其计算复杂度经过各种加速设计,能够与输入图片大小成线性关系。从实验结果来看,Swin Transormer在各视觉任务上都有很不错的准确率,而且性能也很高
来源:晓飞的算法工程笔记 公众号
论文: Swin Transformer: Hierarchical Vision Transformer using Shifted Windows

Introduction
长期以来,计算机视觉建模一直由卷积神经网络(CNN)主导。从AlexNet在ImageNet中的革命性表现开始,通过更大的规模、更广泛的连接以及更复杂的卷积形式逐级演变出越来越强大的CNN架构。另一方面,自然语言处理(NLP)网络架构的演变则采取了不同的路径,如今最流行的就是Transformer架构。Transformer专为序列建模和转导任务而设计,以使用注意力来建模数据中的长距离关系而著称。
Transformer在语言领域的巨大成功促使研究人员研究其在计算机视觉的适应性,目前也取得了很不错的结果,特别是用于图像分类的ViT以及用于视觉语言联合建模的CLIP。
本文作者尝试扩展Transformer的适用性,将其用作计算机视觉的通用主干,就像Transformer在NLP和CNN在视觉中所做的那样。将Transformer在语言领域的高性能表现转移到视觉领域所面临的主要挑战,主要源自两个领域之间的差异:
- 尺寸。token作为NLP Transformer中的基本元素,其尺寸是固定的,对应段落中的一个单词。但视觉目标的尺寸可能有较大的差异,这也是如物体检测等任务备受关注的问题,通常需要捕获多尺度特征来解决。而在现有的基于Transformer的模型中,token都是固定尺寸的,对应一个单词或固定的图片区域,显然不适用于当前的视觉应用任务。
- 数量级。与文本段落中的单词数量相比,图像中的像素数量要多很多。在许多如语义分割的视觉任务中,需要进行像素级的密集预测。而Transformer在高分辨率图像上的处理是难以进行的,因为自注意力的计算复杂度与图像大小成二次方关系。
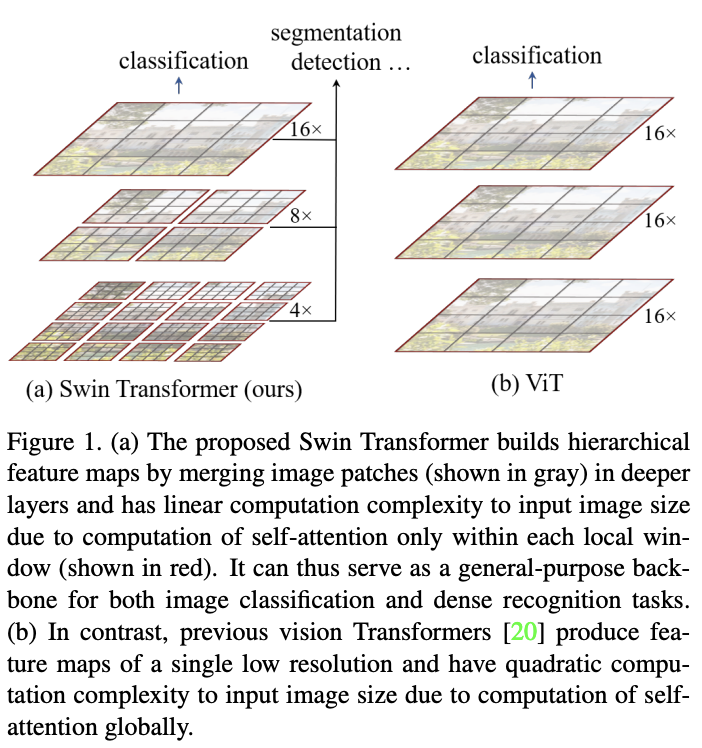
为了解决这些问题,论文提出了Swin Transformer,能够构建层级特征图并且计算复杂度与图像大小成线性关系。
基于层级特征图,Swin Transformer模型可以很方便地结合先进的密集预测技术,如特征金字塔网络(FPN)或U-Net。如图1a所示,Swin Transformer从小尺寸的图像块开始,逐渐合并相邻图像块来构建层级特征。线性计算复杂度则是通过只在局部非重叠窗口(图1a红色区域)计算自注意力来实现的。由于窗口大小是固定的,所以复杂度与图像大小成线性关系。
Swin Transformer还有一个关键设计元素,就是在连续的同尺度self-attention层使用移位窗口分区(shifted window partition)。类似于对分组卷积的分组间通信优化,移位窗口能够促进前一层的窗口之间的特征融合,从而显著提高建模能力。常见的基于滑动窗口(sliding window)的自注意力,由于每个query对应的key集不同,所以都要单独计算注意力矩阵然后输出,实现上很低效。而移位窗口由于仅在窗口内进行自注意力计算,同窗口内的query对应的key集相同,key集可在窗口内共享,可直接单次矩阵计算同时完成全部注意力计算然后输出,在实现上十分高效。
Swin Transformer在图像分类、目标检测和语义分割的识别任务上取得了很不错的结果。在速度相似的情况下,准确率显著优于ViT/DeiT和ResNe(X)t模型。在COCO test-dev数据集上达到的58.7 box AP和51.1 mask AP,分别比SOTA高2.7和2.6。在ADE20K val数据集集上获得了 53.5 mIoU,比SOTA高3.2。在ImageNet-1K数据集上达到了87.3%的top-1准确率。
Method
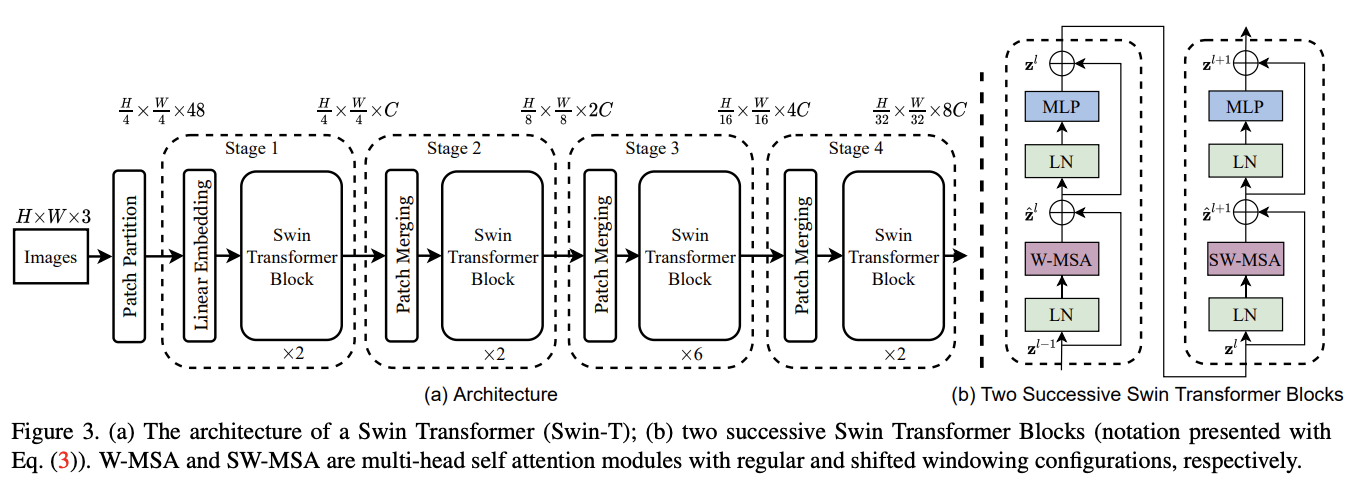
Overall Architecture
Swin Transformer整体架构如图3所示,该图是Tiny版本Swin-T,分为以下几个部分:
- Patch Partition:输入图像的处理跟ViT类似,通过patch splitting模块将输入的RGB图像分割成不重叠的图像块,直接将每个图像块内的RGB值concate起来作为一个token。在实现时,每个图像块的大小为\(4\times 4\),因此每个图像块的特征维度为\(4\times 4\times 3 = 48\)。
- Linear Embedding:随后,Linear Embedding层对这个原始特征进行处理,将其映射到指定维度大小\(C\)。
- Swin Transformer block:在得到图像块token后,连续使用多个包含改进自注意力的Transformer模块(Swin Transformer block)进行特征提取。
- Patch Merging:为了构建层级特征,随着网络变深,通过Patch Merging层减少token的数量。第一个Patch Merging层将每个维度的\(2\times 2\)的相邻图像块特征concate起来,并在得到的\(4C\)维特征上使用Linear Embedding层进行维度映射。这样,token量就减少了\(2\times 2 = 4\)的倍数(相当于两倍下采样)并且映射到指定维度大小\(2C\),最后同样使用Swin Transformer blocks进行特征变换。
Linear Embedding与后续的Swin Transformer blocks一起称为Stage 1,token的数量为\(\frac{H}{4}\times \frac{W}{4}\)。第一个Patch Merging和Swin Transformer blocks称为Stage 2,分辨率保持在\(\frac{H}{8}\times \frac{W}{8}\)。该过程重复两次,分别为Stage 3和Stage 4,输出分辨率分别为\(\frac{H}{16}\times \frac{W}{16}\)和\(\frac{H}{32}\times \frac{W}{32}\)。各Stage共同构建的层级特征,其特征分辨率与典型卷积网络相同,例如VGG和ResNet。因此,Swin Transformer架构可以方便地替换现有方法中的骨干网络,用于各种视觉任务。
-
Swin Transformer block
Swin Transformer模块将Transformer模块中的多头自注意力(MSA)替换为基于windows或shifted window的多头自注意力,其他层保持不变。如图3b所示,对于连续的Swin Transformer模块,前一个使用基于window的MSA模块,后一个使用基于shifted window的MSA模块,然后都是接一个带GELU非线性激活的两层MLP,每个MSA模块和每个MLP都有LayerNorm(LN)层和一个残差连接。
Shifted Window based Self-Attention
标准的Transformer架构及其在图像分类的应用都进行全局自注意力计算,计算每个token和所有其他token之间的关系。全局自注意力计算的复杂度是token数量的二次方,这显然不适用于许多需要大量token进行密集预测或产生高分辨率图像的视觉问题。
-
Self-attention in non-overlapped windows
为了高效计算,论文提出仅在局部窗口内计算自注意力,各窗口以不重叠的方式均匀地划分图像。假设每个窗口包含\(M\times M\)个图像块,在包含\(h\times w\)个图像块的特征图上,全局模式和窗口模式的计算复杂度分别为:
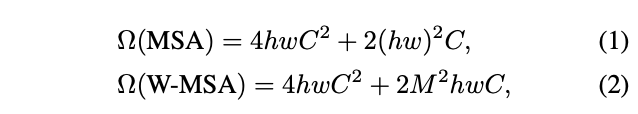
复杂度前面的部分应该是Q、K、V和最终输出的生成计算,后面部分是Q和K的矩阵相乘和权值与V的相乘。全局模式的计算复杂度与图像块数量\(hw\)成二次方,而当\(M\)固定时(默认设置为7),窗口模式的计算复杂度则是线性的。所以当\(hw\)很大时,全局自注意力计算通常是难以进行的,而基于窗口的自注意力则是可调整的。
-
Shifted window partitioning in successive blocks
类似于分组卷积的问题,基于窗口的自注意力缺乏跨窗口的连接,限制了建模能力。为了在保持高效计算的情况下引入跨窗口连接,论文提出了移位窗口分区(shifted window partitioning)方法,在连续的Swin Transformer模块交替使用两种不同分区逻辑。
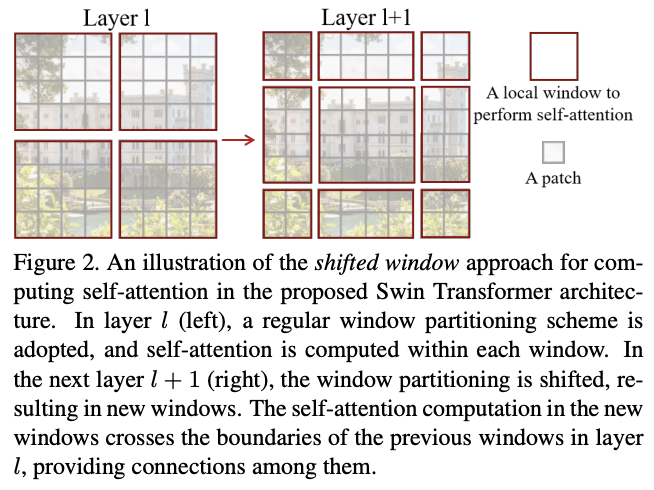
如图2所示,第一个模块使用从左上角像素开始的常规窗口分区策略,将\(8\times 8\)特征图均匀地划分为4个\(4\times 4\)(M = 4)大小的窗口。然后,下一个模块采用与前一层不同的窗口分区策略,将常规窗口移动\((\lfloor \frac{M}{2}\rfloor, \lfloor \frac{M}{2}\rfloor)\)个像素。
基于移位窗口分区方法,连续的Swin Transformer模块的计算变为:

其中\(\hat{z}^l\)和\(z^l\)表示\(l\)层的(S)WMSA模块和MLP模块的输出特征,W-MSA和SW-MSA 分别表示使用常规窗口分区和移位窗口分区的窗口多头自注意。
移位窗口分区方法增加了上一层中相邻的非重叠窗口之间的联系,这在图像分类、物体检测和语义分割中是十分有效的。
-
Efficient batch computation for shifted configuration
移位窗口分区会导致窗口数变多,从\((\lfloor \frac{M}{2}\rfloor, \lfloor \frac{M}{2}\rfloor)\)个窗口变为\((\lfloor \frac{h}{M}+1\rfloor, \lfloor \frac{w}{M}+1\rfloor)\)个窗口,而且部分窗口的大小会小于\(M\times M\)。在计算窗口自注意力时,一般会将多个窗口拼接成矩阵进行矩阵计算,要求每个窗口的大小一致。
一个简单的移位窗口分区的兼容做法是将较小的窗口填充到\(M\times M\)的大小,然后在计算注意力时屏蔽掉填充的值。在常规分区中的窗口数量较少时,例如\(2\times 2\),使用这种简单的解决方案增加的计算量是相当大的(\(2\times 2 \to 3\times 3\),增加2.25倍)。
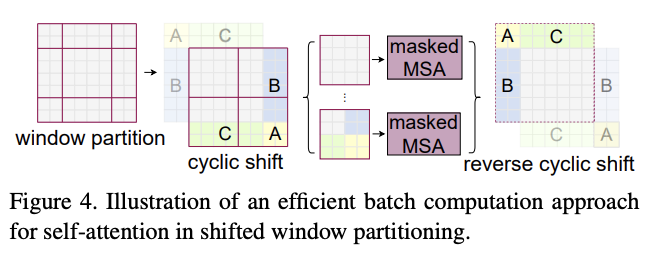
为此,论文提出了一种更高效的批处理计算方法,通过向左上方向循环移位进行小窗口的合并计算,如图4所示。在移位之后,单个窗口可能由几个原本不相邻的子窗口组成,因此需要采用掩码机制将自注意力计算限制在每个子窗口内,掩码机制主要是屏蔽掉计算出来的注意力矩阵。在循环移位后,由于窗口数量与常规窗口分区的数量相同,因此计算量也相当。
-
Relative position bias
在计算self-attention时,论文参考当前一些研究的做法,在进行相似度计算时为每个head加入相对位置偏置(relative position bias) \(B\in \mathbb{R}^{M^2\times M^2}\),注意区别于常规相对位置编码的做法:
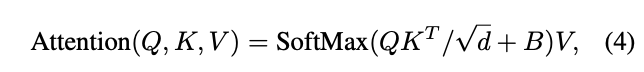
其中\(d\)是Q、K、V特征的维度,\(M^2\)是窗口中的图像块数。由于每个轴方向的相对位置均在\([−M + 1, M −1]\)范围内,论文设置了一个较小尺寸的可学习偏置矩阵\(\hat{B}\in \mathbb{R}^{(2M−1)\times(2M−1)}\)(对应二维相对位置组合数量),然后根据窗口中各位置的相对位置转换得到唯一索引编码,从\(\hat{B}\)取对应的值构成\(B\)矩阵。这样做的目的有两个,降低参数量(\((2M−1)\times(2M−1)\) vs \((M^2\times M^2)\)),同时让相同位置的使用相同偏置。
从实验结果来看,与没有此偏置项或使用绝对位置偏置的对比,相对位置偏置有显著的性能提升。ViT使用了绝对位置偏置,论文也尝试进一步叠加绝对位置偏置,但测试会略微降低性能,因此在实现中未采用它。
当要fine-tuning不同窗口大小的模式时,预训练到的相对位置偏置也可通过bi-cubic interpolation进行转换。
Architecture Variants
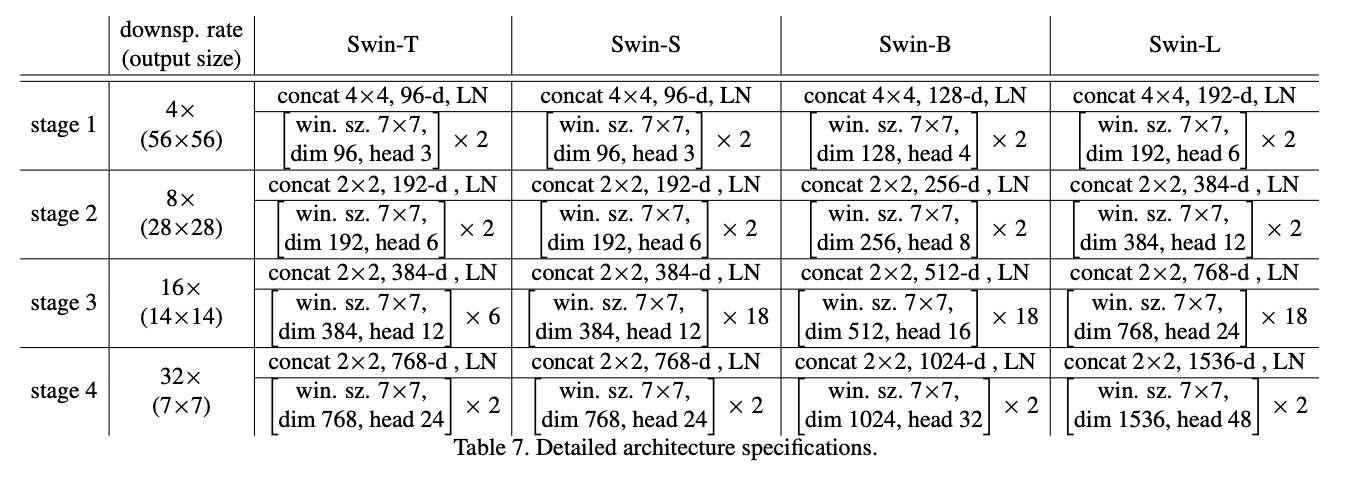
论文构建了基础模型Swin-B,跟ViTB/DeiT-B的模型大小和计算复杂度差不多。此外,论文还涉及了Swin-T、Swin-S和Swin-L版本,分别是基础模型的模型大小和计算复杂度的0.25倍、0.5倍和2倍的版本。其中,Swin-T和Swin-S的复杂度分别对标ResNet-50(DeiT-S)和ResNet-101。默认情况下,窗口大小设置为 M = 7。对于所有实验,自注意力计算每个head的特征维度\(d = 32\),每个MLP的扩展层\(α = 4\)。
这些模型变体的架构超参数是:
- Swin-T:C = 96, layer numbers =
- Swin-S:C = 96, layer numbers =
- Swin-B:C = 128, layer numbers =
- Swin-L:C = 192, layer numbers =
其中\(C\)是Stage 1的维度数。
Experiment
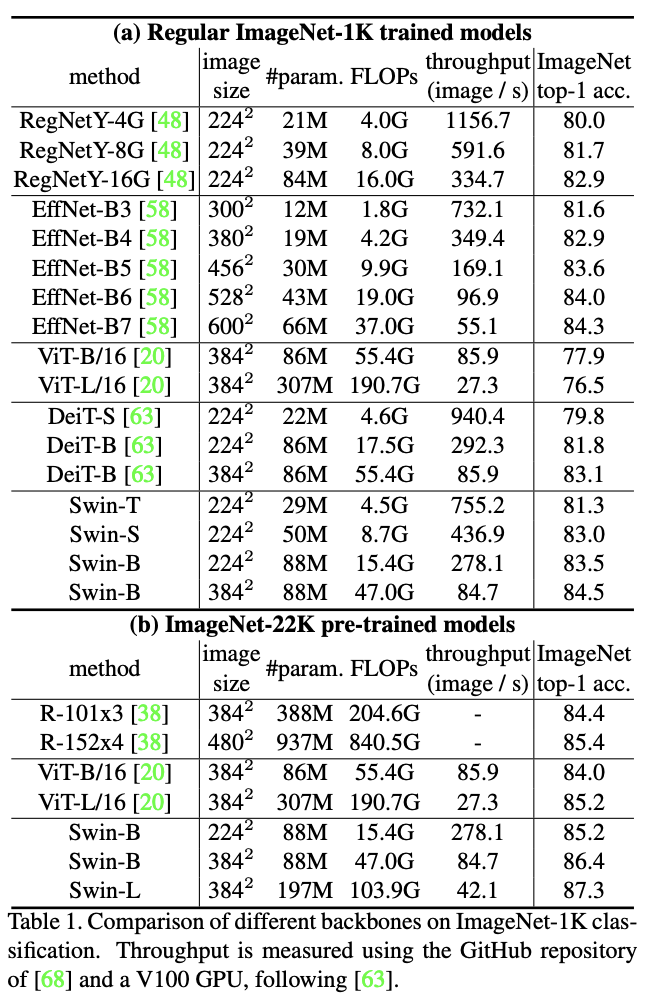
直接训练和预训练在Image-1K数据集上的性能对比。
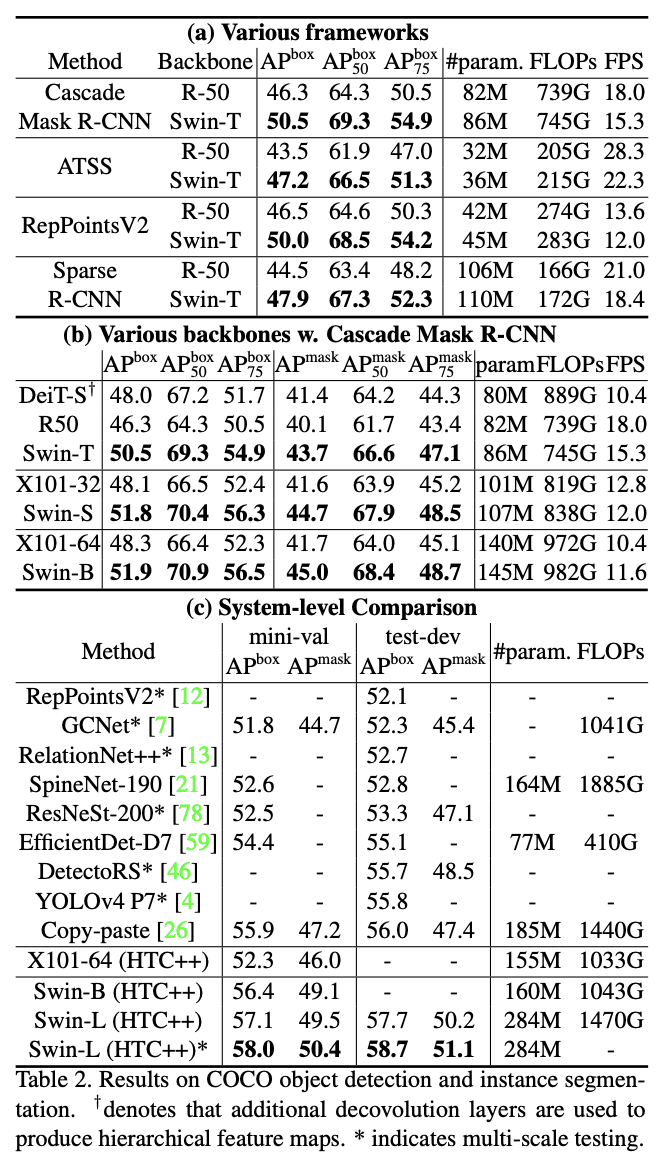
目标检测上对比嵌套多种检测算法和其它主干网络。
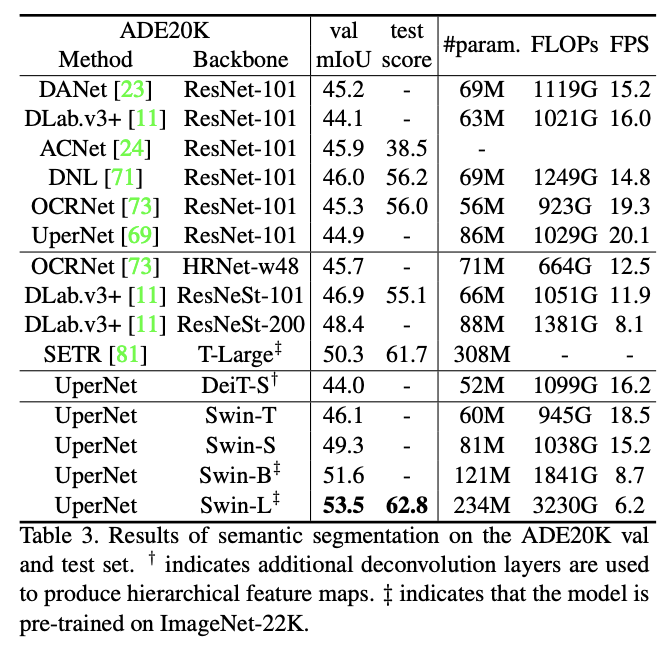
语义分割上对比其它SOTA模型。
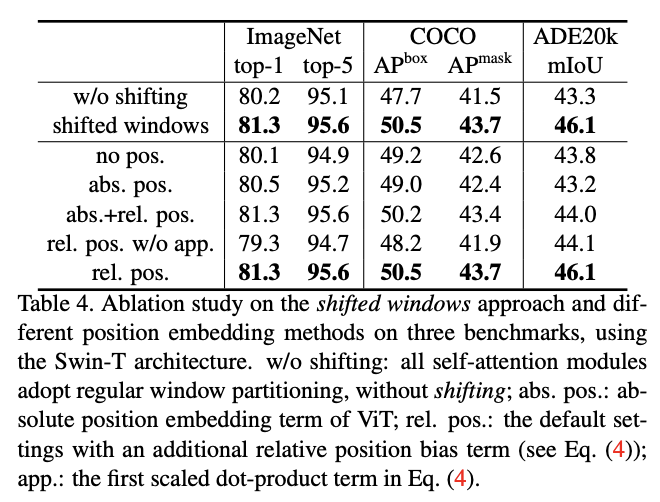
移位窗口策略性能以及不同的position embedding组合的对比。
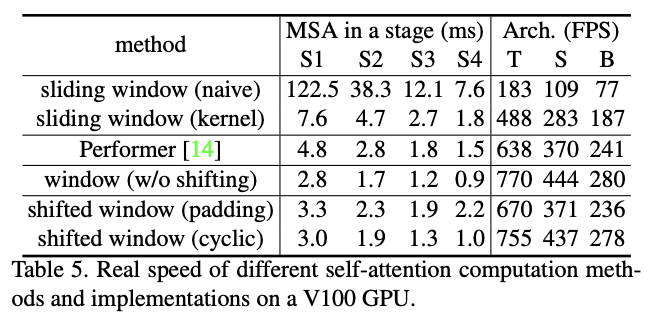
不同策略之间的推理性能对比。
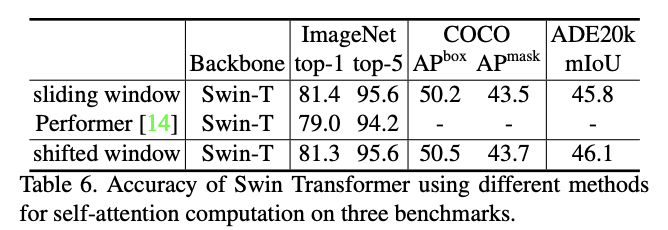
Swin Transformer搭配不同自注意力计算方法的性能对比。
Conclusion
论文提出了经典的Vision Transormer模型Swin Transformer,能够构建层级特征提高任务准确率,而且其计算复杂度经过各种加速设计,能够与输入图片大小成线性关系。从实验结果来看,Swin Transormer在各视觉任务上都有很不错的准确率,而且性能也很高。
如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】
