斜率优化 dp
适用条件
在单调队列优化 dp 中常见转移方程中,如果 \(cost(i,j)\) 多项式包含 \(i, j\) 乘积项,则可以化成一次函数维护斜率解决。
以P5785 [SDOI2012] 任务安排为模板,主要记录如何斜率优化
转移方程为(不多赘述)
\[f_i = \min_{0≤j<i}\{f_j + S \times (sc_n - sc_j) + st_i \times (sc_i - sc_j)\} \]提出式子中含有单独 \(i\) 的常量:\(f_i = st_i\times sc_i + S \times sc_n + \min\bigg(f_j - S \times sc_j - st_i \times sc_j\bigg)\)
考察 \(min\) 函数内部的 多项式:\(f_j - sc_j \times (S + st_i)\)
该式子中,有 \(i \times j\) 的项,因此不能直接用上一章节中提到的滑动窗口来维护一个前缀的最值,但是分析的思想可以继承,含 \(i\) 的项是一个常量,故该多项式就能够抽象成如下形式:
注意,这里的 变量1 和 变量2 并不是两个独立变量(该函数非多元函数)
变量1 \(f_j\) 是与 \(j\) 有关的 变量,变量2 \(sc_j\) 也是与 \(j\) 有关的 变量
因此,不妨令 \(\begin{cases} f_j = y(j) \\\\ sc_j = x(j) \\\\ k = S+st_i \end{cases}\),则该函数可以化为:\(y(j) - k \cdot x(j)\)
把 \(y(j)\) 写成 \(y\),\(x(j)\) 写成 \(x\)
求 \(y - kx ~ (0 \le j \lt i)\) 函数的极值问题,可以直观想到直线的斜截式方程:\(y = kx + b\)
对直线的斜截式方程进行变形:\(b = y - kx\)
要求 \(y - kx ~ (0 \le j \lt i)\) 函数的极值,就是求一个点 \((x_j, y_j)\) 与当前 \(k_i\) 构成的所有直线中,y 轴截距最小
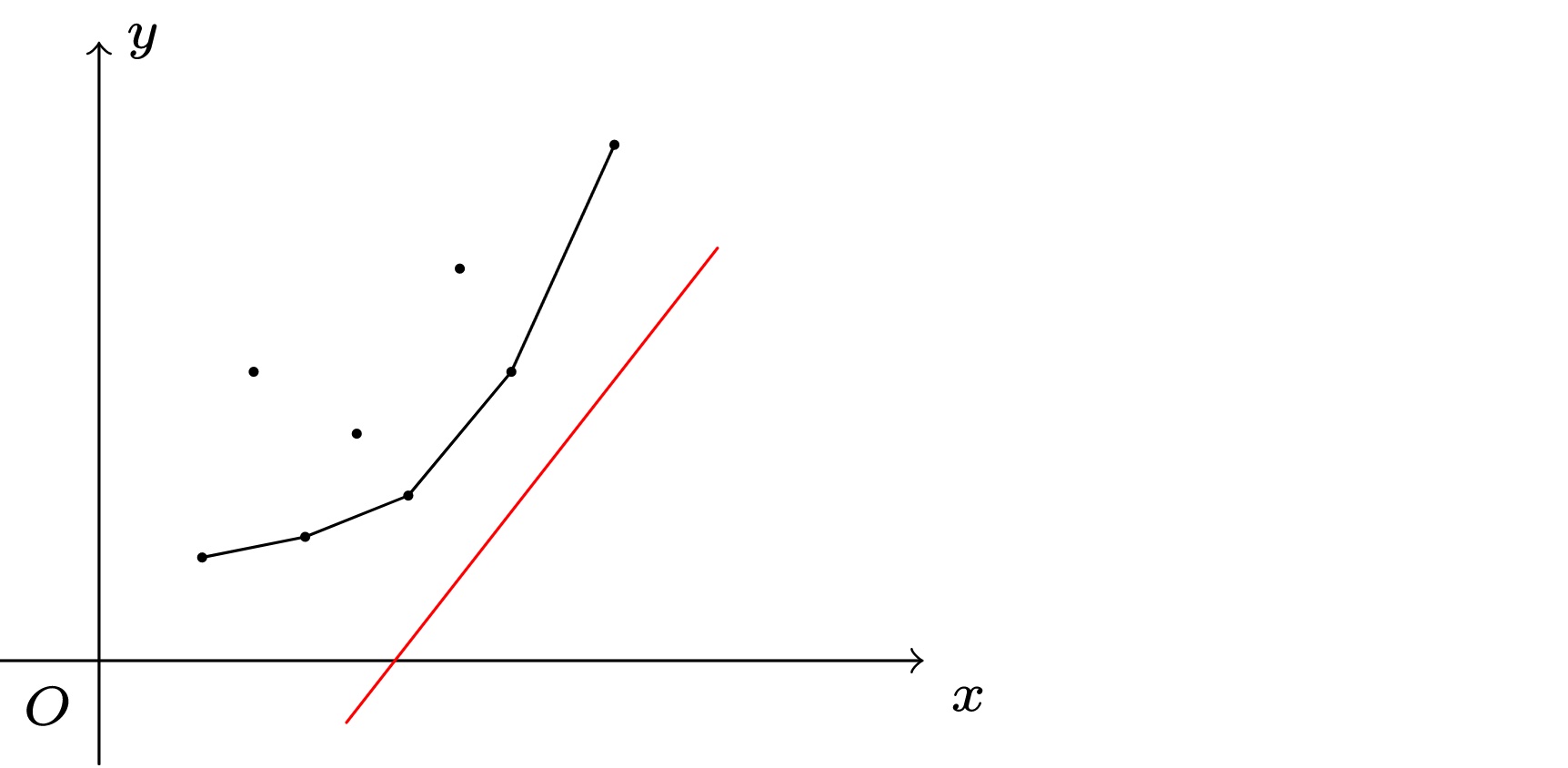
图中,黑色点 为所有 \(0 \le j \lt i\) 的点 \((x_j,y_j)\),红色线 为 斜率 是 \(k_i\) 的 某一条直线
从下往上(截距从小到大)去逼近当前所有的点
则 第一个 出现在直线上的点,就是满足 \(b_i = y_j - kx_j\) 的 最小截距 \(b_i\),即是当前阶段 DP 的 最佳策略
那么,如何有效的维护点集呢?
这就是一个线性规划的问题了:在点集中,找到一个点,绘制固定斜率的直线,使得截距最小
由线性规划知识可知:只用考虑点集中凸壳上的点即可,几何直观上,显然这题要维护的是下凸壳
因此,对于任意的 \(f_i\) 来说,我们只需去寻找下凸壳上的点构成直线 的最小截距即可
这样时间复杂度在最坏的情况下,还是 \(O(n^2)\)(即所有点的 \((x,y)\) 单增,全部点构成一个下凸壳)
直线方程中,各参数的性质
由于 \(t_i, c_i\) 都是 正整数,故他们的 前缀和 \(st_i,sc_i\) 是 单调递增的
对应于 直线方程的参数:\(x_j = sc_j\) 是 单调递增 的,\(k_i = S + st_i\) 也是 单调递增的
而下凸壳中相邻两点 构成的直线 斜率也是单调递增的
则下凸壳中第一个出现在直线上的点,满足:\(k_{j-1, j} \le k_i \lt k_{j,j+1}\),此时 直线截距 \(b_j\) 最小

而又由于 \(k_i\) 单调递增,所以 \(j\) 之前的点都不会是点集中出现在直线上的第一个点
此时只需维护点集区间 \([j,i]\) 的点即可,直到 \(k_{j,j+1} \le k \lt k_{j+1,j+2}\) 时,维护点集区间 变为 \([j+1,i]\)
根据上述所说,出现了我们最熟悉的模型-滑动窗口模型。
故我们可以直接利用 单调队列 来维护 下凸壳中的有效点集
并用队头的 两个元素 维护 大于当前斜率 \(k_i\) 的最小斜率 \(k_{q_{hh}~,~q_{hh+1}}\)
这里我把公式展开,方便大家理解:
把点插入单调队列前,先要队列中至少有两个点,然后把满足 \(k_{q_{tt-1}~,~q_{tt}} \ge k_{q_{tt}~,~i}\) 的 点 \(q_{tt}\) 弹出
即新加入的点,必须和原点集构成下凸壳,无效点要先删去,把公式展开:
这样,队列中相邻两点之间构成的直线斜率单增,也就是我们的有效下凸壳点集
时间复杂度: \(O(n)\)
#include <bits/stdc++.h>
#define rint register int
#define int long long
#define endl '\n'
using namespace std;
const int N = 3e5 + 5;
int n, s;
int t[N], c[N]; //时间、费用的前缀和数组
int f[N]; //设 f[i] 表示前 i 个任务分成若干批执行的最小费用
int q[N];
signed main()
{
cin >> n >> s;
//预处理前缀和
for (rint i = 1; i <= n; i++)
{
cin >> t[i] >> c[i];
t[i] += t[i - 1];
c[i] += c[i - 1];
}
//初始化
memset(f, 0x3f, sizeof f);
f[0] = 0;
//斜率优化 dp
int l = 0, r = 0; //0 也是一种方案,最开始队列中有一个 0
q[0] = 0;
for (rint i = 1; i <= n; i++)
{
//注意,由于每条线段需要两个点构成,所以队列中至少需要存在两个元素
while (l < r && f[q[l + 1]] - f[q[l]] <= (s + t[i]) * (c[q[l + 1]] - c[q[l]])) l++;
/*
乘法是移项的结果
但是如果乘法会爆 long long
则换回除法
因为好像乘法比除法精度高一点点
*/
int j = q[l];
f[i] = f[j] - (s + t[i]) * c[j] + t[i] * c[i] + s * c[n]; //状态转移方程
while(l < r && (f[q[r]] - f[q[r - 1]]) * (c[i] - c[q[r]]) >= (f[i] - f[q[r]]) * (c[q[r]] - c[q[r - 1]])) r--;
q[++r] = i;
}
cout << f[n] << endl;
return 0;
}
CF311 Cats Transport
对于每只猫,设 $a[i] = T[i] - \sum_{1≤j≤H[i]}{ D[j] } $。一名饲养员如果想接到第 \(i\) 只小猫,就必须在 \(a[i]\) 时刻及以后从 \(1\) 号山出发,若出发时刻为 \(t\),则这只猫的等待时间为 \(t - a[i]\)
把 \(a[i]\) 从小到大排序,求出排好序的 \(a\) 数组的前缀和,记录在数组 \(s\) 中,根据贪心策略,每个饲养员带走的猫一定是按照 \(a\) 排序后连续的若干只,毕竟早结束的小猫需要越早接,不然等待的时间只会越多。
设 \(f[i][j]\) 表示前 \(i\) 个饲养员带走前 \(j\) 只小猫,猫等待的时间总和最小值
假设第 \(i\) 个饲养员带走第 $ k + 1$ ~ $ j$ 只小猫,那么该饲养员的最早出发时间就是 \(a[j]\),这些猫的等待时间之和就是
\(\sum_{k + 1 ≤ p ≤ j}{ a[j] - a[p] } = a[j] * (j - k) - (s[j] - s[k])\)
得出状态转移方程:
\[f[i][j] = \min_{0 ≤ k < j}{ f[i - 1][k] + a[j] * (j - k) - (s[j] - s[k]) } \]把外层循环 \(i\) 看作定值,\(j\) 是状态变量,\(k\) 是决策变量,方程中存在乘积项 \(a[j] * k\),应考虑是用斜率优化,去掉
\(min\) 函数,对方程进行移项,\(f[i - 1][k] + s[k] = a[j] * k + f[i][j] - a[j] * j + s[j]\)
以 \(k\) 为横坐标,\(f[i - 1][k] + s[k]\) 为纵坐标建立平面直角坐标系,上式是一条以 \(a[j]\) 为斜率,\(f[i][j] - a[j] * j + s[j]\)
为截距的直线,当截距最小化时,\(f[i][j]\) 取到最小值。
在最小化截距的线性规划问题中,应维护一个下凸壳,建立一个单调队列,队列中相邻两个决策 \(k1\) 和 \(k2\) 应满足 \(k1 < k2\) 并且
“斜率” \(((f[i - 1][k2] + s[k2]) - (f[i - 1][k1] + s[k1])) / (k2 - k1)\) 单调递增,因为直线斜率 a[j] 也已从小到大排序,
所以就是一个非常经典的斜率优化 \(dp\)。
对于每个状态变量 \(j\):
- 检查队头的两个决策变量
q[l]和q[l + 1],若斜率((f[i - 1][q[l + 1]] + s[q[l + 1]) - (f[i - 1][q[l]] + s[q[l]])) / (q[l + 1] - q[l]) <= a[j],则把q[l]出队,并继续检查新的队头 - 直接取队头
k = q[l]为最优决策,执行状态转移,计算出f[i][j] - 把新决策
j从队尾插入,在插入之前,若三个决策点k1 = q[r - 1], k2 = q[l], k3 = j不满足斜率单调递增
(不满足下凸性,即k2是无用决策),则直接从队尾把q[r]出队,并继续检查队尾
时间复杂度 \(O(PM)\)
P3571 [POI2014] SUP
设 \(f_i\) 表示为当前一次操作最多访问 \(i\) 个未访问的点的最小操作次数,\(s_i\) 表示表示深度\(\geqslant i\)的节点个数,有
\(f_i=max(j+ \lceil \frac{s_{j+1}}{i} \rceil)\)
若 \(i\) 是最优决策, \(∀j\neq i\), \(i+\lceil\dfrac{s_{i+1}}k\rceil\geq j+ \lceil\dfrac{s_{j+1}}k\rceil\)。变形得 \(i-j \geq \lceil\dfrac{s_{j+1}-s_{i+1}}k\rceil\)。深度为横坐标,纵坐标为 \(s_{x+1}\),当 \(j<i\) 时,\(\dfrac{s_{i+1}-s_{j+1}}{i-j}\geq -k\),当 \(j>i\) 时,\(\dfrac{s_{i+1}-s_{j+1}}{i-j}\leq -k\),发现斜率递减。
对 \((i,s_i)\) 建出上凸包,当 \(-k\) 递减,顶点会向横坐标大的方向移动,指针维护。
复杂度 \(\mathcal{O}(n)\)
CF1179D Fedor Runs for President
子树大小为 \(sz_i\),该路径上不同子树之间的点相互访问的简单路径增加了一条,增加路径数 \(\sum_{i∈path} {(n-sz_i)*sz_i} = \frac{1}{2} (n^2- \sum sz_i^2)\)
要求 \(\sum sz_i\) 的最小值
寻找性质,发现路径的两端必定为叶子或者根,若不为叶子,让他的端点向子树方向扩展,那么得到 \(sz_i\) 更小
\(f[i]\) 表示以 \(i\) 为根的子树中 \(\sum sz[i]\) 最小的链,转移方程为
\[f[i]=\min_{j∈son(i)}\{f[j]+(sz[i]-sz[j])^2\} \]对于根 \(s\),可以将 \(i,j\) 和并
\[ans=\min_{j∈son(i)}\{ans,f[i]+f[j]+(n-sz[i]-sz[j])^2\} \]将 \(s\) 与 \(i\) 合并,\(ans=\min_{j∈son(i)}\{f[i]+(n-sz[i])^2\}\),斜率优化,式子变为 \(f[j] + (n - sz[j]) ^ 2 = 2 * sz[i] * (n - sz[j]) + ans - sz[i] ^ 2 - f[i]\),以 \(n-sz[j]\) 为 \(x\) 轴,以 \(f[j] +(n-sz[j])^2\) 为 \(y\) 轴,单调队列维护斜率即可。
CF1083E The Fair Nut and Rectangles
两个矩形包含的充要条件是 \(x_i>x_j\) 且 \(y_i<y_j\)。\(x\) 升序,\(y\) 一降序。
\(f_i\) 表示考虑到第 \(i\) 个的答案。枚举上一个矩形,有转移方程
\[f_i = \min _{j<i}\left\{f_j -y_i *\left(x_i-x_j\right)\right\} \]非常朴实的一个转移方程,符合我们开头说的那种,\(y\) 递减,也就是决策点单调,单调队列维护。
复杂度 \(O(n \log n)\)。
备注:对于第一个题目的题目分析来源于 ycx2010 巨佬
标签:sz,直线,tt,斜率,hh,sc,优化,dp From: https://www.cnblogs.com/spaceswalker/p/18262017