基本技巧——哈夫曼树 学习笔记
概念
一棵包含有 \(n\) 个叶子节点的 \(k\) 叉树,其中第 \(i\) 个叶子节点带有权值 \(W_i\)。
树的带权路径长度,定义为从根结点到各叶结点的路径长度与相应叶节点权值的乘积之和。
树的带权路径长度,记为 WPL(Weighted Path Length of Tree),公式表示:
\[\text{WPL}=\sum_{i=1}^nW_iL_i \]在一组有确定权值的叶子节点中,可以构造出不同的 \(k\) 叉树。
其中,WPL 最小的 \(k\) 叉树,称为 \(k\) 叉哈夫曼树(Huffman 树)。
哈夫曼算法
容易发现,对于哈夫曼树,权值越小离根越远,反之,权值越大深度越小。
因此,容易得出,仅有叶子节点的度为 \(0\),其他节点的度均为 \(k\)。
证明:如果其他节点的度小于 \(k\),那么意味着下面的节点放到这个空位,结果更优。
因此,我们需要额外添加一些权值为 \(0\) 的叶子节点,使得叶子节点个数 \(n\) 满足,
\[n-1\equiv0\pmod{k-1} \]这样,我们就可以保证空的位置,会放在叶子上而不是非叶子节点,使得贪心正确。
算法流程
-
初始化:将给定的 \(n\) 个叶子节点,直接连到根上,共 \(n+1\) 个节点。
-
合并:从二叉树中选取两个权值和最小的节点,合并为一个新的节点。
-
重复合并操作,直至只剩 \(k-1\) 个节点,所得二叉树即为哈夫曼树。
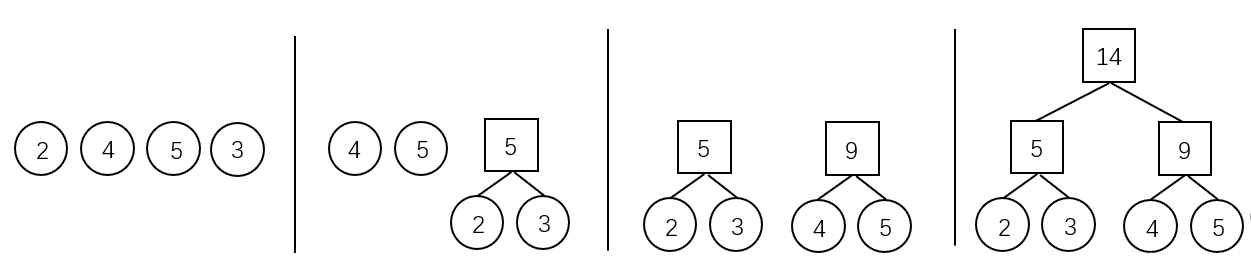
如果需要所得的最长编码最短,则还需要优先合并当前层数少的节点。
模板题
模板题,模拟即可,
#include <bits/stdc++.h>
using namespace std;
constexpr int N = 1e5 + 10;
using ll = long long;
struct emm {
ll w; int h;
emm() = default;
emm(ll w, int h): w(w), h(h) {}
friend bool operator <(const emm &a, const emm &b) {
return a.w == b.w ? a.h > b.h : a.w > b.w;
}
};
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
int n, k; cin >> n >> k; priority_queue<emm> heap;
ll w; for (int i = 1; i <= n; ++i) cin >> w, heap.emplace(w, 1);
while ((heap.size() - 1) % (k - 1) != 0) heap.emplace(0, 1);
ll ans = 0; auto merge = [&] {
int h = 0; ll w = 0;
for (int i = 1; i <= k; ++i) h = max(h, heap.top().h), w += heap.top().w, heap.pop();
ans += w, heap.emplace(w, h + 1);
};
while (heap.size() >= k) merge();
cout << ans << endl << heap.top().h - 1 << endl;
return 0;
}
简单题
容易发现,合并顺序即叶子节点的深度,于是哈夫曼编码。
权值小的节点优先合并即可,代码:
#include <bits/stdc++.h>
using namespace std;
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
int n; cin >> n;
priority_queue<int, vector<int>, greater<int>> d;
for (int i = 0, x; i < n; ++i) cin >> x, d.push(x);
int ans = 0;
while (d.size() > 1) {
int a = d.top(); d.pop();
int b = d.top(); d.pop();
ans += a + b, d.push(a + b);
}
cout << ans << endl;
return 0;
}