一、分块
概念与作用
1.概念:将数列等分为若干个不相交的区间,每一个区间称为一个块。
2.作用:优化算法,降低复杂度。
分块入门1
题面:
给出一个长为n的数列,以及n个操作,操作涉及区间加法,单点查询。
分析:
将n个元素等分成若干块,比如\(\{1,4,8,2,9,6,3,7,5\}\),等分成3块,则第一块包含的数据为\(\{1,4,8\}\),第二、三块以此类推。我们给每一个块加一个加法标记,对于每次的区间\([l,r]\)加法操作,直接对块进行标记叠加。
\(l,r\)必然不一定是块的边界,也就意味着左右端点可能在块的中间,直接一个个暴力增加。设块的元素个数为m,标记块个数至多\(\frac{n}{m}\)个,暴力增加元素个数至多2m个,时间复杂度:\(O(\frac{n}{m})+O(m)\),根据均值不等式,可证明\(m=\sqrt n\)时存在最低复杂度。故我们以下所有分块大小均默认为\(\sqrt n\)。询问就很轻松了,直接返回元素的值加上所在区间的标记。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 50005;
int n, a[N], x, b[N], tag[N];
//a[i]表示第i个数是多少
//x表示每个块中有几个数(即大小)
//b[i]表示第i个数在第几个块中
//tag[i]表示第i个块整体增加的值
inline void add(int l, int r, int w) {
//判断r是否和l在同一个块里,取范围较小的增加
for (rg int i = l; i <= min(b[l] * x, r); i++) {
a[i] += w;
}
if (b[l] != b[r]) { //如果l和r不在同一个块里
//从r所在块的开始一直到r进行增加
for (rg int i = (b[r] - 1) * x + 1; i <= r; i++) {
a[i] += w;
}
}
//如果这一整个块都要增加,不要一一去更新,对整个块的标记增加
//对从l之后的一个块到r前面的一个块的标记增加
for (rg int i = b[l] + 1; i <= b[r] - 1; i++) {
tag[i] += w;
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int opt, l, r, w;
cin >> n;
x = sqrt(n);
for (rg int i = 1; i <= n; i++) {
cin >> a[i];
}
for (rg int i = 1; i <= n; i++) {
b[i] = (i - 1) / x + 1;
}
for (rg int i = 1; i <= n; i++) {
cin >> opt >> l >> r >> w;
if (opt) cout << a[r] + tag[b[r]] << "\n"; //查询a[r]的值
else add(l, r, w); //对a[l]到a[r]增加w
}
return qwq;
}
/*
4
1 2 2 3
0 1 3 1
1 0 1 0
0 1 2 2
1 0 2 0
5
2
*/
分块入门2
题面:
给出一个长为n的数列,以及n个操作,操作涉及区间加法,询问区间内小于某个值x的元素个数。
分析:
有了上一题的经验,我们可以发现,数列简单分块问题实际上有三项东西要我们思考:
对于每次区间操作:
1.不完整的块的\(O(\sqrt n)\)个元素怎么处理?
2.\(O(\sqrt n)\)个整块怎么处理?
3.要预处理什么信息?
我们先来思考只有询问操作的情况,不完整的块枚举统计即可;而要在每个整块内寻找1小于一个值的元素数,我们不得不要求块内元素是有序的,这样我们就能用二分法对块内查询。我们需要预处理时每块做一遍排序,复杂度\(O(nlogn)\),每次查询在\(\sqrt n\)个二分块内,以及暴力\(2\sqrt n\)个元素,总复杂度\(O(nlogn+n\sqrt nlog\sqrt n)\)。
那么区间加怎么办呢?套用第一题的办法,维护一个加法标记,略有区别的是,不完整的块修改后可能会使得该块内数字乱序,所以头尾两个不完整块需要重新排序。
在加法标记下的询问操作,块外还是暴力,查询小于(x-加法标记)的元素个数,块内用(x-加法标记)作为二分的值即可。
需要注意的点是,对于每次的区间修改,左右端点所在的块会因修改而不再呈升序排列,需要重新维护。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 5e4 + 5;
int n, x;
int a[N], b[N], tag[N];
vector<int> v[505]; //维护每个块中包含哪些数
inline void resort(int o) { //对o这个块重新排序
v[o].clear();
for (rg int i = (o - 1) * x + 1; i <= min(o * x, n); i++) {
v[o].push_back(a[i]);
}
sort(v[o].begin(), v[o].end());
}
inline void add(int l, int r, int w) {
//左半块暴力加
for (rg int i = l; i <= min(b[l] * x, r); i++) a[i] += w;
//对左半块重新排序
resort(b[l]);
if (b[l] != b[r]) {
//右半块暴力加
for (rg int i = (b[r] - 1) * x + 1; i <= r; i++) a[i] += w;
//对右半块重新排序
resort(b[r]);
}
for (rg int i = b[l] + 1; i <= b[r] - 1; i++) tag[i] += w; //完整的块打标记
}
inline int query(int l, int r, int w) {
rg int ans = 0;
for (rg int i = l; i <= min(b[l] * x, r); i++) {
if (a[i] + tag[b[l]] < w) ans++; //左半块暴力
}
if (b[l] != b[r]) {
for (rg int i = (b[r] - 1) * x + 1; i <= r; i++) {
if (a[i] + tag[b[r]] < w) ans++;
}
}
for (rg int i = b[l] + 1; i <= b[r] - 1; i++) {
rg int x = w - tag[i];
//返回第一个大于等于x的位置
ans += lower_bound(v[i].begin(), v[i].end(), x) - v[i].begin();
}
return ans;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int opt, l, r, w;
cin >> n;
x = sqrt(n);
for (rg int i = 1; i <= n; i++) cin >> a[i];
for (rg int i = 1; i <= n; i++) {
b[i] = (i - 1) / x + 1;
//将每个块包含的值存贮起来
v[b[i]].push_back(a[i]);
}
//对每个块进行排序
for (rg int i = 1; i <= b[n]; i++) sort(v[i].begin(), v[i].end());
for (rg int i = 1; i <= n; i++) {
cin >> opt >> l >> r >> w;
if (opt) cout << query(l, r, w * w) << "\n"; //询问[l,r]中小于w^2的个数
else add(l, r, w); //将[l,r]中的数都加w
}
return qwq;
}
/*
4
1 2 2 3
0 1 3 1
1 1 3 2
1 1 4 1
1 2 3 2
3
0
2
*/
分块入门3
题面:
给出一个长为n的数列,以及n个操作,操作涉及区间加法,询问区间内小于某个值x的前驱。
分析:
这一题在上一题的基础上稍作变化,将询问操作变为求某一个数在某一个区间内的前驱。
一个数的前驱定义为小于这个数的第一个数。这里要提到一点就是在每一个块中可以通过维护其他的数据结构来实现一些其他的操作。
这里维护一个不可重集合set。
对于查询,定义一个迭代器(指针)。set是有序的所以不需要排序,二分查找x。那么x前面的第一个数就是它的前驱。
显然,如果\(x=l\),那x就没有前驱。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long
using namespace std;
const int N = 1e5 + 5;
int n, x, a[N], tag[1001], b[N];
set<int> block[1001];
inline void add(int l, int r, int w) {
for (rg int i = l; i <= min(r, b[l] * x); i++) {
block[b[l]].erase(a[i]);
a[i] += w;
block[b[l]].insert(a[i]);
}
if (b[l] != b[r]) {
for (rg int i = (b[r] - 1) * x + 1; i <= r; i++) {
block[b[r]].erase(a[i]);
a[i] += w;
block[b[r]].insert(a[i]);
}
}
for (rg int i = b[l] + 1; i <= b[r] - 1; i++) tag[i] += w;
}
inline int query(int l, int r, int w) {
rg int ans = -1;
for (rg int i = l; i <= min(b[l] * x, r); i++) {
if (a[i] + tag[b[i]] < w) ans = max(ans, a[i] + tag[b[l]]);
}
if (b[l] != b[r]) {
for (rg int i = (b[r] - 1) * x + 1; i <= r; i++) {
if (a[i] + tag[b[r]] < w) ans = max(ans, a[i] + tag[b[r]]);
}
}
for (rg int i = b[l] + 1; i <= b[r] - 1; i++) {
rg int s = w - tag[i];
set<int>::iterator it = block[i].lower_bound(s); //定义正向迭代器
if (it == block[i].begin()) continue;
it--;
ans = max(ans, *it + tag[i]);
}
return ans;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int opt, l, r, w;
cin >> n;
x = sqrt(n);
for (rg int i = 1; i <= n; i++) cin >> a[i];
for (rg int i = 1; i <= n; i++) {
b[i] = (i - 1) / x + 1;
block[b[i]].insert(a[i]);
}
for (rg int i = 1; i <= n; i++) {
cin >> opt >> l >> r >> w;
if (opt) cout << query(l, r, w) << "\n";
else add(l, r, w);
}
return qwq;
}
/*
4
1 2 2 3
0 1 3 1
1 1 4 4
0 1 2 2
1 1 2 4
3
-1
*/
分块入门4
题面:
给出一个长为n的数列,以及n个操作,操作涉及区间加法,区间求和。
若\(\mathrm{opt} = 0\),表示将位于 [l, r] 的之间的数字都加 c。
若\(\mathrm{opt} = 1\),表示询问位于 [l, r] 的所有数字的和\(\bmod (c+1)\)。
分析:
将每个块的和放入\(sum\)数组里维护;修改完整的区间只需要对加法标记修改,不完整的则直接修改原数组和\(sum\)数组。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long
using namespace std;
const int N = 1e5 + 5;
ll n, x;
ll a[N], b[N], tag[N], sum[N];
inline void update(ll l, ll r, ll w) {
for (rg int i = l; i <= min(b[l] * x, r); i++) {
a[i] += w;
sum[b[i]] += w;
}
if (b[l] != b[r]) {
for (rg int i = (b[r] - 1) * x + 1; i <= r; i++) {
a[i] += w;
sum[b[i]] += w;
}
}
for (rg int i = b[l] + 1; i <= b[r] - 1; i++) {
tag[i] += w;
}
}
inline ll query(ll l, ll r, ll w) {
rg ll ans = 0;
for (rg int i = l; i <= min(b[l] * x, r); i++) {
ans = (ans + a[i] + tag[b[i]]) % (w + 1);
}
if (b[l] != b[r]) {
for (rg int i = (b[r] - 1) * x + 1; i <= r; i++) {
ans = (ans + a[i] + tag[b[i]]) % (w + 1);
}
}
for (rg int i = b[l] + 1; i <= b[r] - 1; i++) {
ans = (ans + sum[i] + tag[i] * x) % (w + 1);
}
return ans % (w + 1);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
rg ll opt, l, r, w;
cin >> n;
x = sqrt(n);
for (rg int i = 1; i <= n; i++) {
cin >> a[i];
b[i] = (i - 1) / x + 1;
sum[b[i]] += a[i];
}
for (rg int i = 1; i <= n; i++) {
cin >> opt >> l >> r >> w;
if (opt) cout << query(l, r, w) << "\n";
else update(l, r, w);
}
return qwq;
}
/*
4
1 2 2 3
0 1 3 1
1 1 4 4
0 1 2 2
1 1 2 4
1
4
*/
分块入门5
题面:
给出一个长为n的数列,以及n个操作,操作涉及区间开方,区间求和。
若\(opt = 0\),表示将位于 [l, r] 的之间的数字都开方。对于区间中每个 \(a_i(l\le i\le r),\: a_i \leftarrow \left\lfloor \sqrt{a_i}\right\rfloor\)
若\(opt = 1\),表示询问位于 [l, r] 的所有数字的和。
分析:
我们知道\(2^{32}\)最多6次开方就变成了1,所以我们可以记录一个块是否都是\(1/0\),如果是的话那么我们不需要再对其进行开方,因为结果不会变了;否则我们直接遍历对每个元素进行开方。当然,对于非整块我们直接遍历即可。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 5e4 + 5;
int a[N], b[N], L[N], R[N]; //表示第i个块的左、右端点
int n, x, num;
int sum[N], tag[N]; //分别存每个块的和,以及这个块是否只有0或1
inline void update(int l, int r) {
if (tag[b[l]] == 0) {
tag[b[l]] = 1;
for (rg int i = l; i <= min(R[b[l]], r); i++) {
sum[b[i]] -= a[i];
a[i] = sqrt(a[i]);
sum[b[i]] += a[i];
}
for (rg int i = L[b[l]]; i <= R[b[l]]; i++) {
if (a[i] > 1) {
tag[b[l]] = 0;
break;
}
}
}
if (b[l] != b[r] && tag[b[r]] == 0) {
tag[b[r]] = 1;
for (rg int i = L[b[r]]; i <= r; i++) {
sum[b[i]] -= a[i];
a[i] = sqrt(a[i]);
sum[b[r]] += a[i];
}
for (rg int i = L[b[r]]; i <= R[b[r]]; i++) {
if (a[i] > 1) {
tag[b[r]] = 0;
break;
}
}
}
for (rg int i = b[l] + 1; i <= b[r] - 1; i++) {
if (tag[i] == 1) continue;
sum[i] = 0;
tag[i] = 1;
for (rg int j = L[i]; j <= R[i]; j++) {
a[j] = sqrt(a[j]);
sum[i] += a[j];
if (a[j] > 1) tag[i] = 0;
}
}
}
inline int query(int l, int r) {
rg int ans = 0;
for (rg int i = l; i <= min(r, R[b[l]]); i++) {
ans += a[i];
}
if (b[l] != b[r]) {
for (rg int i = L[b[r]]; i <= r; i++) {
ans += a[i];
}
}
for (rg int i = b[l] + 1; i <= b[r] - 1; i++) {
ans += sum[i];
}
return ans;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
x = sqrt(n);
num = n / x;
if (n % x) num++;
for (rg int i = 1; i <= num; i++) {
L[i] = (i - 1) * x + 1;
R[i] = i * x;
}
R[num] = n;
for (rg int i = 1; i <= n; i++) {
cin >> a[i];
b[i] = (i - 1) / x + 1;
sum[b[i]] += a[i];
}
rg int l, r, w, opt;
for (rg int i = 1; i <= n; i++) {
cin >> opt >> l >> r >> w;
if (opt) cout << query(l, r) << "\n";
else update(l, r);
}
return qwq;
}
/*
4
1 2 2 3
0 1 3 1
1 1 4 4
0 1 2 2
1 1 2 4
6
2
*/
分块入门6
题面:
给定一个长为n的数列,以及n个操作,操作涉及单点插入,单点询问。
若\(opt = 0\),表示在第\(l\)个数字前插入数字r(w忽略)。
若\(opt = 1\),表示询问\(a_r\)的值(\(l\)和w忽略)。
分析:
之前提到过,如果我们块内使用数组以外的数据结构,能够支持其它不一样的操作,比如此题块内可以放一个动态的数组,每次插入时先找到位置所在地块,再暴力插入,把块内的其他元素直接向后移动一位,当然用链表也是可以的。
查询的时候类似。
但如果在一个块有大量单点插入,这个块的大小会大大超过\(\sqrt n\),那块内的暴力就没有复杂度保证了。于是还需要引入一个操作:重新分块。
每\(\sqrt n\)次插入后,重新把数列平均分一下块。当然,也可以是某个块过大时重构,或只把这个块分成两半。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 1e5 + 5;
int n, x;
int a[N << 1], b[N];
vector<int> block[350];
inline void insert(int p, int v) {
rg int now_size = 0, whi;
for (rg int i = 1; ; i++) {
rg int size = block[i].size();
now_size += size;
if (now_size >= p) {
whi = i;
p -= (now_size - size);
break;
}
}
block[whi].insert(block[whi].begin() + p - 1, v);
}
inline int query(int p) {
rg int now_size = 0, whi;
for (rg int i = 1; ; i++) {
rg int size = block[i].size();
now_size += size;
if (now_size >= p) {
whi = p - (now_size - size);
return block[i][whi - 1];
}
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
x = sqrt(n);
for (rg int i = 1; i <= n; i++) {
cin >> a[i];
b[i] = (i - 1) / x + 1;
block[b[i]].push_back(a[i]);
}
rg int opt, l, r, w;
for (rg int i = 1; i <= n; i++) {
cin >> opt >> l >> r >> w;
if (opt) cout << query(r) << "\n";
else insert(l, r);
}
return qwq;
}
/*
4
1 2 2 3
0 1 3 1
1 1 4 4
0 1 2 2
1 1 2 4
2
3
*/
分块入门7
题面:
给出一个长为n的数列,以及n个操作,操作涉及区间乘法,区间加法,单点询问。
若\(op = 0\),表示将位于 [l, r] 的之间的数字都加 c。
若\(opt = 1\),表示将位于 [l, r] 的之间的数字都乘 c。
若\(opt = 2\),表示询问\(a_r\)的值\(\bmod 10007\)(\(l\)和\(c\)忽略)。
分析:
先强制乘法比加法优先。
对每个块,用两个标记\(add[i],mul[i]\)分别表示整个块内加和乘的值。
对于一个元素\(a[i]\)实际的值为\(a[i]\times mul[b[i]]+add[b[i]]\)
对于乘法修改操作,标记\(add[i]\)和\(mul[i]\)分别变成\(add[i]\times val\)和\(mul[i]\times val\),对于加法操作,标记\(add[i]\)和\(mul[i]\)分别变成\(add[i]+val\)和\(mul[i]\)。
对于零散元素,直接暴力操作,标记清空即可。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long
using namespace std;
const int mod = 10007;
const int N = 1e5 + 5, M = 350;
ll a[N], add[M], mul[M];
int n, x, b[N];
inline void pushdown(int p) {
for (rg int i = (p - 1) * x + 1; i <= p * x; i++) {
a[i] = (a[i] * mul[p] % mod + add[p]) % mod;
}
add[p] = 0;
mul[p] = 1;
}
inline void update1(int l, int r, ll w) {
pushdown(b[l]);
for (rg int i = l; i <= min(b[l] * x, r); i++) {
a[i] = (a[i] + w) % mod;
}
if (b[l] != b[r]) {
pushdown(b[r]);
for (rg int i = (b[r] - 1) * x + 1; i <= r; i++) {
a[i] = (a[i] + w) % mod;
}
}
for (rg int i = b[l] + 1; i <= b[r] - 1; i++) {
add[i] = (add[i] + w) % mod;
}
}
inline void update2(int l, int r, ll w) {
pushdown(b[l]);
for (rg int i = l; i <= min(b[l] * x, r); i++) {
a[i] = a[i] * w % mod;
}
if (b[l] != b[r]) {
pushdown(b[r]);
for (rg int i = (b[r] - 1) * x + 1; i <= r; i++) {
a[i] = a[i] * w % mod;
}
}
for (rg int i = b[l] + 1; i <= b[r] - 1; i++) {
add[i] = add[i] * w % mod;
mul[i] = mul[i] * w % mod;
}
}
inline ll query(int p) {
return (1ll * a[p] * mul[b[p]] % mod + add[b[p]]) % mod;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
x = sqrt(n);
for (rg int i = 1; i <= n; i++) {
cin >> a[i];
b[i] = (i - 1) / x + 1;
mul[b[i]] = 1;
}
rg int opt, l, r;
rg ll w;
for (rg int i = 1; i <= n; i++) {
cin >> opt >> l >> r >> w;
if (opt == 0) {
update1(l, r, w);
} else if (opt == 1) {
update2(l, r, w);
} else {
cout << query(r) << "\n";
}
}
return qwq;
}
/*
7
1 2 2 3 9 3 2
0 1 3 1
2 1 3 1
1 1 4 4
0 1 7 2
1 2 6 4
1 1 6 5
2 2 6 4
3
100
*/
分块入门8
题面:
区间询问等于c的元素个数,并将这个区间的所有元素改为c。
分析:
这题需要一个\(flag\)数组,用\(flag[i]\)表示第i个块内的元素全部是多少。规定\(flag[i]==-1\)表示这个块里的元素不是同一个元素。
对整块:
若块内元素相同,那么块里元素都是查询元素,则把块的长度加到答案里;若块里元素不同,则暴力查询块内有多少个是c,然后令\(flag[i]=c\)。
对零散块:
若是所在块\(flag \ne -1\),那么要先将标记下传并清空,然后再暴力查询并修改。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long
using namespace std;
const int N = 1e5 + 5, M = 350;
int n, x, num;
ll a[N], L[M], R[M], b[N], flag[M];
inline ll query(ll l, ll r, ll c) {
rg ll ans = 0;
if (flag[b[l]] != -1) {
for (rg int i = L[b[l]]; i <= R[b[l]]; i++) {
a[i] = flag[b[l]];
}
flag[b[l]] = -1;
}
for (rg int i = l; i <= min(R[b[l]], r); i++) {
if (a[i] == c) ans++;
a[i] = c;
}
if (b[l] != b[r]) {
if (flag[b[r]] != -1) {
for (rg int i = L[b[r]]; i <= R[b[r]]; i++) {
a[i] = flag[b[r]];
}
flag[b[r]] = -1;
}
for (rg int i = L[b[r]]; i <= r; i++) {
if (a[i] == c) ans++;
a[i] = c;
}
}
for (rg int i = b[l] + 1; i <= b[r] - 1; i++) {
if (flag[i] != -1) {
if (flag[i] == c) ans += R[i] - L[i] + 1;
} else {
for (rg int j = L[i]; j <= R[i]; j++) {
if (a[j] == c) ans++;
}
}
flag[i] = c;
}
return ans;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
x = sqrt(n);
num = n / x;
if (n % x) num++;
for (rg ll i = 1; i <= n; i++) {
cin >> a[i];
b[i] = (i - 1) / x + 1;
flag[b[i]] = -1;
}
for (rg ll i = 1; i <= num; i++) {
L[i] = (i - 1) * x + 1;
R[i] = x * i;
}
R[num] = n;
rg ll l, r, c;
for (rg int i = 1; i <= n; i++) {
cin >> l >> r >> c;
cout << query(l, r, c) << "\n";
}
return qwq;
}
/*
4
1 2 2 4
1 3 1
1 4 4
1 2 2
1 4 2
1
1
0
2
*/
分块入门9
题面:
给出一个长为n的序列,以及n个操作,操作涉及询问区间的最小众数。
分析:
先离散化数据,每读入一个数\(a[i]\),如果\(a[i]\)没有出现过,那么就用map存它的位置,然后再用val数组存这个位置存的值;如果出现过,那么\(a[i]\)就存map里的值,也就是存下它第一次出现的位置,最后放到vector里面。
通过预处理使\(max[i][j]\)表示块i到块j之间的众数,再二分答案,每次查询时查询边界上的两块的众数和中间块的众数即可。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 1e5 + 5;
int n, x, tot;
int a[N], b[N], val[N], num[N];
bool vis[N];
int maxx[505][505];
map<int, int> mp;
vector<int> v[N];
inline void init(int p) { //预处理maxx[][]
memset(num, 0, sizeof(num));
rg int numm = 0, id = 0;
for (rg int i = (p - 1) * x + 1; i <= n; i++) {
num[a[i]]++;
if (num[a[i]] > numm || (num[a[i]] == numm && val[a[i]] < val[id])) {
numm = num[a[i]];
id = a[i];
}
maxx[p][b[i]] = id;
}
}
inline int dich(int l, int r, int p) { //返回p在i到j中出现的次数
return upper_bound(v[p].begin(), v[p].end(), r) - lower_bound(v[p].begin(), v[p].end(), l);
}
inline int query(int l, int r) {
rg int res = maxx[b[l] + 1][b[r] - 1], numm = dich(l, r, res);
for (rg int i = l; i <= min(b[l] * x, r); i++) {
rg int tmp = dich(l, r, a[i]);
if (tmp > numm || (tmp == numm && val[a[i]] < val[res])) {
numm = tmp;
res = a[i];
}
}
if (b[l] != b[r]) {
for (rg int i = (b[r] - 1) * x + 1; i <= r; i++) {
rg int tmp = dich(l, r, a[i]);
if (tmp > numm || (tmp == numm && val[a[i]] < val[res])) {
numm = tmp;
res = a[i];
}
}
}
return val[res];
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
x = 200;
for (rg int i = 1; i <= n; i++) {
cin >> a[i];
b[i] = (i - 1) / x + 1;
if (mp[a[i]] == 0) {
mp[a[i]] = ++tot;
val[tot] = a[i];
}
a[i] = mp[a[i]]; //存它第一次出现的位置
v[a[i]].push_back(i);
}
for (rg int i = 1; i <= b[n]; i++) init(i);
rg int l, r;
for (rg int i = 1; i <= n; i++) {
cin >> l >> r;
cout << query(l, r) << "\n";
}
return qwq;
}
/*
4
1 2 2 4
1 2
1 4
2 4
3 4
1
2
2
2
*/
例题1:敌兵布阵
题面:
分析:
没什么好说的,单点改,区间查。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long
using namespace std;
const int N = 1e5 + 5;
int n, m, x;
int a[N], b[N], sum[N];
inline void add(int p, int w) {
a[p] += w;
sum[b[p]] += w;
}
inline int query(int l, int r) {
rg int ans = 0;
for (rg int i = l; i <= min(b[l] * x, r); i++) ans += a[i];
if (b[l] != b[r]) {
for (rg int i = (b[r] - 1) * x + 1; i <= r; i++) ans += a[i];
}
for (rg int i = b[l] + 1; i <= b[r] - 1; i++) {
ans += sum[i];
}
return ans;
}
int T;
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> T;
rg int id = 1;
while (T--) {
cout << "Case " << id << ":" << "\n";
id++;
memset(b, 0, sizeof(b));
memset(sum, 0, sizeof(sum));
cin >> n;
x = sqrt(n);
for (rg int i = 1; i <= n; i++) {
cin >> a[i];
b[i] = (i - 1) / x + 1;
sum[b[i]] += a[i];
}
rg string s;
rg int p, w;
while (cin >> s && s != "End") {
cin >> p >> w;
if (s == "Add") {
add(p, w);
} else if (s == "Sub") {
add(p, -w);
} else {
cout << query(p, w) << "\n";
}
}
}
return qwq;
}
例题2:蒲公英
题面:
分析:
和 分块入门9 差不多,求区间众数。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
using namespace std;
const int N = 4e4 + 5;
int n, m, x, tot;
int a[N], b[N], val[N], num[N];
bool vis[N];
int maxx[405][405];
map<int, int> mp;
vector<int> v[N];
inline void init(int p) { //预处理maxx[][]
memset(num, 0, sizeof(num));
rg int numm = 0, id = 0;
for (rg int i = (p - 1) * x + 1; i <= n; i++) {
num[a[i]]++;
if (num[a[i]] > numm || (num[a[i]] == numm && val[a[i]] < val[id])) {
numm = num[a[i]];
id = a[i];
}
maxx[p][b[i]] = id;
}
}
inline int dich(int l, int r, int p) { //返回p在i到j中出现的次数
return upper_bound(v[p].begin(), v[p].end(), r) - lower_bound(v[p].begin(), v[p].end(), l);
}
inline int query(int l, int r) {
rg int res = maxx[b[l] + 1][b[r] - 1], numm = dich(l, r, res);
for (rg int i = l; i <= min(b[l] * x, r); i++) {
rg int tmp = dich(l, r, a[i]);
if (tmp > numm || (tmp == numm && val[a[i]] < val[res])) {
numm = tmp;
res = a[i];
}
}
if (b[l] != b[r]) {
for (rg int i = (b[r] - 1) * x + 1; i <= r; i++) {
rg int tmp = dich(l, r, a[i]);
if (tmp > numm || (tmp == numm && val[a[i]] < val[res])) {
numm = tmp;
res = a[i];
}
}
}
return val[res];
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
x = 100;
for (rg int i = 1; i <= n; i++) {
cin >> a[i];
b[i] = (i - 1) / x + 1;
if (mp[a[i]] == 0) {
mp[a[i]] = ++tot;
val[tot] = a[i];
}
a[i] = mp[a[i]]; //存它第一次出现的位置
v[a[i]].push_back(i);
}
for (rg int i = 1; i <= b[n]; i++) init(i);
rg int l, r, last = 0;
for (rg int i = 1; i <= m; i++) {
cin >> l >> r;
l = (l + last - 1) % n + 1;
r = (r + last - 1) % n + 1;
if (l > r) swap(l, r);
last = query(l, r);
cout << last << "\n";
}
return qwq;
}
例题3:弹飞绵羊
题面:
分析:
每个点记录跳出分块的步数以及跳到下一分块的哪个点。
在进行更新的时候只需对更新位置所在的分块进行更新就可以了。
#include<bits/stdc++.h>
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 2e5 + 5, M = 600;
int n, m, x;
int a[N], b[N];
int st[N], pt[N]; //st[i]记录从i跳几步跳出当前块,pt[i]记录跳出当前块后到哪个块
inline void update(int p) {
rg int w;
cin >> w;
a[p] = w;
for (rg int i = p; i >= (b[p] - 1) * x + 1; i--) {
if (b[i] == b[i + a[i]]) {
st[i] = st[i + a[i]] + 1;
pt[i] = pt[i + a[i]];
} else {
st[i] = 1;
pt[i] = i + a[i];
}
}
}
inline int query(int p) {
rg int tmp = 0;
while (p <= n) {
tmp += st[p];
p = pt[p];
}
return tmp;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
x = sqrt(n);
for (rg int i = 1; i <= n; i++) {
cin >> a[i];
b[i] = (i - 1) / x + 1;
}
for (rg int i = n; i > 0; i--) {
if (b[i] == b[i + a[i]]) {
st[i] = st[i + a[i]] + 1;
pt[i] = pt[i + a[i]];
} else {
st[i] = 1;
pt[i] = i + a[i];
}
}
cin >> m;
rg int u, v;
for (rg int i = 1; i <= m; i++) {
cin >> u >> v;
v++;
if (u == 1) {
cout << query(v) << "\n";
} else {
update(v);
}
}
return qwq;
}
例题4:教主的魔法
题面:
分析:
类似于 分块入门2。
#include<bits/stdc++.h>
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 1e6 + 3;
int n, q, x;
int a[N], b[N], tag[N];
vector<int> v[1003];
inline void resort(int o) {
v[o].clear();
for (rg int i = (o - 1) * x + 1; i <= min(o * x, n); i++) {
v[o].push_back(a[i]);
}
sort(v[o].begin(), v[o].end());
}
inline void add(int l, int r, int w) {
for (rg int i = l; i <= min(b[l] * x, r); i++) {
a[i] += w;
}
resort(b[l]);
if (b[l] != b[r]) {
for (rg int i = (b[r] - 1) * x + 1; i <= r; i++) {
a[i] += w;
}
resort(b[r]);
}
for (rg int i = b[l] + 1; i <= b[r] - 1; i++) {
tag[i] += w;
}
}
inline int query(int l, int r, int w) {
rg int ans = 0;
for (rg int i = l; i <= min(b[l] * x, r); i++) {
if (a[i] + tag[b[l]] >= w) ans++;
}
if (b[l] != b[r]) {
for (rg int i = (b[r] - 1) * x + 1; i <= r; i++) {
if (a[i] + tag[b[r]] >= w) ans++;
}
}
for (rg int i = b[l] + 1; i <= b[r] - 1; i++) {
rg int x = w - tag[i];
ans += v[i].size() - (lower_bound(v[i].begin(), v[i].end(), x) - v[i].begin());
}
return ans;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
char c;
int l, r, w;
cin >> n >> q;
x = sqrt(n);
for (rg int i = 1; i <= n; i++) {
cin >> a[i];
b[i] = (i - 1) / x + 1;
v[b[i]].push_back(a[i]);
}
for (rg int i = 1; i <= b[n]; i++) sort(v[i].begin(), v[i].end());
for (rg int i = 1; i <= q; i++) {
cin >> c >> l >> r >> w;
if (c == 'M') {
add(l, r, w);
} else {
cout << query(l, r, w) << "\n";
}
}
return qwq;
}
例题5:数颜色
题面:
分析:
很怪。
洛谷上数据加强了,分块好像被卡掉了,于是用oj上的数据范围作例题,洛谷上的等下面莫队再写吧。虽然原来那个数据范围暴力就能过……
设\(last[i]\)表示上一个颜色为\(a[i]\)的点。
对每块进行排序,存入\(pre\)数组。
- 如果是修改的话,重新做一遍\(last[]\)和\(pre[]\)
- 如果是查找答案的话,左半边和右半边暴力找\(last[i]<l\)的,整块在\(pre[]\)中用二分来算。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 10003, M = 1000003;
int n, m, x;
int a[N], b[N], L[N], R[N], last[M], pre[N], bf[N];
inline void reset(int o) {
for (rg int i = L[o]; i <= R[o]; i++) {
pre[i] = bf[i];
}
sort(pre + L[o], pre + R[o] + 1);
}
inline void update(int o, int val) {
for (rg int i = 1; i <= n; i++) last[a[i]] = 0;
a[o] = val;
for (rg int i = 1, tmp; i <= n; i++) {
tmp = bf[i];
bf[i] = last[a[i]];
if (bf[i] != tmp) reset(b[i]);
last[a[i]] = i;
}
}
inline int query(int l, int r) {
rg int ans = 0;
for (rg int i = l; i <= R[b[l]]; i++) {
if (bf[i] < l) ans++;
}
if (b[l] != b[r]) {
for (rg int i = L[b[r]]; i <= r; i++) {
if (bf[i] < l) ans++;
}
}
for (rg int i = b[l] + 1; i <= b[r] - 1; i++) {
ans += lower_bound(pre + L[i], pre + R[i] + 1, l) - pre - L[i];
}
return ans;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
x = sqrt(n);
for (rg int i = 1; i <= n; i++) {
cin >> a[i];
b[i] = (i - 1) / x + 1;
bf[i] = last[a[i]];
last[a[i]] = i;
}
for (rg int i = 1; i <= b[n]; i++) {
L[i] = (i - 1) * x + 1;
R[i] = i * x;
}
R[b[n]] = n;
for (rg int i = 1; i <= b[n]; i++) reset(i);
rg char ch;
int l, r;
for (rg int i = 1; i <= m; i++) {
cin >> ch >> l >> r;
if (ch == 'Q') cout << query(l, r) << "\n";
else update(l, r);
}
return qwq;
}
例题6:颜色
题面:
分析:
预处理\(cnt[i][k]\)表示前i块中有多少个位置颜色为j,\(sum[i][j][k]\)表示第i块到第j块中颜色 [1,k] 的贡献。
对于和的平方,我们这样处理:
比如对于3的平方,可以拆为\(3^2 = 1 + 3 + 5 = (0\times2+1) + (1\times2+1) + (2\times2+1) = 9\)
可以找到规律:
对于数字x,它的平方表示为:\(\displaystyle\sum_{i=0}^{x-1}i\times2+1\)。
而如果我们已经知道了\(0\sim k\)的贡献,我们从\(k+1\)开始继续进行上面的操作即可。
对于查询:
先加上中间整块的贡献,然后将整块内所有颜色已经出现的次数统计起来,之后枚举左右半块中的数,每碰到一个数我们就进行一次\(\times2+1\)的操作,最终得到的就是总贡献。
特别要注意,若是查询的左右区间在同一块中,统计整块内颜色出现的次数时要和\(0\)取\(max\)。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long
using namespace std;
const int N = 5e4 + 5, M = 52;
int n, m, q, x;
int a[N], b[N], L[M], R[M], t[N], cnt[M][20005];
ll sum[M][M][20005];
inline ll query(int l, int r, int aa, int bb) {
rg ll ans = sum[b[l] + 1][b[r] - 1][bb] - sum[b[l] + 1][b[r] - 1][aa - 1];
for (rg int i = l; i <= min(R[b[l]], r); i++) {
if (a[i] < aa || a[i] > bb) continue;
//注意和0取max!!!
if (!t[a[i]]) t[a[i]] = max(0, cnt[b[r] - 1][a[i]] - cnt[b[l]][a[i]]);
ans += t[a[i]] * 2 + 1;
t[a[i]]++;
}
if (b[l] != b[r]) {
for (rg int i = L[b[r]]; i <= r; i++) {
if (a[i] < aa || a[i] > bb) continue;
if (!t[a[i]]) t[a[i]] = cnt[b[r] - 1][a[i]] - cnt[b[l]][a[i]];
ans += t[a[i]] * 2 + 1;
t[a[i]]++;
}
}
for (rg int i = l; i <= min(R[b[l]], r); i++) t[a[i]] = 0;
for (rg int i = L[b[r]]; i <= r; i++) t[a[i]] = 0;
return ans;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m >> q;
x = (int)pow(n, 2.0 / 3);
for (rg int i = 1; i <= n; i++) {
cin >> a[i];
b[i] = (i - 1) / x + 1;
}
for (rg int i = 1; i <= b[n]; i++) {
L[i] = (i - 1) * x + 1;
R[i] = i * x;
}
R[b[n]] = n;
for (rg int i = 1; i <= b[n]; i++) {
for (rg int j = 1; j <= m; j++) {
cnt[i][j] = cnt[i - 1][j];
}
for (rg int j = L[i]; j <= R[i]; j++) {
cnt[i][a[j]]++;
}
}
for (rg int i = 1; i <= b[n]; i++) {
for (rg int j = i; j <= b[n]; j++) {
for (rg int k = 1; k <= m; k++) {
sum[i][j][k] = sum[i][j - 1][k];
}
for (rg int k = L[j]; k <= R[j]; k++) {
sum[i][j][a[k]] += t[a[k]] * 2 + 1;
t[a[k]]++;
}
}
for (rg int j = L[i]; j <= n; j++) t[a[j]] = 0;
}
for (rg int i = 1; i <= b[n]; i++) {
for (rg int j = i; j <= b[n]; j++) {
for (rg int k = 1; k <= m; k++) {
sum[i][j][k] += sum[i][j][k - 1];
}
}
}
rg ll ans = 0;
rg int l, r, aa, bb;
for (rg int i = 1; i <= q; i++) {
cin >> l >> r >> aa >> bb;
l = (l ^ ans);
r = (r ^ ans);
aa = (aa ^ ans);
bb = (bb ^ ans);
ans = query(l, r, aa, bb);
cout << ans << "\n";
}
return qwq;
}
二、莫队
用处与思想
适用题型:
(1)区间询问问题,且区间信息不可高效合并,即传统数据结构难以维护。
(2)必须可以离线。
(3)不带修改(或简单修改)
(4)若已知区间\([L1,R1]\)的答案,我们可以花费\(O(|L1-L2|)\)的时间将左端点移到\(L2\),花费\(O(|R1-R2|)\)的时间将右端点移到\(R2\)的位置,从而得到区间\([L2,R2]\)的答案,即我们区间左右端点移动1的复杂度是\(O(1)\)的。
基本思想:
在我们可以\(O(1)\)地移动区间左右端点的前提下,莫队就是将所有的询问区间按照一定顺序排好,然后从第一个区间开始进行区间的移动,每次移动完一个区间就进行答案的统计,每一个区间的答案从上一个移动好的区间移动过去,而非从头开始移动,我们一开始认为已知\([0,0]\)的答案。
对于莫队的大小:
普通莫队:\(\sqrt n\);带修莫队:\(n^{\frac23}\)
1.普通莫队
莫队是莫涛归纳总结的一种解决区间查询等问题的离线算法,基于分块思想,复杂度为\(O(n\times \sqrt n)\)。
应用环境对于序列上的区间询问问题(序列长度为n,询问为m),如果可以在\(O(1)\)内从\([l,r]\)的答案扩展到与其相邻的答案,可以考虑使用莫队算法来解决问题。
例题1:
题面:
有一个长为n的序列,有m次询问,每次询问某个区间内出现过的数值种类数。
分析:
令\(tmp[i]\)表示i出现的次数,在移动区间的过程中对这个数组进行操作:若\(tmp[i]\)在加入了一次i之后为1则为出现了一个新数,同理若\(tmp[i]\)在删去了一个i之后为0则消失了一个数。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 5e4 + 5, M = 2e5 + 5, V = 1e6 + 5;
struct node {
int l, r, pos, id;
} q[M];
int a[N], b[N], ans[M], tmp[V], n, x, m, res;
inline bool cmp(node l, node r) {
if (b[l.l] != b[r.l]) return b[l.l] < b[r.l];
return l.r < r.r;
}
inline void add(int val) { if ((++tmp[val]) == 1) res++; }
inline void del(int val) { if ((--tmp[val]) == 0) res--; }
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
x = sqrt(n);
for (rg int i = 1; i <= n; i++) {
cin >> a[i];
b[i] = (i - 1) / x + 1;
}
//system("pauss");
for (rg int i = 1; i <= m; i++) {
cin >> q[i].l >> q[i].r;
q[i].pos = i;
}
sort(q + 1, q + m + 1, cmp);
rg int now_l = 0, now_r = 0;
for (rg int i = 1; i <= m; i++) {
while (now_l > q[i].l) add(a[--now_l]); //这个数加过了,所以加减过后的
while (now_r < q[i].r) add(a[++now_r]);
while (now_l < q[i].l) del(a[now_l++]); //这个数也要删,所以先删再加
while (now_r > q[i].r) del(a[now_r--]);
ans[q[i].pos] = res;
}
for (rg int i = 1; i <= m; i++) {
cout << ans[i] << "\n";
}
return qwq;
}
普通莫队的优化
我们看一下下面这几组询问(设块的大小为2)
1 1
2 100
3 3
4 100
手动模拟一下可以发现,r指针的移动次数大概为300次,我们处理完第一个块后,\(l=2,r=100\),此时只需要移动两次\(l\)指针就可以得到第四个询问的答案,但我们却要将r指针移动到3来获取第三个询问的答案,再移动到100获取第四个询问的答案,这样多了九十几次的指针移动。我们怎么优化这个地方呢? 我们就要用到奇偶化排序。
奇偶化排序即对于属于奇数块的询问,r按照从小到大排序,对于偶数块的排序,r从大到小排序,这样我们的r指针在处理完这个奇数块的问题后,将在返回的途中处理偶数块的问题,再向n移动处理下一个奇数块的问题,优化了r指针的移动次数。一般情况下,这种优化能让程序快\(30\%\)左右。
inline bool cmp(node l, node r) {
if (b[l.l] != b[r.l]) return l.l < r.l;
if (b[l.l] & 1) return l.r < r.r;
return l.r > r.r;
}
例题2:小Z的袜子
题面:
分析:
对于区间\([i,i]\),由于只有一个元素,我们很容易就能知道答案。然后一步一步从当前区间向下一个区间靠近。
我们设\(col[i]\)表示当前颜色i出现了多少次,ans表示当前共有多少种可行的配对方案,然后每次移动的时候更新答案——设当前颜色为k,如果是增长区间就是ans加上\(C_{col[k]+1}^{2}-C_{col[k]}^{2}\),如果是缩短区间就是ans减去\(C_{col[k]}^{2}-C_{col[k]-1}^{2}\)。
而这个询问的答案就是\(\frac{ans}{C_{r-l+1}^{2}}\)。
这里有个优化:
\(C_{a}^{2}=\frac{a(a-1)}{2}\),
所以\(C_{a+1}^{2}-C_{a}^{2}=\frac{(a+1)a}{2}-\frac{a(a-1)}{2}=\frac{a}{2}\times(a+1-a-1)=\frac{a}{2}\times 2=a\),
所以\(C_{col[k]+1}^{2}-C_{col[k]
}^{2}=col[k]\)。
注意:因为\(now\_l\)初始在0,所以要把\(col[a[0]]\)设为1来当作查过这一位,不然在\(now\_l\)右移到1时会让\(res-(-1)\)使结果错误。当然,令\(now\_l\)初始在1也可以避免这个问题。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
using namespace std;
const int N = 5e4 + 5;
struct node {
int l, r, pos;
} q[N];
int a[N], b[N], ans[N], col[N], n, m, x, res;
int ql[N], qr[N];
inline bool cmp(node l, node r) {
if (b[l.l] != b[r.l]) return b[l.l] < b[r.l];
if (b[l.l] & 1) return l.r < r.r;
return l.r > r.r;
}
inline void add(int val) {
res += col[a[val]];
col[a[val]]++;
}
inline void del(int val) {
col[a[val]]--;
res -= col[a[val]];
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
x = sqrt(n);
for (rg int i = 1; i <= n; i++) {
cin >> a[i];
b[i] = (i - 1) / x + 1;
}
for (rg int i = 1; i <= m; i++) {
cin >> q[i].l >> q[i].r;
ql[i] = q[i].l;
qr[i] = q[i].r;
q[i].pos = i;
}
sort(q + 1, q + m + 1, cmp);
rg int now_l = 0, now_r = 0;
col[a[0]]++;
for (rg int i = 1; i <= m; i++) {
while (now_l < q[i].l) del(now_l++);
while (now_r > q[i].r) del(now_r--);
while (now_l > q[i].l) add(--now_l);
while (now_r < q[i].r) add(++now_r);
ans[q[i].pos] = res;
}
for (rg int i = 1; i <= m; i++) {
if (ql[i] == qr[i]) {
cout << "0/1\n";
continue;
}
rg int fm = (qr[i] - ql[i]) * (qr[i] - ql[i] + 1) / 2;
rg int y = __gcd(fm, ans[i]);
cout << ans[i] / y << "/" << fm / y << "\n";
}
return qwq;
}
例题3:小B的询问
题面
分析:
对于每次移动,设当前这位数是k,先减去\(col[k]^2\),再将\(col[k]\)加/减,再加上\(col[k]^2\)即可完成转移。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
using namespace std;
const int N = 5e4 + 5;
struct node {
int l, r, pos;
} q[N];
int a[N], b[N], ans[N], col[N], n, m, k, x, res;
int ql[N], qr[N];
inline bool cmp(node l, node r) {
if (b[l.l] != b[r.l]) return b[l.l] < b[r.l];
if (b[l.l] & 1) return l.r < r.r;
return l.r > r.r;
}
inline void add(int val) {
res -= col[a[val]] * col[a[val]];
col[a[val]]++;
res += col[a[val]] * col[a[val]];
}
inline void del(int val) {
res -= col[a[val]] * col[a[val]];
col[a[val]]--;
res += col[a[val]] * col[a[val]];
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m >> k;
x = sqrt(n);
for (rg int i = 1; i <= n; i++) {
cin >> a[i];
b[i] = (i - 1) / x + 1;
}
for (rg int i = 1; i <= m; i++) {
cin >> q[i].l >> q[i].r;
q[i].pos = i;
}
sort(q + 1, q + m + 1, cmp);
rg int now_l = 1, now_r = 0;
for (rg int i = 1; i <= m; i++) {
while (now_l < q[i].l) del(now_l++);
while (now_r > q[i].r) del(now_r--);
while (now_l > q[i].l) add(--now_l);
while (now_r < q[i].r) add(++now_r);
ans[q[i].pos] = res;
}
for (rg int i = 1; i <= m; i++) {
cout << ans[i] << "\n";
}
return qwq;
}
例题4:作业
题面:
分析:
将莫队和分块结合起来,对于询问区间间的转移用莫队维护,对ans的更新用分块维护。
oj上很sb的是它的数据范围实际是\(10^6\)但题目写的是\(10^5\)。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 1e6 + 3;
int n, m, size, cnt;
int a[N], b[N], ans1[N], ans2[N];
int tmp[N], num[N], tot[N]; //分别表示 i的个数,整块中的个数,整块中的种类数
struct node {
int l, r, a, b, id;
} q[N];
inline bool cmp(node n1, node n2) {
if (b[n1.l] != b[n2.l]) return b[n1.l] < b[n2.l];
if (b[n1.l] & 1) return n1.r > n2.r;
return n1.r < n2.r;
}
inline void add(int x) {
if (++tmp[a[x]] == 1) tot[b[a[x]]]++;
num[b[a[x]]]++;
}
inline void del(int x) {
if (--tmp[a[x]] == 0) tot[b[a[x]]]--;
num[b[a[x]]]--;
}
inline void get_ans(int aa, int bb, int k) {
for (rg int i = aa; i <= min(bb, b[aa] * size); i++) {
if (tmp[i]) {
ans1[k] += tmp[i];
ans2[k]++;
}
}
if (b[aa] != b[bb]) {
for (rg int i = (b[bb] - 1) * size + 1; i <= bb; i++) {
if (tmp[i]) {
ans1[k] += tmp[i];
ans2[k]++;
}
}
}
for (rg int i = b[aa] + 1; i <= b[bb] - 1; i++) {
ans1[k] += num[i];
ans2[k] += tot[i];
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
size = sqrt(n);
for (rg int i = 1; i <= n; i++) {
cin >> a[i];
b[i] = (i - 1) / size + 1;
}
for (rg int i = 1; i <= m; i++) {
cin >> q[i].l >> q[i].r >> q[i].a >> q[i].b;
q[i].id = i;
}
sort(q + 1, q + m + 1, cmp);
rg int now_l = 1, now_r = 0;
for (rg int i = 1; i <= m; i++) {
while (q[i].l < now_l) add(--now_l);
while (q[i].r > now_r) add(++now_r);
while (q[i].l > now_l) del(now_l++);
while (q[i].r < now_r) del(now_r--);
get_ans(q[i].a, q[i].b, q[i].id);
}
for (rg int i = 1; i <= m; i++) {
cout << ans1[i] << " " << ans2[i] << "\n";
}
return qwq;
}
2.带修莫队
带修莫队与普通莫队基本是一致的,只是会多维护一个值:时间戳。说白了就是这个询问在第几次修改之后。那么我们在进行区间移动的时候,只需要在移动完区间后,再移动一下时间戳,使得时间戳也符合当前询问的条件就好了。
例题5:数颜色
题面:
分析:
令\(tmp[i]\)表示i出现的次数,在移动区间时移动时间戳。
关于\(change\)函数最后的\(swap\)操作的说明:我们在移动时间戳的时候第一次处理这个修改即会将a中对应的值改为c中对应的值,而当我们第二次要处理这个修改就是相当于我们改回去了,所以对于第二次就是将a中对应的值改回去,也就是改成交换后c里的值,交换后再次修改就可以实现这个功能。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 1e6 + 3;
struct node1 {
int l, r, time, id;
} q[N];
struct node2 {
int pos, val;
} c[N];
int tmp[N], a[N], b[N], ans[N], n, m, cnt, tim, x, res;
inline bool cmp(node1 n1, node1 n2) {
if (b[n1.l] != b[n2.l]) return b[n1.l] < b[n2.l];
if (b[n1.r] != b[n2.r]) return b[n1.r] < b[n2.r];
return n1.time < n2.time;
}
inline void add(int val) {
if ((++tmp[a[val]]) == 1) res++;
}
inline void del(int val) {
if ((--tmp[a[val]]) == 0) res--;
}
inline void change(int now_time, int i) {
if (c[now_time].pos >= q[i].l && c[now_time].pos <= q[i].r) { //如果这个改多了的点在区间内
if ((++tmp[c[now_time].val]) == 1) { //如果第now_time个修改的点改成的值的出现种类数是0,那么种类res++
//这个if是对于 while (q[i].time > now_time) change(++now_time, i);来写的
res++;
}
if ((--tmp[a[c[now_time].pos]]) == 0) { //如果第now_time个修改的位置对应原来数列的数在区间出现过1次,那么还原回来肯定要种类res--
//这个if是对于 while (q[i].time < now_time) change(now_time--, i);来写的
res--;
}
}
swap(c[now_time].val, a[c[now_time].pos]); //第now_time次修改为的值和第now_time次修改的值的位置对应原数列的值交换,就达到了“改多了,改回去;改少了,改过来”
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
x = n / sqrt(m);
for (rg int i = 1; i <= n; i++) {
cin >> a[i];
b[i] = (i - 1) / x + 1;
}
rg char ch;
rg int l, r;
for (rg int i = 1; i <= m; i++) {
cin >> ch >> l >> r;
if (ch == 'Q') {
q[++cnt].l = l;
q[cnt].r = r;
q[cnt].time = tim; //tim为时间戳,表示修改了多少次
q[cnt].id = cnt;
} else {
c[++tim].pos = l;
c[tim].val = r;
}
}
sort(q + 1, q + cnt + 1, cmp);
rg int now_time = 0, now_l = 1, now_r = 0;
for (rg int i = 1; i <= cnt; i++) {
while (q[i].l < now_l) add(--now_l);
while (q[i].r > now_r) add(++now_r);
while (q[i].l > now_l) del(now_l++);
while (q[i].r < now_r) del(now_r--);
while (q[i].time < now_time) change(now_time--, i); //改多了,改回去,所以now_time也要该回去
while (q[i].time > now_time) change(++now_time, i); //改少了,改过来,now_time已经改过了,所以不用了
ans[q[i].id] = res;
}
for (rg int i = 1; i <= cnt; i++) {
cout << ans[i] << "\n";
}
return qwq;
}
3.树上莫队
我们知道莫队是基于分块的算法,所以我们需要找到一种树上的分块方法来保证时间复杂度。
条件:
- 属于同一块的节点之间的距离不超过给定块的大小
- 每个块中的节点不能太多也不能太少
- 每个节点都要属于一个块
- 编号相邻的块之间的距离不能太大
例题6:Count on a tree II
题面:
分析:
我们知道这题如果出现在序列上就是普通莫队的裸题,而这题就是树上莫队的裸题。
我们知道要使用莫队算法,必须要将一条路径化为一个区间。从这个意义上来说,树上莫队的思想和树链剖分类似,都是将一棵树化为一个序列,但是树链剖分是将一条路径和若干个序列上的区间对应,而树上莫队算法需要将一条路径和一个序列上的区间对应。
树上莫队的转化方法是这样的:DFS整棵树,在每个点入栈和出栈时,都将这个点的编号记下,按这样的顺序组成一个长为2N的序列(即欧拉序)。
令点i入栈和出栈的时刻为\(in[i]\)和\(out[i]\),对于一条路径\((a,b)\),有以下几种情况:
- (1)a是b的祖先,那么这条路径和序列上的区间\([in[a],in[b]]\)对应。
- (2)b是a的祖先,那么这条路径和序列上的区间\([in[b],in[a]]\)对应。
- (3)a和b无祖孙关系,那么这两条路径和序列上的区间\([out[a],in[b]]\)(或\([out[b],in[a]]\),因为我们不知道a,b的先后顺序)加上\(lca(a,b)\)这个点对应。
有时一个点在区间内出现两次,这种情况下我们不应该计算这个点,因为它表示这个点入栈又出栈了。上面第一、二种情况还好理解,第三种情况就让人有点头痛,一个·区间加一个点是什么操作?实际上,由于\(lca(a,b)\)一定早于点a,b入栈,又一定晚于点a,b出栈,所以上面的区间并没有包含\(lca(a,b)\),计算信息时要加上这个点。同时上述的区间定义可以证明被满足每个要算入答案的点都出现一次且仅一次。
做完上述事情,就是一个裸的莫队算法了。
注意点权是在\([0,2^{31}-1]\)的范围,需要离散化。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 4e4 + 3, M = 8e4 + 3;
int n, m, tim, size;
int in[N], out[N], a[N], p[M], b[M];
int dep[N], ans[100003], fa[N][21];
int cnt[N], sum;
bool cntp[N];
vector<int> e[100003];
struct node {
int val, id;
} f[N];
struct node2 {
int id, l, r, extra;
} q[100003];
inline bool cmpf(node n1, node n2) {
return n1.val < n2.val;
}
inline bool cmpq(node2 n1, node2 n2) {
if (b[n1.l] != b[n2.l]) return b[n1.l] < b[n2.l];
return n1.r < n2.r;
}
inline void dfs(int u) { //求出欧拉序、深度以及p[tim](第tim个询问的点对应原序列编号为u)
in[u] = ++tim;
p[tim] = u;
for (rg int i = 0; i < e[u].size(); i++) {
rg int v = e[u][i];
if (v != fa[u][0]) {
fa[v][0] = u;
dep[v] = dep[u] + 1;
dfs(v);
}
}
out[u] = ++tim;
p[tim] = u;
}
inline int lca(int x, int y) {
if (dep[x] < dep[y]) swap(x, y);
for (rg int i = 20; i >= 0; i--) {
if (dep[fa[x][i]] >= dep[y]) x = fa[x][i];
}
if (x == y) return x;
for (rg int i = 20; i >= 0; i--) {
if (fa[x][i] != fa[y][i]) {
x = fa[x][i];
y = fa[y][i];
}
}
return fa[x][0];
}
inline void expand(int x) {
//p[x]:在欧拉序中编号为x的点在原始树上的节点编号
//cntp[p[x]]:标记p[x]是否在序列里出现过,如果在区间出现过两次,是不算贡献的,那就if加一次,else减一次
cntp[p[x]] = !cntp[p[x]];
if (cntp[p[x]]) {
cnt[a[p[x]]]++; //a[p[x]]:p[x]这个点的值;cnt[a[p[x]]]++表示这个值出现过的次数
if (cnt[a[p[x]]] == 1) sum++; //sum存不同颜色的个数
} else {
cnt[a[p[x]]]--;
if (cnt[a[p[x]]] == 0) sum--;
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
for (rg int i = 1; i <= n; i++) {
f[i].id = i;
cin >> f[i].val;
}
sort(f + 1, f + n + 1, cmpf);
rg int totf = 0;
for (rg int i = 1; i <= n; i++) { //离散化
if (i == 1 || f[i].val != f[i - 1].val) totf++;
a[f[i].id] = totf;
}
for (rg int i = 1; i < n; i++) {
rg int a, b;
cin >> a >> b;
e[a].push_back(b);
e[b].push_back(a);
}
dep[1] = 1;
dfs(1);
for (rg int i = 1; i <= 20; i++) { //预处理倍增
for (rg int j = 1; j <= n; j++) {
fa[j][i] = fa[fa[j][i - 1]][i - 1];
}
}
size = sqrt(n << 1);
for (rg int i = 1; i <= (n << 1); i++) {
b[i] = (i - 1) / size + 1;
}
for (rg int i = 1; i <= m; i++) {
rg int a, b, g;
q[i].id = i;
cin >> a >> b;
g = lca(a, b);
if (g == a || g == b) {
q[i].l = in[a];
q[i].r = in[b];
q[i].extra = 0;
} else {
q[i].extra = g;
if (out[a] <= in[b]) {
q[i].l = out[a];
q[i].r = in[b];
} else {
q[i].l = out[b];
q[i].r = in[a];
}
}
if (q[i].l > q[i].r) swap(q[i].l, q[i].r);
}
sort(q + 1, q + m + 1, cmpq);
rg int now_l = 1, now_r = 0;
for (rg int i = 1; i <= m; i++) {
while (q[i].l < now_l) expand(--now_l);
while (q[i].r > now_r) expand(++now_r);
while (q[i].l > now_l) expand(now_l++);
while (q[i].r < now_r) expand(now_r--);
//处理如果lca不是a和b,把lca加到最后,处理加进来的lca的;
//q[i].extra:如果第i个询问的extra>0,证明lca不是a,b;
//cnt[a[q[i].extra]]:第i个询问的extra所对应的原树编号
//!cnt[a[q[i].extra]]:如果没出现过,那么ans+1,就是把lca加进去
if (q[i].extra && !cnt[a[q[i].extra]]) ans[q[i].id] = sum + 1;
else ans[q[i].id] = sum;
}
for (rg int i = 1; i <= m; i++) {
cout << ans[i] << "\n";
}
return qwq;
}
例题7:王室联邦(树上分块)
题面:
分析:
令B为希望块的大小,首先,对于整个树DFS,当子树的大小大于B时,就将它们分在一块。容易想到:对于根,可能会剩下一些点,于是将这些点分在最后一个块里。
具体地:
(1)我们DFS整棵树,处理每个节点时,将其一部分子节点分块,将未被分块的子节点返回到上一层。
(2)枚举u的每个子节点v,递归处理子树后,将每个子节点返回的未被分块的节点添加到集合S中,一旦\(|S|\ge B\)就把S作为一个新的块并将u作为省会,然后清空S并继续枚举v。
(3)处理完所有子树后,将u也加入到集合S中,此时在S中的节点为未被分块的节点,将其返回到上一层,显然S的大小最大为\(B-1\)个子树节点+u节点本身,即\(|S|\le B\)。
(4)由于返回的集合的大小最大为B,对于一个子树会对集合最多增加\(B-1\)个节点,那么每个块的大小最大为\(2B-1\),满足条件。
(5)在DFS结束后,集合S中可能还有节点(最多有B个),那么我们把这B个节点并入最后一个块(以根节点为省会的最后一个块)中,那么这个块的大小最大为\(3B-1\),符合条件。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 1e3 + 3, M = 2e3 + 3;
int n, B, sz, cnt, tot; //cnt存块的个数
int head[N], to[M], nxt[M], st[N], rt[N], bel[N]; //st为集合S,rt存省会,bel存属于哪个块
inline void add(int u, int v) {
to[++tot] = v;
nxt[tot] = head[u];
head[u] = tot;
}
inline void dfs(int u, int fath) {
rg int cnr = sz;
for (rg int i = head[u]; i; i = nxt[i]) {
rg int v = to[i];
if (v == fath) continue;
dfs(v, u);
if (sz - cnr >= B) {
rt[++cnt] = u;
while (sz > cnr) bel[st[sz--]] = cnt;
}
}
st[++sz] = u;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> B;
for (rg int i = 1; i < n; i++) {
rg int u, v;
cin >> u >> v;
add(u, v);
add(v, u);
}
dfs(1, 0);
if (!cnt) rt[++cnt] = 1;
while (sz) bel[st[sz--]] = cnt;
cout << cnt << "\n";
for (rg int i = 1; i <= n; i++) {
cout << bel[i] << " ";
}
cout << "\n";
for (rg int i = 1; i <= cnt; i++) {
cout << rt[i] << " ";
}
cout << "\n";
return qwq;
}
例题8:bzoj3757 苹果树
题面:
有n个数和m个询问,每次询问输入\(u,v,a,b\)表示查询路径\(u,v\)上的路径,并且将颜色a看作颜色b,输出颜色数。
分析:
如果a和b都出现了并且\(a\ne b\),那么答案-1。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 1e5 + 3;
int n, m, size, a[N], b[N];
vector<int> e[N];
int tim, res, ans[N], in[N], out[N], order[N << 1];
int dep[N], fa[N][21], cnt[N];
bool vis[N];
struct node {
int id, l, r, a, b, extra;
} q[N];
inline bool cmp(node x, node y) {
if (b[x.l] != b[y.l]) return b[x.l] < b[y.l];
return x.r < y.r;
}
inline void dfs(int u) {
in[u] = ++tim;
order[tim] = u;
for (rg int i = 0; i < e[u].size(); i++) {
rg int v = e[u][i];
if (v != fa[u][0]) {
fa[v][0] = u;
dep[v] = dep[u] + 1;
dfs(v);
}
}
out[u] = ++tim;
order[tim] = u;
}
inline int LCA(int x, int y) {
if (dep[x] < dep[y]) swap(x, y);
for (rg int i = 20; i >= 0; i--) {
if (dep[fa[x][i]] >= dep[y]) x = fa[x][i];
}
if (x == y) return x;
for (rg int i = 20; i >= 0; i--) {
if (fa[x][i] != fa[y][i]) {
x = fa[x][i];
y = fa[y][i];
}
}
return fa[x][0];
}
inline void update(int x) {
//对于在序列中出现两次的数,不应计算,则可以加一次再减一次抵消掉
vis[order[x]] = !vis[order[x]];
if (vis[order[x]]) {
cnt[a[order[x]]]++;
if (cnt[a[order[x]]] == 1) res++;
} else {
cnt[a[order[x]]]--;
if (cnt[a[order[x]]] == 0) res--;
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
size = sqrt(n);
rg int root = 0;
for (rg int i = 1; i <= n; i++) {
cin >> a[i];
b[i] = (i - 1) / size + 1;
}
for (rg int i = 1; i <= n; i++) {
rg int u, v;
cin >> u >> v;
if (!u || ! v) {
root = u | v;
} else {
e[u].push_back(v);
e[v].push_back(u);
}
}
dep[root] = 1;
dfs(root);
for (rg int i = 1; i <= 20; i++) {
for (rg int j = 1; j <= n; j++) {
fa[j][i] = fa[fa[j][i - 1]][i - 1];
}
}
for (rg int i = 1; i <= m; i++) {
rg int l, r, g;
q[i].id = i;
cin >> l >> r >> q[i].a >> q[i].b;
g = LCA(l, r);
if (g == l || g == r) {
q[i].l = in[l];
q[i].r = in[r];
q[i].extra = 0;
} else {
q[i].extra = g;
if (out[l] <= in[r]) {
q[i].l = out[l];
q[i].r = in[r];
} else {
q[i].l = out[r];
q[i].r = in[l];
}
}
if (q[i].l > q[i].r) swap(q[i].l, q[i].r);
}
sort(q + 1, q + m + 1, cmp);
rg int now_l = 1, now_r = 0;
for (rg int i = 1; i <= m; i++) {
while (q[i].l < now_l) update(--now_l);
while (q[i].r > now_r) update(++now_r);
while (q[i].l > now_l) update(now_l++);
while (q[i].r < now_r) update(now_r--);
if (q[i].a != q[i].b && cnt[q[i].a] && cnt[q[i].b]) {
ans[q[i].id] = res - 1;
} else {
ans[q[i].id] = res;
}
if (q[i].extra && !cnt[a[q[i].extra]]) ans[q[i].id]++;
}
for (rg int i = 1; i <= m; i++) {
cout << ans[i] << "\n";
}
return qwq;
}
4.树上带修莫队
例题9:糖果公园
题面:
分析:
无他,将带修莫队与树上莫队相结合就能得到。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long
using namespace std;
const int N = 2e5 + 3;
struct node {
int l, r, tim, id, extra;
} q[N];
vector<int> e[N];
int size, n, m, qq, v[N], col[N], w[N];
int b[N];
ll ans[N], res;
int tim, in[N], out[N], order[N << 1], dep[N], fa[N][21];
int pos[N], pre[N], then[N], cc[N], tot, cnt[N];
bool vis[N];
inline bool cmp(node n1, node n2) {
if (b[n1.l] != b[n2.l]) return b[n1.l] < b[n2.l];
if (b[n1.r] != b[n2.r]) return b[n1.r] < b[n2.r];
return n1.tim < n2.tim;
}
inline void dfs(int u) {
in[u] = ++tim;
order[tim] = u;
for (rg int i = 0; i < e[u].size(); i++) {
rg int v = e[u][i];
if (v != fa[u][0]) {
fa[v][0] = u;
dep[v] = dep[u] + 1;
dfs(v);
}
}
out[u] = ++tim;
order[tim] = u;
}
inline int lca(int x, int y) {
if (dep[x] < dep[y]) swap(x, y);
for (rg int i = 20; i >= 0; i--) {
if (dep[fa[x][i]] >= dep[y]) x = fa[x][i];
}
if (x == y) return x;
for (rg int i = 20; i >= 0; i--) {
if (fa[x][i] != fa[y][i]) {
x = fa[x][i];
y = fa[y][i];
}
}
return fa[x][0];
}
inline void modify(int x) {
vis[x] = !vis[x];
if (!vis[x]) {
res -= 1ll * w[cnt[col[x]]] * v[col[x]];
--cnt[col[x]];
} else {
++cnt[col[x]];
res += 1ll * w[cnt[col[x]]] * v[col[x]];
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m >> qq;
for (rg int i = 1; i <= m; i++) cin >> v[i];
for (rg int i = 1; i <= n; i++) cin >> w[i];
for (rg int i = 1; i < n; i++) {
rg int u, v;
cin >> u >> v;
e[u].push_back(v);
e[v].push_back(u);
}
dep[1] = 1;
dfs(1);
for (rg int i = 1; i <= 20; i++) {
for (rg int j = 1; j <= n; j++) {
fa[j][i] = fa[fa[j][i - 1]][i - 1];
}
}
size = 3000;
for (rg int i = 1; i <= (n << 1); i++) {
b[i] = (i - 1) / size + 1;
}
for (rg int i = 1; i <= n; i++) {
cin >> col[i];
cc[i] = col[i];
}
rg int T = 0, opt, x, y;
for (rg int i = 1; i <= qq; i++) {
cin >> opt >> x >> y;
if (opt == 1) {
rg int g = lca(x, y);
q[++tot].tim = T;
q[tot].id = tot;
if (x == g || y == g) {
q[tot].l = in[x];
q[tot].r = in[y];
q[tot].extra = 0;
} else {
q[tot].extra = g;
if (out[x] <= in[y]) {
q[tot].l = out[x];
q[tot].r = in[y];
} else {
q[tot].l = out[y];
q[tot].r = in[x];
}
}
if (q[tot].l > q[tot].r) swap(q[tot].l, q[tot].r);
} else {
++T;
pos[T] = x;
pre[T] = cc[x];
cc[x] = then[T] = y;
}
}
sort(q + 1, q + tot + 1, cmp);
rg int now_l = 1, now_r = 0, now_t = 0;
for (rg int i = 1; i <= tot; i++) {
while (q[i].l < now_l) modify(order[--now_l]);
while (q[i].r > now_r) modify(order[++now_r]);
while (q[i].l > now_l) modify(order[now_l++]);
while (q[i].r < now_r) modify(order[now_r--]);
while (q[i].tim > now_t) {
now_t++;
if (vis[pos[now_t]]) { //要修改的位置只被计算了一次,修改才会对答案产生影响
modify(pos[now_t]);
col[pos[now_t]] = then[now_t];
modify(pos[now_t]);
} else {
col[pos[now_t]] = then[now_t];
}
}
while (q[i].tim < now_t) {
if (vis[pos[now_t]]) {
modify(pos[now_t]);
col[pos[now_t]] = pre[now_t];
modify(pos[now_t]);
} else {
col[pos[now_t]] = pre[now_t];
}
now_t--;
}
ans[q[i].id] = res;
if (q[i].extra) ans[q[i].id] += 1ll * w[cnt[col[q[i].extra]] + 1] * v[col[q[i].extra]];
}
for (rg int i = 1; i <= tot; i++) {
cout << ans[i] << "\n";
}
return qwq;
}
例题10:Haruna's Breakfast
前置知识:
mex
mex,即求最小的没有出现的自然数。
例如,mex(1,2,0,3)=4,mex(2,1,3)=0
引入1:
在区间求mex前,我们先来思考考虑这样的问题:
实现一个数据结构来支持:
(1)添加一个数到集合中
(2)查询这个集合的mex
我们可以开一个vis数组,表示某个数字是否出现。初次有个下标指向0。
当我们添加一个数的时候,就\(vis[i]=1\)。
当查询mex的时候,直接暴力向上,找到第一个i,其\(vis[i]=0\)。
这样我们发现,如果我们有n此操作,下表最多移动n次,总复杂度为\(O(n)\)。
我们发现,长度为n的数组,mex最多为n,那么对于值域很大的题目,我们直接将\(a[i]>n\)的数都变成n+1。
引入2:
那如果我们在上述操作中添加一个删除操作呢?
我们可以维护一个set,表示未出现的数的集合,初始\(set=[0,1,2,3,\cdots,n]\)
当添加一个新的数,他就出现过了,所以我们把它从set中删除。
如果删除操作使得一个数没有出现过,就把他添加到set。
那么查询mex就直接查询set中的最小值即可。
int cot[N];
set<int> st;
int m, op, x;
for (rg int i = 0; i < N; i++) st.insert(i);
cin >> m;
while (m--) {
cin >> op;
if (op == 0) { //添加
cin >> x;
if (cot[x] == 0) st.erase(x);
cot[x]++;
} else if (op == 1) { //查询
cout << *st.begin() << "\n";
} else { //删除
cin >> x;
if (cot[x] == 1) st.insert(x);
cot[x]--;
}
}
模拟:
a[] = 0 1 1 1 2 2 4 5 6
set{0,1,2,3,4,5,6}
now{}
add 1
because cot[1]==0, set.erase(1),cot[1]=1
set{0,2,3,4,5,6}
now{1}
add 1
because cot[1]==1, cot[1]=2
set{0,2,3,4,5,6}
now{1,1}
query
set.begin()=0
add 2
because cot[2]==0, set.erase(2),cot[2]=1
set{0,3,4,5,6}
now{1,1,2}
add 0
because sot[0]==0, set.erase(0),cot[0]=1
set{3,4,5,6}
now{1,1,2,0}
query
set.begin()=3
del 1
because cot[1]==2, cot[1]=1
set{3,4,5,6}
now{1,2,0}
del 1
because cot[1]==1, set.insert(1),cot[1]=0
set{1,3,4,5,6}
now{2,0}
query
set.begin()=1
例题11:Rmq Problem / mex
用\(cot[i]\)来记录i出现了多少次,同时还有个\(sum[i]\)表示第i个块内出现了多少个数。
查询的时候,我们找到第一个没有放满的块,然后在这一块内暴力地去找。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 2e5 + 3;
int n, m, bsz, tot;
int sum[N], cot[N], ans[N], a[N], b[N];
struct node {
int l, r, id;
} q[N];
inline bool cmp(node a1, node a2) {
if (b[a1.l] != b[a2.l]) return b[a1.l] < b[a2.l];
if (b[a1.l] & 1) return a1.r < a2.r;
return a1.r > a2.r;
}
inline void add(int x) {
cot[x]++;
if (cot[x] == 1) sum[b[x]]++;
}
inline void del(int x) {
cot[x]--;
if (cot[x] == 0) sum[b[x]]--;
}
inline int query() {
for (rg int i = 1; i <= tot; i++) {
if (sum[i] != bsz) {
for (rg int j = (i - 1) * bsz; j <= i * bsz - 1; j++) {
if (!cot[j]) return j;
}
}
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
bsz = sqrt(n);
tot = N / bsz + 1;
for (rg int i = 1; i <= n; i++) {
cin >> a[i];
}
for (rg int i = 1; i <= N; i++) {
b[i] = i / bsz + 1;
}
for (rg int i = 1; i<= n; i++) {
if (a[i] > 2e5) a[i] = 2e5 + 1;
}
for (rg int i = 1; i <= m; i++) {
cin >> q[i].l >> q[i].r;
q[i].id = i;
}
sort(q + 1, q + m + 1, cmp);
rg int now_l = 1, now_r = 0;
for (rg int i = 1; i <= m; i++) {
while (q[i].l < now_l) add(a[--now_l]);
while (q[i].r > now_r) add(a[++now_r]);
while (q[i].l > now_l) del(a[now_l++]);
while (q[i].r < now_r) del(a[now_r--]);
ans[q[i].id] = query();
}
for (rg int i = 1; i <= m; i++) {
cout << ans[i] << "\n";
}
return qwq;
}
回到 Haruna's Breakfast 这道题上来。
这道题其实就是在树上找mex。我们将链转化成序列即可。对于修改,加上tim维即可。
//(实在调不过去了,暂时先放一份RE代码在这吧)
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 100500;
int n, m, bsz, tot, tim, ret;
int a[N], b[N], in[N], out[N], order[N];
int dep[N], ans[N], fa[N][22];
int cot[N], sum[N];
bool vis[N];
struct node1 {
int l, r, time, id, extra;
} q[N];
int pos[N], pre[N], then[N], cc[N];
vector<int> e[N];
inline bool cmp(node1 a1, node1 a2) {
if (b[a1.l] != b[a2.l]) return b[a1.l] < b[a2.l];
if (b[a1.r] != b[a2.r]) return b[a1.r] < b[a2.r];
return a1.time < a2.time;
}
inline void dfs(int u) {
in[u] = ++tim;
order[tim] = u;
for (rg int i = 0; i < e[u].size(); i++) {
rg int v = e[u][i];
if (v != fa[u][0]) {
fa[v][0] = u;
dep[v] = dep[u] + 1;
dfs(v);
}
}
out[u] = ++tim;
order[tim] = u;
}
inline int lca(int x, int y) {
if (dep[x] < dep[y]) swap(x, y);
for (rg int i = 21; i >= 0; i--) {
if (dep[fa[x][i]] >= dep[y]) x = fa[x][i];
}
if (x == y) return x;
for (rg int i = 21; i >= 0; i--) {
if (fa[x][i] != fa[y][i]) {
x = fa[x][i];
y = fa[y][i];
}
}
return fa[x][0];
}
inline void modify(int x) {
vis[x] = !vis[x];
if (vis[x]) {
cot[a[x]]++;
if (cot[a[x]] == 1) sum[b[a[x]]]++;
} else {
cot[a[x]]--;
if (cot[a[x]] == 0) sum[b[a[x]]]--;
}
}
inline int query() {
for (rg int i = 1; i <= tot; i++) {
if (sum[i] != bsz) {
for (rg int j = (i - 1) * bsz; j <= min(n, i * bsz - 1); j++) {
if (!cot[j]) return j;
}
}
}
}
int main() {
cin >> n >> m;
bsz = sqrt(n);
tot = n / bsz;
if (n % bsz) tot++;
for (rg int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
if (a[i] > 5e4) a[i] = 5e4 + 1;
cc[i] = a[i];
}
for (rg int i = 1; i < n; i++) {
rg int u, v;
scanf("%d %d", &u, &v);
e[u].push_back(v);
e[v].push_back(u);
}
dep[1] = 1;
dfs(1);
for (rg int i = 1; i <= 21; i++) {
for (rg int j = 1; j <= n; j++) {
fa[j][i] = fa[fa[j][i - 1]][i - 1];
}
}
for (rg int i = 1; i <= 5e4 + 1; i++) {
b[i] = i / bsz + 1;
}
rg int T, opt, x, y;
for (rg int i = 1; i <= m; i++) {
cin >> opt >> x >> y;
if (opt == 1) {
rg int g = lca(x, y);
q[++ret].time = T;
q[ret].id = ret;
if (x == g || y == g) {
q[ret].l = in[x];
q[ret].r = in[y];
q[ret].extra = 0;
} else {
q[ret].extra = g;
if (out[x] <= in[y]) {
q[ret].l = out[x];
q[ret].r = in[y];
} else {
q[ret].l = out[y];
q[ret].r = in[x];
}
}
if (q[ret].l > q[ret].r) swap(q[ret].l, q[ret].r);
} else {
++T;
pos[T] = x;
pre[T] = cc[x];
if (y > 5e4) y = 5e4 + 1;
cc[x] = then[T] = y;
}
}
sort(q + 1, q + ret + 1, cmp);
rg int now_l = 1, now_r = 0, now_t = 0;
for (rg int i = 1; i <= ret; i++) {
while (q[i].l < now_l) modify(order[--now_l]);
while (q[i].r > now_r) modify(order[++now_r]);
while (q[i].l > now_l) modify(order[now_l++]);
while (q[i].r < now_r) modify(order[now_r--]);
while (q[i].time > now_t) {
now_t++;
if (vis[pos[now_t]]) {
modify(pos[now_t]);
a[pos[now_t]] = then[now_t];
modify(pos[now_t]);
} else {
a[pos[now_t]] = then[now_t];
}
}
while (q[i].time < now_t) {
if (vis[pos[now_t]]) {
modify(pos[now_t]);
a[pos[now_t]] = pre[now_t];
modify(pos[now_t]);
} else {
a[pos[now_t]] = pre[now_t];
}
now_t--;
}
if (q[i].extra) {
cot[a[q[i].extra]]++;
if (cot[a[q[i].extra]] == 1) sum[b[a[q[i].extra]]]++;
}
ans[q[i].id] = query();
}
for (rg int i = 1; i <= ret; i++) {
printf("%d\n", ans[i]);
}
return qwq;
}
5.回滚莫队
有些题目在区间转移的时候,可能会出现增加或删除无法实现的问题。
在只有增加不可实现或只有删除不可实现的时候,就可以使用回滚莫队在\((n\sqrt m)\)的时间内解决问题。
回滚莫队的核心思想就是:既然只能实现一个操作,那么就使用一个操作,剩下的交给回滚解决。
回滚莫队分为只使用增加操作的回滚莫队和只使用删除操作的回滚莫队。两者只在算法实现上有一点区别。
例题12:历史研究
对原序列进行分块,对询问按以左端点所属块编号升序为第一关键字,右端点升序为第二关键字的排序方式。
按顺序处理询问:
(1)如果询问左端点所属块B和上一个询问左端点所属块的不同,那么将莫队区间的左端点初始化为B的右端点加1,将莫队区间的右端点初始化为B的右端点;
(2)如果询问的左右端点所属的块相同,那么直接扫描区间回答询问;
(3)如果询问的左右端点所属的块不同:
1.如果询问的右端点大于莫队区间的右端点,那么不断扩展右端点直至莫队区间的右端点等于询问的右端点;
2.不断扩展莫队区间的左端点直至莫队区间的左端点等于询问的左端点;
3.回答询问;
4.撤销莫队区间左端点的改动,使莫队区间的左端点回滚到B的右端点加。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long
using namespace std;
const int N = 1e5 + 3;
int n, qq;
int a[N], t[N], m;
struct node {
int l, r, id;
} q[N];
int b[N], L[N], R[N], bsz, tot;
int cnt[N], __cnt[N];
ll ans[N];
bool cmp(node a1, node a2) {
if (b[a1.l] != b[a2.l]) return b[a1.l] < b[a2.l];
return a1.r < a2.r;
}
inline void add(int v, ll& res) {
++cnt[v];
res = max(res, 1ll * cnt[v] * t[v]);
}
inline void del(int v) {
--cnt[v];
}
int main() {
scanf("%d %d", &n, &qq);
for (rg int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
t[++m] = a[i];
}
for (rg int i = 1; i <= qq; i++) {
scanf("%d %d", &q[i].l, &q[i].r);
q[i].id = i;
}
bsz = sqrt(n);
tot = n / bsz;
if (n % bsz) tot++;
for (rg int i = 1; i <= tot; i++) {
L[i] = (i - 1) * bsz + 1;
R[i] = i * bsz;
}
R[tot] = n;
for (rg int i = 1; i <= tot; i++) {
for (rg int j = L[i]; j <= R[i]; j++) {
b[j] = i;
}
}
sort(q + 1, q + qq + 1, cmp);
//离散化
sort(t + 1, t + m + 1);
m = unique(t + 1, t + m + 1) - (t + 1);
for (rg int i = 1; i <= n; i++) {
//a[i]在t[]中的位置,效果等同于离散化
a[i] = lower_bound(t + 1, t + m + 1, a[i]) - t;
}
rg int now_l = 1, now_r = 0, last_block = 0, __l; //__l为记录now_l要回滚到的左端点
rg ll res = 0, tmp;
for (rg int i = 1; i <= qq; i++) {
//询问的左右端点属于一个块则暴力扫描回答
if (b[q[i].l] == b[q[i].r]) {
for (rg int j = q[i].l; j <= q[i].r; j++) ++__cnt[a[j]];
for (rg int j = q[i].l; j <= q[i].r; j++) {
ans[q[i].id] = max(ans[q[i].id], 1ll * t[a[j]] * __cnt[a[j]]);
}
for (rg int j = q[i].l; j <= q[i].r; j++) --__cnt[a[j]];
continue;
}
//访问到了新的块则重新初始化莫队区间
if (b[q[i].l] != last_block) {
while (R[b[q[i].l]] < now_r) del(a[now_r--]);
while (R[b[q[i].l]] + 1 > now_l) del(a[now_l++]);
res = 0;
last_block = b[q[i].l];
}
//扩展右端点
while (q[i].r > now_r) add(a[++now_r], res);
__l = now_l;
tmp = res;
//扩展左端点
while (q[i].l < __l) add(a[--__l], tmp);
ans[q[i].id] = tmp;
//回滚
while (__l < now_l) del(a[__l++]);
}
for (rg int i = 1; i <= qq; i++) {
printf("%lld\n", ans[i]);
}
return qwq;
}
例题13:permu
我们以值为下标维护两个数组\(lb[i],rb[i]\)表示\(<i\)(即“左侧”)和\(>i\)(即“右侧”)的连续段长度,当我们加入一个值i的时候,会产生一个长度为\(lb[i]+rb[i]+1\)的连续段,可以用来更新答案。同时,我们需要更新答案。同时,我们需要更新\(lb,rb\)。对于i两端的值来说,我们不需要修改每一个值的\(lb,rb\),只需要修改边界的就可以了,因为下一次插入值w的时候,只有当w落在某个连续段的边界上,我们才需要更新答案,而更新的答案只与段边界\(lb,rb\)有关。
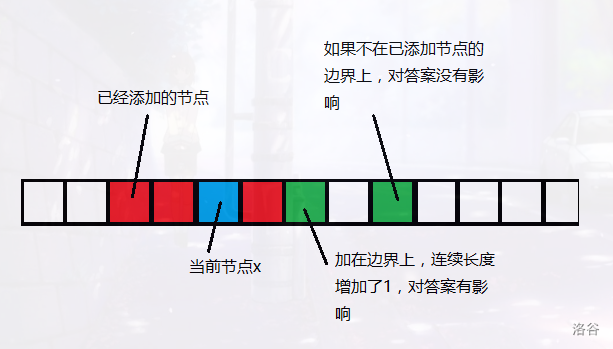
然后考虑如何莫队处理:
我们以左端点所在块编号为第一关键字,右端点为第二关键字排序。对于一个块中的所有询问,我们发现r是递增的,所以不用撤销。而l不一定是递增的,我们要考虑如何撤销某个添加值的操作。
对于某一块,初始r设为块的右端点,然后每个询问先将r往右移,处理r和l不在同一块的询问。然后处理询问在块内之间的部分,直接暴力把询问的块内部分的所有点添加进去。修改前把原来\(lb,rb\)的值记录下来,保存在栈里面。处理完这个询问之后再复原。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 5e4 + 3;
int n, m;
int a[N], b[N], bsz;
int ans[N], lb[N], rb[N];
struct node1 {
int l, r, id;
} q[N];
struct node2 {
int type; //记录是哪个数组修改,1则是lb,2则是rb
int pos, val;
} st[N];
bool cmp(node1 a1, node1 a2) {
if (b[a1.l] != b[a2.l]) return b[a1.l] < b[a2.l];
return a1.r < a2.r;
}
inline void add(int x, int& res) {
lb[x] = lb[x - 1] + 1;
rb[x] = rb[x + 1] + 1;
rg int len = lb[x] + rb[x] - 1;
res = max(res, len);
//对连续段的边界进行修改
lb[x + rb[x] - 1] = len;
rb[x - lb[x] + 1] = len;
}
inline void del(int x) {
lb[x] = rb[x] = 0;
}
int main() {
scanf("%d %d", &n, &m);
bsz = sqrt(n);
for (rg int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
b[i] = (i - 1) / bsz + 1;
}
for (rg int i = 1; i <= m; i++) {
scanf("%d %d", &q[i].l, &q[i].r);
q[i].id = i;
}
sort(q + 1, q + m + 1, cmp);
rg int now_l = 1, now_r = 0, res = 0, tmp, last_block = 0;
for (rg int i = 1; i <= m; i++) {
if (b[q[i].l] != last_block) { //新的块,初始化
res = 0;
for (rg int i = 1; i <= n; i++) lb[i] = rb[i] = 0;
now_r = b[q[i].l] * bsz;
last_block = b[q[i].l];
}
while (q[i].r > now_r) add(a[++now_r], res); //如果l,r不在同一个块,把r在块外部分加入
tmp = res;
rg int top = 0;
for (rg int j = q[i].l; j <= min(q[i].r, b[q[i].l] * bsz); j++) {
lb[a[j]] = lb[a[j] - 1] + 1;
rb[a[j]] = rb[a[j] + 1] + 1;
rg int len = lb[a[j]] + rb[a[j]] - 1;
st[++top] = {1, a[j] + rb[a[j]] - 1, lb[a[j] + rb[a[j]] - 1]};
st[++top] = {2, a[j] - lb[a[j]] + 1, rb[a[j] - lb[a[j]] + 1]};
lb[a[j] + rb[a[j]] - 1] = len;
rb[a[j] - lb[a[j]] + 1] = len;
tmp = max(tmp, len);
}
for (rg int j = top; j >= 1; j--) { //撤销对连续段端点的修改
if (st[j].type == 1) lb[st[j].pos] = st[j].val;
else rb[st[j].pos] = st[j].val;
}
for (rg int j = q[i].l; j <= min(q[i].r, b[q[i].l] * bsz); j++) { //撤销新加入的点对lb,rb的修改
del(a[j]);
}
ans[q[i].id] = tmp;
}
for (rg int i = 1; i <= m; i++) {
printf("%d\n", ans[i]);
}
return qwq;
}