首页 > 其他分享 >基环树

基环树

时间：2024-06-11 22:46:51浏览次数：22  
标签：环上 int 基环树 rg 节点 define

基环树

1.定义

基环树是一个由n个点及n条边组成的连通图，其比树多出一条边，所以称作基环树。

2.分类

基环树分为无向基环树和有向基环树。
而有向基环树又分为内向基环树和外向基环树。
内向基环树，即每个点出度为1的基环树；外向基环树，即每个点入度为1的基环树。

3.解决方式

对于有关基环树的问题，一般有两种解决方式：

  • 1.将环断开一条边，作普通树处理。
  • 2.将环上的每个节点的子树的信息合并到该节点上，最后对环进行处理

无向图上的基环树：

可以将这种有n个节点、n条边的无向连通图看作在一棵树上加了一条边，形成了一张恰好包含一个环的图。

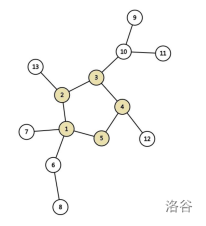
当然，如果不保证联通，那么有n个节点、n条边的无向图也有可能是一个基环树森林。

有向图上的基环树：

内向树：每个节点出度为1。

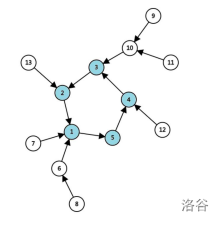
外向树：每个节点入度为1。

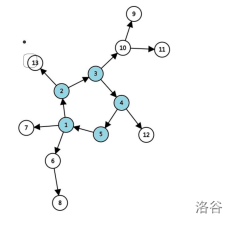
例题1：[ZJOI2008] 骑士

算法：环套树dp（基环树）

若原图是树，经典dp做法：\(f[i][0/1]\)表示i点选或不选的最大能力值和，则：\(f[i][0]=\sum max(f[j][0]，f[j][1])\)，\(f[i][1]=\sum f[j][0]+a[i]\)，其中\(j=son[i]\)。
找环：dfs到访问过的点，标记环上的一条边。
破环：和普通树上dp唯一的区别是，标记两端不能同时为1，所以从两端A开始分别进行一次树形dp，最后\(ans=max(f[A][0],f[B][0])\)。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long
using namespace std;
const int N = 1e6 + 3, inf = 2e9;
int siz[N];
int r1, r2;  //断掉边的两个节点 
int p[N];
int vis[N], flag;
ll ans, f[N][2];
int head[N], edge_cnt = 1;
struct edge {
	int to, nxt;
} e[N << 1];
inline void add(int x, int y) {
	e[++edge_cnt].nxt = head[x];
	e[edge_cnt].to = y;
	head[x] = edge_cnt;
}
inline void dfs1(int u, int fath) {
	vis[u] = 1;
	siz[++siz[0]] = u;
	for (rg int i = head[u]; i; i = e[i].nxt) {
		rg int v = e[i].to;
		if (v == fath) continue;
		if (!vis[v]) dfs1(v, u);
		else if (vis[v] && !flag) {
			flag = true;
			r1 = u;
			r2 = v;
		}
	}
}
inline void dfs2(int u, int fath) {
	f[u][0] = 0;
	f[u][1] = p[u];
	for (rg int i = head[u]; i; i = e[i].nxt) {
		rg int v = e[i].to;
		if (v && v != fath) {
			dfs2(v, u);
			f[u][1] += f[v][0];
			f[u][0] += max(f[v][0], f[v][1]);
		}
	}
}
int n;
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin >> n;
	rg int x, y;
	for (rg int i = 1; i <= n; i++) {
		cin >> p[i] >> x;
		add(x, i);
		add(i, x);
	}
	for (rg int i = 1; i <= n; i++) {
		if (!vis[i]) {
			siz[0] = 0;
			flag = false;
			dfs1(i, 0);
			if (!flag) {
				rg int rt = siz[1];
				dfs2(rt, 0);
				ans += max(f[rt][0], f[rt][1]);
			} else {
				rg ll maxv = -inf;
				for (rg int j = head[r1]; j; j = e[j].nxt) {
					if (e[j].to == r2) {
						e[j].to = 0;
						e[j ^ 1].to = 0;
						break;
					}
				}
				dfs2(r1, 0);
				maxv = max(maxv, f[r1][0]);
				dfs2(r2, 0);
				maxv = max(maxv, f[r2][0]);
				ans += maxv;
			}
		}
	}
	cout << ans << "\n";
	return qwq;
}

例题2：[NOIP2018 提高组] 旅行

（1）当\(m=n-1\)时，即图中无环，为了保证字典序最小我们可以直接从1号节点开始搜索，每当我们搜到一个点，都可以把它所有能到的点放到一个小根堆里，然后从字典序最小的点开始枚举。当我们把整棵树遍历完的时候，即可得到所要求的解。
（2）如果\(m=n\)，即图中有环。思考一下可知，在我们遍历整个图的时候，环上总会有一条边不会被经过，所以我们可以枚举断哪一条边，对所有情况取最大值。又发现没有必要找环，直接枚举断哪条边就可以了。
剪枝优化：
1.如果要走的是断开边，就跳过不走。
2.发现路径不如之前优，就返回。

两种打法：
1.

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 5003;
int n, m, a, b;
vector<int> e[N];  //存边，链式前向星没法排序
pair<int, int> edge [N];  //记录边的两个端点
int du, dv, vis[N];
vector<int> path(N, N);  //记录走过的路径，初始全部赋为 N
int cnt, better;
inline bool dfs(int u) {
	if (!better) {  //若序号变大则回退，变小则走完 
		if (u > path[cnt]) return true;
		if (u < path[cnt]) better = 1;  //如果当前搜索的u更优，那后面就再也进不来if(!better) 
	}
	vis[u] = 1;
	path[cnt++] = u;
	for (rg int i = 0; i < e[u].size(); i++) {
		rg int v = e[u][i];
		if (vis[v]) continue;
		if ((u == du && v == dv) || (u == dv && v == du)) continue;
		//如果dfs(v)为true，就说明按着v往下搜就不优了，直接截停
		if (dfs(v)) return true;
	}
	return false;
}
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin >> n >> m;
	for (rg int i = 1; i <= m; i++) {
		cin >> a >> b;
		e[a].push_back(b);
		e[b].push_back(a);
		edge[i] = {a, b};
	}
	for (rg int i = 1; i <= n; i++) {  //预处理每个邻边 
		sort(e[i].begin(), e[i].end());
	}
	if (n == m + 1) {  //如果是一棵树 
		dfs(1);
	} else {
		for (rg int i = 1; i <= m; i++) {  //枚举断边
			du = edge[i].first;
			dv = edge[i].second;
			memset(vis, 0, sizeof(vis));
			cnt = better = 0;
			dfs(1);
		}
	}
	for (rg int i = 0; i < n; i++) {
		cout << path[i] << " ";
	}
	return qwq;
}

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 5003;
int n, m;
int ans[N], step, in[N];
int du, dv, res[N];
bool vis[N], edge[N], del[N][N];
vector<int> e[N];
inline void dfs(int u) {  //找路径
	if (step > n) return ;
	ans[++step] = u;
	vis[u] = 1;
	for (rg int i = 0; i < e[u].size(); i++) {
		rg int v = e[u][i];
		if (vis[v] || (du == u && dv == v) || (du == v && dv == u)) continue;
		dfs(v);
	}
}
inline void find_circle() {  //将非环上的点标记edge[i]=true 
	queue<int> q;
	for (rg int i = 1; i <= n; i++) {
		//入度为1的点一定不在环上 
		if (in[i] == 1) q.push(i); 
	}
	while (!q.empty()) {
		rg int u = q.front();
		q.pop();
		edge[u] = 1;  //在树上的边，也就是不在环上
		for (rg int i = 0; i < e[u].size(); i++) {
			rg int v = e[u][i];
			in[v]--;
			//入度为1的边不可能为环上的边 
			if (in[v] == 1) q.push(v);
		}
	}
}
inline bool check() {  //如果当前路径更优，返回true 
	//第一次检查 
	if (res[1] == 0) return true;
	for (rg int i = 1; i <= n; i++) {
		if (ans[i] == res[i]) continue;
		if (ans[i] < res[i]) return true;
		return false;
	}
}
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin >> n >> m;
	for (rg int i = 1; i <= m; i++) {
		rg int a, b;
		cin >> a >> b;
		e[a].push_back(b);
		e[b].push_back(a);
		in[a]++;
		in[b]++;
	}
	for (rg int i = 1; i <= n; i++) {
		sort(e[i].begin(), e[i].end());
	}
	if (m == n - 1) {
		dfs(1);
		for (rg int i = 1; i <= n; i++) {
			cout << ans[i] << " ";
		}
		return qwq;
	}
	//有环，将环上的边依次删除，在dfs
	find_circle();
	for (rg int u = 1; u <= n; u++) {  //枚举环上的边 
		if (edge[u]) continue;
		for (rg int i = 0; i < e[u].size(); i++) {
			rg int v = e[u][i];
			if (edge[v]) continue;  //在树上的点
			du = u;
			dv = v;
			if (del[du][dv]) continue;  //删过的边不再删
			del[du][dv] = del[dv][du] = 1;
			memset(vis, 0, sizeof(vis));
			step = 0;
			dfs(1);
			if (check()) {
				for (rg int i = 1; i <= n; i++) {
					res[i] = ans[i];  //更新 
				}
			}
		}
	}
	for (rg int i = 1; i <= n; i++) {
		cout << res[i] << " ";
	}
	return qwq;
}

例题3：[IOI2008] Island

显然，构成的图是一个基环树森林。
根据题意，要使经过的总路径最长且每棵基环树都只能经过一次，则答案就是每棵基环树的直径的和。
于是考虑求基环树的直径。
我们用g数组存环上节点的子树的直径，f数组存环上节点的子树上从该节点开始的最长链的长度。
基环树的直径有下面两种情况：

  • 1.在环的某一棵子树上。
  • 2.经过环，在环的两棵子树上。

对于第一种情况，答案即为g数组中的最大值。
对于第二种情况，我们从任意一个环上的点开始，将整个环转化为一条链（比如1，2，3组成的环会变成[1,2,3]），然后从左往右扫。我们注意到，对于两个点i和j（\(i<j\)），从i到j事实上可以有两条不同的路径（如\(1\to2\)可以是\(1\to2\)或\(1\to3\to2\)）。因此我们令链上路径长度的前缀和为pre，环的路径总长度为len，于是两种路径的长度分别为：
\(ret1=max\{f_i+f_j+(pre_i-pre_j)\}=max\{f_i-pre_i+f_j+pre_j\}\)
\(ret2=max\{f_i+f_j+len-(pre_j-pre_i)\}=max\{f_i+pre_i+f_j-pre_j + len\}\)
我们发现i和j的贡献在上面两个式子中是独立的，我们可以记一下当前下标小于j的所有i中最大的\(f-pre_i\)（m1）和\(f_i+pre_i\)（m2），然后每次新扫到一个点就可以用m1和m2更新。
那么最后的答案就是：\(ans=max\{ret1,ret2,g_i\}\)
而我们在遍历完一个环之前并没法拿到这个环的长度len，因此我们更新\(ret2\)时不用加上len，最后遍历完再给ret2加上len即可。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
using namespace std;
const int N = 1e6 + 3;
int n;
int t[N], w[N];
int deg[N];
int f[N], g[N];
inline void get() {  //计算环上节点的f[]和g[] 
	queue<int> q;
	for (rg int i = 1; i <= n; i++) {
		if (!deg[i]) q.push(i);
	}
	while (!q.empty()) {
		rg int u = q.front();
		q.pop();
		rg int ret = f[u] + w[u];
		g[t[u]] = max(g[t[u]], max(f[t[u]] + ret, g[u]));
		f[t[u]] = max(f[t[u]], ret);
		deg[t[u]]--;
		if (!deg[t[u]]) q.push(t[u]);
	}
}
inline int get_d(int u) {
	rg int lu = u;
	rg int res = LLONG_MIN, m1 = f[u], m2 = f[u], pre = w[u], ret1 = g[u], ret2 = LLONG_MIN;
	u = t[u];
	while (u != lu) {
		deg[u] = 0;
		ret1 = max(ret1, m1 + f[u] + pre);
		ret2 = max(ret2, m2 + f[u] - pre);
		res = max(res, g[u]);
		m1 = max(m1, f[u] - pre);
		m2 = max(m2, f[u] + pre);
		pre += w[u];
		u = t[u];
	}
	return max(max(ret1, ret2 + pre), res);
}
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin >> n;
	for (rg int i = 1; i <= n; i++) {
		cin >> t[i] >> w[i];
		deg[t[i]]++;
	}
	get();
	rg int ans = 0;
	for (rg int i = 1; i <= n; i++) {
		if (deg[i]) ans += get_d(i);
	}
	cout << ans << "\n";
	return qwq;
}

例题4：[POI2012] RAN-Rendezvous

很明显是基环树\(+\)lca。
因为是基环树森林，所以如果a和b不在同一棵基环树上，直接输出\(-1 -1\)。
可以利用并查集维护连通性，但在拓扑找环求环长时可以顺便维护。
而当a和b在同一棵基环树上时有两种情况：

  • 1.他们在同一棵环上节点的子树上。此时直接倍增求lca即可。
  • 2.他们不在同一棵环上节点的子树上，此时lca要么是a对应的环上节点，要么是b对应的环上节点，对两种情况按照条件对比，输出更合适的即可。

对于第一种情况，我们可以建反图，对于环上节点向其子树跑dfs，将每一个节点打上“属于哪个根”的标记，即可判断两个节点是否在同一子树。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 5e5 + 3;
int n, m, tot;
int in[N];
int dot[N];  //标记该节点属于哪个环上节点
int fa[N][21], dep[N];  //倍增求lca 
int kuai[N], siz[N], step[N];  //标记该环上节点属于哪个连通块，连通块包含的环上节点数，这个连通块中的编号 
vector<int> e[N];
inline void find_circle() {
	queue<int> q;
	for (rg int i = 1; i <= n; i++) {
		if (!in[i]) q.push(i);
	}
	while (!q.empty()) {
		rg int u = q.front();
		q.pop();
		rg int v = fa[u][0];
		in[v]--;
		if (!in[v]) q.push(v);
	}
}
inline void get_dot(int u, int fath, int rt) {
	dot[u] = rt;
	for (rg int i = 0; i < e[u].size(); i++) {
		rg int v = e[u][i];
		if (in[v] || v == fath) continue;
		dep[v] = dep[u] + 1;
		get_dot(v, u, rt);
	}
}
inline void get_kuai(int u, int id, int cnt) {
	if (step[u]) return ;
	kuai[u] = id;
	siz[id]++;
	step[u] = cnt;
	get_kuai(fa[u][0], id, cnt + 1);
}
inline void init() {
	for (rg int i = 1; i <= 20; i++) {
		for (rg int j = 1; j <= n; j++) {
			fa[j][i] = fa[fa[j][i - 1]][i - 1];
		}
	}
}
inline int lca(int x, int y) {
	if (dep[x] < dep[y]) swap(x, y);
	for (rg int i = 20; i >= 0; i--) {
		if (dep[fa[x][i]] >= dep[y]) x = fa[x][i];
	}
	if (x == y) return y;
	for (rg int i = 20; i >= 0; i--) {
		if (fa[x][i] != fa[y][i]) {
			x = fa[x][i];
			y = fa[y][i];
		}
	}
	return fa[x][0];
}
inline bool check(int a, int b, int c, int d) {
	if (max(a, b) != max(c, d)) return max(a, b) < max(c, d);
	if (min(a, b) != min(c, d)) return min(a, b) < min(c, d);
	return a >= b;
} 
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin >> n >> m;
	for (rg int i = 1; i <= n; i++) {
		rg int a;
		cin >> a;
		e[a].push_back(i);
		fa[i][0] = a;
		in[a]++;
	}
	find_circle();
	for (rg int i = 1; i <= n; i++) {
		if (in[i]) {
			get_dot(i, 0, i);
			if (!step[i]) get_kuai(i, ++tot, 1);
		}
	}
	init();
	while (m--) {
		rg int a, b;
		cin >> a >> b;
		if (kuai[dot[a]] != kuai[dot[b]]) {
			cout << -1 << " " << -1 << "\n";
		}  else if (dot[a] == dot[b]) {
			rg int LCA = lca(a, b);
			cout << dep[a] - dep[LCA] << " " << dep[b] - dep[LCA] << "\n";
		} else {
			rg int t1 = dot[a], t2 = dot[b];
			rg int ans1 = dep[a] + (step[t2] - step[t1] + siz[kuai[t1]]) % siz[kuai[t1]];  //b所在子树的根到a的距离 = a所在子树的根到a的距离 + 两根的距离 
			rg int ans2 = dep[b] + (step[t1] - step[t2] + siz[kuai[t1]]) % siz[kuai[t1]];  //a所在子树的根到b的距离 = b所在子树的根到b的距离 + 两根的距离 
			if (check(dep[a], ans2, ans1, dep[b])) cout << dep[a] << " " << ans2 << "\n";
			else cout << ans1 << " " << dep[b] << "\n";
		}
	}
	return qwq;
}

例题5：创世纪

法一：贪心

1.如果一个点的入度为0（即为叶子节点），那么这个点不可能被投放，所以删去它与父节点并把答案+1（父节点可放）
2.对于一个含a个节点的环（不与其他节点相连），对答案的贡献为a>>1。
拓扑排序过程中按1处理，排序后剩下的环按2处理即可。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 1e6 + 3;
int n, fa[N], in[N], ans;
bool vis[N];
queue<int> q;
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin >> n;
	for (rg int i = 1; i <= n; i++) {
		cin >> fa[i];
		in[fa[i]]++; 
	}
	//操作1：拓扑排序 
	for (rg int i = 1; i <= n; i++) {
		if (!in[i]) q.push(i);
	}
	while (!q.empty()) {
		rg int u = q.front();
		q.pop();
		if (vis[u]) continue;
		vis[u] = true;
		rg int f = fa[u];
		in[f]--;
		if (!in[f]) q.push(f);
		if (!vis[f]) {
			vis[f] = true;
			ans++;
			f = fa[f];
			in[f]--;
			if (!in[f]) q.push(f);
		}
	}
	//操作2： 
	for (rg int i = 1; i <= n; i++) {
		if (!vis[i]) {
			rg int cnt = 1;  //统计环的大小 
			rg int u = fa[i];
			vis[u] = true;
			while (u != i) {
				cnt++;
				vis[u] = true;
				u = fa[u];
			}
			ans += cnt >> 1;
		}
	}
	cout << ans << "\n";
	return qwq;
}

法二：树形dp

将限制条件看成每个点有一条出边，所以就是一个内向基环树森林。找出每个基环树的环，然后对于树的部分，跑dp，设状态\(f[x][0/1]\)为选或不选x节点，则：

\(f[x][0] = \displaystyle\sum_{y\in son[x]}max\{f[y][0],f[y][1]\}\)

\(f[x][1] = \displaystyle\sum_{y\in son[x]}max\{f[y][0],f[y][1]\}+(全选了f[y][1])?\sum_{y\in son[x]}max\{f[y][0]-f[y][1]\}\) (如果限制x的节点全部被投放，那么将最不优的拿回)

在环上很难处理，因为每个节点取不取既和环上前一个结点有关也和下一个节点有关，这个环上dp转移是有后效性的。
采用基环树dp一个常用手段：断环成树。断环时，应注意断开的环上两个点相互影响的关系。
比如此题，每一个点可能会影响后一个点的选择，分两种情况：
1.此点不影响下一个点，则断开后，以此点为根做树形dp，那么两点互不影响，题目条件都成立。
2.若考虑有影响，则需要这个点不选，让下一个点可以随便选儿子的两个状态较大值而不用担心没有指向它的不选的点。
综上，断边后做两次dp即可。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 1e6 + 3, inf = 2147483647;
int n, rt, too, flag, ans, res, ban;
bool vis[N];
int f[N][2];
int head[N], nxt[N << 1], to[N << 1], tot = 1;
inline void add(int x, int y) {
	to[++tot] = y;
	nxt[tot] = head[x];
	head[x] = tot;
}
inline void dfs(int u) {
	vis[u] = true;
	for (rg int i = head[u]; i; i = nxt[i]) {
		if (i & 1) continue;
		rg int v = to[i];
		if (vis[v]) {
			rt = u;
			too = v;
			ban = i;
			return ;
		} else dfs(v);
	}
}
inline void dp1(int u, int fath) {
	vis[u] = true;
	rg bool flag = true;
	f[u][1] = 1;
	for (rg int i = head[u]; i; i = nxt[i]) {
		rg int v = to[i];
		if (v == fath || i == ban || i == (ban ^ 1)) continue;  //当前边是断掉的边，跳过 
		dp1(v, u);
		if (f[v][0] < f[v][1]) {
			f[u][0] += f[v][1];
			f[u][1] += f[v][1];
		} else {
			f[u][0] += f[v][0];
			f[u][1] += f[v][0];
			flag = false;
		}
	}
	if (flag) {  //限制u的边全都投放了
		rg int tmp = -inf;
		for (rg int i = head[u]; i; i = nxt[i]) {
			rg int v = to[i];
			if (v == fath || i == ban || i == (ban ^ 1)) continue;
			tmp = max(tmp, f[v][0] - f[v][1]);
		}
		f[u][1] += tmp;
	}
}
inline void dp2(int u, int fath) {
	rg bool flag = true;
	f[u][0] = 0;
	f[u][1] = 1;
	for (rg int i = head[u]; i; i = nxt[i]) {
		rg int v = to[i];
		if (v == fath || i == ban || i == (ban ^ 1)) continue;
		dp2(v, u);
		if (f[v][0] < f[v][1]) {
			f[u][0] += f[v][1];
			f[u][1] += f[v][1];
		} else {
			f[u][0] += f[v][0];
			f[u][1] += f[v][0];
			flag = false;
		}
	}
	if (flag && u != too) {
		rg int tmp = -inf;
		for (rg int i = head[u]; i; i = nxt[i]) {
			rg int v = to[i];
			if (v == fath || i == ban || i == (ban ^ 1)) continue;
			tmp = max(tmp, f[v][0] - f[v][1]);
		}
		f[u][1] += tmp;
	}
}
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin >> n;
	for (rg int i = 1; i <= n; i++) {
		rg int a;
		cin >> a;
		add(i, a);
		add(a, i);
	}
	for (rg int i = 1; i <= n; i++) {
		res = 0;
		if (!vis[i]) {
			dfs(i);
			dp1(rt, 0);  //不考虑断环之后根对断点有影响 
			res = max(f[rt][0], f[rt][1]);
			dp2(rt, 0);  //考虑断环之后根对断点有影响（即不选根）
			res = max(res, f[rt][0]);
			ans += res;
		}
	}
	cout << ans << "\n";
	return qwq;
}

标签：环上,int,基环树,rg,节点,define
From： https://www.cnblogs.com/Baiyj/p/18242907

相关文章

  • 基环树
    基环树的定义为：一个有向或无向图中，只含有一个环的图，形式化的表达为：关于这种形状关键点主要在于找环，那么我们可以一步一步的去寻找，当这个点走着走着走到了某个环里，我们可以直接遍历整个环，然后打个标记，这样环就找到了具体的例题：E-ReachabilityinFunctionalGraph本题就是一......
  • 基环树找环
    abc167_dTeleporter#include<bits/stdc++.h>#defineptprintf(">>>")#definemid(((l)+(r))/2)usingnamespacestd;typedeflonglongll;typedeflongdoubleld;constllN=1e6+10,inf=1e18+10,mod=1e9+7;vector<ll>G[N];map&......
  • 置换 & 基环树题
    T1Statement给一个长度为\(n(\le10^5)\)的排列\(\{a_i\}\)。求一个排列\(\{b_i\}\)，使得\(a_i=b_{b_i}\)，或输出不存在。Solution先把所有排列变成置换对于任意排列\(\{p_i\}\)，它转成置换后都是\(i\top_i\)，故有\(i\top_i\top_{p_i}\top_{p_{p_i}}\to...\)所以所有......
  • 基环树算法总结
    基环树算法总结一、什么是基环树基环树，顾名思义，有两个要素：环和树。因此，基环树就是一棵树的一个节点，扩成一个环，做题时，多棵基环树组成的基环树森林，常以如下方式出现：每个点只有一个出边。每个点只有一个入边。图中一共有\(n\)个点，\(n\)条边。那么，基环树类型的题目应该怎......
  • 基环树
    byDuck.感觉都是神秘乱搞。一般的处理方式：把整个环当成根。断环。CF711DDirectedRoads正难则反，考虑统计成环的数量。我们先把环搜出来，那么环上的边只能有全部顺时针或者全部逆时针两种方向，环外的边任意。设环长为\(L\)，那么就有\(2^{n-L}\times2\)种有环的情况，从而......
  • 基环树小结
    基环树就是根节点基于环生长的一棵树，特点是\(n\)个节点\(n\)条边。如果\(n\)个节点\(n\)条边的图不联通那么是一个基环森林。很好证明，\(n\)个点\(n-1\)条边的联通图仅能是一棵树，现在从任一点引出一条边到任一点，由于两点先前一定联通，则在连接后原路径上的任意两点均有......
  • 关于基环树的一切
    观前须知笔者的博客主页声明本文使用CCBY-NC-SA4.0许可。本文为笔者在OI学习中的复习向学习笔记。部分内容会比较简略。如有好的习题会不断补充。知识简介定义基环树是一个有\(n\)个点\(n\)条边的连通图。因为树有\(n\)个点\(n-1\)条边。所以基环树可以......
  • 基环树
    1基环树概念1.1定义首先，基环树并不是一颗严格的树。它是一张由\(n\)个节点，\(n\)条边组成的图。1.2无向联通图上的基环树首先，一棵树有\(n\)个节点，\(n-1\)条边。那么基环树就可以看做是在一棵树上加了一条边，这样多出了一个环（因此基环树也被称作环套树）。如下图所示：1.......
  • 基环树学习笔记
    基环树学习笔记定义基环树指的是一张有\(n\)个节点和\(n\)条边的图，如果不保证连通的话，那么整张图是一张基环树森林。并且如果将环上的任意一条边去除，那么整棵基环树会成为一棵普通的树。分类基环树有以下几种特殊情况，也是题目中较多出现的。基环内向树指的是在一棵有向......
  • 基环树学习笔记
    1.定义基环树，又称环套树，n个点n条边，也就是一棵树多一条边，形成唯一的环，这是保证这n个点n条边构成的是一个连通图的时候才是唯一环，如果图不连通但是每个连通块点数都等于边数的时候这个图就是一个基环树森林，可以有多个环如果一张有向弱连通图每个点的入度都为1，则称它是一棵基环外......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99