正态性检验是利用观测数据判断总体是否服从正态分布的检验,它是统计判决中重要的一种特殊的拟合优度假设检验。正态性检验的方法有很多,以下列举几种常用的方法:
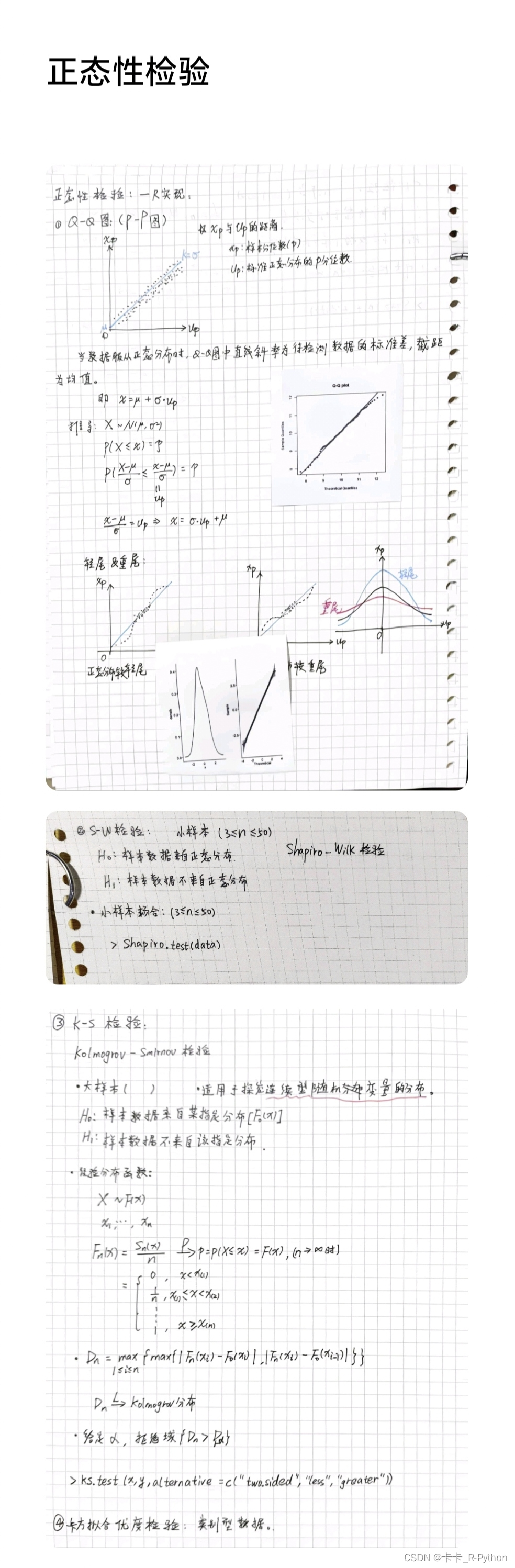
1. **图示法**:比如分位数-分位数图(Quantile-Quantile Plot,Q-Q图),这是一种常见的图示方法。通过对数据直方图曲线与对应μ、σ的标准正态分布曲线之间进行回归,计算出拟合优度来说明两条曲线之间的拟合程度。
2. **正态概率纸法**:一种通过绘制数据点在正态概率纸上的位置来判断数据是否服从正态分布的方法。
3. **夏皮罗-威尔克检验法(Shapiro-Wilk test)**:一种基于样本数据的顺序和大小来评估数据正态性的检验方法。
4. **科尔莫戈罗夫检验法**:又被称为D检验法,它基于经验分布函数与理论分布函数之间的最大差异进行检验。
5. **偏度-峰度检验法**:根据数据的偏度和峰度与正态分布的偏度和峰度(均为0)进行比较,从而判断数据的正态性。这种方法包括偏度检验、峰度检验以及偏度和峰度的联合检验。
在实际应用中,正态性检验的目的是判断一组观测值是否来自正态总体,具有正态分布的特性。
标签:偏度,检验,检验法,峰度,正态性,正态分布 From: https://blog.csdn.net/2301_76574743/article/details/139609087