Solution Set #2

标签：左子 连通 Set text 复杂度 Solution 考虑 节点

发电语录，被班主任注意到，并被公示到 \(\text{whk}\) 家长群了。

发电语录，被班主任注意到，并被公示到 \(\text{whk}\) 家长群了。

发电语录，被班主任注意到，并被公示到 \(\text{whk}\) 家长群了。

20.「NOI2022」冒泡排序

离散化掉 \(V_i\) 显然没有影响。

• 基础性质：若 \(i<j\) 且 \(a_i>a_j\)，若交换 \(a_i,a_j\) 后序列依然合法，则 \(a_i,a_j\) 交换不劣。证明显然：只考虑 \([i+1,j-1]\) 的点与 \(i,j\) 的影响，那么 \(a_i<a_j\) 一定不劣于 \(a_i\ge a_j\)。

由「基础性质」可以得到，未被区间限制的点单独拉出来一定构成一个不降序列。

考虑每个点都有一个下限 \(\text{lim}_i\)。可以在 \(O(n\alpha(n))\) 的复杂度，使用序列并查集优化跳跃完成维护。

【特殊性质 B/C】

考虑一个区间的限制无交，单独找出来这个区间，由「基础性质」，第一个数 \(=V_i\)，并且后面保持不降，一定不劣。这个点锁定之后，考虑确定后面的值。

逆序对考虑倒着维护，放在前面的，维护后面的值。若未确定，那么令 \(c_t\) 表示 \(a_i=t\) 会向后产生多少的逆序对，那么直接取出关于限制条件的后缀的 \(\argmin\) 即可。确定之后，再去对 \(c_{a_i+1\sim m}\) 进行后缀加即可。

【特殊性质 A】

• \(\text{min}=0\) 的意思是不全为 \(1\)。

• \(\text{min}=1\) 的意思就是全是 \(1\)。

• 相交且包含的第一类区间，\(I_1\subseteq I_2\) 时，需要保留 \(I_1\)。

• 相交且包含的第二类区间，\(I_1\subseteq I_2\) 时，需要保留 \(I_2\)。

我们希望 \(a_i=1,a_j=0,i<j\) 的东西尽量少。全是 \(1\) 的限制有很多。而逆序对的关键因素是 \(0\)，所以感性上少放 \(0\) 就赢了。两种限制的意思是，确定某些位置必须是 \(0\)。

倒序扫描线。考虑当且仅当不放 \(0\) 就会不合法时，再放 \(0\)。确定这些 \(0\) 后就是自由填，同样用线段树维护。

【正解】

考虑一个值 \(V\) 被若干区间限制，并且有若干点的下限是 \(V\)，记这个点集是 \(S\)。我们希望这些区间导出一个具有许多更多限制的不交区间，对这些区间进行性质 A，得到必须为 \(V\) 的点值集合 \(T\)。

得到所有固定点以及每个点的下界后，套用【特殊性质 B/C】的做法。数据结构只需要维护区间加以及区间 \(\argmin\)，线段树即可。

时间复杂度 \(O(n\log n)\)。

21. LOJ2552 / 「CTSC2018」假面

考虑 \(f_{i,j}\)：第 \(i\) 个人剩余 \(j\) 血的概率。这个非常好维护。每次都是单点操作。

操作 2 就是求出每个人存活的概率 \(\text{alive}_i=1-f_{i,0}\)。

令 \(g_{i,j}\) 表示除了 \(i\)，还有 \(j\) 个人存活的概率。答案就是：

\[\sum_{i=1}^k(1-f_{i,0})\sum_{j=0}^{k-1}\dfrac{g_{i,j}}{j+1} \]

除了 \(i\) 的限制很烦人。考虑求 \(T_i\) 表示 \(i\) 个人存活的概率。这个可以扫的时候顺便求出来。

然后 \(g_{i,j}=\dfrac{T_j-g_{i,j-1}\times (1-f_{i,0})}{f_{i,0}}\)。

随便做了，懒得算复杂度。

22. 「GDKOI-S 2023」树

如果在子树内，显然 \(\text{dis}\) 可以转化成 \(\triangle \text{dep}\)。那么在同一个 \(\text{dep}\) 的点，考虑第二维的 \(\text{dfn}\) 属性，那么我们可以考虑，求解 \(u\) 子树内 \(\text{dfn}\) 的最大值的点，减去前一个 \(u\)，以容斥掉未计算的部分。每一个 \(u\) 管辖的就是每层的一段前缀。每层的最后一个点就会构成 \(u\) 子树的最右链。

令 \(\text{rs}(u)\) 表示 \(u\) 最右边的儿子，用来考虑 \(u\) 管辖的子树的边界。

定义【\(k\) 级邻域】是 \(\text{dep}_v\in[\text{dep}_u,\text{dep}_u+k)\)，且在 \(v\) 的管辖范围之中的点。

考虑倍增维护，\(f_{u,i}\) 表示 \(u\) 的 \(2^i\) 级邻域的答案。考虑 \(f_{u,i-1}\to f_{u,i}\) 的变化：\(u\) 的 \(2^{i-1}\) 级的右儿子的 \(2^{i-1}\) 级邻域，在 \(i-1\) 位多异或了一个 \(1\)。还需要维护 \(\text{size}_u\) 表示 \(u\) 的管辖区域的大小，以及在此管辖区域中，有多少个点的点值在第 \(i\) 位为一。容易求出，有多少个点，在 \(i-1\) 位 \(1\to 0\)，以及 \(0\to 1\)。

考虑 \(k\) 级邻域的答案，先往下跳右子到 \(v\)，然后考虑从 \(u\) 往下走，去减掉 \(v\) 的管辖区域，来求出某一位的变化量。

时间复杂度 \(O(n\log n)\)。

23.「联合省选 2024」魔法手杖

记录 \(p_q\) 表示 \(p\) 在二进制表示下的第 \(q\) 位。

二分答案就是 trie 树乱搞，朴素实现判定 \(O(nk)\)，总复杂度就是 \(O(nk^2)\)，这样有 \(72\) 分。

二分，好像可以只存 trie 树的 \(1,2\) 度点，从而做到 \(O(n)\) 判定。弗如直接嗯贪。做法来自 @tzl_dedicatus545，膜拜。

考虑对于 \(a_i\) 建立一棵 trie 树，显然我们要从高往低确定答案。对于每个节点，记录子树中的 \(a_i\) 的 \(\min\) 以及 \(b_i\) 的和。考虑当前是处理 \(ans\) 的第 \(d\) 位，先讨论 \(x\) 的第 \(d\) 位能否是 \(0\)。

如果 \(x_d=0\)，那么要想让 \(ans_d=1\)，就必须把左子树全部放入 \(S\)，不然 \(\text{xor}\) 出来这位就是是 \(0\)，我们要保证这样做是更优的，就是令 \(ans_{t\ge d}\) 都是 \(1\)，\(x_{t\ge d}\) 都是 \(0\) 时可以更优才考虑这种情况。那么把左边放入 \(S\) 就需要里面的 \(b_i\) 的和的代价，记录剩余体力然后进行判定即可。接下来就是递归右子树即可。

\(x_d=1\) 的讨论基本一致。

如果 \(ans_d\) 确定不能是 \(1\)，那么可以把右边全扔进 \(S\)，只考虑左子的情况，对称情况同理，接着递归即可。

最多访问 trie 树上的 \(O(nk)\) 个节点，复杂度是 \(O(nk)\)。

24.「联合省选 2024」迷宫守卫

考虑从 Alice 的视角来做这道题，Bob 在能选择的时候都会去往小的走。

这题其实是最大化字典序：

• 给某些点用一些代价删去往右走的可能性，然后让剩下来的所有排列的最小的那个字典序最大。

考虑对于字典序最大化或者最小化的问题，逐位地确定下来答案。花了很大的代价让这一位必须更大，然后后面都改不了了，显然是更优的。

这样做，需要确定下来当前选 \(v\) 作为当前位的答案时，和前面已经确定的位造成的总贡献是否 \(\ge k\)。假设当前在对子树 \(u\) 中的点确定顺序，那么这一部分在 \(Q\) 中会构成一段区间，考虑对于 \(u\) 找出 \(u\) 中所有的叶子节点的值 \(q_v\)，对其进行排序后扔进一个 \(\text{vector}\) 里面，那么我们就是要倒序判断这个 \(\text{vector}\) 里面，最先去找 \(v\) 是否合法。

Alice 要想让 Bob 第一个就去走 \(v\)，肯定要付出一些代价。考虑用 \(f_{u,x}\) 表示 \(u\) 中子树的叶子节点中，Bob 到达 \(u\) 时，要想让 Bob 第一个就去走 \(x\)，Alice 需要付出的最小代价。

那么其实我们必须先要求出来 \(f_{u,x}\)。突然想起来，学线段树合并优化 \(\text{DP}\) 的时候，依赖于子树叶子节点，状态数显然是对的，所以是有前途的。

令 \(\text{size}_u\) 表示 \(u\) 中的叶子节点个数，那么总状态数其实就是 \(\sum \text{size}_i=n2^n\)。

字典序这玩意只关心相对大小，那么这个 dp 也可以转化成：\(f_{u,x}\)，Bob 抵达 \(u\) 时，Bob 第一个会去走叶子节点的 \(q_j\) 的第 \(x\) 小的代价。

初始状态显然是 \(f_{\text{leaf},1}=0\)。考虑对于这棵满二叉树，进行树上 \(\text{DP}\) 的状态合并。

先维护出来上文提到的那个 \(\text{vector}\)，对它进行排序后，对于左子和右子分别计算其是第 \(rk_i\) 小的，可以双指针维护。

然后考虑计算 \(f_{u,i}\) 的值，需要分别讨论 \(i\) 在左还是右：

第 \(i\) 小来自于左子：

若这个位置 \(i\) 属于左子，不仅需要原来在左子的代价，而且需要保证 Bob 不会往右边跑，有两种选择：

• 唤醒怪物，剪掉右子，代价是 \(w_u\)。
• 对于右子排名更高的，先处理某一个，考虑让右子排名 \(>i\) 的所有的 \(\min\) 为 \(T\)。

转移为 \(f_{u,i}\leftarrow f_{\text{lson},\text{rev}(i)}+\min(T,w_u)\)。

第 \(i\) 小来自于右子：

若这个位置 \(i\) 属于左子，需要原来在右子的代价，以及不让 Bob 往左边跑，压根不用唤醒怪物：

• 对于左子排名更高的，先处理某一个，考虑让左子排名 \(>i\) 的所有的 \(\min\) 为 \(T\)。

转移为 \(f_{u,i}\leftarrow f_{\text{rson},\text{rev}(i)}+T\)。

记录对于排名 \(>i\) 的左子的 \(f_{\text{lson},j}\) 的 \(\min\) 是 \(A\)，同理设右子的是 \(B\)。倒序双指针扫一下就可以维护。

这部分的时间复杂度是 \(O(n^22^n)\)，多一个 \(n\) 是因为有排序的瓶颈，也就是说要考虑 \(T(N)=2T(\frac{N}{2})+O(N\log^2 N)\)。

回到上一部分之前，考虑求出来 \(f_{u,i}\) 之后怎么做。考虑先贪心：对于当前子树 \(u\)，确认接下来先去走哪里，算出来当前要去 \(v\) 的最小代价，设 \(v\) 是 \(u\) 子树中 \(q_j\) 排序的第 \(i\) 大。

在 \(u\) 里面考虑就是要 \(f_{u,i}\)，但是还要考虑别的，预先已经有的代价 \(B\)，以及 \(\text{fa}_u\) 不往右走做出的代价 \(w_{\text{fa}_u}\)，比较上一步的信息 \(k\)，如果 \(v<k\)，注意到本题标号的特殊性，可以判定是哪边下来的，就需要做出来 \(w_{\text{fa}_u}\) 的代价，以保证它不往右边走。

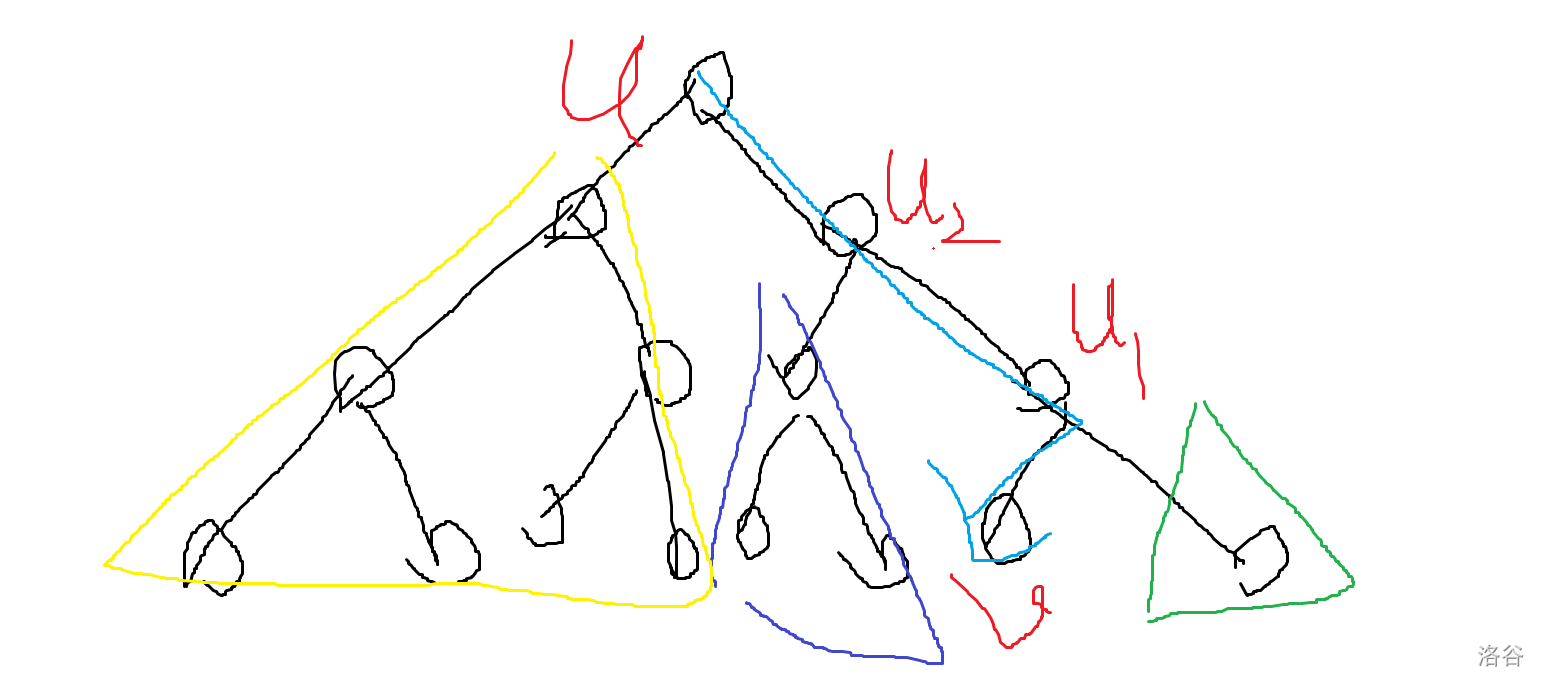
考虑找到 \(v\) 之后，去递归处理黄色，紫色，绿色的子问题。根是从底往上去考虑。每次递归就需要预留一定的代价。递归子问题 \(t\) 的子树时，考虑从 \(B\) 中删去一些代价，当做这个子问题还未处理：当往右边递归时，额外考虑 \(w_{u_i}\)，保证可以走到这里。然后都需要考虑 \(>v\) 的点 \(j\) 的 \(f_{t,j}\)，这些需要取 \(\min\)。

处理好已有代价后，直接递归处理即可。正确性是最优决策不会被替换的。时间复杂度 \(O(2^nn^2)\)。

25.「联合省选 2024」重塑时光

显然要将概率转计数。

考虑对于 \(m\) 条限制建立 \(\text{DAG}\)，记这个图是 \(G=(V,E)\)。直接不好算，考虑计算，对于给定的拆分方式，有多少个排列合法。这样它就变成 counting 了。

判定一组合法，考虑对于 \(k+1\) 个集合 \(S_i\)，\(S_i\) 内部顺序一定是 \(G\) 对于 \(S_i\) 导出子图的拓扑序。同时 \(k+1\) 个集合之间的边不能形成环。

显然对于每个集合的内部，顺序没有太大影响，如果确定了每个集合的构成，直接乘上这些的拓扑序个数即可。记 \(g_S\) 表示 \(G\) 对于 \(S\) 的导出子图的拓扑序个数，直接枚举首位进行转移即可，这个可以做到 \(O(n2^n)\)。

定义一组集合划分的权值，是所有集合拓扑序个数以及顺序的乘积。

考虑集合之间的影响，仍然放在 \(G\) 上处理。先把空的去了，最后直接组合数一乘就行。设对于 \(f_{S,i}\) 是 \(S\) 中划分了 \(i\) 个非空集合的权值和。

音乐课想到这里想了半天不会，然后就摆烂了，wssb。

\(\textbf{DAG}\) 这种东西，一定要特殊考虑下，无入度 / 无出度 的点。

考虑钦定子集 \(T\subset S\) 使得 \(T\) 是无出度的，作为这个 \(S\) 所谓的叶子。钦定 的作用是，可以后面直接乘上容斥系数 \((-1)^{|T|+1}\)，最后求和就是我们想要的东西。这个 \(T\) 中的划分方式，考虑分为了 \(x\) 个集合，这 \(x\) 个集合一定满足其是独立集，即没有边直接相连。

接下来就不难想到，考虑 \(dp_{S,i}\) 为 \(S\) 的导出子图，划分为 \(i\) 个非空独立集的所有方案的权值和，枚举子集 \(T\) 然后判定与余下部分双向独立，再转移，即：\(f_{S\setminus T,i-1}\times g_{T}\)。这个显然可以做到 \(O(n3^n)\)。

考虑回过头来求 \(f_{S,i}\)，需要枚举叶子独立集 \(T\)，以及其大小，需要考虑补集的所有大小，所以这部分的复杂度是 \(O(3^nn^2)\)。

算出来所有的 \(f_{S,i}\) 后，再求一下总合法方案数。再除以总方案数 \(\dfrac{(n+k)!}{k!}\) 即可。操作之间有序无序其实无所谓，因为 \(k!\) 总会被消掉。

总时间复杂度 \(O(3^nn^2)\)，由于没啥常数直接就过了。

26.「联合省选 2024」季风

考虑枚举 \(m\bmod n\) 的值，会有一堆绝对值不等式，零点分段然后取个交就完事了，不用 \(\text{int128}\)。

27.「联合省选 2023」城市建造

无向图连通块问题考虑建立圆方树，用边双点双的性质去分析。

考虑将题目的限制转化成：断开 \(E'\) 中的边后，\(V'\) 中的所有点两两不连通，因此构成 \(|V'|\) 个连通块。

性质 1：若 \(u,v\in V'\)，则对于所有 \(u\to v\) 的路径，其中的每个点都要选择。

为了保证 \(u,v\) 不连通，所有的路径都得被干掉。

性质 2：边双中的边同时取或者不取。

考虑一个边双连通分量中的所有边，如果并没有被取干净，那么 \(G-E'\) 会让 \(V'\) 中的某两个点，来自同一个点双的，连通。手玩可知：对一个边双，其中所有边要么全取要么不取。

性质 3：\(G'\) 本身构成一个连通块。

考虑在圆方树上刻画选择的情况，容易发现，将选择的方点染黑，那么各个连通块大小就是删去染黑方点后，各个部分圆点的个数。

由性质 3，染黑的方点一定是个连通块。

注意到连通块之差 \(\leq 1\)，那么方点的连通块一定会包含，关于圆点的重心 \(R\)。那么圆方树可以直接钦定 \(R\) 为根。

令 \(\text{size}(u)\) 表示 \(u\) 子树的圆点个数。

由性质 1,2,3，可以开始圆方树上 dp 了。

注意到单层 dp 的复杂度大概率是 \(O(n)\) 的，那么我们可以考虑在最外层枚举连通块的大小。\(k=0\) 时枚举都为 \(x\)，\(k=1\) 时枚举都在 \([x,x+1]\) 中，枚举量 \(O(\sqrt n)\)。

最外层在枚举 \(x\)。考虑 \(f_u\) 为在 \(u\) 的子树中删的方案数。转移时，我们把 圆方边 的情况统一放在圆点统计。

无论 \(k\)，方点的方案数一定都是子节点的 dp 值相乘。

考虑圆点 \(u\) 怎么选。

\(k=0\) 时：对于 \(\text{size}(v)<x\) 的所有点，必须和这个圆点 \(u\) 绑在一起。这些 \(\text{size}\) 的和必须是 \(x-1\)，否则无解。然后记录 \(\text{size}(v)\ge x\) 的所有 \(dp_v\) 的乘积就是 \(u\) 的方案数。因为这类的 \((u,v)\) 是必须断开的。

\(k=1\) 时：区别是：考虑 \(=x\) 的可以保留一个。依然是判定 \(\text{size}(v)<x\) 的子树大小和为 \(S\)，\(\text{size}(v)>x\) 的 \(dp_v\) 乘积为 \(T\)。

当 \(S=0\) 时，可以将 \(u\) 扔进 \(=x\) 的连通块，可以有额外贡献，有以下讨论：

对于 \(\text{size}(v)=x\) 的：考虑一共有 \(c_1\) 个，其中有 \(c_2\) 个不能单独放，也就是 \(dp_v=0\) 的一共有 \(c_2\) 个。显然 \(c_2>1\) 时就寄了，当 \(c_2=0\) 时，直接是 \(T\times c_1\)，否则当 \(c_2=1\) 时，有 \(T\) 种。

然后再乘上正常分讨：将 \(u\) 和 \(\text{size}(u)<S\) 的点 \(v\) 的扔一起的方案数。

• 对于 \(k=0\)，时间复杂度 \(O(nd(n))\)。
• 对于 \(k=1\)，时间复杂度 \(O(n\sqrt n)\)。

28.「NOI2023」桂花树

条件 \(1\) 等价于 \(1\sim n\) 在 \(T_2\) 的虚树就是 \(T\)，换而言之，所有的 \(n+1\sim m+1\) 就是在 \(T\) 上面「生长」出来的，可能是 \(T\) 上的枝条「分化」出了节点，然后在这些节点上开花。也有可能是在 \(T\) 的节点上「分裂」出节点。

• 所以为什么我生物 \(1.333\) 模比一模低了 \(10\) 分？？？

考虑条件二。很不好考虑，注意到 \(k\) 很小，提示我们去往 \(2^k\) 上去想。

\(\max\) 这个东西考虑强制钦定一维大于另一维。

考虑扫描线地从小到大加入节点 \(i\in [n+1,n+m]\)，那么所有原有的节点 \(j<i\) 都需要满足 \(\text{LCA}(i,j)\leq i+k\)。

考虑 \(k=0\) 的部分分怎么做。

• 在树上逐渐插入 \(n+1\sim n+m\) 的所有点，注意到所有的节点都需要与 \(i\) 在更小的节点相聚。那么 \(i\) 只能插入在每个边的中间，即「分化」，也可以直接「分裂」在某个点的下面。

• 每次都是同样的问题：已有 \(S\) 大小的树，可以插入在 \(S\) 个点下面，或者 \(S-1\) 条边中间。有 \(2S-1\) 个选择。

因此答案就是：\(\prod_{i=n}^{n+m-1}(2i-1)\)。

考虑 \(k>0\) 的问题是什么：

有些节点可以与 \(i\) 在更大的节点相聚。但是我们不能让直接让 \(i\) 挂在半空中，需要提前加入一个标号更大的点使得 \(i\) 与这棵树连通。

因此可以考虑虚树。我们只需要对虚树计数。每次的操作只有以下三种，并且当前已经至少加入 \([1,i-1]\) 的点：

• 挂在已有边上。进行「分化」。
• 挂在已有点上。进行「分裂」。
• 在已有边上，先分裂出一个标号更大的点 \(u\)，作为 \(i\) 与某些点的 \(\text{LCA}\)，然后再直接把 \(i\) 挂在 \(u\) 下面。

注意到 \(k\leq 10\)，因此可以考虑当前虚树的形态为 \([1,i]\cup S\) 中的点构成，其中 \(S\subseteq[i+1,i+k]\)。可以直接状压 dp 维护方案数。

时间复杂度 \(O(Tmk2^k)\)。

标签：左子,连通,Set,text,复杂度,Solution,考虑,节点
From： https://www.cnblogs.com/nullptr-qwq/p/18236460