6.6--链表

标签：head ListNode cur -- next 链表 6.6 节点

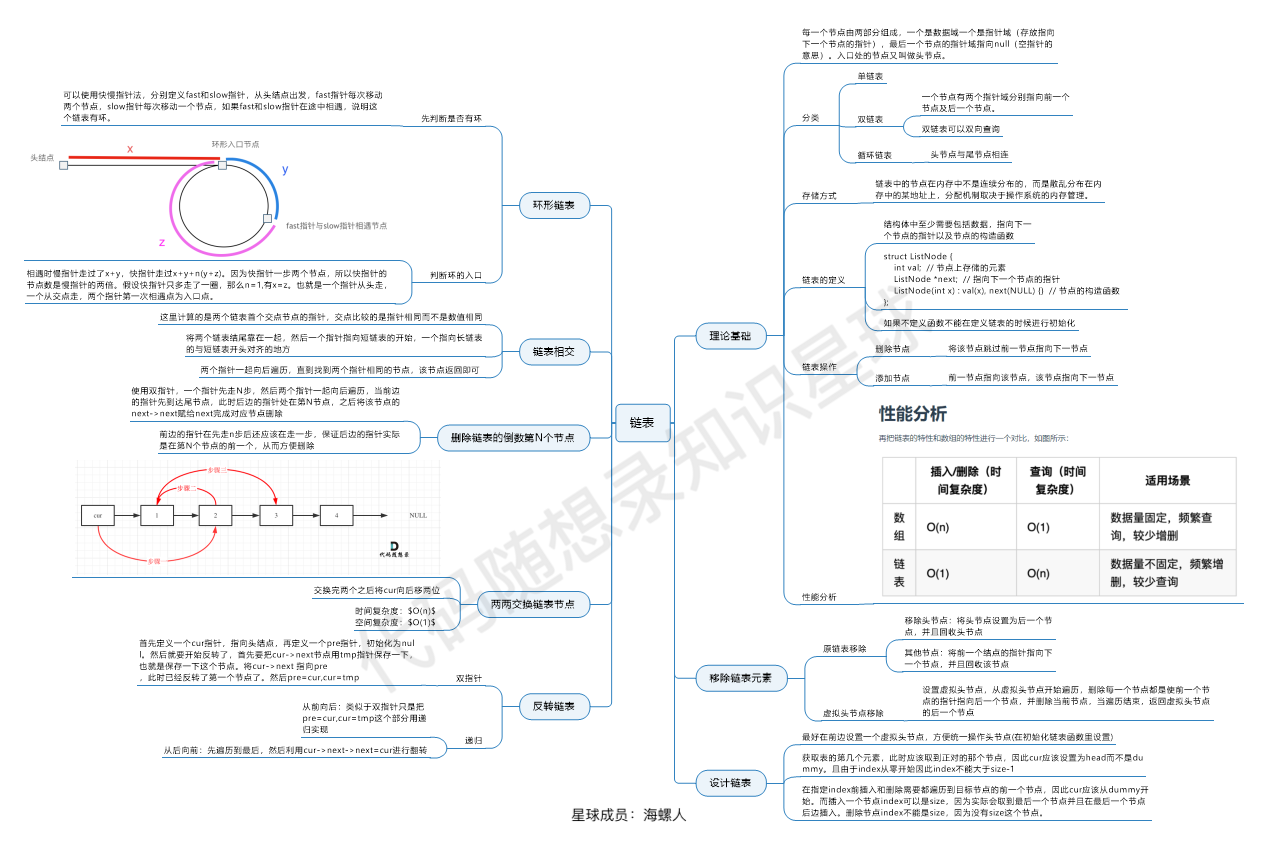
链表的定义

C++的定义链表节点方式，如下所示：

// 单链表
struct ListNode {
    int val;  // 节点上存储的元素
    ListNode *next;  // 指向下一个节点的指针
    ListNode(int x) : val(x), next(NULL) {}  // 节点的构造函数
};

不定义构造函数，C++默认生成一个构造函数，但是这个构造函数不会初始化任何成员变量，下面举两个例子：

通过自己定义构造函数初始化节点：

ListNode* head = new ListNode(5);

使用默认构造函数初始化节点：

ListNode* head = new ListNode();
head->val = 5;

所以如果不定义构造函数使用默认构造函数的话，在初始化的时候就不能直接给变量赋值！

链表的操作链表的操作

主要是增删

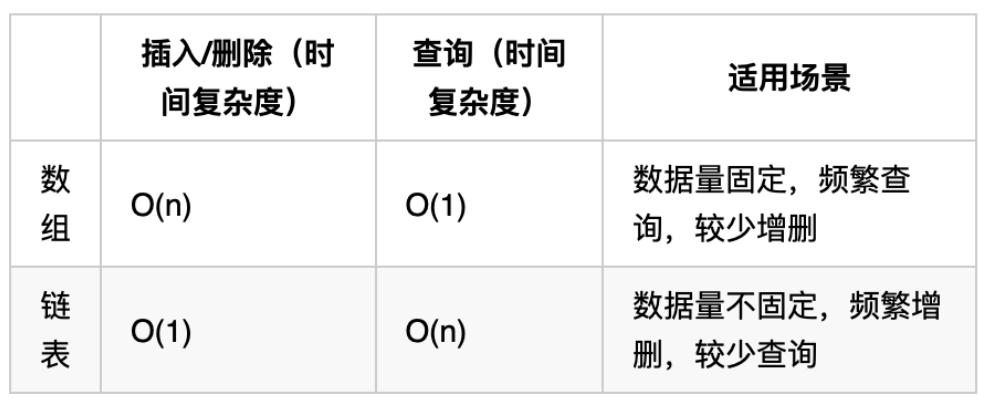
数组在定义的时候，长度就是固定的，如果想改动数组的长度，就需要重新定义一个新的数组。

链表的长度可以是不固定的，并且可以动态增删，适合数据量不固定，频繁增删，较少查询的场景。

链表-链表与数据性能对比

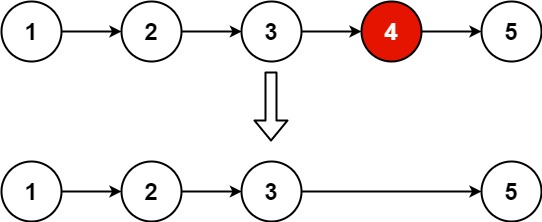
203.移除链表元素

题目描述：

给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回 新的头节点 。

示例 1：
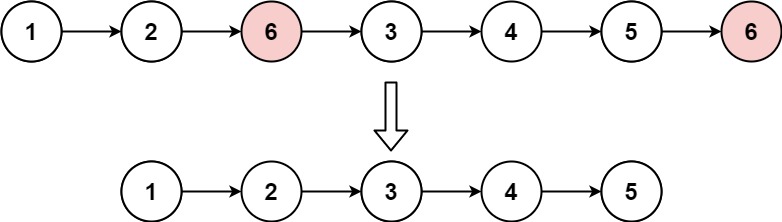
输入：head = [1,2,6,3,4,5,6], val = 6
输出：[1,2,3,4,5]
示例 2：
输入：head = [], val = 1
输出：[]
示例 3：
输入：head = [7,7,7,7], val = 7
输出：[]
提示：

列表中的节点数目在范围 [0, 104] 内

1 <= Node.val <= 50

0 <= val <= 50

思路：设置虚拟头结点：以一种统一的逻辑来移除链表的节点

移除头结点和移除其他节点的操作是不一样的，因为链表的其他节点都是通过前一个节点来移除当前节点，而头结点没有前一个节点。

所以头结点如何移除呢，其实只要将头结点向后移动一位就可以，这样就从链表中移除了一个头结点。

在写代码的时候也会发现，需要单独写一段逻辑来处理移除头结点的情况。

那么可不可以以一种统一的逻辑来移除链表的节点呢。

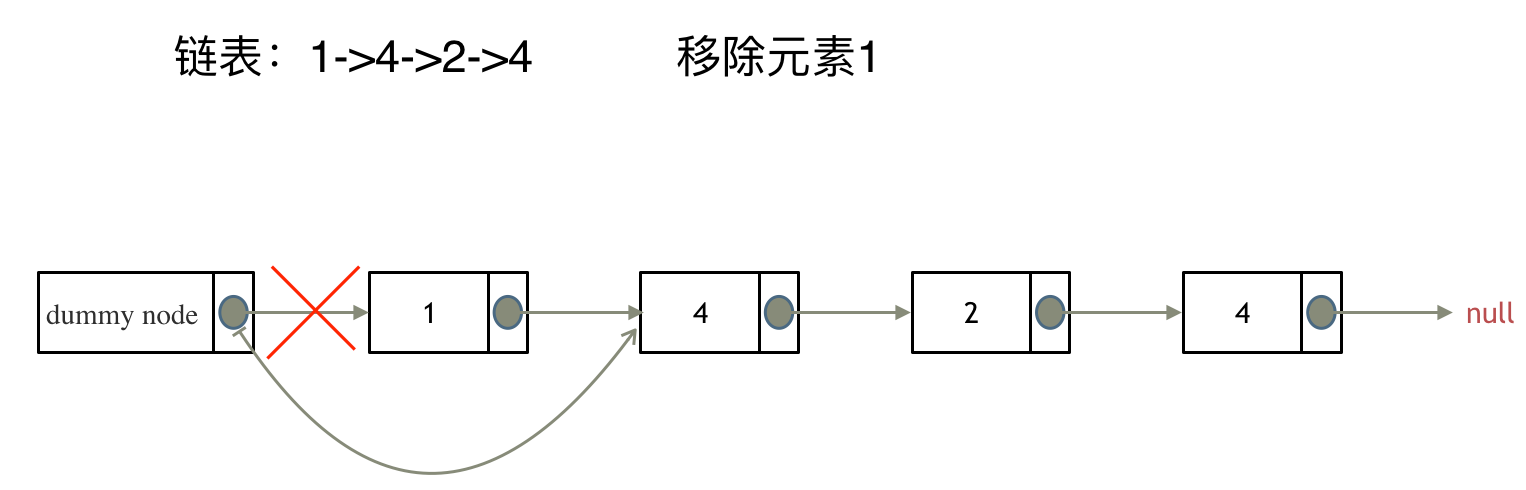
其实可以设置一个虚拟头结点，这样原链表的所有节点就都可以按照统一的方式进行移除了。

最后呢在题目中，return 头结点的时候，别忘了 return dummyNode->next;，这才是新的头结点

203_链表删除元素6

AC代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeElements(ListNode* head, int target) {
        ListNode* dummyHead = new ListNode(0);
        dummyHead-> next = head;

        ListNode* cur = dummyHead;
        while(cur->next != NULL){
          if(cur->next->val == target){
            ListNode* tmp = cur->next;
            cur->next = cur->next->next;
            delete tmp;
          }
          else  cur = cur->next;
        }
        head = dummyHead->next;
        delete dummyHead;
        return head;
    }
};

M:707.设计链表

题目描述：

你可以选择使用单链表或者双链表，设计并实现自己的链表。

单链表中的节点应该具备两个属性：val 和 next 。val 是当前节点的值，next 是指向下一个节点的指针/引用。

如果是双向链表，则还需要属性 prev 以指示链表中的上一个节点。假设链表中的所有节点下标从 0 开始。

实现 MyLinkedList 类：

MyLinkedList() 初始化 MyLinkedList 对象。

int get(int index) 获取链表中下标为 index 的节点的值。如果下标无效，则返回 -1 。

void addAtHead(int val) 将一个值为 val 的节点插入到链表中第一个元素之前。在插入完成后，新节点会成为链表的第一个节点。

void addAtTail(int val) 将一个值为 val 的节点追加到链表中作为链表的最后一个元素。

void addAtIndex(int index, int val) 将一个值为 val 的节点插入到链表中下标为 index 的节点之前。如果 index 等于链表的长度，那么该节点会被追加到链表的末尾。如果 index 比长度更大，该节点将 不会插入 到链表中。

void deleteAtIndex(int index) 如果下标有效，则删除链表中下标为 index 的节点。

示例：
输入
["MyLinkedList", "addAtHead", "addAtTail", "addAtIndex", "get", "deleteAtIndex", "get"]
[[], [1], [3], [1, 2], [1], [1], [1]]
输出
[null, null, null, null, 2, null, 3]

解释
MyLinkedList myLinkedList = new MyLinkedList();
myLinkedList.addAtHead(1);
myLinkedList.addAtTail(3);
myLinkedList.addAtIndex(1, 2);    // 链表变为 1->2->3
myLinkedList.get(1);              // 返回 2
myLinkedList.deleteAtIndex(1);    // 现在，链表变为 1->3
myLinkedList.get(1);              // 返回 3
提示：

0 <= index, val <= 1000

请不要使用内置的 LinkedList 库。

调用 get、addAtHead、addAtTail、addAtIndex 和 deleteAtIndex 的次数不超过 2000 。

思路：

这道题目设计链表的五个接口：

获取链表第index个节点的数值

在链表的最前面插入一个节点

在链表的最后面插入一个节点

在链表第index个节点前面插入一个节点

删除链表的第index个节点

可以说这五个接口，已经覆盖了链表的常见操作，是练习链表操作非常好的一道题目

链表操作的两种方式：

直接使用原来的链表来进行操作。

设置一个虚拟头结点在进行操作。

下面采用的设置一个虚拟头结点（这样更方便一些，大家看代码就会感受出来）。

AC代码：

class MyLinkedList {
public:
    // 定义链表节点结构体
    struct LinkedNode {
        int val;
        LinkedNode* next;
        LinkedNode(int val):val(val), next(nullptr){}
    };//结构体struct}后一定要加分号！！

    // 初始化链表
    MyLinkedList() {
        _dummyHead = new LinkedNode(0); // 这里定义的头结点 是一个虚拟头结点，而不是真正的链表头结点
        _size = 0;
    }

    // 获取到第index个节点数值，如果index是非法数值直接返回-1， 注意index是从0开始的，第0个节点就是头结点
    int get(int index) {
        if (index > (_size - 1) || index < 0) {
            return -1;
        }
        LinkedNode* cur = _dummyHead->next;
        while(index--){ // 如果--index 就会陷入死循环
            cur = cur->next;
        }
        return cur->val;
    }

    // 在链表最前面插入一个节点，插入完成后，新插入的节点为链表的新的头结点
    void addAtHead(int val) {
        LinkedNode* newNode = new LinkedNode(val);
        newNode->next = _dummyHead->next;
        _dummyHead->next = newNode;
        _size++;
    }

    // 在链表最后面添加一个节点
    void addAtTail(int val) {
        LinkedNode* newNode = new LinkedNode(val);
        LinkedNode* cur = _dummyHead;
        while(cur->next != nullptr){
            cur = cur->next;
        }
        cur->next = newNode;
        _size++;
    }

    // 在第index个节点之前插入一个新节点，例如index为0，那么新插入的节点为链表的新头节点。
    // 如果index 等于链表的长度，则说明是新插入的节点为链表的尾结点
    // 如果index大于链表的长度，则返回空
    // 如果index小于0，则在头部插入节点
    void addAtIndex(int index, int val) {

        if(index > _size) return;
        if(index < 0) index = 0;        
        LinkedNode* newNode = new LinkedNode(val);
        LinkedNode* cur = _dummyHead;
        while(index--) {
            cur = cur->next;
        }
        newNode->next = cur->next;
        cur->next = newNode;
        _size++;
    }

    // 删除第index个节点，如果index 大于等于链表的长度，直接return，注意index是从0开始的
    void deleteAtIndex(int index) {
        if (index >= _size || index < 0) {
            return;
        }
        LinkedNode* cur = _dummyHead;
        while(index--) {
            cur = cur ->next;
        }
        LinkedNode* tmp = cur->next;
        cur->next = cur->next->next;
        delete tmp;
        //delete命令指示释放了tmp指针原本所指的那部分内存，
        //被delete后的指针tmp的值（地址）并非就是NULL，而是随机值。也就是被delete后，
        //如果不再加上一句tmp=nullptr,tmp会成为乱指的野指针
        //如果之后的程序不小心使用了tmp，会指向难以预想的内存空间
        tmp=nullptr;
        _size--;
    }

private:
    int _size;
    LinkedNode* _dummyHead;

};

206.反转链表

题目描述：

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：
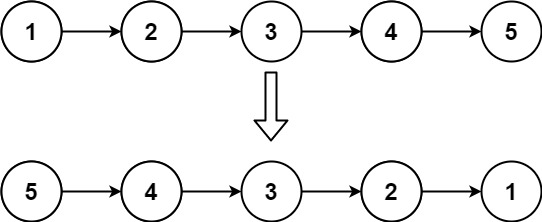
输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]
示例 2：
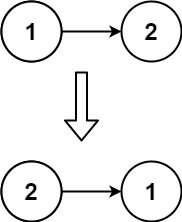
输入：head = [1,2]
输出：[2,1]
示例 3：
输入：head = []
输出：[]
提示：

链表中节点的数目范围是 [0, 5000]

-5000 <= Node.val <= 5000

进阶：链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题？

思路：

先定义一个cur指针，指向头结点，再定义一个pre指针，初始化为null。

然后就要开始反转了，首先要把 cur->next 节点用tmp指针保存一下，也就是保存一下这个节点。

为什么要保存一下这个节点呢，因为接下来要改变 cur->next 的指向了，将cur->next 指向pre ，此时已经反转了第一个节点了。

接下来，就是循环走如下代码逻辑了，继续移动pre和cur指针。

最后，cur 指针已经指向了null，循环结束，链表也反转完毕了。此时我们return pre指针就可以了，pre指针就指向了新的头结点。

法一：双指针法

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* temp; // 保存cur的下一个节点
        ListNode* cur = head;
        ListNode* pre = NULL;
        while(cur) {
            temp = cur->next;  // 保存一下 cur的下一个节点，因为接下来要改变cur->next
            cur->next = pre; // 翻转操作
            // 更新pre 和 cur指针
            pre = cur;
            cur = temp;
        }
        return pre;
    }
};

时间复杂度: O(n)
空间复杂度: O(1)

法二：递归法

递归法相对抽象一些，但是其实和双指针法是一样的逻辑，同样是当cur为空的时候循环结束，不断将cur指向pre的过程。

关键是初始化的地方，可能有的同学会不理解，可以看到双指针法中初始化cur = head，pre = NULL，在递归法中可以从如下代码看出初始化的逻辑也是一样的，只不过写法变了。

class Solution {
public:
    ListNode* reverse(ListNode* pre,ListNode* cur){
        if(cur == NULL) return pre;
        ListNode* temp = cur->next;
        cur->next = pre;
        // 可以和双指针法的代码进行对比，如下递归的写法，其实就是做了这两步
        // pre = cur;
        // cur = temp;
        return reverse(cur,temp);
    }
    ListNode* reverseList(ListNode* head) {
        // 和双指针法初始化是一样的逻辑
        // ListNode* cur = head;
        // ListNode* pre = NULL;
        return reverse(NULL, head);
    }

};

时间复杂度: O(n), 要递归处理链表的每个节点
空间复杂度: O(n), 递归调用了 n 层栈空间

我们可以发现，上面的递归写法和双指针法实质上都是从前往后翻转指针指向，其实还有另外一种与双指针法不同思路的递归写法：从后往前翻转指针指向。

法三：从后往前翻转指针指向

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        // 边缘条件判断
        if(head == NULL) return NULL;
        if (head->next == NULL) return head;
        
        // 递归调用，翻转第二个节点开始往后的链表
        ListNode *last = reverseList(head->next);
        // 翻转头节点与第二个节点的指向
        head->next->next = head;
        // 此时的 head 节点为尾节点，next 需要指向 NULL
        head->next = NULL;
        return last;
    }
};

时间复杂度: O(n)
空间复杂度: O(n)

M：24. 两两交换链表中的节点

题目描述：

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

示例 1：
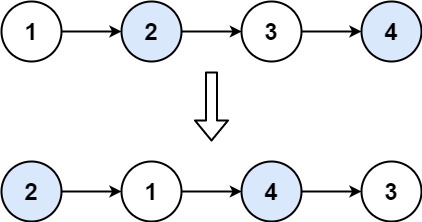
输入：head = [1,2,3,4]
输出：[2,1,4,3]
示例 2：
输入：head = []
输出：[]
示例 3：
输入：head = [1]
输出：[1]
提示：

链表中节点的数目在范围 [0, 100] 内

0 <= Node.val <= 100

思路：

这道题目正常模拟就可以了。接下来就是交换相邻两个元素了，此时一定要画图，不画图，操作多个指针很容易乱，而且要操作的先后顺序

初始时，cur指向虚拟头结点，然后进行如下三步：

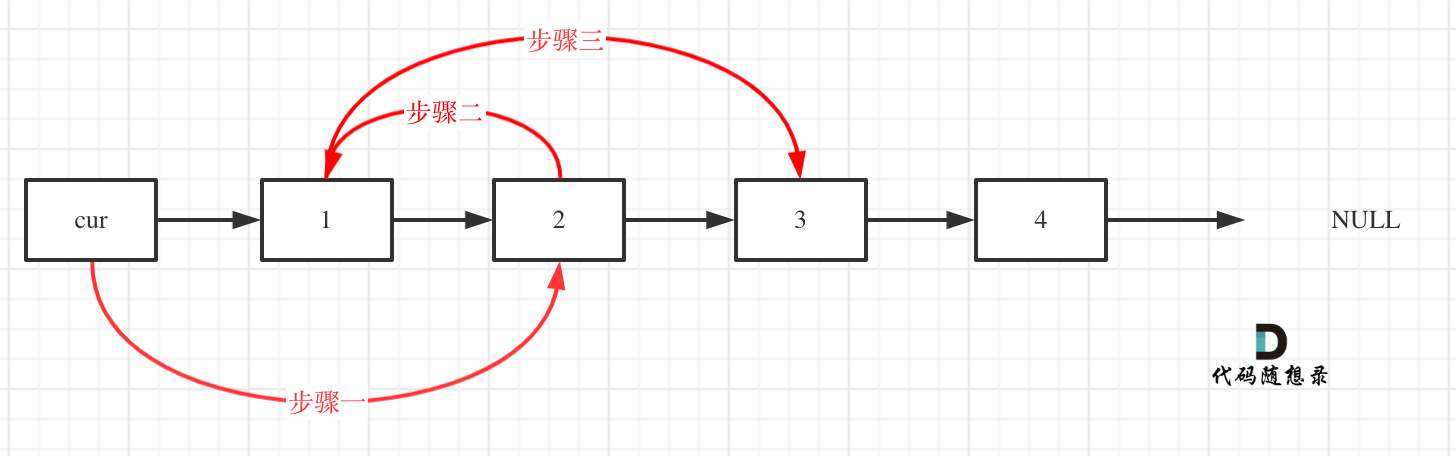
24.两两交换链表中的节点1

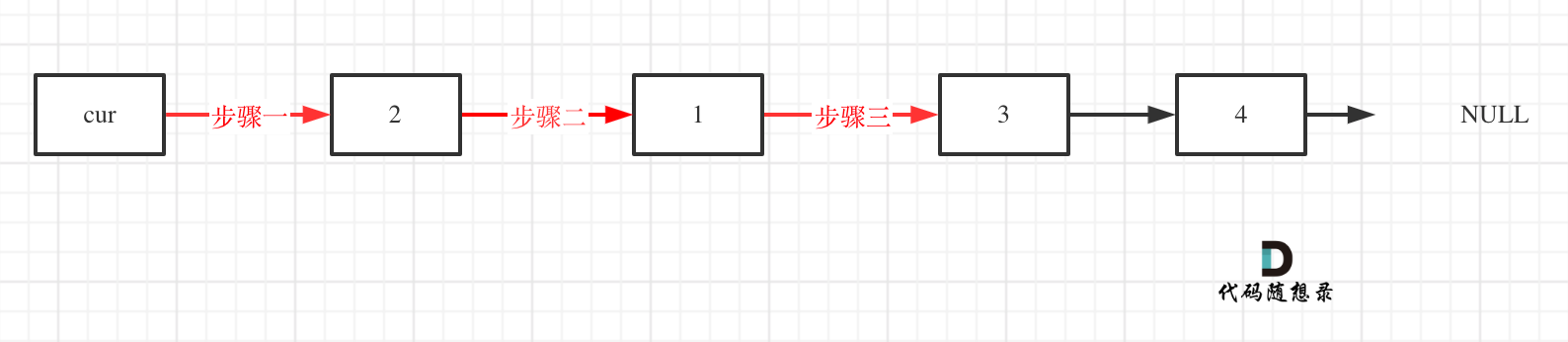
24.两两交换链表中的节点3

AC代码：

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
        dummyHead->next = head; // 将虚拟头结点指向head，这样方便后面做删除操作
        ListNode* cur = dummyHead;
        while(cur->next != nullptr && cur->next->next != nullptr) {
            ListNode* tmp = cur->next; // 记录临时节点
            ListNode* tmp1 = cur->next->next->next; // 记录临时节点

            cur->next = cur->next->next;    // 步骤一
            cur->next->next = tmp;          // 步骤二
            cur->next->next->next = tmp1;   // 步骤三

            cur = cur->next->next; // cur移动两位，准备下一轮交换
        }
        ListNode* result = dummyHead->next;
        delete dummyHead;
        return result;
    }
};

时间复杂度：O(n)
空间复杂度：O(1)

M：19.删除链表的倒数第N个节点

题目描述：

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例 1：
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]
示例 2：
输入：head = [1], n = 1
输出：[]
示例 3：
输入：head = [1,2], n = 1
输出：[1]
提示：

链表中结点的数目为 sz

1 <= sz <= 30

0 <= Node.val <= 100

1 <= n <= sz

进阶：你能尝试使用一趟扫描实现吗？

思路：双指针

双指针的经典应用，如果要删除倒数第n个节点，让fast移动n步，然后让fast和slow同时移动，直到fast指向链表末尾。删掉slow所指向的节点就可以了。

思路是这样的，但要注意一些细节。

分为如下几步：

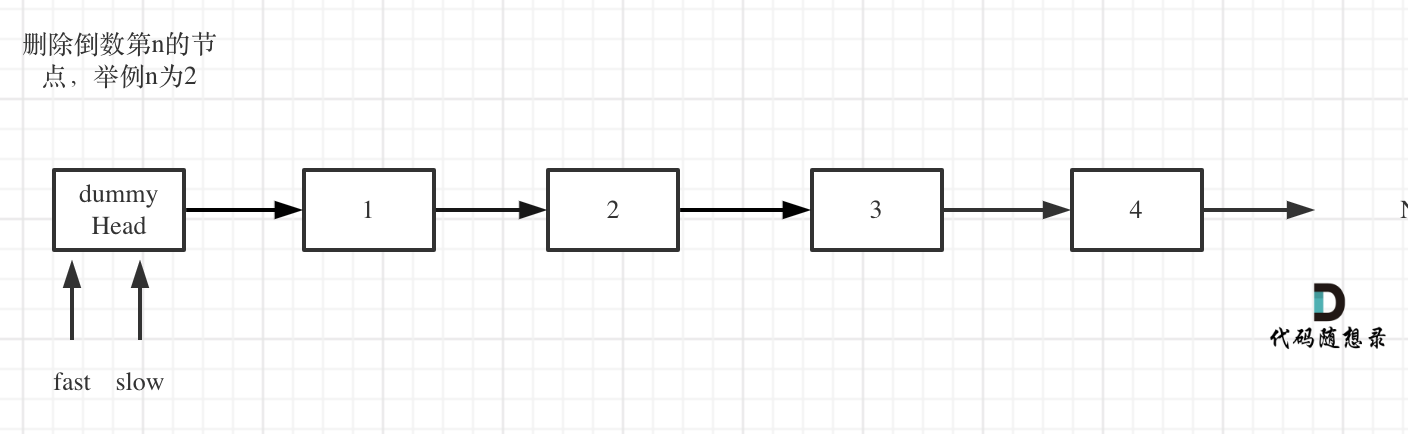
使用虚拟头结点，这样方便处理删除实际头结点的逻辑

定义fast指针和slow指针，初始值为虚拟头结点，如图：

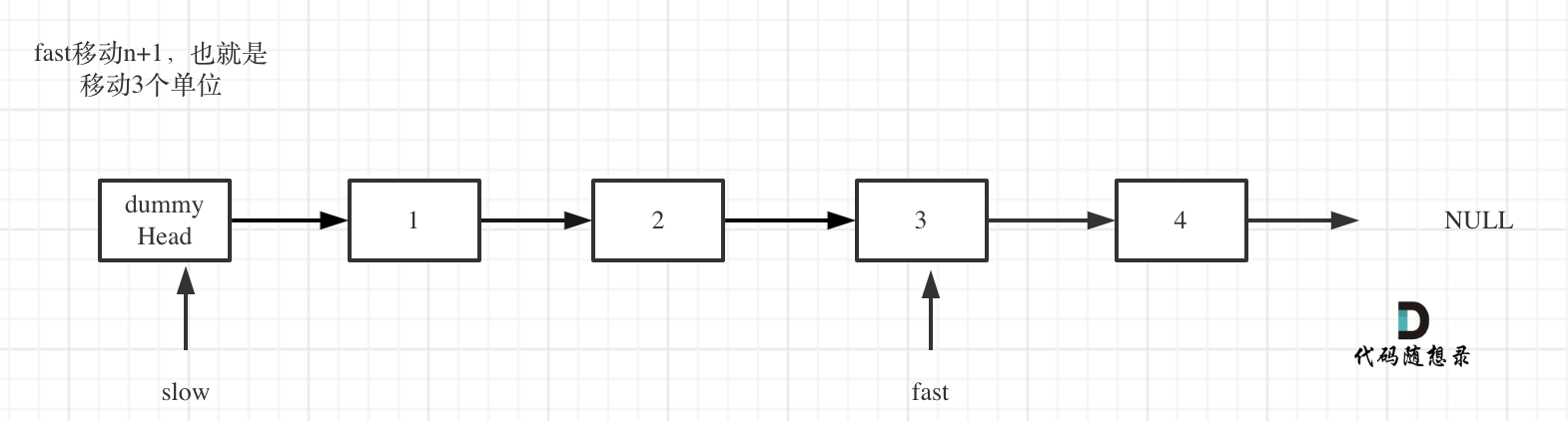
fast首先走n + 1步，为什么是n+1呢，因为只有这样同时移动的时候slow才能指向删除节点的上一个节点（方便做删除操作），如图：

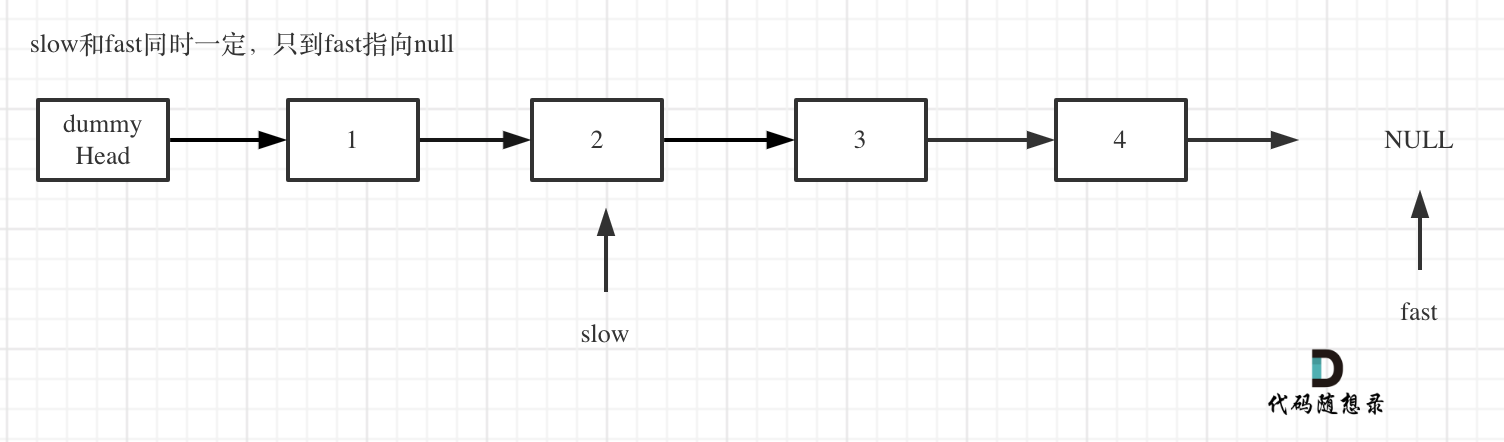
fast和slow同时移动，直到fast指向末尾，如题：

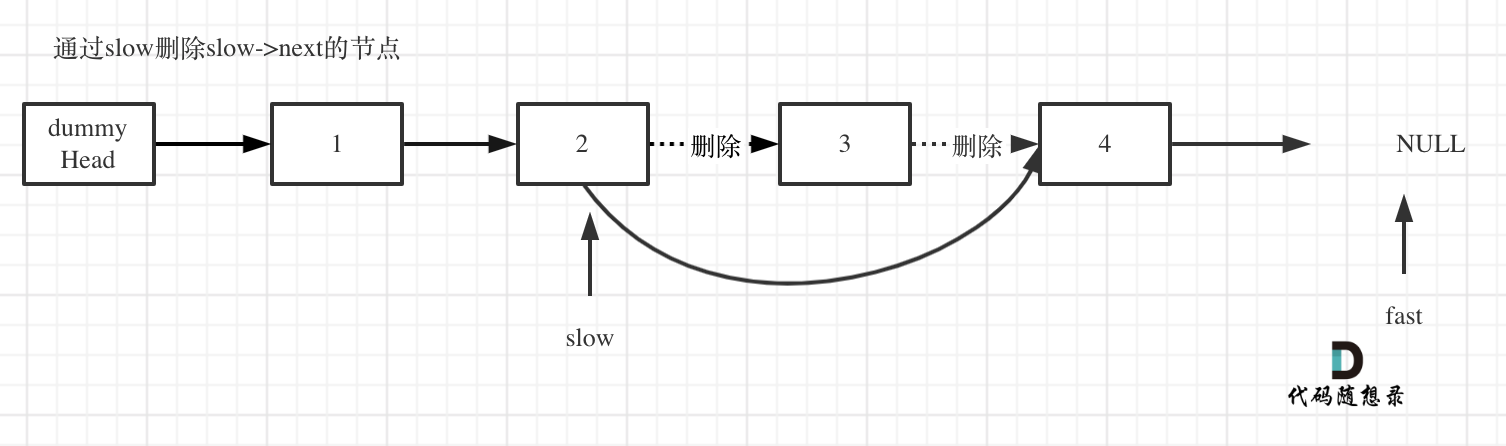
删除slow指向的下一个节点，如图：

AC代码：

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;
        ListNode* slow = dummyHead;
        ListNode* fast = dummyHead;
        while(n-- && fast != NULL) {
            fast = fast->next;
        }
        fast = fast->next; // fast再提前走一步，因为需要让slow指向删除节点的上一个节点
        while (fast != NULL) {
            fast = fast->next;
            slow = slow->next;
        }
        slow->next = slow->next->next; 
        
        // ListNode *tmp = slow->next;  C++释放内存的逻辑
        // slow->next = tmp->next;
        // delete tmp;
        
        return dummyHead->next;
    }
};

时间复杂度: O(n)
空间复杂度: O(1)

面试题 02.07. 链表相交

题意描述：

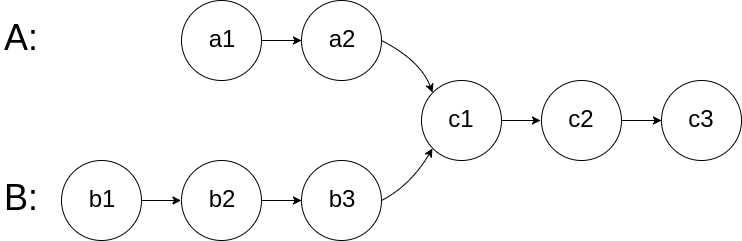
给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

图示两个链表在节点 c1 开始相交：

题目数据保证整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

示例 1：
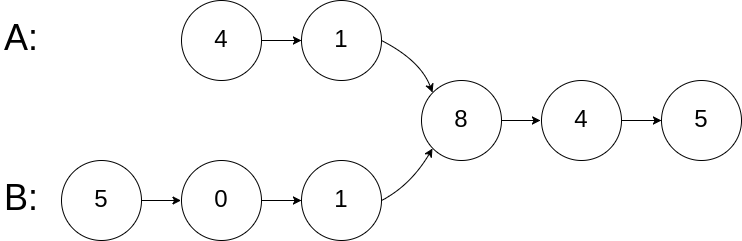
输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at '8'
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。
示例 2：
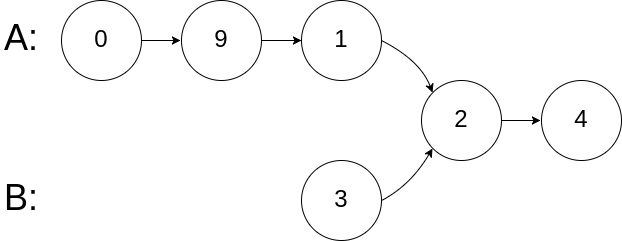
输入：intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Intersected at '2'
解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [0,9,1,2,4]，链表 B 为 [3,2,4]。
在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。
示例 3：
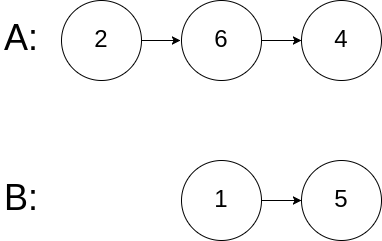
输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null
解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
这两个链表不相交，因此返回 null 。
提示：

listA 中节点数目为 m

listB 中节点数目为 n

0 <= m, n <= 3 * 104

1 <= Node.val <= 105

0 <= skipA <= m

0 <= skipB <= n

如果 listA 和 listB 没有交点，intersectVal 为 0

如果 listA 和 listB 有交点，intersectVal == listA[skipA + 1] == listB[skipB + 1]

进阶：你能否设计一个时间复杂度 O(n) 、仅用 O(1) 内存的解决方案？

思路：

简单来说，就是求两个链表交点节点的指针。这里同学们要注意，交点不是数值相等，而是指针相等。

为了方便举例，假设节点元素数值相等，则节点指针相等。

看如下两个链表，目前curA指向链表A的头结点，curB指向链表B的头结点：

我们求出两个链表的长度，并求出两个链表长度的差值，然后让curA移动到，和curB 末尾对齐的位置，如图：

此时我们就可以比较curA和curB是否相同，如果不相同，同时向后移动curA和curB，如果遇到curA == curB，则找到交点。

否则循环退出返回空指针。

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode* curA = headA;
        ListNode* curB = headB;
        int lenA = 0, lenB = 0;
        while (curA != NULL) { // 求链表A的长度
            lenA++;
            curA = curA->next;
        }
        while (curB != NULL) { // 求链表B的长度
            lenB++;
            curB = curB->next;
        }
        curA = headA;
        curB = headB;
        // 让curA为最长链表的头，lenA为其长度
        if (lenB > lenA) {
            swap (lenA, lenB);
            swap (curA, curB);
        }
        // 求长度差
        int gap = lenA - lenB;
        // 让curA和curB在同一起点上（末尾位置对齐）
        while (gap--) {
            curA = curA->next;
        }
        // 遍历curA 和 curB，遇到相同则直接返回
        while (curA != NULL) {
            if (curA == curB) {
                return curA;
            }
            curA = curA->next;
            curB = curB->next;
        }
        return NULL;
    }
};

时间复杂度：O(n + m)
空间复杂度：O(1)

M:142. 环形链表 II - 力扣（LeetCode）

题意描述：

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：
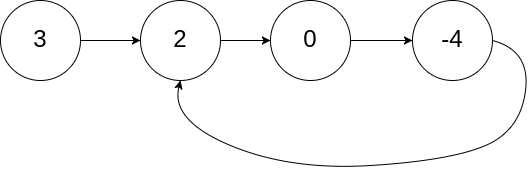
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。
示例 2：
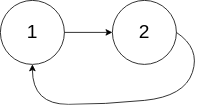
输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。
示例 3：
输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。
提示：

链表中节点的数目范围在范围 [0, 104] 内

-105 <= Node.val <= 105

pos 的值为 -1 或者链表中的一个有效索引

进阶：你是否可以使用 O(1) 空间解决此题？

思路：大体考察两知识点：

判断链表是否环
如果有环，如何找到这个环的入口

1. 判断链表是否有环

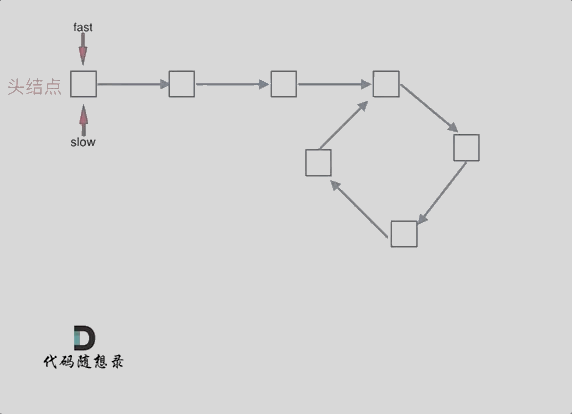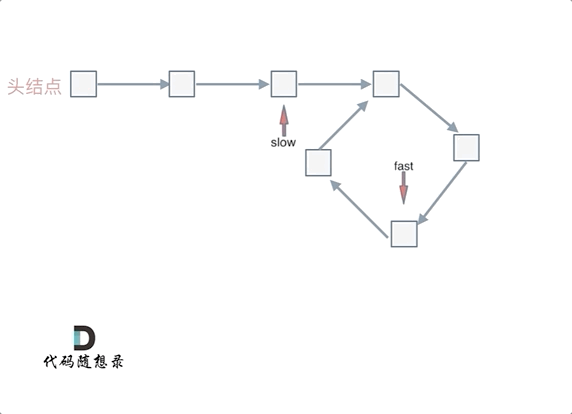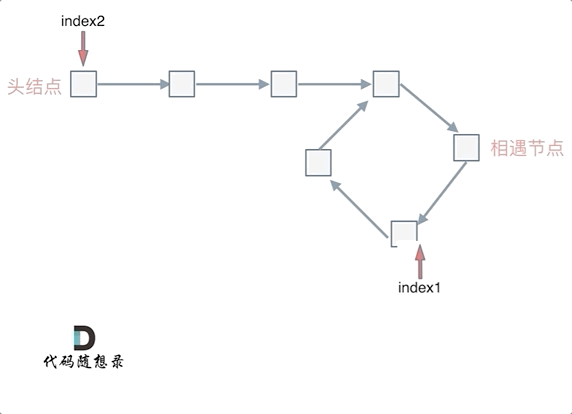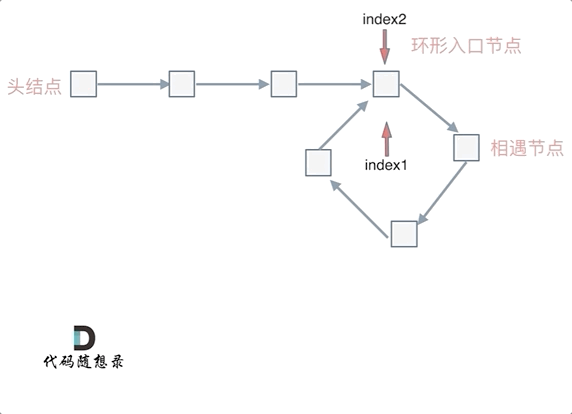
可以使用快慢指针法，分别定义 fast 和 slow 指针，从头结点出发，fast指针每次移动两个节点，slow指针每次移动一个节点，如果 fast 和 slow指针在途中相遇，说明这个链表有环。

为什么fast 走两个节点，slow走一个节点，有环的话，一定会在环内相遇呢，而不是永远的错开呢

首先第一点：fast指针一定先进入环中，如果fast指针和slow指针相遇的话，一定是在环中相遇，这是毋庸置疑的。

2.如果有环，如何找到这个环的入口

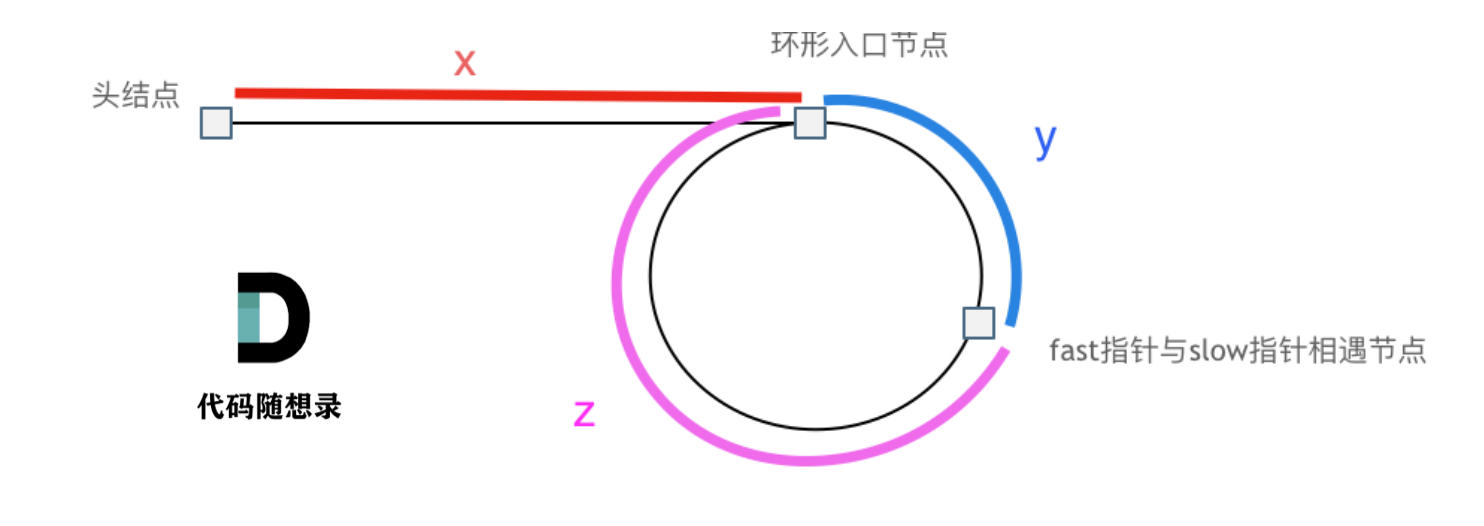
假设从头结点到环形入口节点的节点数为x。环形入口节点到fast指针与slow指针相遇节点节点数为y。从相遇节点再到环形入口节点节点数为 z。如图所示：

那么相遇时： slow指针走过的节点数为: x + y， fast指针走过的节点数：x + y + n (y + z)，n为fast指针在环内走了n圈才遇到slow指针，（y+z）为一圈内节点的个数A。

因为fast指针是一步走两个节点，slow指针一步走一个节点，所以 fast指针走过的节点数 = slow指针走过的节点数 * 2：
(x + y) * 2 = x + y + n (y + z)
两边消掉一个（x+y）: x + y = n (y + z)

因为要找环形的入口，那么要求的是x，因为x表示头结点到环形入口节点的的距离。

所以要求x ，将x单独放在左面：x = n (y + z) - y ,

再从n(y+z)中提出一个（y+z）来，整理公式之后为如下公式：x = (n - 1) (y + z) + z 注意这里n一定是大于等于1的，因为 fast指针至少要多走一圈才能相遇slow指针。

这个公式说明什么呢？

先拿n为1的情况来举例，意味着fast指针在环形里转了一圈之后，就遇到了 slow指针了。

当 n为1的时候，公式就化解为 x = z，

这就意味着，从头结点出发一个指针，从相遇节点也出发一个指针，这两个指针每次只走一个节点，那么当这两个指针相遇的时候就是环形入口的节点。

也就是在相遇节点处，定义一个指针index1，在头结点处定一个指针index2。

让index1和index2同时移动，每次移动一个节点，那么他们相遇的地方就是环形入口的节点。

n大于1,就是fast指针在环形转n圈之后才遇到 slow指针。

其实这种情况和n为1的时候效果是一样的，一样可以通过这个方法找到环形的入口节点，只不过，index1 指针在环里多转了(n-1)圈，然后再遇到index2，相遇点依然是环形的入口节点。

AC代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while(fast != NULL && fast->next != NULL) {
            slow = slow->next;
            fast = fast->next->next;
            // 快慢指针相遇，此时从head 和 相遇点，同时查找直至相遇
            if (slow == fast) {
                ListNode* index1 = fast;
                ListNode* index2 = head;
                while (index1 != index2) {
                    index1 = index1->next;
                    index2 = index2->next;
                }
                return index2; // 返回环的入口
            }
        }
        return NULL;
    }
};

时间复杂度: O(n)，快慢指针相遇前，指针走的次数小于链表长度，快慢指针相遇后，两个index指针走的次数也小于链表长度，总体为走的次数小于 2n
空间复杂度: O(1)

234. 回文链表

题目描述：

给你一个单链表的头节点 head ，请你判断该链表是否为回文链表

。如果是，返回 true ；否则，返回 false 。

示例 1：
输入：head = [1,2,2,1]
输出：true
示例 2：
输入：head = [1,2]
输出：false
提示：

链表中节点数目在范围[1, 105] 内

0 <= Node.val <= 9

进阶：你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题？

思路1：数组模拟

最直接的想法，就是把链表装成数组，然后再判断是否回文。

代码也比较简单。如下：

class Solution {
public:
    bool isPalindrome(ListNode* head) {
        vector<int> vec;
        ListNode* cur  = head;
        while (cur) {
            vec.push_back(cur->val);
            cur = cur->next;
        }
        // 比较数组回文
        for (int i = 0, j = vec.size() - 1; i < j; i++, j--) {
            if (vec[i] != vec[j]) return false;
        }
        return true;
    }
};

上面代码可以在优化，就是先求出链表长度，然后给定vector的初始长度，这样避免vector每次添加节点重新开辟空间

class Solution {
public:
    bool isPalindrome(ListNode* head) {

        ListNode* cur  = head;
        int length = 0;
        while (cur) {
            length++;
            cur = cur->next;
        }
        vector<int> vec(length, 0); // 给定vector的初始长度，这样避免vector每次添加节点重新开辟空间
        cur = head;
        int index = 0;
        while (cur) {
            vec[index++] = cur->val;
            cur = cur->next;
        }
        // 比较数组回文
        for (int i = 0, j = vec.size() - 1; i < j; i++, j--) {
            if (vec[i] != vec[j]) return false;
        }
        return true;
    }
};

思路2：反转后半部分链表

分为如下几步：

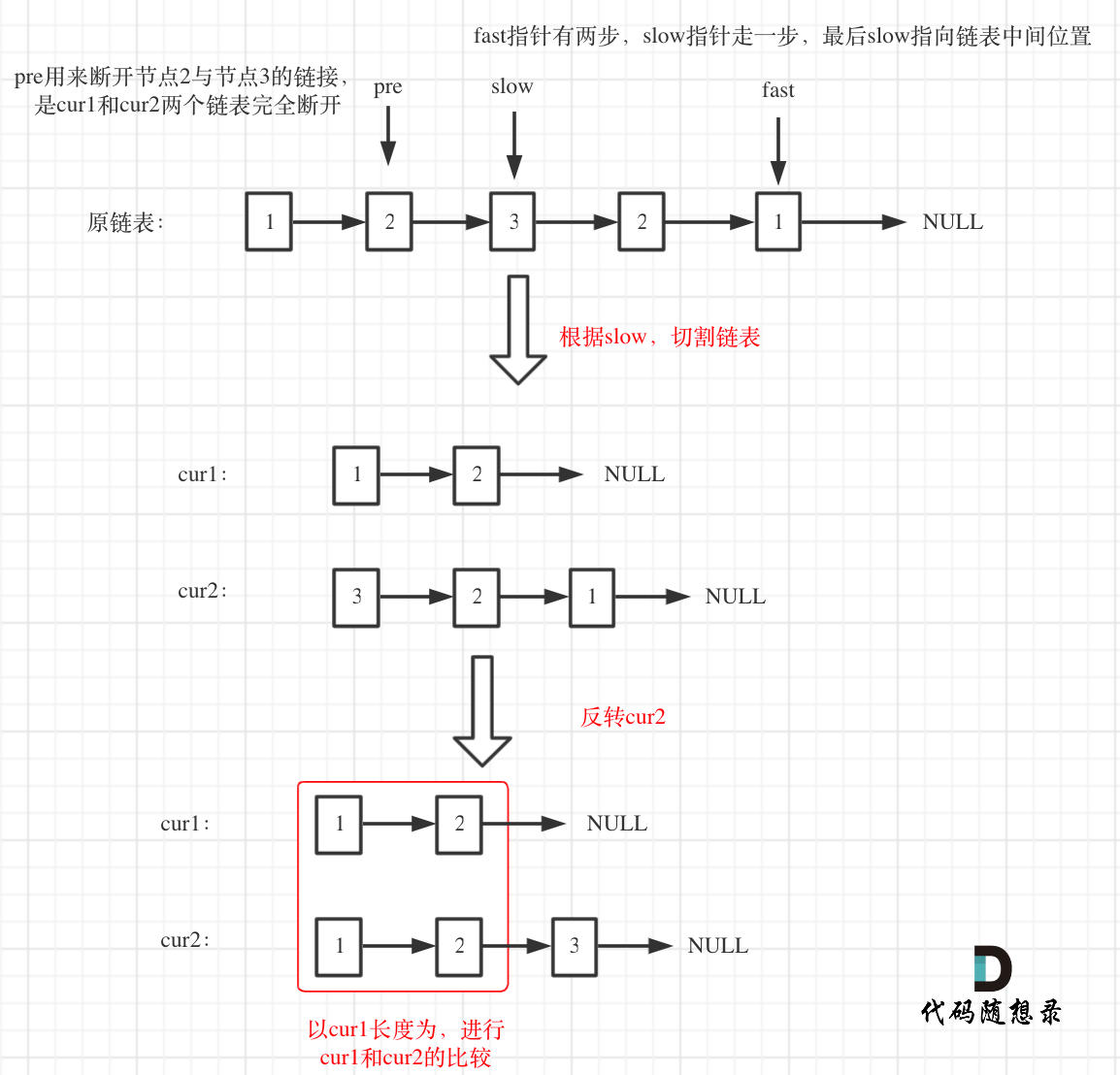
用快慢指针，快指针有两步，慢指针走一步，快指针遇到终止位置时，慢指针就在链表中间位置

同时用pre记录慢指针指向节点的前一个节点，用来分割链表

将链表分为前后均等两部分，如果链表长度是奇数，那么后半部分多一个节点

将后半部分反转，得cur2，前半部分为cur1

按照cur1的长度，一次比较cur1和cur2的节点数值

如图所示：

代码如下：

class Solution {
public:
    bool isPalindrome(ListNode* head) {
        if (head == nullptr || head->next == nullptr) return true;
        ListNode* slow = head; // 慢指针，找到链表中间分位置，作为分割
        ListNode* fast = head;
        ListNode* pre = head; // 记录慢指针的前一个节点，用来分割链表
        while (fast && fast->next) {
            pre = slow;
            slow = slow->next;
            fast = fast->next->next;
        }
        pre->next = nullptr; // 分割链表

        ListNode* cur1 = head;  // 前半部分
        ListNode* cur2 = reverseList(slow); // 反转后半部分，总链表长度如果是奇数，cur2比cur1多一个节点

        // 开始两个链表的比较
        while (cur1) {
            if (cur1->val != cur2->val) return false;
            cur1 = cur1->next;
            cur2 = cur2->next;
        }
        return true;
    }
    // 反转链表
    ListNode* reverseList(ListNode* head) {
        ListNode* temp; // 保存cur的下一个节点
        ListNode* cur = head;
        ListNode* pre = nullptr;
        while(cur) {
            temp = cur->next;  // 保存一下 cur的下一个节点，因为接下来要改变cur->next
            cur->next = pre; // 翻转操作
            // 更新pre 和 cur指针
            pre = cur;
            cur = temp;
        }
        return pre;
    }
};

143.重排链表

题目描述：

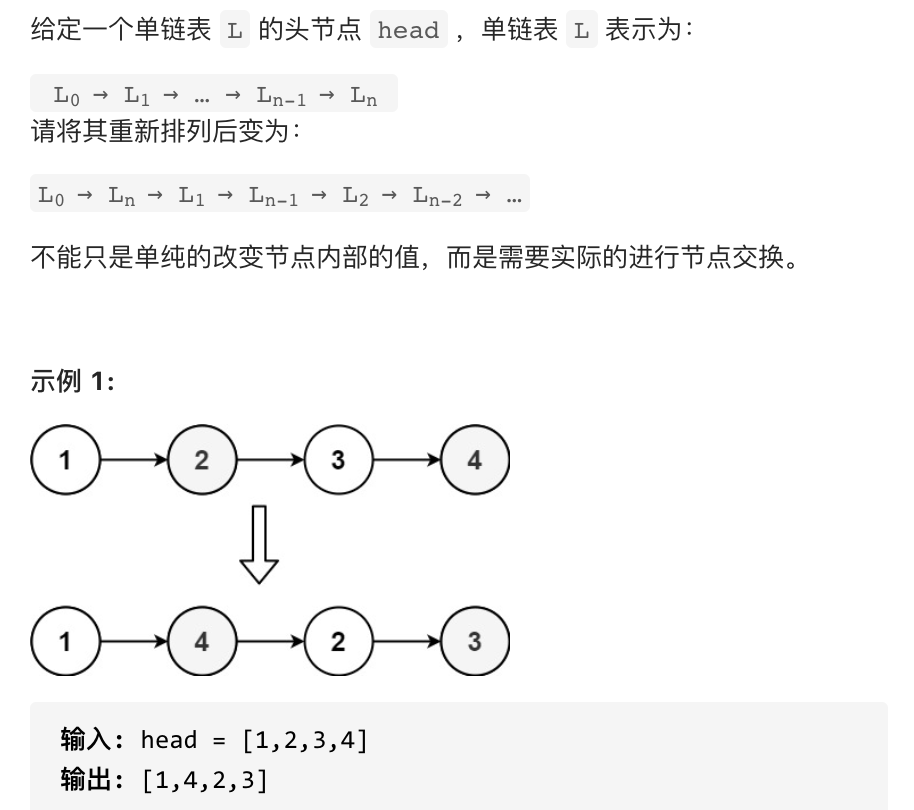
思路：

数组模拟
双向队列模拟
直接分割链表

方法一：数组模拟

把链表放进数组中，然后通过双指针法，一前一后，来遍历数组，构造链表。

代码如下：

class Solution {
public:
    void reorderList(ListNode* head) {
        vector<ListNode*> vec;
        ListNode* cur = head;
        if (cur == nullptr) return;
        while(cur != nullptr) {
            vec.push_back(cur);
            cur = cur->next;
        }
        cur = head;
        int i = 1;
        int j = vec.size() - 1;  // i j为之前前后的双指针
        int count = 0; // 计数，偶数去后面，奇数取前面
        while (i <= j) {
            if (count % 2 == 0) {
                cur->next = vec[j];
                j--;
            } else {
                cur->next = vec[i];
                i++;
            }
            cur = cur->next;
            count++;
        }
        cur->next = nullptr; // 注意结尾
    }
};

方法二：双向队列模拟

把链表放进双向队列，然后通过双向队列一前一后弹出数据，来构造新的链表。这种方法比操作数组容易一些，不用双指针模拟一前一后了。

class Solution {
public:
    void reorderList(ListNode* head) {
        deque<ListNode*> que;
        ListNode* cur = head;
        if (cur == nullptr) return;

        while(cur->next != nullptr) {
            que.push_back(cur->next);
            cur = cur->next;
        }

        cur = head;
        int count = 0; // 计数，偶数去后面，奇数取前面
        ListNode* node;
        while(que.size()) {
            if (count % 2 == 0) {
                node = que.back();
                que.pop_back();
            } else {
                node = que.front();
                que.pop_front();
            }
            count++;
            cur->next = node;
            cur = cur->next;
        }
        cur->next = nullptr; // 注意结尾
    }
};

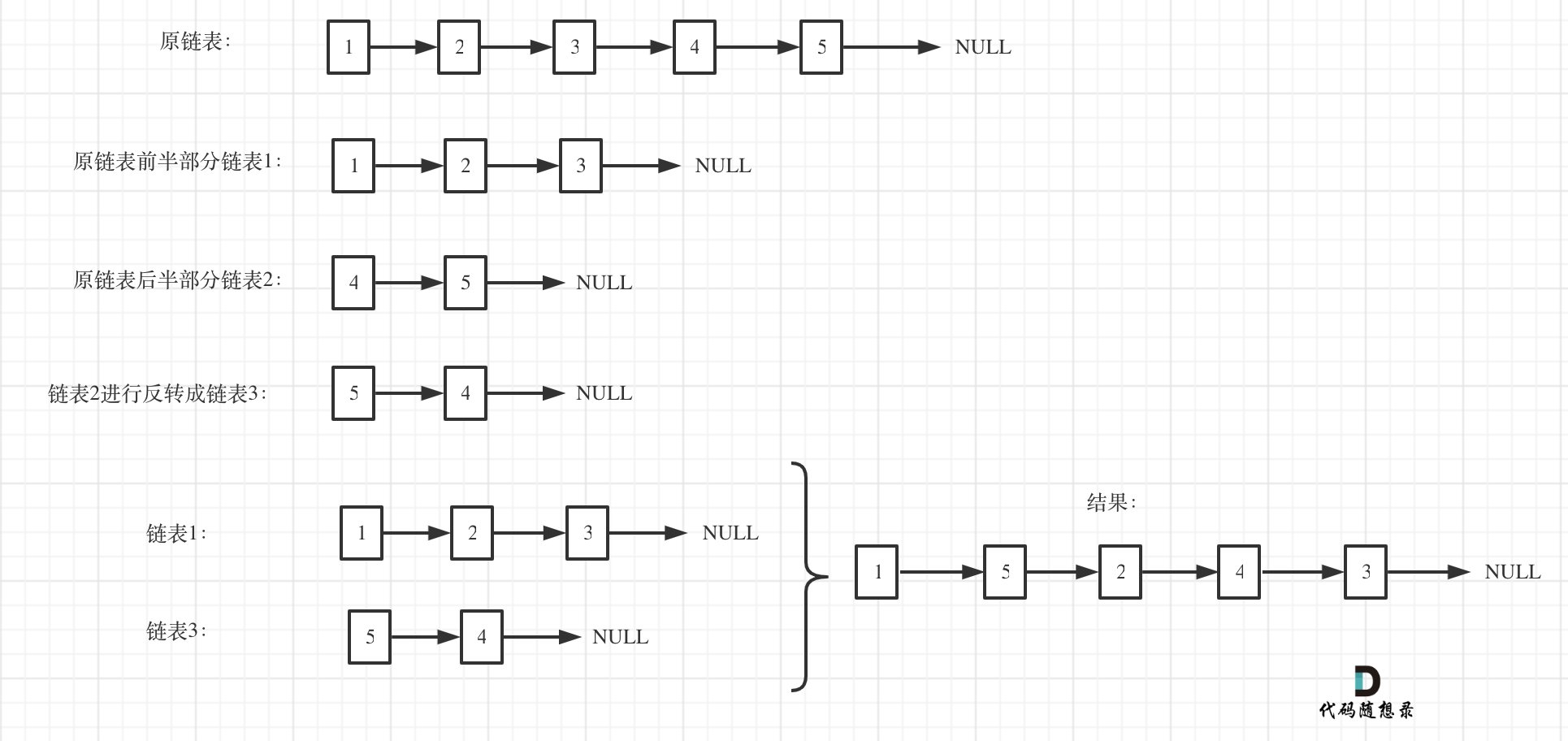
方法三：直接分割链表

将链表分割成两个链表，然后把第二个链表反转，之后在通过两个链表拼接成新的链表。

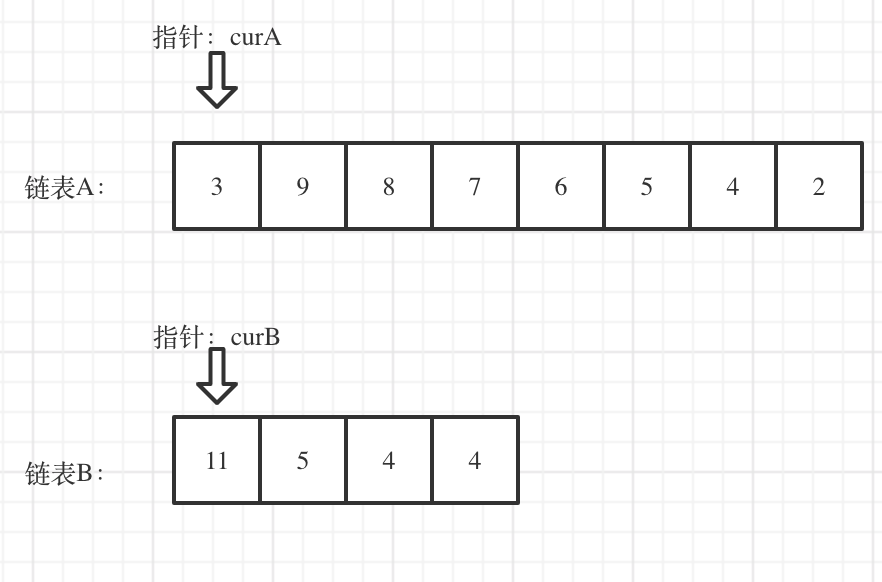
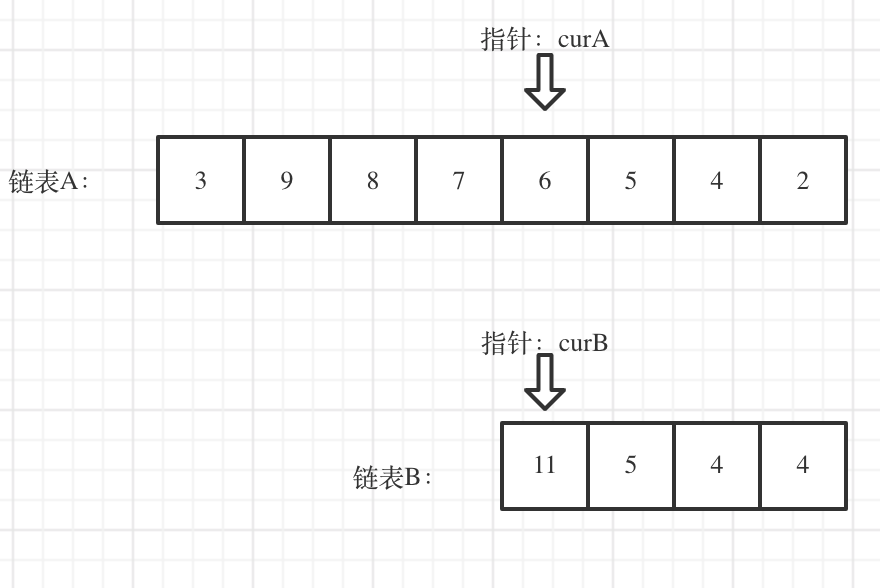
如图：

这种方法，比较难，平均切割链表，看上去很简单，真正代码写的时候有很多细节，同时两个链表最后拼装整一个新的链表也有一些细节需要注意！

代码如下：

class Solution {
private:
    // 反转链表
    ListNode* reverseList(ListNode* head) {
        ListNode* temp; // 保存cur的下一个节点
        ListNode* cur = head;
        ListNode* pre = NULL;
        while(cur) {
            temp = cur->next;  // 保存一下 cur的下一个节点，因为接下来要改变cur->next
            cur->next = pre; // 翻转操作
            // 更新pre 和 cur指针
            pre = cur;
            cur = temp;
        }
        return pre;
    }

public:
    void reorderList(ListNode* head) {
        if (head == nullptr) return;
        // 使用快慢指针法，将链表分成长度均等的两个链表head1和head2
        // 如果总链表长度为奇数，则head1相对head2多一个节点
        ListNode* fast = head;
        ListNode* slow = head;
        while (fast && fast->next && fast->next->next) {
            fast = fast->next->next;
            slow = slow->next;
        }
        ListNode* head1 = head;
        ListNode* head2;
        head2 = slow->next;
        slow->next = nullptr;

        // 对head2进行翻转
        head2 = reverseList(head2);

        // 将head1和head2交替生成新的链表head
        ListNode* cur1 = head1;
        ListNode* cur2 = head2;
        ListNode* cur = head;
        cur1 = cur1->next;
        int count = 0; // 偶数取head2的元素，奇数取head1的元素
        while (cur1 && cur2) {
            if (count % 2 == 0) {
                cur->next = cur2;
                cur2 = cur2->next;
            } else {
                cur->next = cur1;
                cur1 = cur1->next;
            }
            count++;
            cur = cur->next;
        }
        if (cur2 != nullptr) { // 处理结尾
            cur->next = cur2;
        }
        if (cur1 != nullptr) {
            cur->next = cur1;
        }
    }
};

标签：head,ListNode,cur,--,next,链表,6.6,节点
From： https://www.cnblogs.com/7dragonpig/p/18236073

链表的定义

链表的操作链表的操作

题目描述：

思路：设置虚拟头结点：以一种统一的逻辑来移除链表的节点

AC代码：

题目描述：

思路：

AC代码：

题目描述：

思路：

法一：双指针法

法二：递归法

法三：从后往前翻转指针指向

题目描述：

思路：

AC代码：

题目描述：

思路：双指针

AC代码：

题意描述：

思路：

题意描述：

思路：大体考察两知识点：

1. 判断链表是否有环

2.如果有环，如何找到这个环的入口

AC代码：

题目描述：

思路1：数组模拟

思路2：反转后半部分链表

题目描述：

思路：

方法一：数组模拟

方法二：双向队列模拟

方法三：直接分割链表

相关文章

赞助商

阅读排行