[JSOI2015] 染色问题

题目描述

萌萌家有一个棋盘，这个棋盘是一个 \(n \times m\) 的矩形，分成 \(n\) 行 \(m\) 列共 \(n \times m\) 个小方格。
现在萌萌和南南有 \(C\) 种不同颜色的颜料，他们希望把棋盘用这些颜料染色，并满足以下规定：

1. 棋盘的每一个小方格既可以染色（染成 \(C\) 种颜色中的一种），也可以不染色。
2. 棋盘的每一行至少有一个小方格被染色。
3. 棋盘的每一列至少有一个小方格被染色。
4. 每种颜色都在棋盘上出现至少一次。

以下是一些将 \(3 \times 3\) 棋盘染成 \(C=3\) 种颜色（红、黄、蓝）的例子（下图已更新）：

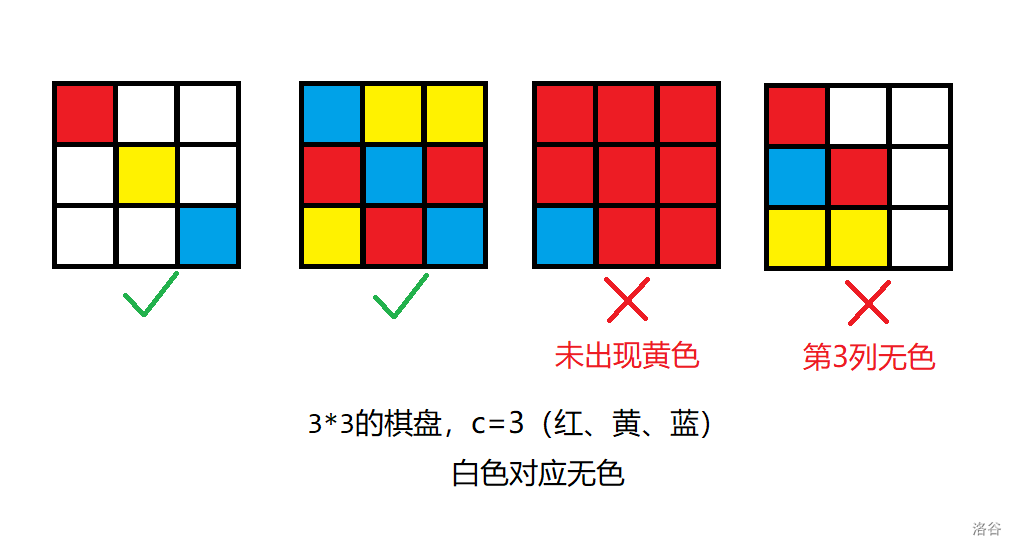
请你求出满足要求的不同的染色方案总数。只要存在一个位置的颜色不同，即认为两个染色方案是不同的。

输入格式

输入只有一行，为 \(3\) 个整数 \(n,m,c\)。

输出格式

输出一个整数，为不同染色方案总数。
因为总数可能很大，只需输出总数对 \(1,000,000,007\) 取模的值。

样例 #1

样例输入 #1

2 2 3

样例输出 #1

60

提示

对于\(100\%\)的数据，\(1 \le n,m,c \le 400\)。