BFS

在最优性问题中，状态按照非最优化属性进行分组，且每个分组存在且只需要保留最优状态。

一般最优性问题分为 \(2\) 种，边权为正数、边权为非负数。

边权为正数且相同

这种情况，转移时最优化属性的值会变得更劣，每次转移时最优化属性的值会变劣最小单位。

而最优化属性有拓扑序，可以按照拓扑序进行搜索，由优到劣对每层的状态进行搜索。在这种问题中每个分组中首次被搜到的状态就是最优的，之后的同组状态都可以忽略不计，可以用 BFS 逐层对状态进行处理，如图：

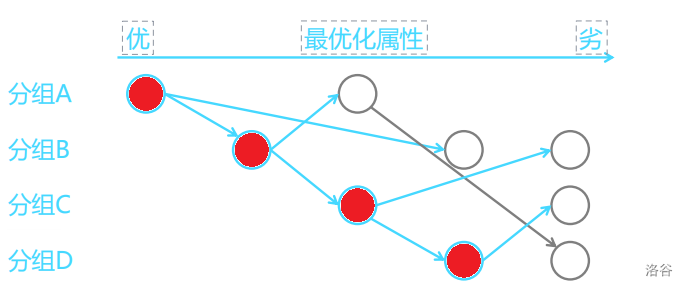
标红的点即为每个分组的最优状态，可用队列实现。

边权为非负数

转移时最优化属性的值不会变得更优。

这种情况是在上一种情况上增添了同一层连边的情况，发先这时没有拓扑序。

这时我们可以改动 BFS，先将同层的转移处理完，在处理后面层的转移，同样，每个分组中首次被处理的状态就是最优的，之后的同组状态都可以忽略。

如果拓展出同层状态就插入队头，否则插到队尾，所以我们需要一个双端队列。

边权为非负数但不同

记边权值域为 \(V\)，那么我们可以开 \(V\) 个队列用并查集维护第一个不为空的队列进行拓展，发现这东西就是最短路，而用并查集维护其实就是堆找最小值，这种方法时间复杂度跟 Dij 没有太大差距，但空间巨大。

upd：并查集路压缩径加按秩合并后复杂度好似更优。

写法

• BFS有两种写法：

  1.每产生一个状态就将它加入队列，在处理状态时判断是否可能是最优的。

  2.每产生一个状态先判断是否可能是最优的，再加入队列。

第一种方法适用面更广，但时间复杂度会更高，有些题用第二种方法会简便些，但有些题只能用第一种方法。

题目

P1443 马的遍历

首先先确定状态，\((x,y,t)\) 为走到格子 \(x,y\) 的时间为 \(t\)，发现最优化属性为 \(t\)，所以根据非最优化属性进行分组，将 \(x,y\) 相同的状态分为一组，其移动为转移，即为变劣最小单位，可用广搜实现。

第二种写法标准代码：

# include <bits/stdc++.h>

using namespace std;

const int N = 405;
const int kD[][2] = {{-1, -2}, {-1, 2}, {1, -2}, {1, 2}, {-2, -1}, {-2, 1}, {2, -1}, {2, 1}};  

struct node {
  int x, y;
} q[N * N]; 

int d[N][N], n, m, x, y, h = 1, t;  

void Record (int x, int y, int v) {//广搜习惯在这里写一个Record函数来处理新状态                  
  if (x < 1 || x > n || y < 1 || y > m || d[x][y]) { 
    return;                                          
  }
  d[x][y] = v;   
  q[++ t] = {x, y};  
}

int main() {
  cin >> n >> m >> x >> y;
  for (Record(x, y, 1); h <= t; h ++) {                                     
    for (int i = 0; i < 8; i ++) {                                          
      Record(q[h].x + kD[i][0], q[h].y + kD[i][1], d[q[h].x][q[h].y] + 1);  
    }
  }
  for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= m; j++) {
      cout << setw(5) << d[i][j] - 1;
    }
    cout << "\n";
  }
  return 0;
}