\(\color{purple}(1)\) CF746G New Roads
- 构造一棵 \(n\) 个点的深度为 \(t\) 的树,以 \(1\) 为根,使其中深度为 \(i\) 的点有 \(a_i\) 个且叶节点有 \(k\) 个。或报告无解。
- \(t, k \le n \le 2 \times 10^5\)。
为了方便,我们令根节点的深度为 \(1\)。所有读入都向后顺延一位。
首先计算这棵树最多和最少有几个叶子节点,那么如果 \(k\) 不在这个范围内则无解。那么模拟样例二:
第一个观察是无论如何构造,最后一层的节点一定是叶子节点,且第一层一定不是叶节点。
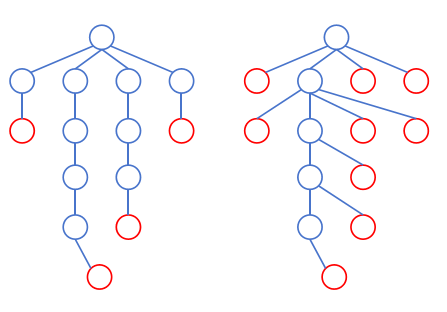
可以发现叶子最多的情况,是每一层的节点都连向上一层的同一个节点,即 \(k_{\max} = a_t + \sum_{i=1}^{t-1}\max(a_i - a_{i + 1}, 0)\)。叶子最少的情况,是每一层的节点都尽可能f多的连向上一层的不同的点,直到不能连为止,即 \(k_{\min} = a_t + \sum_{i=1}^{t-1} (a_i - 1)\)。
除第一层外和最后一层外,每一层的叶子节点数一定不会少于 \(a_i - a_{i + 1}\)(如左图)且不会超过 \(a_i - 1\)(如右图)。那么我们可以处理出 \(b_2, b_3, \dots, b_{t - 1}\) 表示我们将要在第 \(i\) 层构造出 \(b_i\) 个叶子节点。需要保证 \(\max(0, a_i - a_{i + 1}) \le b_i \le a_i - 1\) 且 \(\sum_{i=2}^{t-1} b_i = k - a_t\)。这是极易做到的。
然后考虑根据 \(b\) 数组构造整棵树。显然我们需要满足第 \(i\) 层中有 \(a_i - b_i\) 个点不是叶子节点,即连接至少一个下一层的点。那么直接模拟构造即可。
$\color{blue}\text{Code}$
int n, k, t, a[N], sum[N];
int Id(int a, int b) { // 第 a 层的第 b 个点
return sum[a - 1] + b;
}
int mn() {
int res = a[t];
for (int i = 1; i < t; ++ i )
if (a[i] > a[i + 1]) res += a[i] - a[i + 1];
return res;
}
int mx() {
int res = a[t];
for (int i = 1; i < t; ++ i )
res += a[i] - 1;
return res;
}
int b[N];
vector<pair<int, int> > res;
void build_b() {
int lst = k - a[t];
for (int i = 2; i < t; ++ i ) {
b[i] = max(0ll, a[i] - a[i + 1]);
lst -= b[i];
}
for (int i = 2; i < t; ++ i ) {
int tmp = min(lst, a[i] - 1 - b[i]);
b[i] += tmp;
lst -= tmp;
}
}
void Luogu_UID_748509() {
fin >> n >> t >> k;
++ t;
sum[1] = 1;
a[1] = 1;
for (int i = 2; i <= t; ++ i ) fin >> a[i], sum[i] = sum[i - 1] + a[i];
if (k < mn() || k > mx()) puts("-1");
else {
build_b();
for (int i = 1; i < t; ++ i ) {
int x = a[i] - b[i];
for (int j = 1; j <= x; ++ j )
res.emplace_back(Id(i, j), Id(i + 1, j));
for (int j = x + 1; j <= a[i + 1]; ++ j )
res.emplace_back(Id(i, x), Id(i + 1, j));
}
fout << n << '\n';
for (auto t : res) fout << t.first << ' ' << t.second << '\n';
}
}