给你一棵二叉树的根节点 root ,二叉树中节点的值 互不相同 。另给你一个整数 start 。在第 0 分钟,感染 将会从值为 start 的节点开始爆发。
每分钟,如果节点满足以下全部条件,就会被感染:
- 节点此前还没有感染。
- 节点与一个已感染节点相邻。
返回感染整棵树需要的分钟数。
示例 1:
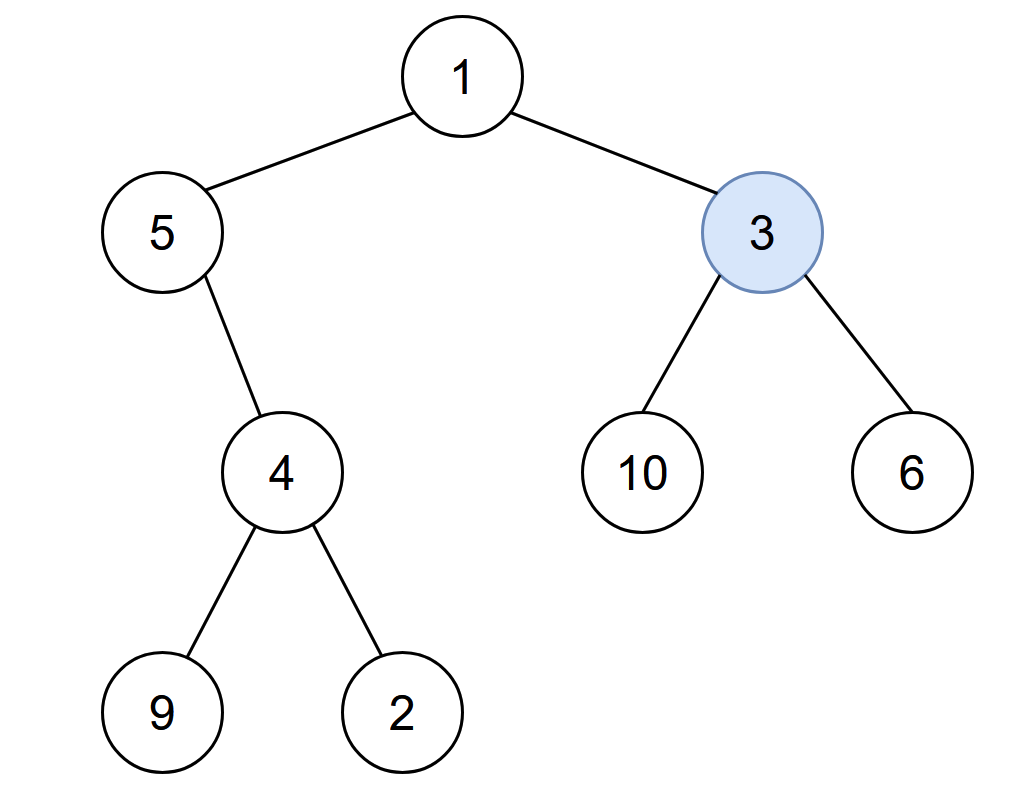
输入:root = [1,5,3,null,4,10,6,9,2], start = 3
输出:4
解释:节点按以下过程被感染:
- 第 0 分钟:节点 3
- 第 1 分钟:节点 1、10、6
- 第 2 分钟:节点5
- 第 3 分钟:节点 4
- 第 4 分钟:节点 9 和 2
感染整棵树需要 4 分钟,所以返回 4 。示例 2:

输入:root = [1], start = 1
输出:0
解释:第 0 分钟,树中唯一一个节点处于感染状态,返回 0 。提示:
- 树中节点的数目在范围
[1, 105]内 1 <= Node.val <= 105- 每个节点的值 互不相同
- 树中必定存在值为
start的节点
这道题本质上就是求start节点到树中其他节点的最远距离,本来的想法是最远节点要么是start节点继续向下走,走到的最深节点;要么是start节点往上走,某处拐弯后再到另一边子树的最深节点。据说这叫求二叉树的直径。
但是start这里给出的只不过是一个值而已,所以要找到start节点在树中的位置就得花一番工夫,包括找到“拐弯”总觉得有点麻烦。
常规解法还是先将树的结构用深度优先搜索解析成无向图,再用广度优先搜索来求最长距离。代码中graph为邻接表,用一个哈希表来表示,哈希表的键为节点值,值为其相邻节点的值组成的列表。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def amountOfTime(self, root, start):
"""
:type root: Optional[TreeNode]
:type start: int
:rtype: int
"""
# 本质上就是计算start节点到其他节点的最远距离
# 用dfs把树的结构解析成无向图,用邻接表存储
graph = defaultdict(list)
def dfs(node):
for child in [node.left, node.right]:
if child:
graph[node.val].append(child.val)
graph[child.val].append(node.val)
dfs(child)
dfs(root)
# 用bfs求最长距离
q = deque([(start, 0)]) # (node, infection time)
visited = set([start])
time = 0
while q:
nodeVal, time = q.popleft()
for childVal in graph[nodeVal]:
if childVal not in visited:
q.append([childVal, time+1])
visited.add(childVal)
return time复杂度分析
-
时间复杂度:O(n)O(n)O(n),其中 nnn 是树的节点个数。
-
空间复杂度:O(n)O(n)O(n)。