网络流的建图灵活,需要大量练习。
一些常见套路:
-
拆点:一般来说可以把一个点拆为一个入点和一个出点并连边,用于点边转化。
-
连 INF 边:这种边不可能包含在最小割中,可以用来将点定向。
-
建立超级源点和超级汇点:用于构建网络流模型。
-
加辅助点:比较灵活,可以用于处理多种问题。
做题记录:
1.P1345 [USACO5.4] 奶牛的电信Telecowmunication
比较经典的一道拆点题。
具体做法就是将每个点拆为一个入点和一个出点并连上容量为一的边,并将题目中给出的边全部设为 INF, 那么问题转化为了最小割。
直接做 \(\rm dinic\) 求网络流即可。
2.P2057 [SHOI2007] 善意的投票 / [JLOI2010] 冠军调查
一道经典的二者选其一的题目。
把小朋友看作点,我们发现题目实际上是要把所有点分为两个点集,这很像最小割模型。
先建一个超级源点 \(s\) 和一个超级汇点 \(t\),如果一个点分到 \(S\) 点集就表示同意睡觉,分到 \(T\) 就是不同意。
考虑如何表示出意愿对答案的贡献,容易想出如果同意就跟 \(s\) 连边,否则与 \(t\) 连边,容量为 1。
接下来考虑小朋友之间的关系对答案的贡献,很显然的,将小朋友连上双向边即可(容量为 1)。
3.P1361 小M的作物
正面不好做,正难则反。先将原题的所有给出的可能贡献值加起来,现在问题转化为最小化减掉的贡献。
还是二者选其一问题,对于第一类贡献,像上一题一样套路的建源汇点,并连边,容量为贡献值。
对于第二类贡献,直接连边显然不可行。于是考虑加入辅助点,我们简化到两点的情况:(学校不好画图就借鉴题解的了)
此时我们加入两个辅助点,类似于这样:
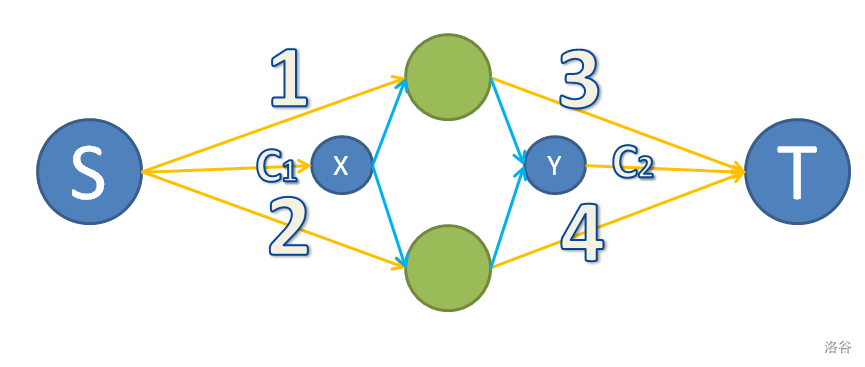
黄边的容量和方向比较好想,关键是蓝边的容量和方向。
我们分类讨论两点的选择情况:
1.两点都在 \(S\) 集合中,我们要强迫点 \(S\) 在 \(S\) 集合中,于是我们从两点向 \(Y\) 连边,容量为 INF,此时 \(Y\) 与 \(T\) 的边会计算到割中,而两条容量 INF 的边变为了反向边,不会记录到割中。
2.两者都在 \(T\) 集合中,同理连边。
3.两者不同集合。此时的图已经完美的符合了这个情况,可以自己手推一下。
4.P2857 [USACO06FEB] Steady Cow Assignment G
注意这个题目中的答案是最大 - 最小 + 1,被恶心似了。
考虑二分答案 \(x\) ,枚举最小的坐次 \(i\) ,此时所有奶牛可选区间为 \([i,i + x- 1]\)。
将每个奶牛和座位看作点,很像二分图匹配的样子。套路的建立超级源点 \(s\) 和汇点 \(t\),并让 \(s\) 向每个奶牛连边,容量为 \(1\),每个座位向 \(t\) 连边,容量为 \(v\)。
对于每个奶牛,将奶牛和所有它可匹配的座位连边,容量为 1。
答案就是网络的最大流。
标签:连边,容量,记录,网络,汇点,贡献,流做题,INF,奶牛 From: https://www.cnblogs.com/little-corn/p/18155068