前言
我们一场模拟赛的题,结果原题是新鲜出炉的。
小弟不才,感觉这题是做过的题中几乎最复杂的了。
既然搞懂了,就来写一发题解吧。
(题外话:目前最优解,我的常数真是小小又大大啊)
"Up and down,glowin' round..."
Solution
1、一个经典的 Trick
直接模拟每一种情况显然不可取,考虑计算每一条的贡献。
假设对于第 \(i\) 条,一共有 \(x_i\) 条线段能在开了水龙头后流到它(包括它自己,故 \(x_i \ge 1\))。
那么容易发现,这个位置的水龙头要打开,当且仅当它是这 \(x_i\) 条中排第一个的。
这个概率在全排列下为 \(\frac{1}{x_i}\),容易发现其他的线段对这一条贡献无影响,故答案为 \(\sum_{i=1}^{n}x_i\)。
现在我们只需要求出每一条能被多少条流到即可。
2、模拟运行,得出结论
首先按照高度从小到大排序。(本题中已经排好)
发现第 \(i\) 条(之后记为 \(a_i\))可以直接流到 \(a_j\)(\(i>j\))的条件是如下之一:
-
\(a_i\) 左右完全在 \(a_j\) 中间。
-
\(a_i\) 覆盖了 \(a_j\) 的某一个端点。(下文将这种情况称 \(a_i\) 为 \(a_j\) 的左/右祖先)
但本题可不止直接流,间接流到(\(a_i\) 流 \(a_j\),\(a_j\) 流 \(a_k\))这种也算。
经过想象和模拟,我们可以猜测能流到它的区域的两端大概是不断从左/右祖先一次一次流下来,而中间的部分都可以。
但是还有一种情况,如果 \(a_i\) 完全覆盖 \(a_j\) 以及它的所有左右祖先,那么 \(a_i\) 上面的所有线段都不可能流到 \(a_j\) 了,我们可以称 \(a_i\) 支配 \(a_j\)。
于是能流到的部分就是它不断向左右祖先去,直到被支配它的线段挡住为止。
如下图所示:
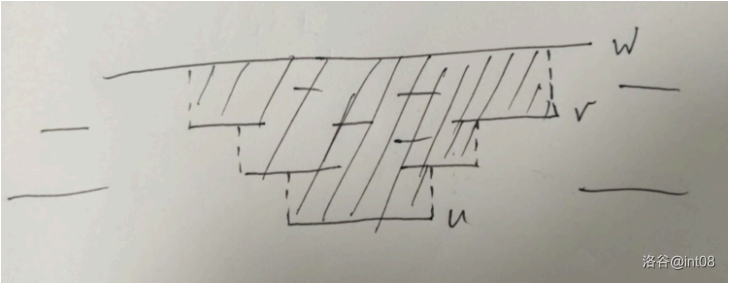
现在依次出现四个问题在我们面前,下文一一解释。
"...I saw somehow you know..."
3、解决四个问题
找到每条线段的左右祖先
由于一条线段左祖先是覆盖它的左端点的线段中高度最低(且大于它本身)的,于是从大到小扫描并使用线段树区间推平单点查询,这是简单的。
计算阴影内的线段个数
阴影部分看似是不规则的,但是我们可以用前缀相减的方式。
就像这样:
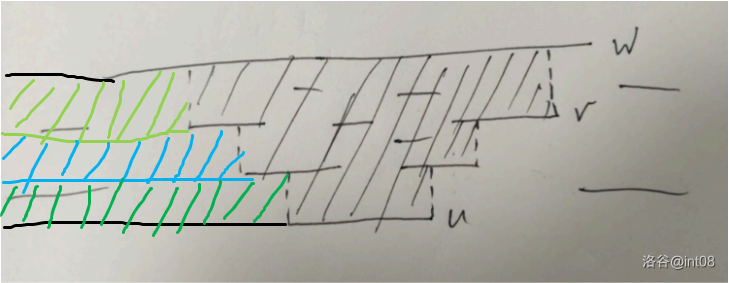
答案就是所有向右祖先跳的前缀减去所有向左祖先跳的前缀。
现在只需计算每个线段向它的祖先跳的这个 \(\text{3-side}\) 内的线段个数,等价于数右端点个数。
经典二维数点,扫描线配合树状数组搞定。
找到支配线段
为了使得每条线段都有支配线段,我们在最顶上加一条最大的线段,但是这并不影响下面的答案。
现在每条线段都被它上面的某一条支配,这形成了一棵树。
而每条线段的支配线段,就是它的左右祖先在支配树上的 \(\text{LCA}\)。
理由:要支配它得同时支配它的左右祖先,而且它左右祖先的所有祖先显然就是它的所有祖先。
而 \(\text{LCA}\) 可以使用倍增解决,倍增也支持动态加点,无敌了。
将计算答案和找到支配线段合并
很显然你可以在计算 \(\text{LCA}\) 时带权,但不只是带上本身答案这么简单。
因为左右端点的答案可能重叠。
所以对于每个点,我们应该分别记录它到支配点的左右轮廓对应的前缀和,这样合并方便,相减得出答案也不会算重。
事实上,以上内容说着简单,严谨性却有缺失,大家可以自己再思考,再证明,作为对这道题目的再利用。
AC code
代码有些难写,这题真的只有紫吗……
"...I might get down,you might not drown..."
"...You might just fly away."
#include<bits/stdc++.h>
#define N 508032
#define mod 1000000007
using namespace std;
long long qp(long long x,long long y)
{
long long ans=1;
for(long long i=1,j=x;i<=y;i*=2,j=j*j%mod) if(i&y) ans=ans*j%mod;
return ans;
}
//bit
int bit[2*N],n;
void change(int x,int y)
{
for(;x<=2*n;x+=x&-x) bit[x]+=y;
}
int ask(int x)
{
int ans=0;
for(;x;x-=x&-x) ans+=bit[x];
return ans;
}
//sgt
struct tree{
int l,r,ans;
}sgt[8*N];
#define mid ((sgt[o].l+sgt[o].r)>>1)
#define ls (o*2)
#define rs (o*2+1)
void build(int l,int r,int o)
{
sgt[o].l=l,sgt[o].r=r;
if(l==r) return;
build(l,mid,ls);
build(mid+1,r,rs);
}
void pushdown(int o)
{
if(sgt[o].ans&&sgt[o].l!=sgt[o].r)
{
sgt[ls].ans=sgt[rs].ans=sgt[o].ans;
sgt[o].ans=0;
}
}
void change(int l,int r,int v,int o)
{
pushdown(o);
if(sgt[o].l>=l&&sgt[o].r<=r)
{
sgt[o].ans=v;
return;
}
if(l<=mid) change(l,r,v,ls);
if(r>mid) change(l,r,v,rs);
}
int ask(int x,int o)
{
pushdown(o);
if(sgt[o].l==sgt[o].r) return sgt[o].ans;
if(x<=mid) return ask(x,ls);
else return ask(x,rs);
}
//LCA
struct Lca{
int lc,la,ra;
};
int d[N];
Lca p[N][23];
Lca lca(int a,int b)
{
int lans=0,rans=0;
for(int i=21;i>=0;i--)
if(d[a]<=d[b]-(1<<i))
rans+=p[b][i].ra,b=p[b][i].lc;
for(int i=21;i>=0;i--)
if(d[b]<=d[a]-(1<<i))
lans+=p[a][i].la,a=p[a][i].lc;
if(a==b) return {a,lans,rans};
for(int i=21;i>=0;i--)
{
if(p[a][i].lc==p[b][i].lc) continue;
else lans+=p[a][i].la,rans+=p[b][i].ra,a=p[a][i].lc,b=p[b][i].lc;
}
return {p[a][0].lc,lans+p[a][0].la,rans+p[b][0].ra};
}
//segment
int l[N],r[N],bel[2*N],i,j,val[N];
int lf[N],rf[N],lv[N],rv[N];
struct smx{
int id,x,k;
};
inline int read()
{
int ret=0;
char ch=getchar();
while(!isdigit(ch))
ch=getchar();
while(isdigit(ch))
ret=(ret<<3)+(ret<<1)+(ch^48),ch=getchar();
return ret;
}
vector<smx> s[N];
signed main()
{
n=read();
for(i=1;i<=n;i++) l[i]=read(),r[i]=read(),bel[++l[i]]=bel[++r[i]]=i;
n++;l[n]=1,r[n]=2*n;bel[l[n]]=bel[r[n]]=n;
build(1,2*n,1),change(1,2*n,n,1);
for(i=n-1;i>=1;i--)
lf[i]=ask(l[i],1),rf[i]=ask(r[i],1),change(l[i],r[i],i,1),
s[lf[i]].push_back({0,l[i],-1}),s[i].push_back({0,l[i],1}),
s[rf[i]].push_back({1,r[i],-1}),s[i].push_back({1,r[i],1});
for(i=n;i>=1;i--)
{
change(r[i],1);
for(auto v:s[i])
if(!v.id) lv[bel[v.x]]+=v.k*ask(v.x);
else rv[bel[v.x]]+=v.k*ask(v.x);
}
for(i=n-1;i>=1;i--)
{
Lca repair=lca(lf[i],rf[i]);
int fa=repair.lc;
val[i]=repair.ra-repair.la-lv[i]+rv[i];
d[i]=d[fa]+1;
p[i][0]={fa,repair.la+lv[i],repair.ra+rv[i]};
for(j=1;(1<<j)<=d[i];j++) p[i][j]={p[p[i][j-1].lc][j-1].lc,p[p[i][j-1].lc][j-1].la+p[i][j-1].la,p[p[i][j-1].lc][j-1].ra+p[i][j-1].ra};
}
long long ans=0;
for(i=1;i<=n-1;i++) (ans+=qp(val[i],mod-2))%=mod;
cout<<ans;
return 0;
}