审题
-
一条链
-
每条边有通行时间上下界限制
-
通过一条边需要 \(1\) 单位时间
-
站在当前节点时间减少 \(1\) 耗费 \(1\) 单位代价
-
\(q\) 次询问
-
要么更改一条边的通信时间上下界
-
要么询问在 \(b\) 时刻在城市 \(a\),\(d\) 时刻到达城市 \(c\) 的最小代价
思想
做题准备 1
我们尝试将题目直观地表示出来。
一个点(实际上是边)有一个区间,有 \(n-1\) 个点。
我们将他画在坐标系上,区间就是平行于 \(y\) 轴的线段。
虽然对于解法没有帮助,但可以帮助我们更好地思考题目。
拿样例 2 来举个例子:
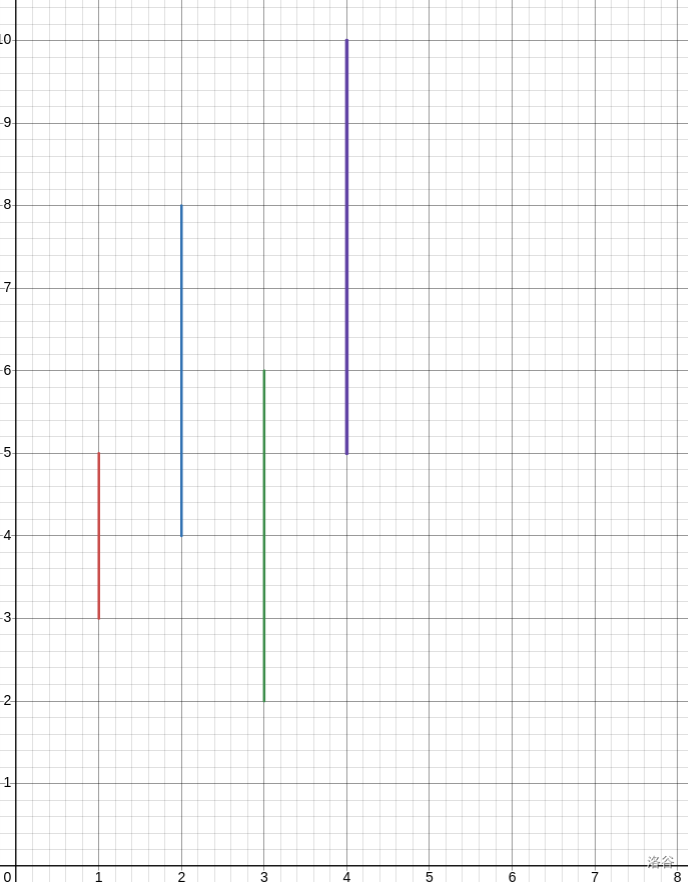
转化 1
注意到通过一条边需要 \(1\) 单位时间,而肯定不会走回头路。
我们分类讨论,把从左向右查询与从右向左分别做一遍。
我们现在看看样例 2 的从左往右的轨迹是什么样的:
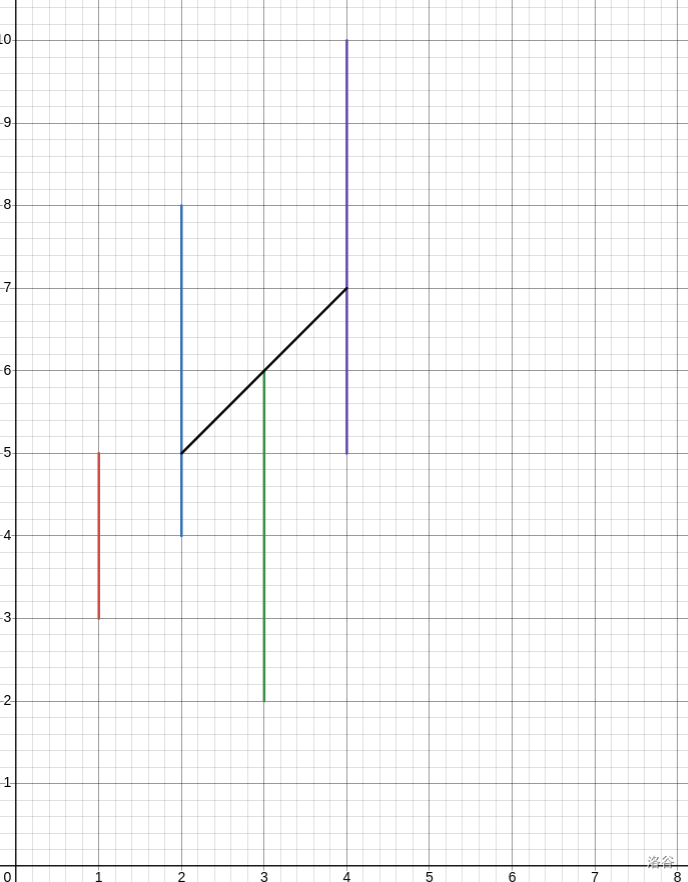
这个轨迹是斜的,很不好维护,怎么办?
把他拉成平的。
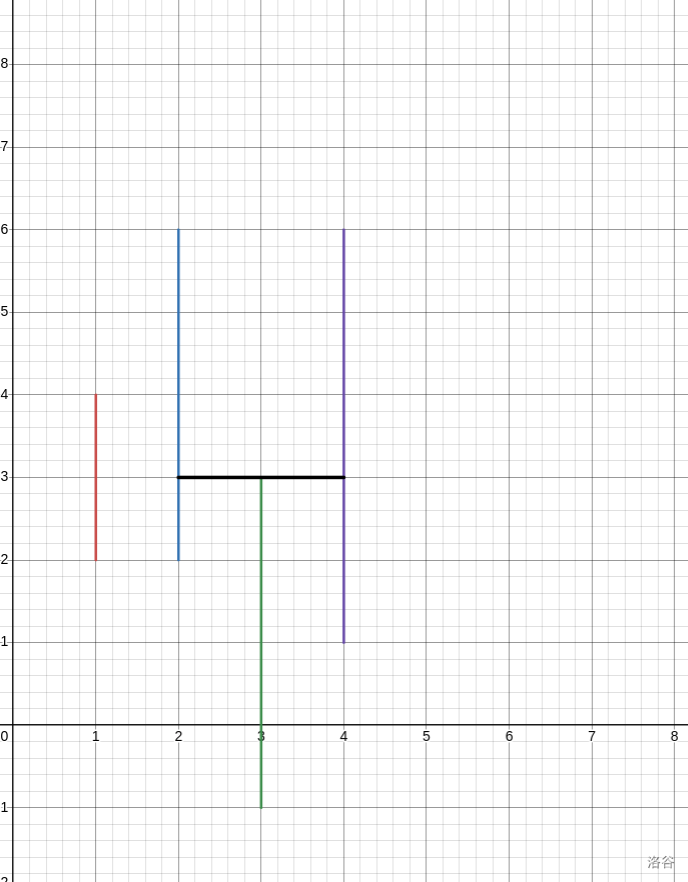
我们实际上就是将区间的左右端点都减去了 \(i\),这使得原本斜的线都变成了直线。
中间总结 1
现在我们发现如果没有时间复杂度的要求的话答案肯定是很好求的。
就是在几个线段里面走,上升,向右走不用代价,向下走要代价,要穿过中间的每个区间。
重新看一下 6 和 7。(见审题)
单点修改,区间查询。
上线段树!
步骤 1
我们很明显维护这些线段。
摆在我们面前的问题只有一个:如何合并两堆线段。
首先我们发现如果只维护答案的话,肯定是更新不了的。
我们想想能不能把一堆线段抽象成几个数。
我们先考虑最简单的情况,就是样例二的最开始的那张图。
我们如果要从最左边走到最右边那他等价于什么呢?
实际上这些区间的并不为空,这意味着,我们只要先等到或回退到这个区间的并内,就可以一条路走到底。
如图:
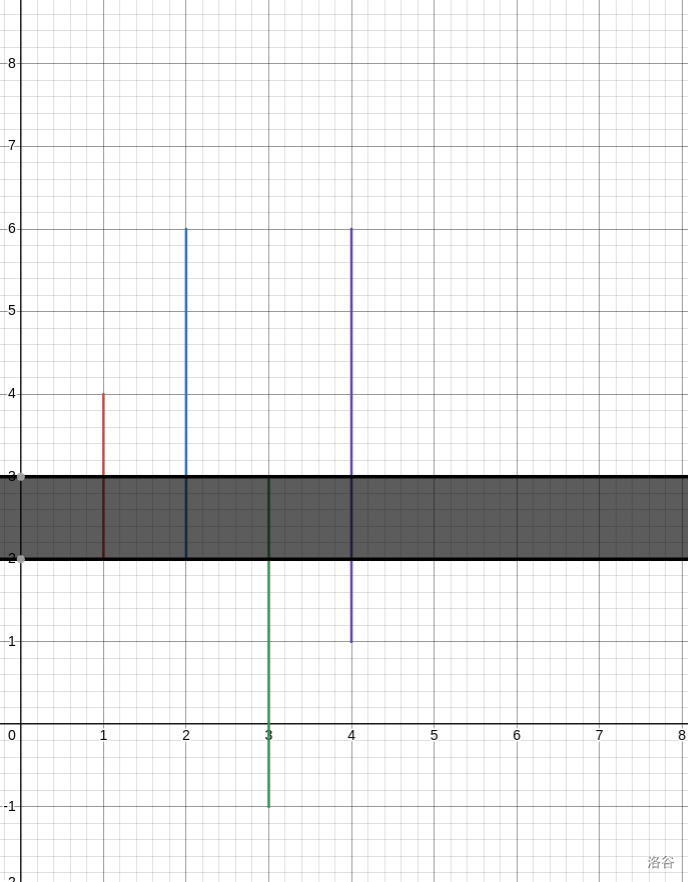
具体的话那很明显肯定是就近走到最近的在并内的点。
那还有一种情况,区间的并不为空:
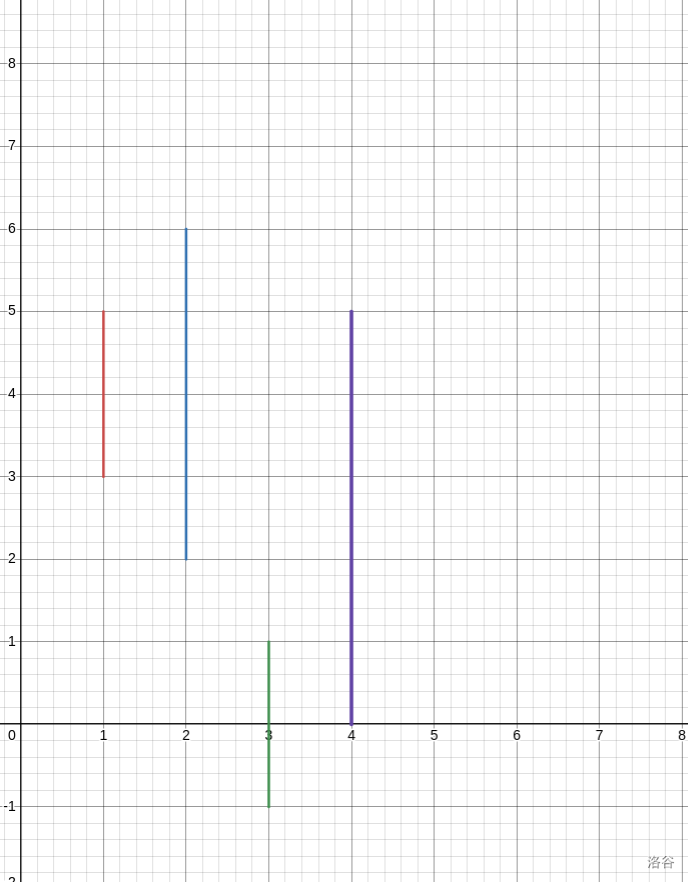
这个时候,我们将最优路线画出来:
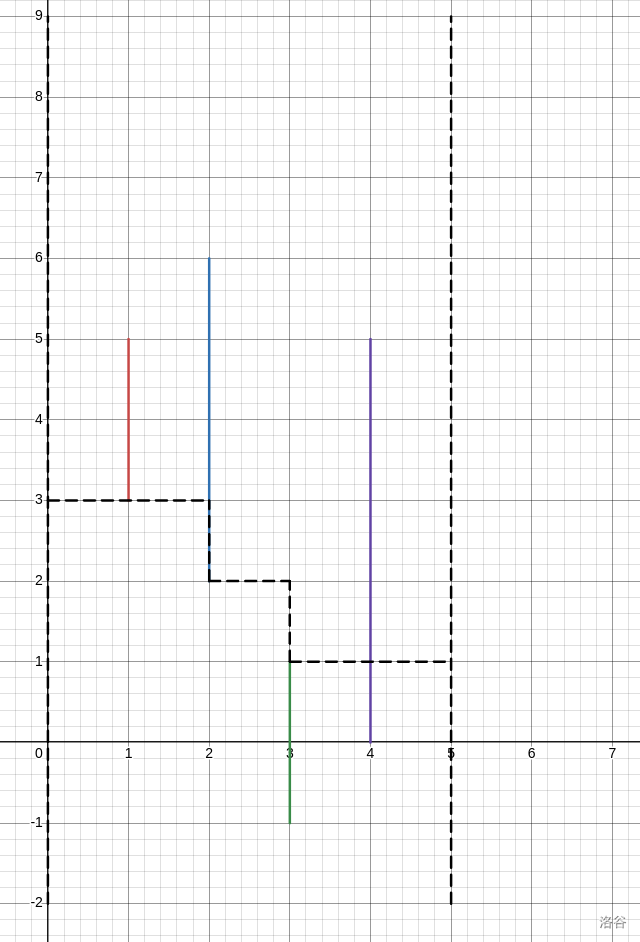
图中黑色虚线即为路径。
发现一点,我们无论从左侧哪个点开始,最优方案总是会先汇聚到一个固定的点,再走到一个固定的点,然后再发散到终点。
所以,我们就可以将一个区间由以下两种表示方式中的一种来表示:
-
这段区间的并(后文称之为二元组)
-
汇聚到了哪个点,中间花费多少代价,最终走到哪个点(后文称之为三元组)
步骤 2
我们现在想想如何合并。
分类讨论。
二元组+二元组
我们分两种情况:
-
\(1^{\circ}\) 他们的区间并不为空
我们直接将答案变成二元组,该二元组为原二元组的并
-
\(2^{\circ}\) 他们的区间并为空
第一种情况,左线段在右线段上面
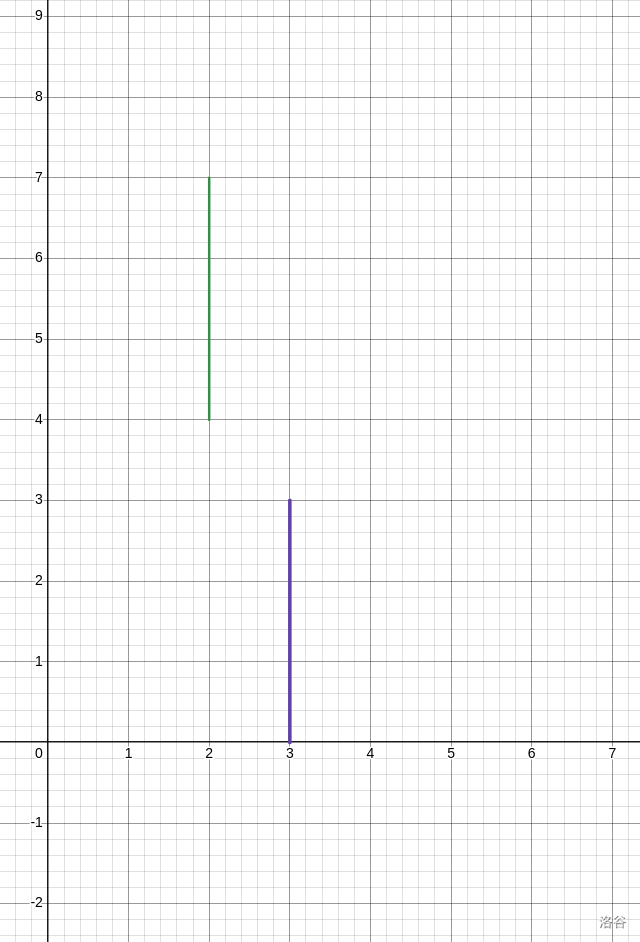
那我们就先汇聚到左线段的左端点,再走到右线段的右端点,代价为左线段左端点的时间与右线段右端点的时间差。
第二种情况,左线段在右线段下面
同理,但代价为 \(0\)。
二元组+三元组&三元组+二元组
本质等价,这里只讲二元组+三元组。
如果三元组的起点在二元组区间内,那答案三元组与原三元组一致,相当于先走到原三元组起点的时间再一路走到底,再走三元组。
如果三元组的起点在二元组区间以上,那答案三元组的起点为二元组右端点,其他与原三元组一致,相当于贴着上限走,一过了二元组就升到三元组起点位置然后走三元组。
如果三元组的起点在二元组区间之下,那答案三元组起点为二元组左端点,终点为原三元组终点,代价为二元组左端点与原三元组起点的时间差,相当于贴着下限走,一过了二元组就回到三元组起点位置然后走三元组。
三元组+三元组
这个比较简单,就是直接首位相接,代价相加,代价还要加上第一个三元组的终点到第二个三元组的起点的代价。
代码
小技巧 1
可以写一个维护二元组或三元组的结构体,然后 pushup 就变成一个输入两个结构体,输出一个结构体的函数。
这样便于将询问时把两端区间的结果合并到一起。
小技巧 2
可以写一个 solve 函数来求解单向的答案,这样双向只要 reverse 一下就可以求解了。
真正的代码
#include <bits/stdc++.h>
using namespace std;
constexpr int MAXN = 3e5 + 5;
int l[MAXN], r[MAXN], tmpl[MAXN], tmpr[MAXN];
struct Data {
int x, y;
long long z;
Data(int _x = 0, int _y = 0, long long _z = -1) {
x = _x;
y = _y;
z = _z;
}
};
Data pushup(Data lc, Data rc) {
if (~lc.z && ~rc.z)
return Data(lc.x, rc.y, lc.z + rc.z + max(lc.y - rc.x, 0));
if (~lc.z)
return Data(lc.x, max(min(lc.y, rc.y), rc.x), lc.z + max(lc.y - rc.y, 0));
if (~rc.z)
return Data(min(max(lc.x, rc.x), lc.y), rc.y, rc.z + max(lc.x - rc.x, 0));
if (max(lc.x, rc.x) <= min(lc.y, rc.y))
return Data(max(lc.x, rc.x), min(lc.y, rc.y));
if (lc.y < rc.x)
return Data(lc.y, rc.x, 0);
return Data(lc.x, rc.y, lc.x - rc.y);
}
struct SegTree {
struct Node {
int l, r;
Data data;
} tr[MAXN * 4];
void build(int k, int lp, int rp) {
tr[k] = { lp, rp, Data(l[lp], r[lp]) };
if (lp == rp)
return;
int mid = lp + rp >> 1, lc = k * 2, rc = k * 2 + 1;
build(lc, lp, mid);
build(rc, mid + 1, rp);
tr[k].data = pushup(tr[lc].data, tr[rc].data);
}
void update(int k, int p, Data v) {
if (tr[k].l == tr[k].r) {
tr[k].data = v;
return;
}
int mid = tr[k].l + tr[k].r >> 1, lc = k * 2, rc = k * 2 + 1;
if (p <= mid)
update(lc, p, v);
else
update(rc, p, v);
tr[k].data = pushup(tr[lc].data, tr[rc].data);
}
Data query(int k, int l, int r) {
if (l <= tr[k].l && tr[k].r <= r)
return tr[k].data;
int mid = tr[k].l + tr[k].r >> 1;
int lc = k * 2, rc = k * 2 + 1;
if (r <= mid)
return query(lc, l, r);
else if (l > mid)
return query(rc, l, r);
else
return pushup(query(lc, l, mid), query(rc, mid + 1, r));
}
} segtree;
int n, qq;
struct Query {
int opt, a, b, c, d;
Data ans;
} q[MAXN];
void solve() {
if (n == 1)
return;
for (int i = 1; i < n; i++)
l[i] = tmpl[i] - i, r[i] = tmpr[i] - i - 1;
segtree.build(1, 1, n - 1);
for (int i = 1; i <= qq; i++) {
if (q[i].opt == 1) {
segtree.update(1, q[i].a, Data(q[i].b - q[i].a, q[i].c - 1 - q[i].a));
} else if (q[i].a < q[i].c) {
q[i].ans = Data(q[i].b - q[i].a, q[i].b - q[i].a);
q[i].ans = pushup(q[i].ans, segtree.query(1, q[i].a, q[i].c - 1));
q[i].ans = pushup(q[i].ans, Data(q[i].d - q[i].c, q[i].d - q[i].c));
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n >> qq;
for (int i = 1; i < n; i++)
cin >> tmpl[i] >> tmpr[i];
for (int i = 1; i <= qq; i++) {
cin >> q[i].opt >> q[i].a >> q[i].b >> q[i].c;
if (q[i].opt == 2)
cin >> q[i].d;
}
solve();
reverse(tmpl + 1, tmpl + n);
reverse(tmpr + 1, tmpr + n);
for (int i = 1; i <= qq; i++) {
if (q[i].opt == 1) {
q[i].a = n - q[i].a;
} else {
q[i].a = n - q[i].a + 1;
q[i].c = n - q[i].c + 1;
}
}
solve();
for (int i = 1; i <= qq; i++) {
if (q[i].opt == 2) {
if (q[i].a == q[i].c) {
cout << max(q[i].b - q[i].d, 0) << endl;
} else {
cout << q[i].ans.z << endl;
}
}
}
return 0;
}