by TheBigYellowDuck
现阶段的水平,大概只能做 D 及以前的题了。
ARC104
[ARC104A] Plus Minus
可以得到答案为 \(\dfrac{A+B}{2}\) 和 \(\dfrac{A-B}{2}\)。
时间复杂度 \(\mathcal{O}(1)\)。
[ARC104B] DNA Sequence
对每种字符预处理前缀和。枚举子串 \([l,r]\),只需要判断子串内 A 的数量是否等于 T 的数量,以及 C 的数量是否等于 G 的数量即可。
时间复杂度 \(\mathcal{O}(n^2)\)。
[ARC104C] Fair Elevator
妙妙题。
注意到每个点都要求互不相同,最后 \(a_i,b_i\) 会遍历 \([1,2n]\) 各一次。
会发现如果存在一个区间 \((l,l+k)\),那么所有与其有交的区间都应该形如 \((l+i,l+k+i)\)。
进一步得到,只需将值域 \([1,2n]\) 划分成若干个长度为偶数的子段,每个子段 \([x,x+2k-1]\) 都用 \(k\) 个区间 \([x+i,x+k-1+i]\),\(0\leq i < k\) 完全覆盖。
现在只需要判断一个值域区间是否合法。对于一个区间 \([a_i,b_i]\),在值域上的点 \(a_i,b_i\) 标记 \(i\)。遍历值域上每一对配对的点 \((i,j)\),要求 \((i,j)\) 被同一个 \(k\) 覆盖。如果存在 \(-1\),则要求 \(a_i\) 不能作为右端点,且 \(b_i\) 不能作为左端点。
考虑 dp。令 \(f(i)\) 表示值域 \([1,i]\) 是否合法。枚举 \(j<i\),只需要判断 \([j+1,i]\) 和 \(f(j)\) 是否都合法。
时间复杂度 \(\mathcal{O}(n^3)\)。
[ARC104D] Multiset Mean
经典转化。平均数为 \(x\),可以将所有数减去 \(x\)。这样,能选的数就变成了 \((1-x) \sim (n-x)\)。只需要选出若干个数,使得和为 \(0\)。
发现 \(0\) 可以任意选 \(0 \sim k\) 个,只需要在 \([1-x,-1]\) 选出的数的绝对值之和等于 \([1,n-x]\) 选出的数的绝对值之和。前一半翻过来,就是在 \([1,x-1]\) 和 \([1,n-x]\) 分别取出一个子集,使得和相等。
设 \(f(i,j)\) 表示在 \([1,i]\) 中选数使得和为 \(j\) 的方案数。对于 \(x\) 的答案就是
\[(k+1)\left(\sum_{j=0} f(x-1,j) \times f(n-x, j)\right)-1 \]这里 \(-1\) 是因为不能选空集。
转移就是一个类似多重背包的计数过程。
\[f(i,j)=\sum_{x=0} f(i-1,j-i \times x) \]直接做是 \(\mathcal{O}(n^4k)\) 的。
这里可以做前缀和优化。正着做一遍 \(f(i,j) \leftarrow f(i,j-i)\) 这样的转移,算多的部分倒着减回去,\(f(i,j) \leftarrow -f(i,j-i\times (k+1))\)。
时间复杂度 \(\mathcal{O}(n^3k)\)。
ARC105
[ARC105A] Fourtune Cookies
对于每种情况都判断一下就好了。只有四块饼干,自然不难。
时间复杂度 \(\mathcal{O}(1)\)。
[ARC105B] MAX-=min
一开始写了一个依题意模拟,但是挂了。不是很懂。
仔细想想,会发现这个过程很类似辗转相除。实际上最后剩下的数应该就是所有数的 \(\gcd\)。
时间复杂度 \(\mathcal{O}(n +\log V)\)。
[ARC105C] Camels and Bridge
神秘题。
看到 \(n \leq 8\) 这种抽象的数据范围,不妨试试全排列能不能做。枚举所有骆驼的排列顺序,只需要算一个最小的合法距离即可。
桥 \(i\) 带来的限制大概形如,如果 \([l,r]\) 这一段骆驼的重量之和 \(\geq v_i\),那么 \(l,r\) 之间的距离 \(\geq l_i\)。对骆驼的重量做前缀和,建一张图,会发现这是个 DAG。跑一个最长路即可。
但是暴力枚举桥的限制进行建图是不可接受的。把所有桥按照 \(v_i\) 升序排序,对 \(l_i\) 做一个前缀 \(\max\),可以把连边过程改成一个二分。容易说明这样建出的图是等价的。
时间复杂度 \(\mathcal{O}(n! \times n^2 \log m)\)。
[ARC105D] Let's Play Nim
游戏分为两个阶段。先轮流选背包,后轮流取硬币。
设最终第 \(i\) 个盘子里的硬币数为 \(x_i\)。在后一阶段,根据 Nim 游戏的性质,只有当 \(x_i\) 的异或和不为 \(0\) 时先手必胜,否则后手必胜。
因为 \(n\) 的奇偶性不同,会导致选背包的过程可能让先后手调换。不妨按照 \(n\) 的奇偶性讨论。
若 \(n\) 为奇数,则先手希望异或和变成 \(0\),后手希望异或和不为 \(0\)。后手可以做这样一件事情:
- 选择硬币最多的背包,倒进硬币最多的盘子中。
这样会出现一个盘子中的硬币数比其他所有盘子中的硬币数之和还要大,自然会出现二进制下最高位异或不掉的情况,即异或和不为 \(0\)。从而后手必胜。
若 \(n\) 为偶数,则情况反过来,先手可以采取这种策略。值得注意的是存在特殊情况。如果每种数目的硬币都恰有偶数种,则后手可以完全模仿先手的操作,使得异或和为 \(0\)。其他情况都是对的。
依次判断上述事情即可。时间复杂度 \(\mathcal{O}(n \log n)\)。
[ARC105E] Keep Graph Disconnected
可以预见到,最终的必败状态必然形如,\(1\) 和 \(n\) 所在的连通块都形成了完全图,此时下一步要进行操作的人不得不将 \(1,n\) 连起来。
设最终 \(1\) 所在连通块大小为 \(x\),则一共需要操作 \(\dfrac{n(n-1)}{2}-m-x(n-x)\) 步。这个数为奇数,则先手必胜。否则后手必胜。
若 \(n\) 为奇数,则 \(x(n-x)\) 一定为偶数。只需要判断 \(\dfrac{n(n-1)}{2}-m\) 的奇偶性即可。
若 \(n\) 为偶数,会发现想要改变 \(x\) 的奇偶性需要通过合并新的大小为奇数的连通块做到。
初始局面下,设 \(1\) 所在连通块大小为 \(p\),\(n\) 所在连通块大小为 \(q\)。分类讨论。
- 若 \(p,q\) 奇偶性相同,由于总点数为偶数,所以大小为奇数的连通块有偶数个。此时若某一方合并一个连通块进来,另一方可以合并另一个平衡掉。这样令 \(x=p\) 就可以判断胜负。
- 否则,大小为奇数的连通块有奇数个。此时 \(p\times (n-q)\) 为偶数,而先手可以选择一个连通块合并进来,后续采用上述的策略,就可以获胜。
所有判据都可以用并查集维护并判断。
时间复杂度 \(\mathcal{O}(n \log n)\)。
ARC106
[ARC106A] 106
可以枚举 \(a\),算 \(n-3^a\) 是否为 \(5\) 的幂次即可。
时间复杂度 \(\mathcal{O}(\log^2n)\)。
[ARC106B] Values
显然能进行操作的必然处于一个连通块内。先用并查集维护连通性。
不妨令 \(c_i=a_i-b_i\),目标是让每个点都有 \(c_i=0\)。
注意到操作不影响连通块内点权的总和,如果 \(\sum c_i=0\),问题就变成了一个均分纸牌,显然是可以构造出解来的。用并查集顺带维护了即可。
时间复杂度 \(\mathcal{O}(n\alpha(n))\)。
[ARC106C] Solutions
第一种做法就是经典贪心,显然是正确的。
先对于一些特殊情况特判掉。
- \(m<0\) 肯定无解。因为第一种做法永远不会劣于第二种。
- \(m=0\) 构造 \(n\) 条不相交的线段即可。
- \(m=n\) 无解。因为第二种做法的答案至少为 \(1\),而答案上界为 \(n\),故不可能第一种比第二种多 \(n\)。
- \(m=n-1\) 无解。此时要求两种做法的答案分别为 \(n\) 和 \(1\),而第一种答案为 \(n\) 说明区间两两不交,故第二种的答案应该也为 \(n\)。矛盾。
对于剩下的情况,我们先构造 \(n-1\) 条两两不交的线段,再用一条左端点最小但是很长的线段盖掉前几条线段。
这样对于第一种做法的答案不会有影响,但是第二种做法就会把这条长线段选进去。那么我们想让答案差 \(m\),就只需要让这条线段盖住前 \(m+1\) 条线段即可。
时间复杂度 \(\mathcal{O}(n)\)。
[ARC106D] Powers
大力推式子。
我们希望把式子变成每一项都是完整的。先补上一些东西。
\[\sum_{i=1}^{n-1}\sum_{j=i+1}^n(a_i+a_j)^k=\dfrac{1}{2}\left(\sum_{i=1}^n\sum_{j=1}^n (a_i+a_j)^k-\sum_{i=1}^n (2a_i)^k\right) \]把前半部分拿出来接着拆。
\[\begin{aligned} \displaystyle \sum_{i=1}^n\sum_{j=1}^n (a_i+a_j)^k &= \sum_{i=1}^n\sum_{j=1}^n\sum_{r=0}^k\dbinom{k}{r}a_i^ra_j^{k-r}\\ &=\sum_{i=1}^n\sum_{r=0}^k\dbinom{k}{r}a_i^r\left(\sum_{j=1}^na_j^{k-r}\right) \\ &=\sum_{r=0}^k\dbinom{k}{r}\left(\sum_{i=1}^n a_i^r\right)\left(\sum_{j=1}^n a_j^{k-r}\right) \end{aligned} \]预处理组合数和幂和就做完了。
时间复杂度 \(\mathcal{O}(nk\log k)\)。
[ARC106E] Medals
ARC107
[ARC107A] Simple Math
分别固定三个求和号,容易发现答案就是
\[\dfrac{A(A+1)}{2} \times \dfrac{B(B+1)}{2} \times \dfrac{C(C+1)}{2} \]时间复杂度 \(\mathcal{O}(1)\)。
[ARC107B] Quadruple
考虑枚举 \(a+b\) 的值,那么 \(c+d=a+b-k\) 自然固定。现在只需要求解一个问题。
- 求数对 \((x,y)\) 的数量,满足 \(1 \leq x,y \leq n\) 且 \(x+y=S\)。
可以得到这个问题的答案为 \(f(n,S)=\min\{S-1,2n - S + 1\}\)。从而答案为
\[\sum_{x=2}^{2n} f(n,x) \times f(n,x-k) \]时间复杂度 \(\mathcal{O}(n)\)。
[ARC107C] Shuffle Permutation
注意到,交换行和交换列是互相独立的,互不影响。所以可以分别计算行和列分别能交换出多少种情况,乘起来就是答案。
不妨只考虑列。我们在能够交换的列之间连边,会发现一个连通块内可以任意排列。用并查集维护一下连通块,方案数就是每个连通块大小的阶乘的乘积。
时间复杂度 \(\mathcal{O}(n^3 \log n)\)。
[ARC107D] Number of Multisets
由于分数的存在,我们很难通过一般的背包解决。
设 \(f(i,j)\) 表示 \(n=i\) 且 \(k=j\) 时的方案数。考虑将所有方案划分成用 \(1\) 和不用 \(1\)。
如果用 \(1\),则有转移
\[f(i,j) \leftarrow f(i-1,j-1) \]如果不用 \(1\),那么将 \(k=2j\) 时选的所有数除以 \(2\) 贡献进来。
\[f(i,j) \leftarrow f(i,2j) \]时间复杂度 \(\mathcal{O}(n^2)\)。
ARC108
[ARC108A] Sum and Product
不妨设 \(n \leq m\),这样 \(n \leq \sqrt{P}\)。枚举 \(n\) 的值即可。
时间复杂度 \(\mathcal{O}\left(\sqrt{P}\right)\)。
[ARC108B] Abbreviate Fox
直接压栈,如果栈顶三个字符构成了 fox 就全都弹掉即可。
时间复杂度 \(\mathcal{O}(n)\)。
[ARC108C] Keep Graph Connected
取一个原图的生成树,只需要保留所有树边。
从根节点开始染色。设当前到考虑 \((u,v,c)\) 的一条边,如果 \(u\) 染上了 \(c\),就给 \(v\) 任意染一个和 \(c\) 不同的颜色,否则 \(v\) 染上 \(c\)。容易说明这样一定有解。所以只在图不连通时无解。
时间复杂度 \(\mathcal{O}(n+m)\)。
[ARC108D] AB
抽象题。
不妨令 \(c_{AB}=\texttt{B}\),反过来本质相同。
如果 \(c_{BB}=\texttt{B}\),那么串只能形如 \(\texttt{ABB} \cdots \texttt{B}\)。答案为 \(1\)。
如果 \(c_{BB}=\texttt{A}\),继续讨论 \(c_{BA}\) 的值。
- \(c_{BA}=\texttt{A}\),会发现所有以 \(\texttt{AB}\) 开头,以 \(\texttt{B}\) 结尾的串都可以取到。答案为 \(2^{n-3}\)。
- \(c_{BA}=\texttt{B}\),也就是 \(\texttt{A}\) 不能相邻。会发现这个东西就是斐波那契数列。
时间复杂度 \(\mathcal{O}(n)\)。
所以这个 \(n=1000\) 是在干什么。不如开到 \(n=10^{18}\)。
ARC109
[ARC109A] Hands
贪心。会发现一定是尽量用更小的一种楼梯。
如果 \(a=b\),输出 \(x\)。
如果 \(b<a\),用尽量多的走廊到达的距离是 \((2|a-b|-1)\times x\),用尽量多的楼梯到达的距离是 \((|a-b|-1)\times y+x\)。取最小值即可。
如果 \(b>a\),用尽量多的走廊到达的距离是 \((2|a-b|+1)\times x\),用尽量多的楼梯到达的距离是 \(|a-b| \times y+x\)。取最小值即可。
时间复杂度 \(\mathcal{O}(1)\)。
[ARC109B] log
直观感受,用 \(i\) 和 \(i\) 对掉是最优的,只需要让 \(n+1\) 拼出尽量多的小长度即可。
形式化地,找到最大的 \(k\) 使得 \(1+2+3+\cdots +k \leq n+1\)。长度在 \([k+1,n]\) 的木头买对应长度的即可。
可以二分 \(k\) 的值。注意 long long 乘法要开 __int128。
时间复杂度 \(\mathcal{O}(\log n)\)。
[ARC109C] Large RPS Tournament
看到这个区间长度全都为 \(2^k\) 的形式,联想到 ST 表,进而联想到倍增。
设 \(f(i,j)\) 表示从 \(i\) 开始连续 \(2^j\) 个人中胜出者的手牌。由于手牌是呈周期性变化的,区间端点可以随便取模。这样就容易记忆化搜索出来。
时间复杂度 \(\mathcal{O}(nk)\)。
[ARC109D] L
神秘题。完全做不出来。
看了一个比较简洁的 Solution。我们把平面根据起点位置按照下图的样子划分。
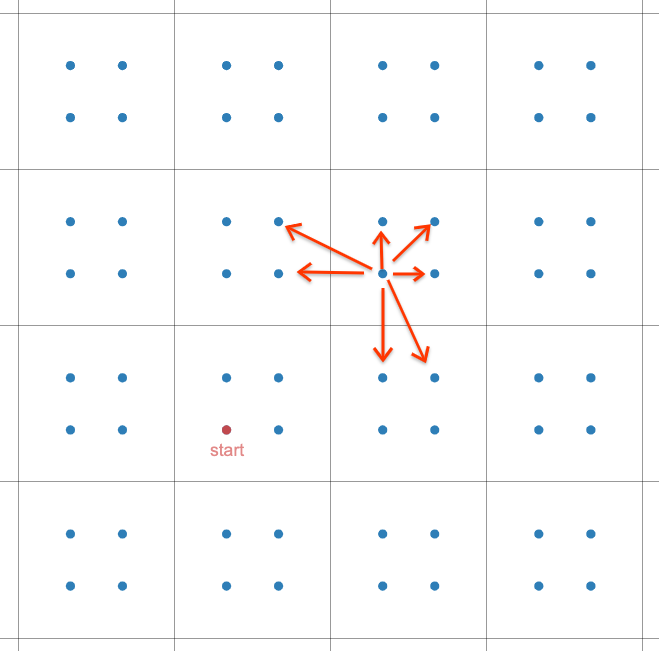
观察中心点处的移动,会发现可以在两步之内使得中心点移动到周围七个格子上。
设中心点最终被移动到 \((x_0,y_0)\),那么只需要大概 \(2\times\max\{|x_0|,|y_0|\}\) 左右的步数就可以做到了。
细节有很多。
有一个精妙实现是这样的:
\[\left\{ \begin{aligned} x_0&=a_x+b_y+c_x-\max\{a_x,b_x,c_x\} \\ y_0&=a_y+b_y+c_y-\max\{a_y,b_y,c_y\} \end{aligned} \right.\]答案是 \(\max\{|x_0|,|y_0|\}+[x_0=y_0,x_0\neq 0,x_0\neq 1]\)。
时间复杂度 \(\mathcal{O}(1)\)。
ARC110
[ARC110A] Redundant Redundancy
直观的想法是把所有数乘起来 \(+1\)。实际上只需要把质因数拆了即可。
输出 \(2^4\times 3^3\times 5^2\times 7\times11\times13\times17\times19\times23\times29+1\)。
[ARC110B] Many 110
感觉想复杂了。但是避免掉了一些可能的分类讨论?
先用一个长度为 \(3n\) 的串 \(\texttt{110110}\cdots\texttt{110}\) 和 \(T\) 匹配,匹配不上答案就是 \(0\),否则找到第一次匹配的位置。根据 \(T\) 末尾两位判断最后一次匹配在哪里,直接相减即可。
时间复杂度 \(\mathcal{O}(n)\)。
[ARC110C] Exoswap
由于每个位置被定死只能交换一次,从而每个数的位置必然一直减小或一直增加。
会发现需要交换 \((i,i+1)\) 当且仅当 \(A_i>i\) 且 \(A_{i+1}<i+1\)。并且需要让 \(A_i\) 和 \(A_{i+1}\) 归位就必然要进行这次操作,与什么时候进行无关。
我们把所有要交换的数对扔进队列里,每次拿出来队首 \((i,i+1)\) 交换,再判断一下 \((i-1,i)\) 和 \((i+1,i+2)\) 需不需要交换即可。
时间复杂度 \(\mathcal{O}(n)\)。
[ARC110D] Binomial Coefficient is Fun
记 \(S=\sum a_i\)。
将 \(S\) 个黑球排成一列,每组之间的 \(n-1\) 个空隙中放上一块隔板。这样会产生 \(n+S\) 个空隙。将不超过 \(m-S\) 个白球插入到空隙之中,可以为空,求方案数。
考虑组合意义。令 \(b_i\) 为同一组内黑球和白球的总和,容易说明这两个问题是等价的。则答案为
\[\sum_{i=0}^{m-S}\binom{i+n+S-1}{n+S-1}=\binom{n+m}{m-S}=\binom{n+m}{n+S} \]发现 \(n+S\) 大约是 \(4\times 10^6\) 级别,直接摁算组合数即可。
时间复杂度 \(\mathcal{O}(n+\sum a_i)\)。
ARC111
[ARC111A] Simple Math 2
对于这个下取整,分子上没有取模的情况下是很难算的。
注意到取整是可以从取整符号里面拿出来一些整数的,不妨 \(10^n\) 中拿出来若干个 \(m^2\),这样在模 \(m\) 意义下答案不会改变。所以我们对 \(10^n\) 模上 \(m^2\) 即可。
时间复杂度 \(\mathcal{O}(\log n)\)。
[ARC111B] Reversible Cards
在一张牌的 \(a_i,b_i\) 之间连边,要对每条边都选择一个端点,使得被选择的不同端点数量最大。
不妨对连通块考虑。对于一个点数为 \(n\),边数为 \(m\) 的连通块,进行分类讨论。
- \(m=n-1\),则此时连通块为一棵树。钦定一个点为根,每条边选儿子即可做到 \(n-1\)。
- \(m\geq n\),找到一个环,容易说明环上的点可以全被选中。把环上的边都删掉。一直做下去会发现可以选中每个点。
所以每个连通块的答案就是 \(\min\{n,m\}\)。并查集维护连通性即可。
时间复杂度 \(\mathcal{O}(n \log n)\)。
[ARC111C] Too Heavy
感性理解,应该只有初始状态时存在 \(a_i \leq b_{p_i}\) 时无解。先判掉。
现在 \(a_i \gt b_{p_i}\)。考虑在 \(i \rightarrow p_i\) 连边,会得到若干个环。这样交换 \(i,j\) 就相当于一个环上的分裂过程。我们的目标是得到 \(n\) 个自环。
对于每个环,找到 \(x\) 使得 \(a_x\) 为环上 \(a\) 的最小值,并找到 \(x\) 的前驱 \(y\)。交换 \(x,y\) 会达到让 \(x\) 连成自环的效果。而由于 \(b_{p_x}<a_x<a_y\),从而让 \(p_y=p_x\) 不会使 \(y\) 变成不合法。
重复这个过程就可以断掉所有长度 \(\geq 2\) 的环。每次操作都会让环的长度 \(-1\),刚好能达到操作次数下界。
时间复杂度 \(\mathcal{O}(n \log n)\)。
[ARC111D] Orientation
发现如果 \(c_x<c_y\),那么只能定 \(x \leftarrow y\)。否则 \(x\) 可以走到 \(y\) 能走到的所有点,这样 \(c_x\) 必然不可能小于 \(c_y\),就矛盾了。同理,当 \(c_x>c_y\) 时也只能定 \(x\rightarrow y\)。
难点在于处理 \(c_x=c_y\) 的情况。把剩下的点按照 \(c\) 分组,考虑将 \(c\) 相同的串成环,这样彼此之间不会产生矛盾。那么先在 \(x,y\) 之间连一条无向边,再定向即可。
另外一种很厉害的构造。观察到“串成环”的本质是为了让这些点强连通。把这些点拿出来 DFS,树边由父亲指向儿子,返祖边由后代指向祖先即可。
因为保证了有解,所以上述两种方案都没有问题。其中第二种要求没有割边。
时间复杂度 \(\mathcal{O}(n+m)\)。
ARC112
[ARC112A] B = C
先固定 \(C\) 的值,再遍历 \(B\) 的值。容易得到答案为 \(\dfrac{(r-2l+1)(r-2l+2)}{2}\)。
时间复杂度 \(\mathcal{O}(1)\)。
[ARC112B] -- - B
考虑最后能走到的大概会形成不超过两个区间。当 \(C\) 足够大时形成一个,否则形成两个。
不妨认为 \(B>0\),对于 \(B<0\) 可以直接交换上下界。
在正半轴上留下的最长足迹。向负方向不断 \(-1\) 就行,向正方向应该先 \(\times (-1)\),不断 \(-1\) 之后再负回来。这段区间应该是 \(\left[B-\dfrac{C}{2},B+\dfrac{C-2}{2}\right]\)。
在负半轴上留下的最长足迹。向负方向应该先 \(\times (-1)\) 再不断 \(-1\),向正方向应该先 \(-1\) 再负回去。这段区间应该是 \(\left[-B-\dfrac{C-1}{2},-B+\dfrac{C-1}{2}\right]\)。
如果两段区间有交,减掉重复即可。特殊地,对于 \(B=0\),答案就是 \(C\),要特判掉。
时间复杂度 \(\mathcal{O}(1)\)。
[ARC112C] DFS Game
好玩题。
发现,如果 \(u\) 子树大小为奇数,那么先手把棋子从 \(\text{fa}(u)\) 移动进子树 \(u\) 直到移动回 \(\text{fa}(u)\) 的过程结束后,决策权会给到先手。也就是说,如果子树大小为奇数,遍历这个子树会导致决策权交换。
玩家如何决策是由子树内的状态影响的,考虑树形 dp 来决策。
设 \(f(u)\) 表示在 \(u\) 时先手决策的答案。钦定先手拿了 \(u\) 处的硬币,让后手决定应该进入哪个儿子 \(v\)。
令 \(\text{size}(u)\) 表示 \(u\) 的子树大小。那么 \(\text{size}(u)-f(u)\) 就是后手得到的硬币,记为 \(f'(u)\)。
- \(\text{size}(v)\) 为偶数。此时后手把棋子移动到 \(v\) 子树中并回到 \(u\) 之后,下一次进入哪棵子树仍然由后手决策。那么自然后手要先遍历掉 \(f'(v) \geq f(v)\) 且最大的几棵子树。
- \(\text{size}(v)\) 为奇数。此时后手遍历完 \(v\) 子树后会导致决策权交换,此时后手会希望得到尽量优秀的子树,也就是 \(f'(v)-f(v)\) 最大的子树。
考虑 \(f\) 的转移。
-
对于第一类情况,
- 若 \(f'(v) \gt f(v)\),则后手会拿掉 \(f'(v)\),先手的收益是 \(f(v)\)。\(f(u) \leftarrow f(v)\)。
- 若 \(f'(v) \leq f(v)\),则后手会避免先走 \(v\),并最后留给先手自己走。\(f(u) \leftarrow f'(v)\)。
-
对于第二类情况,对 \(f'(v)-f(v)\) 排序,轮流走最大的。
现在就得到了一个过程。先手拿掉 \(u\) 处的硬币,后手先走第一类,两人轮流取第三类,最后根据决策权换到了谁手里来决定谁被迫走掉第二类。
时间复杂度 \(\mathcal{O}(n \log n)\)。
[ARC112D] Skate
考虑在格子 \((i,j)\) 设置 # 的实际意义。一个 # 提供了一个转向的机会,也就是可以从覆盖第 \(i\) 行转向覆盖第 \(j\) 列。我们要覆盖所有行列。
将行和列作为二分图的左右部点,会发现一个 \((i,j)\) 是在左部 \(i\) 和右部 \(j\) 之间连边。四个墙角提供了 \((1,1),(1,m),(n,1),(n,m)\) 四条边。而我们要做的是让左右部点完全联通。
并查集维护加边即可。时间复杂度并查集外线性。
ARC113
[ARC113A] A*B*C
不妨设 \(A\leq B \leq C\),得到 \(A\leq \sqrt[3]{K}\),\(B \leq \sqrt{K}\)。枚举 \(A,B\) 的值,算 \(C\) 的范围即可。
时间复杂度 \(\mathcal{O}(K^{5/6})\)。
[ARC113B] ABC
只需考虑 \(A\) 的个位,对于 \(0 \sim 9\) 中的每一个数,若干次幂之后的各位数都是有周期的。把周期都打表出来,这样指数上的 \(B^C\) 就可以取模了。
时间复杂度 \(\mathcal{O}(\log C)\)。
[ARC113C] String Invasion
观察到,如果存在 \(s_i=s_{i+1} \neq s_{i+2}\),那么 \(s_i\) 可以将后面所有字符都推平。那么最优策略就是从后往前扫,能推都全都推平。
但是当 \(s_i=s_{i+1}=s_{i+2}\) 时,虽然可以推平,但是不计入操作次数。对每种字符记录一下后缀和,推平的时候动态更新一下即可。
时间复杂度 \(\mathcal{O}(|S||\Sigma|)\)。
[ARC113D] Sky Reflector
\(A,B\) 互相有影响会让处理问题很复杂,尝试把 \(A,B\) 分开独立处理。
观察到一个性质:
\[\min_{i=1}^n A_i \leq \max_{i=1}^m B_i \]证明可以设 \(A_x=\min_{i=1}^n \{A_i\}\),\(B_y=\max_{i=1}^m \{B_i\}\)。则有 \(A_x \leq G_{x,y} \leq B_y\)。
如果钦定 \(\min_{i=1}^n \{A_i\}=x\),那么 \(A,B\) 的数量就都可以得到。我们考虑能否对于一对 \((A,B)\) 构造出一个合法的矩阵。
尝试归纳构造。对于 \(n=m=2\),可以构造出如下的矩阵 \(G\)。
\[\begin{bmatrix} A_1&B_2 \\ B_1&A_2 \end{bmatrix} \]对于 \(n=i\) 的构造推 \(n=i+1\),只需要把 \(A_{i+1}\) 随便扔到第 \(i+1\) 行的某个位置上即可。上面的性质保证了 \(A\) 不会和 \(B\) 产生冲突。对于 \(m=i\) 推 \(m=i+1\) 同理。
这样只需要枚举 \(x\)。合法的 \(A\) 种类数有 \(x^n-x^{n-1}\),合法的 \(B\) 种类有 \((k-x+1)^m\)。乘起来求和即可。
时间复杂度 \(\mathcal{O}(k \log n)\)。
ARC114
[ARC114A] Not coprime
一个看着很对的想法是把 \(X_i\) 的最小质因子并起来,但是这实际上是错的。比如 \(22,33,55\) 这么做会得到 \(2\times 3\times 5=30\),然而 \(11\) 就可以满足。
注意到 \(X_i\leq 50\),而 \(50\) 以内的质数只有 \(15\) 个。暴力枚举这些质数的子集即可。
时间复杂度 \(\mathcal{O}(2^{\pi(X_i)}\times n)\)。
[ARC114B] Special Subsets
自然想到 \(i \rightarrow f_i\) 连有向边,那么每个连通块都是一个基环内向树。
考虑第二条限制,会发现要求我们对于每个连通块只能选整个环,环外的点都不能选。也就是说,每个连通块的选取方案是唯一的,只有选和不选。
设一共形成了 \(t\) 个连通块,那么答案就是 \(2^t-1\)。并查集维护一下即可。
时间复杂度 \(\mathcal{O}(n)\)。
[ARC114C] Sequence Scores
有趣的题目。
先考虑对于一个固定的 \(A\) 序列怎么最小化操作次数。对于下标 \(i<j\),如果 \(A_i=A_j\) 且它们之间的高度都比它们更大,那么我们可以一次操作同时做掉 \(i,j\)。
把这样的 \(i,j\) 合并到一个连通块内,那么最后连通块个数就是最小的操作次数。
显然合并过程只需要与最近的点合并就可以达到连通的效果,也就是如果存在 \(i<j<k\) 都可以合并到一起,那么只需要合并 \(i,j\) 和 \(j,k\) 即可。
对于所有 \(A\),考虑拆贡献。对于一个连通块,我们只在其最小的端点处计算贡献。先认为所有点的做了贡献,再把多余的贡献减掉即可。
总贡献为 \(n\times m^n\)。一个点 \(i\) 会在与其前面某个点相连时多算了贡献,设 \(i\) 与前面的 \(j\) 合并了,需要先钦定 \(i,j\) 的颜色和 \(i,j\) 之间的点的颜色, \(i,j\) 之外的点的颜色任意。
\[\sum_{x=1}^m (m-x)^{i-j-1}\times m^{n-(i-j+1)} \]总的额外贡献就是
\[\sum_{i=1}^n\sum_{j=1}^{i-1}m^{n-(i-j+1)}\sum_{x=1}^m(m-x)^{i-j-1} \]朴素计算,时间复杂度 \(\mathcal{O}(n^2m)\)。
注意到这个式子的值只与 \(x\) 和 \(i-j\) 有关,可以枚举 \(x\) 以及 \(i-j\)。时间复杂度降至 \(\mathcal{O}(nm)\)。
[ARC114D] Moving Pieces on Line
[ARC114E] Paper Cutting 2
ARC115
[ARC115A] Two Choices
把每个学生的答案看成二进制数,那么永远不会相同等价于 \(\text{popcount}(a_i \oplus a_j)\) 为奇数。
更进一步,可以转化为 \(\operatorname{popcount}(a_i)+\operatorname{popcount}(a_j)\) 为奇数,等价于 \(a_i\) 与 \(a_j\) 的 \(\operatorname{popcount}\) 的奇偶性不同。统计一下奇数个 \(1\) 和偶数个 \(1\) 分别有多少个数,乘起来即可。
时间复杂度 \(\mathcal{O}(nm)\)。
[ARC115B] Plus Matrix
直接取 \(A_i=\min C_{i,j}\),让 \(C_{i,j}\) 减去 \(A_i\)。如果剩下每列的数都相等,那么 \(B\) 就得到了,否则无解。
感觉正确性是显然的。时间复杂度 \(\mathcal{O}(nm)\)。
[ARC115C] ℕ Coloring
一个不需要动脑子的做法。
\(i\) 的每个约数向 \(i\) 连有向边,那么答案就是从 \(1\) 开始的最长路。
时间复杂度 \(\mathcal{O}(n\ln n)\)。
[ARC115D] Odd Degree
好题。
如果原图是一棵树,那么选择 \(k\) 个奇度点的方案是就是 \(\dbinom{n}{k}\)。考虑构造性证明,选出这 \(k\) 个点之后从叶子自底向上考虑怎么选边,会发现选取方案是唯一确定的。
如果原图有环,随便取一棵生成树,先任选非树边的状态,再钦定 \(k\) 个奇度点,在非树边的影响下选取方案仍然是唯一的。那么方案数就是 \(2^{m-(n-1)}\times\dbinom{n}{k}\)。
如果原图有多个连通块,设 \(f(i,j)\) 表示前 \(i\) 个连通块中钦定了 \(j\) 个奇度点的答案,在第 \(i\) 个连通块中钦定 \(k\) 个奇度点,背包合并即可。由于度数之和必须是偶数,所以 \(k\) 要是偶数。
时间复杂度 \(\mathcal{O}(n^2)\)。
[ARC115E] LEQ and NEQ
好题。双倍经验 CF1591F。
考虑容斥。设 \(f_i\) 表示至少出现了 \(i\) 对相邻相同数的方案数,那么答案就是
\[S=\sum_{i=0}^{n-1}(-1)^if_i \]我们把连续的相邻相同数看成一个段,会发现出现 \(i\) 对其实可以看作将序列切成 \(n-i\) 段,其中每一段中的数相等。注意,段与段之间不必要不相等,因为我们求的是至少。
考虑对这个东西做 dp。设 \(f(i,j)\) 表示前 \(i\) 位切成 \(j\) 段的方案数,枚举上一段的末尾进行转移。
\[f(i,j)=\sum_{k<i}f(k,j-1)\times\min_{t=k+1}^ia_t \]后面这个 \(\min\) 的意义为,我们想把 \([k+1,i]\) 染成一种颜色,有多少种方法。显然是取上限的最小值。
直接转移复杂度爆炸。我们把 dp 式子写进容斥的式子里。
\[S=\sum_{i=0}^{n-1}(-1)^i\times f(n,n-i) \]会发现其实只需要关心 \(n-i\) 的奇偶性,用偶数段和奇数段的方案数相减即可。
改写 dp 式子,设 \(f(i,0/1)\) 表示前 \(i\) 位切成偶数段/奇数段的方案数。\(j\) 这一维就压掉了。
现在考虑怎么压掉 \(\min\)。观察到对于 \(a_i\) 可以作为最小值的作用区间内,\(\min a_t\) 的值是一样的,那么前面的 \(f\) 就可以用前缀和优化掉。
这件事情启发我们尝试单调栈。设 \(a_i\) 左边第一个小于 \(a_i\) 的位置为 \(p\),考虑从 \(p\) 直接转移。
- 如果 \(p\) 不存在,那么 \(a_i\) 就是最小值,直接用前缀和 \(\times a_i\) 转移过来即可。
- 存在 \(p\),那么 \(f(1\cdots (p-1),op \oplus 1)\) 都可以转移到 \(f(i,op)\)。然而我们发现,这一段的转移乘上的系数是 \(a_p\),与 \(a_i\) 无关,并且这一部分的贡献都已经转移到了 \(f(p,op)\)。那我们直接用 \(f(p,op)\) 作为 \(p\) 之前的所有转移的贡献总和即可。
时间复杂度 \(\mathcal{O}(n)\)。
ARC116
[ARC116A] Odd vs Even
对 \(N\) 质因数分解,考察其含 \(2\) 的个数。
- 如果 \(v_2(N)=1\),那么一个奇因数乘以 \(2\) 就对应一个偶因数,数量相等。
- 如果 \(v_2(N)>1\),那么偶因数多,否则奇因数多。
时间复杂度 \(\mathcal{O}(1)\)。
[ARC116B] Products of Min-Max
先排序。从小到大钦定 \(a_i\) 作为最大值,那么其能产生的贡献为
\[a_i\sum_{j<i}a_j\times 2^{i-j-1} \]把只与 \(i\) 有关的东西提出来
\[2^ia_i\sum_{j<i}\dfrac{a_j}{2^{j-1}}=2^ia_i\times\dfrac{1}{2}\left(\sum_{j<i}\dfrac{a_j}{2^j}\right) \]预处理 \(2^i\) 的逆元和前缀和就可以了。
时间复杂度 \(\mathcal{O}(n)\)。
[ARC116C] Multiple Sequences
考虑枚举 \(a_n\),对其分解质因数得到
\[a_n=p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k} \]不妨设 \(a_0=1\),令 \(x_i=\dfrac{a_{i}}{a_{i-1}}\),则有
\[x_1x_2\cdots x_n=a_n$$我们只需要将 $a_n$ 的质因子分配给 $x_i$。 那么这就是一个插板法了。对于每个指数 $\alpha_i$,都有 $\dbinom{n+\alpha_i-1}{\alpha_i}$ 种分配方法。同时每一种质因子之间相互独立,从而答案为 $$\prod_{i=1}^k\dbinom{n+\alpha_i-1}{\alpha_i}\]时间复杂度 \(\mathcal{O}(n\log n)\)。
[ARC116D] I Wanna Win The Game
由于异或每一位上独立,如果我们知道了最后一位有多少个 \(1\),可以将所有数右移一位,得到新的更小的目标和。这个新问题就变成了原问题的一个子问题。
基于这个想法,令 \(f(i)\) 表示长度为 \(n\) 的序列总和为 \(i\),异或和为 \(0\) 的方案数。枚举最后一位上 \(1\) 的个数 \(j\) 进行转移。
\[f(i)=\sum_{j\leq i}\dbinom{n}{j}f\left(\dfrac{i-j}{2}\right) \]时间复杂度 \(\mathcal{O}(nm)\)。
[ARC116E] Spread of Information
二分答案,转化为判定问题,只需判断最大距离为 \(x\) 时能否用 \(k\) 个点覆盖。
考虑一个贪心策略:对于以 \(u\) 为根的子树,我们选 \(u\) 当且仅当 \(u\) 距离其子树内最深的点恰为 \(x\)。否则在 \(u\) 的父亲放也能覆盖到 \(u\) 子树内的点,而且能覆盖到更多 \(u\) 子树外的点,一定不劣。
令 \(f(u)\) 表示以 \(u\) 为根的子树中距离 \(u\) 最近的关键点到 \(u\) 的距离,\(g(u)\) 为以 \(u\) 为根的子树中距离 \(u\) 最远的未被覆盖到的点到 \(u\) 的距离。则有
\[f(u)=\min_{(u,v)}\{f(v)+1\} \]\[g(u)=\max_{(u,v)}\{g(v)+1\} \]考虑一些特殊情况:
- 如果 \(f(u)+g(u)\leq x\),说明 \(u\) 子树中任意一点都可以仅靠子树内选的点覆盖掉。可以令 \(g(u)=-\infty\)。
- 如果 \(g(u)=x\),说明必须要让 \(u\) 作为关键点覆盖掉,可以令 \(f(u)=0\),\(g(u)=-\infty\)。
考虑做完之后树上所有 \(g(u)\geq 0\) 的点,\(u\) 子树内的点都被覆盖掉了,而 \(u\) 需要依靠其子树外的点来覆盖。而根节点没有子树外的点了,要特判一下。
时间复杂度 \(\mathcal{O}(n\log n)\)。
ARC117
[ARC117A] God Sequence
当 \(A=B\) 时,构造 \(\pm i\),\(1\leq i\leq A\) 即可。
当 \(A<B\) 时,构造 \(B\) 项 \(-1,-2,\cdots,-B\),同时记 \(S=-(1+2+\cdots+B)\),只需要再构造 \(A\) 项 \(1,2,\cdots,A-1,S+(1+2+\cdots+(A-1))\) 即可。当 \(A>B\) 时同理。
时间复杂度 \(\mathcal{O}(A+B)\)。
[ARC117B] ARC Wrecker
不妨先排序,令 \(a_0=0\)。
注意到相同元素会一起减小,那么把 \(a_i\) 调到 \(a_{i-1}\) 后两个元素就可以合并。那么答案就是
\[\prod_{i=1}^n(a_i-a_{i-1}+1) \]时间复杂度 \(\mathcal{O}(n)\)。
[ARC117C] Tricolor Pyramid
把三种颜色看成 \(0,1,2\),那么这个放置的限制相当于要求 \(3\mid (a+b+c)\)。
设最顶上的元素是 \(a\),下面两个是 \(b_1,b_2\),则有 \(a+b_1+b_2\equiv 0\pmod 3\),设下面一层是 \(c_1,c_2,c_3\),则有 \(a-c_1-2c_2-c_3\equiv 0\pmod 3\)。如此做下去,设最下面一层是 \(x_1,x_2,\cdots,x_n\),则有
\[a+(-1)^n\sum_{i=0}^{n-1}\dbinom{n-1}{i}x_{i+1}\equiv 0\pmod 3 \]这样就只需要算一下最后一层即可。
计算组合数模 \(3\) 可以用卢卡斯定理。注意 Lucas 的写法。
时间复杂度 \(\mathcal{O}(n\log n)\)。
[ARC117D] Miracle Tree
对点权排序,从小到大设为 \(E_{p_1},E_{p_2},\cdots,E_{p_n}\)。这样把限制转化成了只需要 \(E_{p_{i+1}}-E_{p_i}\geq \operatorname{dis}(p_{i+1},p_i)\)。证明考虑 \(E_i-E_j+E_j-E_k\geq \operatorname{dis}(i,j)+\operatorname{dis}(j,k)\geq \operatorname{dis}(i,k)\)。
现在我们要最小化 \(E_i\),直接让上述不等式取等,转化为 \(E_{p_{i+1}}-E_{p_i}=\operatorname{dis}(p_{i+1},p_i)\)。这样最大值
\[E_{p_n}=E_{p_1}+\sum_{i=1}^{n-1}\operatorname{dis}(p_{i+1},p_i)\geq1+\sum_{i=1}^{n-1}\operatorname{dis}(p_{i+1},p_i) \]我们还要最小化 \(E_{p_n}\),可以直接钦定 \(E_{p_1}=1\)。
又注意到
\[\operatorname{dis}(p_1,p_n)+\sum_{i=1}^{n-1}\operatorname{dis}(p_{i+1},p_i)=2(n-1) \]这相当于遍历一棵树并回到起点。
这样我们只需要最大化 \(\operatorname{dis}(p_1,p_n)\)。取 \(p_1,p_n\) 为直径端点即可。
现在我们要找到一个 dfs 序使得 \(p_1\) 被第一个遍历到,\(p_n\) 被最后一个遍历到。把直径上的点打上标记,遍历子树时先遍历没有打标记的点,再遍历打了标记的点。
注意答案不是直接输出 dfs 序。记得再算一下每个点的点权,可以维护一个变量,进出子树时都加一下。
时间复杂度 \(\mathcal{O}(n)\)。
[ARC117E] Zero-Sum Ranges 2
[ARC117F] Gateau
不妨认为 \(A_i\) 是循环的,即 \(A_{2n}=A_0\)。
设 \(b_i\) 为第 \(i\) 块蛋糕上的数量。让 \(b_i\) 的下标从 \(0\) 开始,维护 \(b_i\) 的前缀和。
特殊地,令 \(S_0=0\)。对于 \(i\geq 1\),定义
\[S_{\textcolor{red}{i}}=\sum_{j=0}^{\textcolor{red}{i-1}} b_j \]忽略掉跨过链两端的限制,剩下的限制都可以写成 \(S_{i+n}-S_i\geq A_i\) 的形式。跨过链两端的限制是一个前缀和一个后缀,未被覆盖的区域是一个区间。
记 \(X=\sum b_i\)。那么跨过链两端的限制可以写成 \(X-(S_i-S_{i-n})\geq A_i\)。
一个前缀和序列 \(S_0,S_1,S_2,\cdots,S_{2n}\) 合法,需要满足以下条件:
- \(S_i\leq S_{i+1}\)。
- \(S_0=0\),\(S_{2n}=X\)。
- 对于 \(i\in [0,n-1]\),\(S_{i+n}-S_i\geq A_i\)。
- 对于 \(i\in [n,2n]\),\(S_i-S_{i-n}\leq X-A_i\)。
更进一步整理可以得到
- \(0=S_0\leq S_1\leq\cdots\leq S_{2n}=X\)。
- 对于 \(i\in [0,n]\),\(A_i\leq S_{i+n}-S_i\leq X-A_{i+n}\)。
容易说明当 \(X\) 充分大时一定有解,可以二分答案 \(X\)。所有不等式限制都可以写成差分约束的形式,建图套差分约束即可。
因为有负权边,所以需要 spfa。然而数据范围并不支持,我们只能挖掘一下这张图的性质。
按照差分约束,建出来的图应该只有以下这些边:
- \(i+1\) 向 \(i\) 连权值为 \(0\) 的边。
- \(0\) 向 \(2n\) 连权值为 \(X\) 的边,\(2n\) 向 \(0\) 连权值为 \(-X\) 的边。
- 对于 \(i\in[0,n]\),\(i\) 向 \(i+n\) 连权值为 \(X-A_{i+n}\) 的边,\(i+n\) 向 \(i\) 连权值为 \(-A_i\) 的边。
我们只需要判断该图存不存在负环。容易说明 \(A_i+A_{i+n}\leq X\),从而负环要么经过点 \(n\),要么经过 \(2n\rightarrow 0\) 的这条边。
我们把点 \(n\) 和 \(0\) 到 \(2n\) 之间的边删掉,会发现整张图是由 \(n-1\rightarrow n-2\rightarrow\cdots\rightarrow 0\) 和 \(2n\rightarrow2n-1\rightarrow\cdots\rightarrow n+1\) 两条链组成,另外在 \((i,i+n)\) 之间存在一对权值和 \(\geq 0\) 的边。

显然这个新图中不存在负环,并且结构很清晰。只能从右往左走,且在同一位置上下穿梭不会使得路径变短。
我们可以通过 dp 求出 \(0,2n,n-1,n+1\) 两两之间的最短路,再将 \(n\) 号点和 \(0\) 到 \(2n\) 之间的边加上,判断这五个点构成的图是否存在负环即可。
针对这个链状结构,不妨设 \(f(i)\) 表示当前位于点 \(i\) 的最短路,每个点只能由上一列的两个点转移而来。分别以 \(n-1,2n\) 作为起点 dp 即可。
关于判断负环,其实不需要真的把图建出来。根据前面的性质,负环要么经过点 \(n\),要么经过 \(0\) 到 \(2n\) 的边。得到 \(2n\rightarrow 0\),\(n-1\rightarrow n+1\),\(n-1\rightarrow 0\),\(2n\rightarrow n+1\) 的最短路之后,只需要判断存不存在 \(2n\rightarrow 0\),\(2n\rightarrow n\),\(n-1\rightarrow n+1\rightarrow n\),\(n-1\rightarrow 0\rightarrow n\) 这四种负环即可。
时间复杂度 \(\mathcal{O}(n\log A_i)\)。
ARC118
[ARC118A] Tax Included Price
不难想到枚举 \(A\) 模 \(100\) 的余数 \(r\),那么 \(A\) 与 \(A+100\) 算出来的差为 \(100+t\),是一个整数。也就是说,这个东西是有周期性的。
考虑打个表,把所有不能取到的位置找出来,算出周期 \(T\)。只需要看 \(N\) 跨越了几个整周期以及余数即可。
时间复杂度 \(\mathcal{O}(1)\)。
[ARC118B] Village of M People
不难想到二分答案,只需要检查 \(\left|\dfrac{b_i}{m}-\dfrac{a_i}{n}\right| \leq x\)。但是实数域二分太掉精度,于是我们通分一下得到 \(|b_in-a_im|\leq X\),转而去二分这个 \(X\)。
可以得到 \(\dfrac{-X+a_im}{n}\leq b_i \leq \dfrac{X+a_im}{n}\),两边分别上下取整,可以得到 \(b_i \in [L_i,R_i]\)。
现在的问题转为,对于有范围限制的 \(b_i\) 给出一组总和为 \(m\) 的构造。这个是容易的,我们先全都调到下界,再试图往上调,直到调整至总和为 \(m\) 即可。
时间复杂度 \(\mathcal{O}(k \log nm)\)。
[ARC118C] Coprime Set
容易想到用 \(2,3,5\) 去构造。直接取 \(6,10,15\) 的倍数,排序后取前 \(n\) 小即可。
注意一些细节,要从 \((16,+\infty)\) 开始选,否则小数据会出问题。
时间复杂度 \(\mathcal{O}(n+V)\)。
[ARC118D] Hamiltonian Cycle
把路径看作在一张二维网格图上游走,上下移动看作乘上或除以一个 \(a\),左右移动看作乘上或除以一个 \(b\),则原问题等价于找一条经过 \(p\) 个点的回路。
加强一下,变成 \(n\times m\) 的网格图。要求 \(n \times m=p-1\)。不妨取 \(n=\delta_p(a)\),记集合 \(S=\{a^i \bmod p\}\),那么我们取 \(m\) 为最小的使得 \(b^m \in S\) 的正整数。
为什么这么取?因为 \(m\) 意味着向右走 \(m\) 次就走到了和第一列本质相同的一列,后面的就都可以不管了。如果前面 \(n\times m\) 的网格满足不了,保留后面的也满足不了。
对于这个网格,\((i,j)\) 上填入 \(a^ib^j \bmod p\),并且 \(n \times m=p-1\)。对于 \(p=2\) 的情况,只需要走一行。对于 \(p\) 取其他素数的情况,\(n,m\) 中一定有一个偶数,那么哈密顿回路是容易构造出来的。
时间复杂度 \(\mathcal{O}(p)\)。
[ARC118E] Avoid Permutations
ARC140
[ARC140A] Right String
注意到,答案等价于字符串的最小整周期。
暴力枚举 \(d \mid n\),对于对位的 \(i,i+d,i+2d,\cdots\) 这些位置上找到出现次数最多的字符,把其他字符全都换成这个字符一定是操作次数最小的。如果这些修改次数之和 \(\leq k\) 就对了。
时间复杂度 \(\mathcal{O}(n\sqrt{n}+n|\Sigma|)\)。
[ARC140B] Shorten ARC
考察每一个形如 \(\texttt{AA}\cdots\texttt{AARCC}\cdots\texttt{CC}\) 的结构,一次操作一相当于缩短这个串,而一次操作二相当于直接废掉了这个串,因为在 \(\texttt{R}\) 右边的 \(\texttt{A}\) 和左边的 \(\texttt{C}\) 都是没用的。
把每一个这样结构的串都拿出来,记一共有 \(cnt\) 个,那么这些串至多在 \(2\times cnt\) 轮就全都被废掉了。同时每个串至多被执行 \(\min(A,C)\) 次操作一,记操作次数总和为 \(S\)。答案就是 \(\min(2\times cnt,S)\)。
时间复杂度 \(\mathcal{O}(n)\)。
[ARC140C] ABS Permutation (LIS ver.)
直观感受,最优的构造应该是一个上下跳跃的样子。当 \(X\) 恰好在 \(N\) 一半的时候,可以取到上界 \(N-1\)。
对于其他情况,构造不出 \(N-1\) 来了。于是我们考虑牺牲一次机会,换得 \(N-2\) 的构造。具体来说,取剩下的数的中位数,把它放在第二个位置,其他的数继续上下跳跃。这样 \(b_1=|a_2-a_1|\) 会被浪费掉,但是后面的仍然递增,并且 \(N-2\) 已经是顶满的上界了,自然是对的。
时间复杂度 \(\mathcal{O}(n)\)。
[ARC140D] One to One
每个连通块都是基环树森林,从而我们可以将统计连通块转化为统计环。
先不考虑 \(a_i=-1\) 的连边,用并查集维护确定的边,那么此时每个连通块一定都是树或者基环树。同时对于每个是树的连通块,里面一定恰好有一个点的 \(a_i=-1\)。
考虑计算每个环在多少种方案中出现过,这样它就做了多少次贡献。
我们只关心环的贡献,此时树接基环树是不会有影响的,只有树之间连接才会产生新的环。设一共有 \(m\) 棵树,则一个基环树的贡献就是 \(n^{m}\),可以先不管。
对于是树的连通块,考虑用 \(k\) 棵树串成一棵基环树,统计这个环的贡献。那么 \(k\) 的答案就是在 \(m\) 个 \(|V_i|\) 中选择 \(k\) 个数的乘积的和。这个东西是一个 dp 可以解决的,先放着。
但是我们只是选出来了 \(k\) 棵树串起来,还要钦定它们之间的顺序,这个东西就是圆排列,可以知道有 \((k-1)!\) 种方法。同时,其他 \(m-k\) 棵树可以任意连,方案数为 \(n^{m-k}\)。
考虑上面那个 dp,不难想到设 \(f(i,j)\) 表示前 \(i\) 个数选了 \(j\) 个的乘积之和,转移是容易的。
\[f(i,j)=f(i-1,j-1)\times |V_i|+f(i-1,j) \]这部分最后的答案就是:
\[\sum_{i=1}^m f(m,i)\times (i-1)!\times n^{m-i} \]时间复杂度 \(\mathcal{O}(n^2)\)。
[ARC140E] Not Equal Rectangle
神秘构造。感觉这辈子也做不出来。后文中下标以 \(0\) 开始。
取 \(p=23\),将表格加强成 \(p^2 \times p^2\),考虑填一个合法的 \(p\times p\) 的子表格 \(B\),通过将这个子表格进行调整得到合法的完整表格。
考虑一个经典的轮换构造,\(B_{i,j}=(i+j) \bmod p\)。这样子表格内不会出问题。直接将其复制 \(p^2\) 份显然是不成立的,将第 \(i\) 行第 \(j\) 列的子表格中的每个数加上 \((i\times j) \bmod p\) 即可。我们称「加上 \(x\) 之后的子表格」为 「\(x\) 类子表格」,那么也就是在第 \(i\) 行第 \(j\) 列的子表格放上了 \((i\times j) \bmod p\) 类子表格。
接下来证明这个东西是成立的。考虑反证,假设存在四个位置相等,不妨设它们是顺时针的,且分别在 \(a,b,c,d\) 四类子表格内,则有 \(|a-b|=|c-d|\)。这个式子意味着 \(a,d\) 在同一个子表格内,从而会导致矛盾。
时间复杂度 \(\mathcal{O}(nm)\)。
标签:选做,记录,复杂度,times,ARC,提交,mathcal,sum From: https://www.cnblogs.com/duckqwq/p/18132132